
Machines à calculer
Cette « exposition virtuelle » a pour objectif la mise en valeur du patrimoine de l’Amisa. Elle propose, quand cela est possible, des explications sur le fonctionnement des machines présentées (modes d’emploi, séquences vidéo, simulations…).
Un jeu de six familles
Une façon de présenter les objets pourrait être de les regrouper en six grandes catégories, énumérées ci-dessous.
1. Les systèmes qui reposent sur la manipulation plutôt que sur une numération écrite
La première façon de calculer, la plus naturelle, utilise les dix doigts de la main ; c’est probablement là l’origine du système décimal.
Au-delà des doigts, la mémoire des nombres a été conservée sous la forme de petits cailloux (calculi en latin, d’où le terme calcul), de nœuds sur des ficelles multicolores (le quipu des incas), ou encore sous forme d’entailles pratiquées dans un morceau de bois. Les petits cailloux ont aussi été remplacés par des jetons, plus faciles à manipuler lors des calculs.
Amisa (Collection IBM-Europe)
Ensemble lié de cordelettes dont les matières, les couleurs, les longueurs, les formes des nœuds et leurs positions correspondent à un système de consignation de données, utilisé dans le système de comptabilité de l’administration inca.
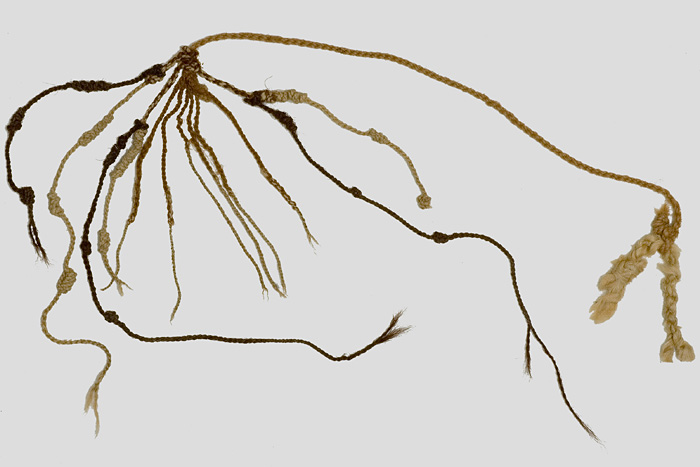
© Inria / Photo J.-M. Ramès
D’après Gary Urton, professeur d’anthropologie à l’université de Harvard :
« Les quipus peuvent se résumer en une succession de décisions à double choix. Les cordes sont en coton ou bien en laine. Quand on débute un nœud, on peut faire glisser la corde vers la droite ou bien vers la gauche, puis continuer vers le haut ou vers le bas, etc. En tout, j’ai dénombré sept étapes qui autorisent chacune deux décisions. Je pense que des informations se cachent derrière ce système, suivant le même principe que l’informatique. »


À l’heure actuelle, les quipus ne sont pas déchiffrés.
Pour en savoir plus : The Khipu Database Project, Université de Harvard (en anglais).
L’idée de fixer les jetons dans des glissières permit de construire des abaques portables et les premiers bouliers. Le boulier eut un succès considérable en Asie et en Europe centrale : suanpan chinois, soroban japonais et stchoty russe.
13 x 8 cm – 120 g – Amisa (Collection IBM-Europe)
Depuis longtemps, l’homme a appris à mener des calculs en déplaçant des cailloux sur un abaque de sable, de pierre ou de bois (le nom latin pour caillou est calculus – étymologie du mot calcul).
Sur cet abaque portable, en ivoire, les cailloux sont remplacés par de petites boules qui coulissent dans des rainures.

© Inria / Photo J.-M. Ramès
Chaque colonne (de la première à la huitième) représente une puissance de 10 :
- la rainure du bas comporte quatre boules unitaires,
- la rainure supérieure comporte une boule, représentant cinq unités.
Un nombre se lit avec les boules se trouvant proches de la transversale. Les opérations se font par déplacement des boules. Pour en savoir plus sur le fonctionnement des bouliers, voir le Wikibook : S’initier au boulier en 10 leçons.
Les fractions se calculent dans le système duodécimal, par onces (douzièmes de l’as) et par fractions d’once.
La neuvième colonne, marquée du signe ![]() (once), a cinq boules inférieures valant une once et une boule supérieure qui en vaut six : on peut ainsi compter jusqu’à 11.
(once), a cinq boules inférieures valant une once et une boule supérieure qui en vaut six : on peut ainsi compter jusqu’à 11.
La dixième colonne comprend trois petites rainures correspondant à :
 1/2 once (1 boule),
1/2 once (1 boule), 1/4 once (1 boule),
1/4 once (1 boule), 1/3 once (2 boules).
1/3 once (2 boules).
2. Les systèmes basés sur la numération écrite et les tables de multiplication
Au XVIIe siècle, John Neper (ou Napier), mathématicien écossais, mit au point des bâtons mobiles qui permettent de réaliser rapidement des multiplications, grâce à une représentation astucieuse des tables de multiplications.
14 x 10 cm – 320 g – Amisa (Collection IBM-Europe)
Inventés vers 1600 par le mathématicien écossais John Neper (ou Napier), à partir d’un ancien procédé appelé « per gelosia », ces bâtons représentent en fait une disposition spéciale de la table de multiplication qui facilite et accélère les opérations coutumières. À l’origine, ils sont quadrangulaires, numérotés de 0 à 9, et porteurs des 9 premiers multiples de leur chiffre numérique. Ces résultats sont inscrits sur des carrés superposés, divisés en 2 par un trait diagonal séparant pour chaque produit les unités des dizaines.

© Inria / Photo J.-M. Ramès
Utilisation des bâtons de Neper
Visionner la séquence vidéo réalisée par Caroline Chanvin – Durée : 1 min 33 s.
Simulation de l’utilisation des bâtons de Neper
Cette animation Flash a été réalisée par tan-gram.
- Pour définir les trois chiffres du multiplicateur, choisir la valeur, entre 0 et 9, de chacun des trois bâtons en utilisant les flèches – et + situées sous chaque bâton.
- Pour choisir le multiplicande, déplacer le curseur le long de la colonne de gauche.
- Le résultat s’affiche dans la partie droite de l’écran, avec sa décomposition en quatre zones colorées : bleu (les milliers), gris clair (les centaines), gris foncé (les dizaines) et rouge (les unités).
Présentation des bâtons de Neper dans l’Encyclopédie de Diderot et D’Alembert (tome 22) :


Pour en savoir vraiment plus, vous pouvez télécharger le traité de Neper Rabdologiae seu numerationis per virgulas libri duo (fichier pdf – 116 Mo – en latin !).
Des variantes, utilisant par exemple des feuillets cartonnés, ou associant différents systèmes seront créés et utilisés jusqu’à la fin du XIXe siècle.
10 x 13 cm – 120 g – Amisa (Collection IBM-Europe)
Lamelles en carton imprimées sur les 2 faces.
Les feuillets sont basés sur le même principe que les bâtons népériens. Les lamelles sont déplaçables. Pour effectuer une multiplication, on range les lamelles correspondant aux chiffres du multiplicateur à côté de la lamelle du multiplicande (chiffres romains) dans leur ordre successif. Le produit (par exemple V multiplié par 456) est obtenu en prenant les carrés de la ligne multiplicande (ligne V, carrés marqués 2/0, 2/5, 3/0) et en ajoutant les chiffres qui sont dans une même bande diagonale (2 et rien donnent 2 pour le premier carré, 0 et 2 donnent 2 pour la bande 1er et 2e carré, 5 et 3 donnent 8 pour la bande 2e et 3e carré, 0 et rien donnent 0 pour le 4e carré) ; le produit est donc 2280.

© Inria / Photo J.-M. Ramès
12 x1 8 cm – 220 g – Amisa (Collection IBM-Europe)
Il associe 8 cylindres népériens à un boulier doublé de petits tambours numérotés mémorisant les additions.

© Inria / Photo J.-M. Ramès
3. Les règles à calcul, basées sur les logarithmes
Le logarithme d’un produit est égal à la somme des logarithmes de chaque facteur du produit. Une règle, graduée en échelle logarithmique, permet donc de transformer des multiplications en additions et des divisions en soustractions.
L’ancêtre de la règle à calcul est la règle logarithmique proposée en 1624 par Edmund Gunter (1581-1626). Celui-ci y avait reporté des segments de longueur proportionnelle aux logarithmes des nombres ; les multiplications et divisions se faisaient à l’aide d’un compas. William Oughtred (1574-1660) proposa vers 1630 de reporter la même échelle sur deux règles disposées l’une à côté de l’autre. La réglette centrale coulissante, qui fut utilisée sur la plupart des règles jusqu’aux environs de 1970, fut imaginée en 1657 par Seth Patridge.
De nombreuses règles à calcul furent fabriquées pour des usages spéciaux, telle la règle de Routledge ou la règle de Hawthorn.
32 x 4 cm – 100 g – Amisa (Collection IBM-Europe)
Le concept de cette règle a été décrit par Henry Coggeshall dès 1677 dans « Timber Measure by a Line of more Ease, Dispatch and Exactness than any other way now in use, by a Double Scale. . . . », puis plus précisément en 1722 dans « The Art of Practical Measuring easily performed by a Two-foot Rule which slides to a Foot ».
Ce concept a servi de base à Joshua Routledge (1773 – 1829) de Bolton, en Angleterre, pour le développement d’une règle à calcul destinée aux ingénieurs.
Le modèle présenté ici a été fabriqué dans les ateliers Sampson Aston à Birmingham.

© Inria / Photo J.-M. Ramès
Les échelles A (fixe), B et C (mobiles) comportent deux cycles de logarithmes.
L’échelle D a un cycle de logarithmes et va de 4 à 40. Elle est appelée la « girt line » (girt = 1/4 de la circonférence d’un tronc d’arbre).

La règle peut être utilisée pour calculer le volume d’un tronc d’arbre. Il est nécessaire d’avoir la longueur de l’arbre en pieds, et le « girt » exprimé en pouces, c’est-à-dire le quart de la circonférence du tronc (mesuré en utilisant une corde que l’on plie deux fois). On fait coïncider la longueur en pieds sur l’échelle C avec le 12 sur l’échelle D (la « girt line »). Face au « girt » exprimé en pouces sur la ligne D, on a le volume en pieds 3 sur l’échelle C. En fait, la valeur trouvée est seulement d’environ 80 % (π/4) du volume théorique, pour tenir compte des pertes lorsque l’arbre sera débité en planches.

Trois repères correspondent à des unités de volume :
- AG – Ale gauge – 18,95 l
- WG – Wine gauge – 17,15 l
- IG – Imperial gallon – 18,8 l
La règle comporte une table monétaire, avec une colonne exprimée en pence (D – denarius), et une colonne exprimée en livres (L – Libra), shillings (S – solidus) et pence (D – denarius). Une livre était divisée en 20 shillings chacun divisé en 12 pences. La valeur en livres, shillings et pence correspond à 50 fois la valeur de la colonne en pence. Par exemple, 14 pences correspondent à 2 livres, 18 shillings et 4 pences, c’est-à-dire 700 pences. Ce facteur multiplicateur correspond à une charge de bois égale à 50 pieds 3.

32 x 5 cm – 80 g – Amisa (Collection IBM-Europe)
Règle pliante avec réglette mobile et diverses échelles, « Improved and arranged by Robert Hawthorn, Civil Engineer, Newcastle-upon-Tyne ».

© Inria / Photo J.-M. Ramès
Cette règle comporte une table de mesures. En colonnes :
- parallélépipèdes
- FFF : toutes les dimensions sont en pieds (feet)
- FFI : la longueur est en pieds, les autres dimensions en pouces (inches)
- III : toutes les dimensions sont en pouces
- cylindres
- FI : la longueur est en pieds, le diamètre en pouces
- II : toutes les dimensions sont en pouces
- sphères
- F : le diamètre en pieds
- I : le diamètre en pouces
En lignes :
- les volumes en pieds et en pouces
- les volumes « imperial gallon » et « water »
- les données pour divers matériaux
D’autres données concernent en particulier les machines à vapeur.
Pour en savoir plus : le mode d’emploi original, en anglais.
Pour accroître la précision, M. Péraux de Nancy imagina une règle à deux réglettes.
L’utilisation des graduations logarithmiques donna aussi naissance à des cercles de calcul, tels que l’arithmographe Gattey ou le cercle à calcul Blitz.
28 x 4,5 cm – 180 g – Amisa (Collection IBM-Europe)
Il s’agit de cinq réglettes horizontales solidaires, dont deux sont coulissantes. L’idée de Péraux, commerçant à Nancy, était d’accroître la précision de la règle sans en augmenter la longueur.

© Inria / Photo J.-M. Ramès
diamètre 15 cm – 120 g – Amisa (Collection IBM-Europe)
Le décret relatif aux poids et aux mesures du 18 germinal an 3 (7 avril 1795), stipule que « les citoyens sont invités de donner une preuve de leur attachement à l’unité et à l’indivisibilité de la République en se servant dès à présent des nouvelles mesures dans leurs calculs et transactions commerciales ». Il précise en son article 19 que « Au lieu des tables des rapports entre les anciennes et les nouvelles mesures, il sera fait des échelles graphiques pour estimer ces rapports sans avoir besoin d’aucun calcul ».
C’est dans ce contexte que François Gattey (1756 – 1819) proposa l’usage de cadrans logarithmiques qu’il renomma en 1810 « arithmographes ».

© Inria / Photo J.-M. Ramès
- 1799 Instructions sur l’Usage des Cadrans logarithmiques – François Gattey (Paris)
- 1810 Explication et usage de l’arithmographe – François Gattey (Paris), réédité en 1819 sous le titre Usage du calculateur, instrument portatif au moyen duquel on peut en un instant, et sans être obligé d’écrire aucun chiffre, se procurer les résultats de toutes sortes de calcul.
diamètre 18,5 cm – 80 g – Amisa (Collection IBM-Europe)
Cercle logarithmique dérivé de la règle à calcul.
Cet appareil a été inventé par Julius Billeter (1828 – 1914) de Zurich.

© Inria / Photo J.-M. Ramès
4. Les additionneurs mécaniques
La machine arithmétique de Caze et le totalisateur Troncet n’incluent pas le report des retenues.
L’additionneuse Lapeyre, en bois, comporte des engrenages rudimentaires.
L’additionneur de Webb est un lointain descendant de la machine de Pascal.
L’arithmographe Clabor et l’arithmographe Trick permettent la prise en compte mécanique des retenues.
27 x 17 cm – 80 g – Amisa (Collection IBM-Europe)
Cette machine est dérivée du boulier. Les réglettes coulissantes sont graduées de 1 à 9 de haut en bas. Elles se manœuvrent à l’aide d’un piquoir. Cette machine n’inclut pas le report des retenues.

© Inria / Photo J.-M. Ramès
18 x 25 cm – 480 g – Amisa (Collection IBM-Europe)
Deux roues dentées mobiles à l’intérieur de deux cercles fixes numérotés de 0 à 495 pour les Francs, et de 0 à 99 pour les centimes.

© Inria / Photo J.-M. Ramès
Mode d’emploi du Totalisateur Troncet pour les nombres entiers et les monnaies


20 x 25 x 5 cm – 1640 g – Amisa (Collection IBM-Europe)
Un disque mobile, dont le bord est divisé en 100 segments, est déplaçable par rotation devant une graduation fixe et permet la sommation de deux chiffres. Deux autres disques mobiles permettent de comptabiliser les centaines et les milliers.

© Inria / Photo J.-M. Ramès
11 x 6 cm – 400 g – Amisa (Collection IBM-Europe)
Additionneur circulaire composé de deux cercles tangents, dont l’un correspond aux 99 premières unités, l’autre aux centaines. Il est manœuvré par un stylet et permet les additions jusqu’à un total de 4999. Le total apparaît dans une lucarne percée au point de rencontre des deux cercles. Cet additionneur est un lointain descendant de la machine de Pascal.

© Inria / Photo J.-M. Ramès
Cet additionneur a été inventé par l’écrivain américain Charles Henry Webb (1834 – 1905). Le brevet (en anglais), déposé le 12 décembre 1889, décrit de façon détaillée le fonctionnement de l’appareil.
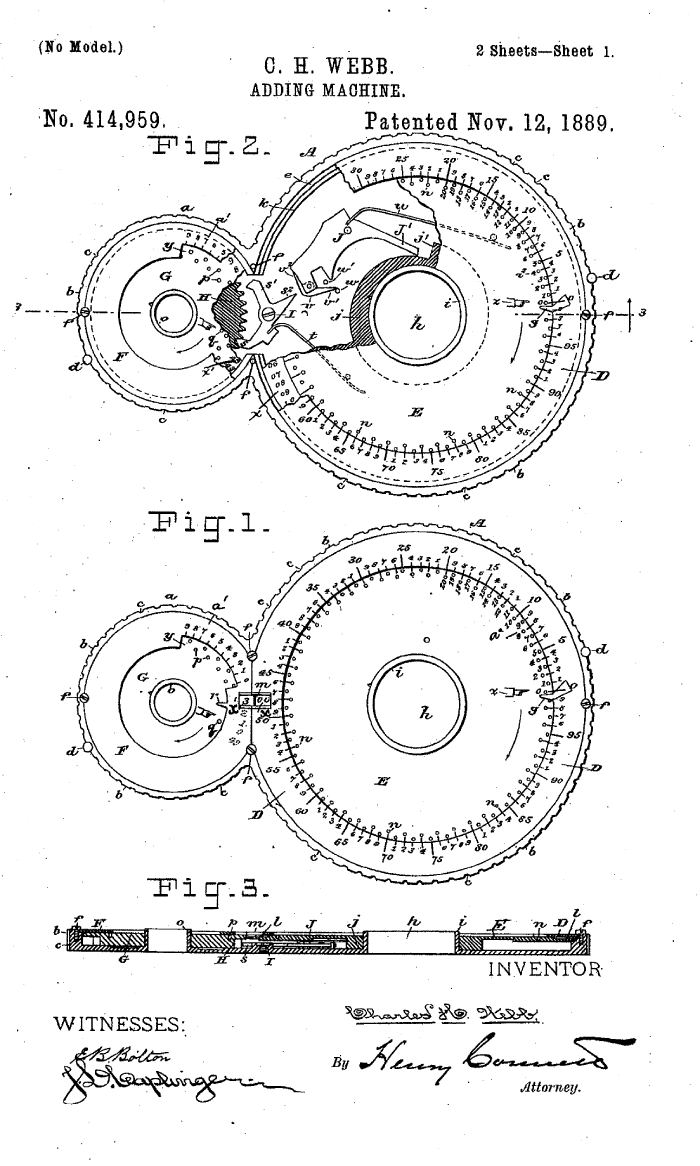
37 x 5 cm – 380 g – Amisa(Collection IBM-Europe)

© Inria / Photo J.-M. Ramès


16 x 9 cm – 340 g – Amisa (Collection -Europe)
Machine à huit chiffres décimaux.
Utilisation de l’arithmographe
Visionner la séquence vidéo réalisée par Caroline Chanvin – Durée : 1 min 57 s.
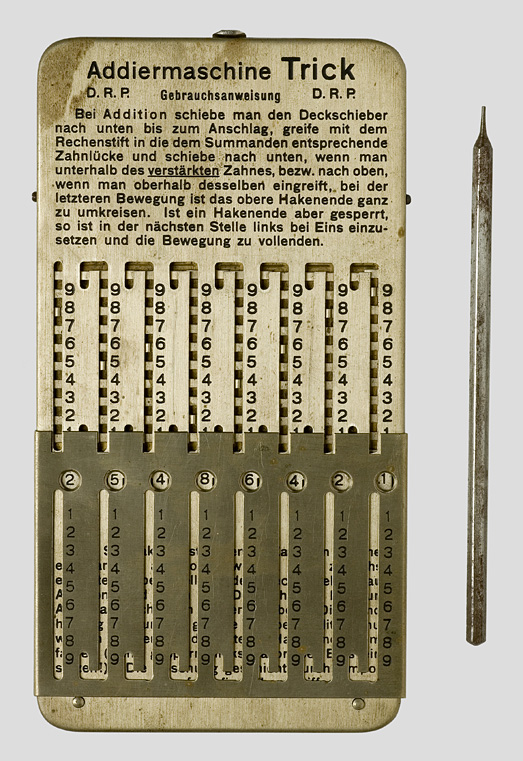
© Inria / Photo J.-M. Ramès

5. Les multiplicateurs mécaniques
En plus des additions et des soustractions, l’arithmographe de Léon Bollée est doté d’un ensemble de réglettes métalliques permettant de faire les multiplications et les divisions.
31 x 29 x 5 cm – 3540 g – Amisa (Collection IBM-Europe)
Il comprend un additionneur à crosses et une série de réglettes de Genaille disposées en feuillets superposés permettant l’exécution des multiplications et de divisions.

© Inria / Photo J.-M. Ramès
Utilisation de l’arithmographe
Visionner la séquence vidéo réalisée par Caroline Chanvin – Durée : 4 min 21 s.
« Cet appareil est constitué par la réunion de deux parties principales : l’une destinée à opérer les additions et soustractions, et l’autre, dont l’emploi se combine avec celui de la première quand il s’agit d’effectuer les multiplications et les divisions.

La première partie forme une sorte de tableau métallique percé de lumières allongées et d’ouvertures rondes en-dessous desquelles coulissent des réglettes additives et soustractives disposées de façon à donner, par de simples mouvements de déplacement des réglettes, les résultats de l’addition et de la soustraction d’unités successives, avec report des retenues, quand il y a lieu, d’une réglette à la suivante.
Ces résultats apparaissent dans les ouvertures rondes de l’appareil, et les déplacements des réglettes s’opèrent à l’aide d’un poinçon que l’on introduit dans les trous que porte la partie supérieure, et qui se présentent en regard de chiffres gravés le long des lumières allongées.
Deux règles de manœuvre placées à la partie inférieure permettent de remettre rapidement toutes les réglettes au zéro.
…
M. Léon Bollée a réalisé un grand perfectionnement par l’addition de la seconde partie de l’appareil, qui est constituée par un châssis mobile portant des séries de réglettes que l’on peut amener en regard des précédentes, et qui donne l’indication immédiate des produits partiels qui entrent dans les opérations en évitant d’avoir à former ces produits par additions successives.

Ce châssis porte six groupes composés chacun de neuf réglettes, en forme de feuillets superposés en paquets et montées à charnière de façon à pouvoir se relever individuellement. Ces réglettes sont numérotées de 1 à 9, et portent en regard des divisions des fenêtres, des chiffres qui indiquent les déplacements à opérer pour chaque chiffre multiplicateur employé.
Après avoir fait marquer aux réglettes du châssis le multiplicande, on obtient le produit de ce nombre par les unités du multiplicateur en effectuant simplement les déplacements des réglettes indiquées sur chaque feuillet par le chiffre des unités. On obtient de même le produit par le nombre formé des deux premiers chiffres du multiplicateur en déplaçant le châssis d’un cran vers la gauche, et opérant pour le chiffre des dizaines comme on a fait pour celui des unités. On opérera de la même façon pour le chiffre des centaines, etc., en transportant successivement les châssis vers la gauche.
L’appareil construit par M. Léon Bollée, dont le châssis porte 6 paquets de réglettes, peut donner des produits de quatorze chiffres, et se prêter à toutes les combinaisons arithmétiques que permettent les machines à calculer. Il est portatif et peu encombrant, de construction solide et soignée et d’un usage commode.
Il abrège considérablement les calculs, en supprimant tout travail intellectuel. »
Extrait du rapport fait par le général Sebert sur les machines à calculer de M. Léon Bollée (1895).
Remerciements à Michel Mouyssinat pour les documents sur l’arithmographe de Léon Bollée.
6. Les machines électromécaniques
Les calculs statistiques nécessaires à l’activité économique sont traités à l’aide de trieuses de cartes perforées, inventées en 1890 par l’américain Hollerith pour traiter les masses de données issues des recensements de population.
Amisa (Collection IBM-Corbeil)

(Archives IBM)
Répondant à un concours lancé par le gouvernement américain pour accélérer le dépouillement des recensements, Herman Hollerith imagina et construisit la première machine à statistiques.
Le principe de fonctionnement est assez simple. L’opérateur met une carte dans la machine, et fait descendre une presse, couverte de tiges munies de ressorts. Lorsqu’une tige est face à un trou, elle traverse la carte et vient baigner dans une petite dose de mercure, ce qui ferme un circuit électrique. Ce circuit incrémente un des compteurs de la machine, et provoque l’ouverture d’un des 24 conteneurs, où l’opérateur dépose la carte.
Mise au point pour effectuer le recensement américain de 1890, cette machine qui utilise des cartes perforées a fait le succès de la « Tabulating Machine Company » devenue plus tard « IBM ».

Compteurs électromagnétiques
© Inria / Photo J.-M. Ramès

Trieuse de cartes perforées
© Inria / Photo J.-M. Ramès
Ce document ne prétend pas retracer une histoire complète des machines à calculer. Manquent en particulier la machine de Pascal, ou Pascaline, et celle de Leibniz, dont l’Amisa ne possède pas d’exemplaire. Pour en savoir plus, on pourra par exemple lire le texte de Jean Vuillemin Les langages numériques (fichier pdf – 3,8 Mo) paru dans Mécanique des signes et langages des sciences Grenoble, CNRS-MSH-Alpes, janvier 2003. À voir aussi, le site Linealis.org consacré aux instruments de calcul. À lire, en anglais, le livre de Florian Cajori History of the logarithmic slide rule (fichier pdf – 5,7 Mo), Colorado Springs, 1909.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Moncef Mlouka
Directeur de recherche Inria et secrétaire de l'Amisa, Association pour le musée international du calcul, de l'informatique et de l'automatique de Valbonne Sophia Antipolis.
