
La combinatoire des Sudokus
C'est par sa nature combinatoire : il y a un grand nombre de combinaisons possibles, et que ce soit dans le but de résoudre ou de générer une grille, il s'agit de trouver celle qui correspond à certains critères.
Cependant, les problèmes combinatoires ne sont pas toujours ludiques. Définir un emploi du temps pour les équipes d’infirmières d’un hôpital, organiser les tournées d’une équipe de livreurs, planifier un chantier… quel est le point commun entre tous ces problèmes a priori différents ? C’est leur nature combinatoire ! Là aussi, y a un grand nombre de combinaisons possibles, et il s’agit de trouver la meilleure d’entre elles selon un certain critère : temps, coût…
Problèmes combinatoires et techniques de résolution
Ces problèmes sont des problèmes discrets, car ils portent sur des variables entières. Contrairement à ce que pourrait laisser penser l’intuition, ces problèmes sont souvent plus difficiles à résoudre que les problèmes continus, portant sur des variables réelles. En effet, alors que la dérivation des fonctions est un outil puissant permettant d’aborder les problèmes d’optimisation continus, on manque cruellement d’outils mathématiques pour la résolution des problèmes discrets.
Il existe toutefois certaines techniques informatiques, programmation linéaire, programmation dynamique et programmation par contraintes (en abrégé PPC), qui permettent de résoudre ces problèmes sur ordinateur.
C’est pourquoi des liens étroits peuvent être montrés entre la programmation par contraintes et le problème combinatoire à la mode qu’est le Sudoku.
Sudokus et autres jeux
Depuis l’année 2005, de petites grilles de 9×9 cases envahissent le web et les journaux. Il s’agit du Sudoku. Ce jeu, inventé aux États-Unis en 1979, à partir du principe du carré latin, a été popularisé au Japon depuis 1986 et a alors pris un nom japonais.
Une des raisons de son succès est sa simplicité. Il peut en effet être décrit par une seule règle : chaque ligne, colonne et carré de 3×3 doit contenir tous les chiffres de 1 à 9.
Voici un exemple jouable, de niveau facile.
Alors que le Sudoku original est une grille 9×9, il existe désormais de nombreuses variantes : Sudoku 4×4 pour les enfants, Monster Sudoku (16×16) pour les accros, Killer Sudoku où les grilles sont pavées par des zones associées à des sommes…
Un autre jeu a déjà détrôné le Sudoku au Japon, il s’agit du Kakuro, sorte de mots croisés numériques faisant aussi intervenir des sommes. Ce jeu peut également être résolu et généré avec des techniques de programmation par contraintes.
Techniques de résolution des Sudokus
Si le Sudoku passionne le grand public, c’est parce que chacun peut s’inventer ses propres techniques de résolution. Or ces techniques rejoignent celles mises en œuvre par les informaticiens dans le cadre de la programmation par contraintes.
On peut grossièrement classer ces techniques en deux catégories :
- celles qui cherchent à placer une valeur dans une ligne, colonne ou sous-carré,
- celles qui cherchent à trouver la valeur correspondant à une case donnée.
En partant du Sudoku donné au début du document, on peut placer la valeur 9 dans le carré en bas à gauche. En effet, la valeur 9 ne peut être ni dans la première colonne, ni dans la dernière ligne. Elle n’a donc plus qu’une place possible dans le carré.
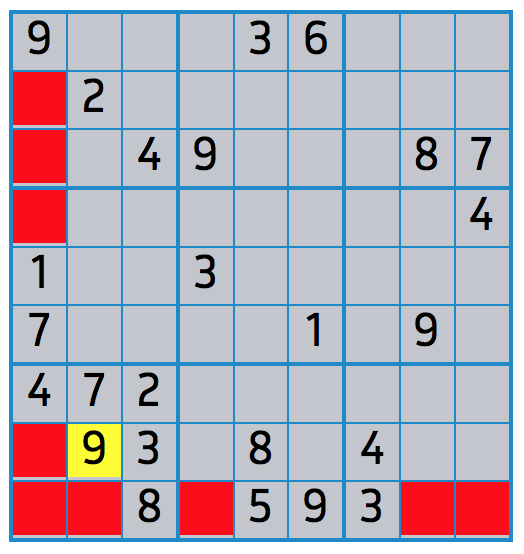
En partant du Sudoku donné au début du document, on peut trouver la valeur qui est sur la 7e ligne et la 6e colonne. En effet,
- sur la ligne horizontale qui passe par cette case, il y a les valeurs 4, 7 et 2 ;
- sur la ligne verticale qui passe par cette case, il y a les valeurs 6, 1 et 9 ;
- dans le carré qui contient cette case, il y a les valeurs 8, 5 et 9 ;
soit au total 8 valeurs différentes : donc, seule la valeur 3 peut convenir.
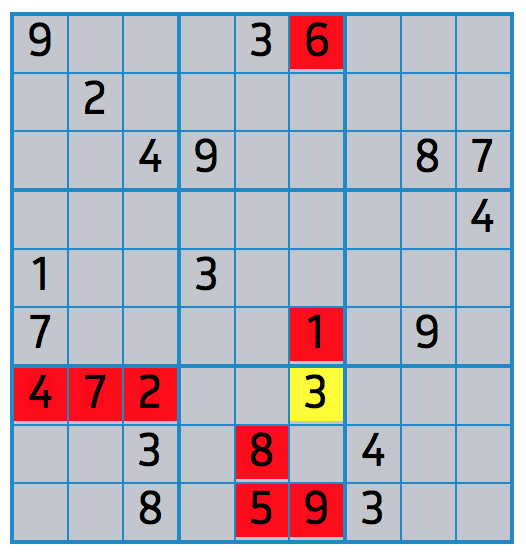
Pour les Sudokus difficiles, les joueurs sont souvent amenés à raffiner la deuxième technique, en considérant les ensembles de valeurs qui sont candidates pour une case donnée. Ces raisonnements sur des ensembles de valeurs sont identiques à ceux qui sont faits automatiquement par les résolveurs de contraintes et sont appelés filtrage ou bien maintien de la consistance par les spécialistes de la programmation par contraintes.
Enfin, pour les Sudokus de niveau expert, on est parfois amené à faire des hypothèses. Cette dernière technique est aussi classique dans la programmation par contraintes, du fait de la nature exponentielle des problèmes abordés.
La résolution de Sudokus est un cas d’école pour la programmation par contraintes. Un article du même auteur publié sur java.net (en anglais) expliquait en détail comment modéliser le problème des Sudokus en programmation par contraintes. Une traduction de cet article en français a été publiée par la revue La Recherche dans la rubrique Wxyz, n° 395 de mars 2006 (version en ligne, réservée aux abonnés). La bibliothèque de PPC utilisée dans cet article est Koalog Constraint Solver, écrite en Java, mais la modélisation n’est pas dépendante du choix du logiciel.
La résolution d’un Sudoku se fait en quelques millisecondes sur un PC de bureau.
Mise à part la résolution, d’autres problèmes sont à considérer : génération et calcul des niveaux, dont nous verrons qu’ils sont étroitement liés aux techniques de résolution.
Génération des Sudokus
Si la génération manuelle de Sudokus a encore ses adeptes (principalement au Japon), la plupart des grilles sont désormais générées par ordinateur.
Rappelons que l’objectif à atteindre est de générer une grille partiellement remplie conduisant à une unique solution. On dit que le Sudoku est bien formé. Une propriété supplémentaire est la minimalité des indications. Plus précisement, chaque indication doit être indispensable : si on la supprimait, alors le Sudoku n’aurait plus une solution unique. On dit que le Sudoku est localement minimal.
Un schéma d’algorithme pour générer un Sudoku bien formé et localement minimal est le suivant :
- on génère une grille aléatoirement
- on initialise une liste de cases à effacer avec toutes les cases du Sudoku
- on choisit au hasard une case dans cette liste (et on l’enlève de la liste)
- on efface, dans la grille, la valeur dans cette case
- si le Sudoku n’a pas une solution unique, alors on remet la valeur effacée
- si la liste est non vide, on va en 3, sinon on a terminé
Cet algorithme suppose que l’on sait résoudre n’importe quel Sudoku… ce qui est vrai grâce à la programmation par contraintes. À l’étape 1, pour générer une grille de façon aléatoire, il suffit d’appliquer une technique de résolution sur une grille vide, sans aucune donnée initiale. De même, à l’étape 5, il suffit de chercher deux solutions au Sudoku pour montrer que la solution n’est pas unique.
Par ailleurs, l’étape 3 enlève une case de la liste, de ce fait la longueur de la liste décroît strictement à chaque itération, et la liste va donc finir par être vide : ceci garantit que l’algorithme termine.
Calcul des niveaux
Le calcul des niveaux se révèle la partie la plus délicate. La difficulté doit en effet correspondre à celle qui est attendue par les joueurs pour le niveau annoncé, c’est un facteur primordial pour la satisfaction des joueurs. Ce point fait l’essentiel de la différence entre les producteurs de Sudokus concurrents.
Une technique (celle utilisée par la société Koalog pour noter ses Sudokus en six niveaux) consiste à définir un ensemble de règles de résolution de difficulté croissante, et à noter les Sudokus en fonction de la difficulté des règles nécessaires pour la résolution.
Par exemple, on peut considérer que la règle placement d’une valeur dans un carré est plus simple que la règle détermination de la valeur dans une case donnée. Les Sudokus qui peuvent être résolus uniquement à l’aide de la première de ces deux règles seront donc considérés comme plus simples que ceux qui nécessitent d’utiliser les deux règles.
Ainsi donc, les liens qui existent entre le Sudoku et les techniques de programmation par contraintes sont mis en évidence. En résolvant chaque jour le problème proposé par votre quotidien favori, vous ne ferez plus de la programmation sans le savoir.
Mais ce document ne cherche pas à présenter le Sudoku d’une manière exhaustive. D’autres éléments concernant ce jeu peuvent être trouvés dans l’article de Wikipédia.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Yan Georget