
Les calculateurs analogiques
Dans les années 1950 et 1960, bien avant les jeux vidéo et les effets spéciaux, bien avant le Web et Internet, et surtout bien avant la notion même d’ordinateur individuel, impensable à cette époque du fait du coût, de l’encombrement et de la délicatesse des machines, il existait déjà des ordinateurs — sous une autre appellation, certes. Mais il existait aussi un type de calculateur qu’aucun moins de quarante ans n’a probablement jamais manipulé, et peut-être même jamais vu : les calculateurs analogiques.
C’est ce que nous rappelle par exemple la consultation d’un livre de 1959 sur les « Machines à calculer électroniques » [1], dont plus du tiers est consacré à ces calculateurs. Comment ces étranges machines fonctionnent-elles ?
L’analogie entre systèmes physiques
Dans les classes scientifiques du lycée, les élèves abordent deux grands types de systèmes physiques dynamiques : les systèmes amortisseur – masse – ressort d’une part et les circuits électriques résistance – bobine – capacité (les fameux systèmes RLC) d’autre part. Dans les deux cas, des équations différentielles permettent de déterminer l’évolution des variables du système, à partir de leurs valeurs initiales.
Il apparaît rapidement qu’il existe des couples de systèmes, mécanique d’une part et électrique de l’autre, qui peuvent être modélisés par la même équation ou système d’équations différentielles : ces systèmes sont dits analogues. Cette analogie peut être mise à profit pour étudier la dynamique d’un système donné à l’aide d’un système plus aisément manipulable et qui lui soit analogue.
 |
 |
|
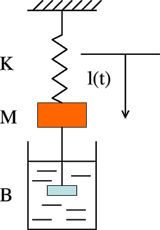
| Système mécanique oscillant amorti. L’équation différentielle modélisant ce système est M.l’’(t) + B.l’(t) + K.l(t) = 0 avec l(0) = l0, où l est la position du centre de gravité de la masse par rapport à une origine donnée. |
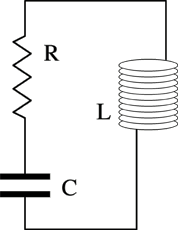
Système électrique oscillant amorti, dit RLC. Une équation différentielle modélisant ce système est RC.u’’(t) + LC.u’(t) + u(t) = 0 avec u(0) = u0, où u est la tension aux bornes du condensateur. |
Ces deux systèmes sont dits analogues, car modélisables par la même équation différentielle :
A.x’’(t) + B.x’(t) + C.x(t) = 0.
Ils possèdent les mêmes comportements : l’un peut servir à étudier l’autre.
Chacun des deux peut être utilisé pour étudier l’évolution de x dans le temps, c’est-à-dire résoudre, par simulation, l’équation différentielle.
Le circuit électrique est cependant beaucoup plus adapté, car les valeurs de R, L et C peuvent être très facilement modifiées.
Il est ainsi beaucoup plus facile, en général, de composer un circuit électrique « à façon » et d’en étudier expérimentalement la dynamique à travers des points de mesure bien choisis, que de tenter d’étudier directement la dynamique du système mécanique d’origine. Un des avantages du dispositif électrique est que les valeurs des tensions se mesurent aisément et avec une bonne précision. Elles peuvent de plus être affichées directement sur des dispositifs tels que des tables traçantes ou des oscilloscopes. Voilà donc le principe du calculateur analogique électronique : offrir une panoplie de composants et des facilités de connexion pour réaliser un circuit dont la dynamique mesurable sera, sinon identique, du moins similaire à celle du système étudié.
Du point de vue mathématique, le calculateur analogique permet de résoudre un ensemble d’équations différentielles, quelle que soit la nature du système dynamique réel que cet ensemble modélise. Or les équations différentielles sont omniprésentes en science. Que le système que l’on souhaite étudier soit mécanique, hydraulique, voire biologique ou économique, il peut être modélisé par un ensemble de telles équations. Si les composants du circuit sont convenablement agencés, alors les tensions mesurées à leurs bornes sont censées évoluer comme les variables du système : on dit que le circuit électrique simule le système. Cela explique certainement pourquoi autant d’efforts ont été développés pour mettre en œuvre de tels dispositifs de calcul, d’abord mécaniques, puis électriques et électroniques.
Un foisonnement de dispositifs
On peut caractériser le calcul analogique, plus largement encore, par la mise en œuvre d’un dispositif physique dont les mesures, à valeurs continues, de certaines propriétés fournissent la résolution d’une classe de problèmes.
À ce titre, la règle à calcul, unique dispositif portable et rapide de calcul des ingénieurs et des étudiants en science avant l’arrivée des calculatrices de poche au début des années 70, est bien un dispositif de calcul analogique, puisque le résultat d’une opération, telle qu’une multiplication, mais aussi l’extraction d’une racine carrée ou le calcul d’un cosinus, revient à une mesure de distance sur la règle.
La lecture du livre « Machines à calculer électroniques analogiques et arithmétiques » de 1959 fait découvrir de nombreux autres dispositifs de calcul analogique plus ou moins génériques, tels que les cuves rhéographiques, utilisées pour la résolution d’une certaine classe d’équations aux dérivées partielles, ou encore un analyseur harmonique qui, par l’emploi ingénieux de plusieurs sphères mobiles, permettait de calculer les coefficients de développement en série de Fourier d’une fonction y(t) donnée.
Ce foisonnement de dispositifs a progressivement décliné, conséquence d’abord de la mise en œuvre des machines analogiques électroniques, elles-mêmes supplantées dans les années 1970 par le calculateur arithmétique, que nous appelons maintenant « ordinateur », dispositif universel de calcul. Les équations différentielles et aux dérivées partielles y sont résolues grâce à des schémas de calcul itératifs appliqués à des équations adéquatement discrétisées.
L’analyseur différentiel
Parmi les nombreux dispositifs mécaniques de calcul analogique développés avant que les progrès de l’électronique ne permettent la réalisation des composants nécessaires, certains ont rencontré le succès. Ainsi, en 1931, Vannevar Bush, le même qui imagina un réseau de connaissances, Memex, dans lequel beaucoup voient une préfiguration du Web, terminait la réalisation de l’ « analyseur différentiel », dont le module de base était un intégrateur à disque.
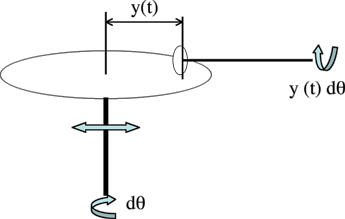
Principe de l’intégrateur à disque.
Le dispositif est constitué d’un disque horizontal, qui tourne à vitesse angulaire constante. La roulette qui s’appuie sur le disque est entraînée par son mouvement. La distance de son point d’appui avec le centre du disque, y, varie dans le temps, soit que l’axe vertical du disque se déplace (de droite à gauche sur la figure), soit que la position de la roulette soit modifiée. Quand le disque tourne d’un angle infinitésimal dθ, soit pendant un intervalle de temps βdτ, l’axe de la roulette tourne d’un angle α y(τ) dθ. Pendant un intervalle de temps [0, t], l’axe de la roulette tourne donc d’un angle α ∫ y(τ) β dτ. Un compteur de tours placé sur l’axe horizontal restitue donc la mesure de l’intégrale (de 0 à t) : ∫ y(τ) dτ, à un facteur de proportionnalité près. Il suffit, par exemple, de faire commander le déplacement d’un stylet par une vis sans fin placée sur cet axe pour tracer la courbe intégrale.
Ce type de calculateur fut utilisé pour la résolution de nombreux problèmes complexes, en particulier dans le domaine militaire. Les connexions entre les intégrateurs étaient initialement purement mécaniques. Aussi l’analyseur différentiel disposait-il d’amplificateurs de couples, reposant sur un principe similaire à celui du cabestan, où des cordages enroulés sur un tambour permettent de décupler les forces. La résolution d’un système différentiel relevait du jeu de Meccano : il s’agissait d’assembler moteur, engrenages, vis sans fin, et intégrateurs à façon.
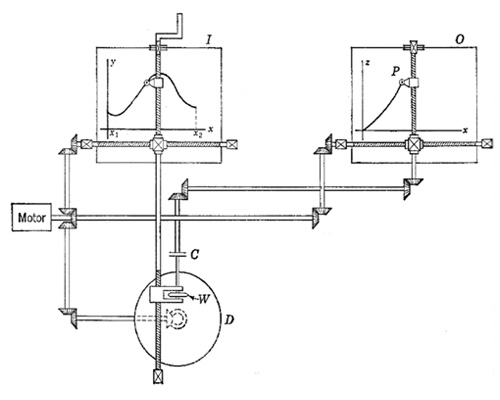
Intégration d’une fonction à l’aide d’un intégrateur différentiel.
L’entrée du dispositif est constituée de la manivelle qui permet à l’opérateur de suivre la courbe au fur et à mesure que la variable indépendante croit. Cette variable est spécifiée par la rotation, à vitesse constante, du moteur. Ici, c’est la position de la roulette W sur le disque qui varie. La sortie de l’intégrateur commande le mouvement en ordonnée du stylet d’une table traçante ; le mouvement en abscisse est commandé par le moteur, dont la rotation spécifie, là aussi, la variable indépendante. Source : An Introduction to Analog and Hybrid Computing, Bernd Ulmann, téléchargeable en PDF (2,9 Mo).
À ce propos, un calculateur comportant plusieurs intégrateurs mécaniques à disque a été réalisé en Meccano : voir Tim Robinson’s Differential Analyzer, notamment cette vidéo tout à fait étonnante, malgré la mauvaise qualité du son, qui le montre en fonctionnement (vidéo Windows Media, 5 min environ).
Le calculateur analogique à opérateurs électroniques
Le développement des calculateurs analogiques électroniques a indéniablement constitué un progrès important, en termes de fiabilité, de précision, d’encombrement et de facilité de mise en œuvre et d’utilisation.

L’ACONIT (association pour un conservatoire de l’informatique et de la télématique) conserve à Grenoble un exemplaire du calculateur analogique à lampes SEA OME P2. Source : ACONIT.
Bien entendu, les calculateurs analogiques ont bénéficié de la technologie des transistors. L’Alpam est ainsi une petite machine utilisée en particulier pour l’enseignement.

Calculateur analogique Alpam conservé par l’ACONIT à Grenoble. On distingue à droite le panneau de connexion des opérateurs et à gauche en bas les potentiomètres. Source : ACONIT.
Un calculateur analogique électronique constitue un outil générique de résolution d’équations différentielles. Son principe consiste à représenter les variables de ces équations par des tensions électriques et les opérateurs mathématiques par des opérateurs électroniques connectés conformément aux équations du système différentiel.
© ACONIT
Il est important de souligner que la résolution sur un tel calculateur d’un système d’équations différentielles ne produit pas l’expression mathématique des fonctions solutions ; seules les trajectoires des variables d’état, pour un jeu donné de valeurs des paramètres et des conditions initiales, sont produites.
Les opérateurs analogiques
Les opérations principalement concernées sont l’addition (ou la soustraction), l’intégration par rapport à une variable indépendante (souvent le temps), la multiplication par des constantes et la multiplication de variables, ou encore la génération de fonctions. L’électronique des amplificateurs opérationnels permet de réaliser les opérateurs correspondants.
Ces opérateurs principaux sont décrits ci-dessous par leur fonction et le symbole utilisé dans le dessin d’un schéma fonctionnel. Les ei désignent les variables d’entrée, s est la variable de sortie.
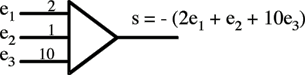
Sommateur (ou additionneur).
Changeur de signe (ou inverseur analogique).
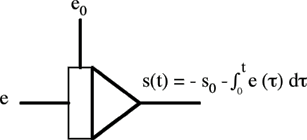
Intégrateur.
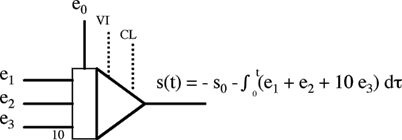
Intégrateur sommateur. Les informations VI et CL sont des commandes logiques donnant l’ordre d’intégrer ou non.
Multiplication par une constante (potentiomètre). La valeur de α est comprise entre 0 et 1. Pour multiplier par des valeurs supérieures, il faut jouer avec les facteurs d’amplification en entrée des opérateurs suivants.
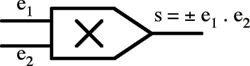
Multiplication de variables. Le signe + ou – est choisi par l’utilisateur.

Génération de fonction.
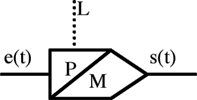
Mémorisation temporaire (ou poursuite-mémoire, PM). L est une commande logique. Si L = 0, s(t) = e(t) ; si L = 1, s(t) conserve la valeur de e(t) au moment du passage de L de 0 à 1 ; cette valeur est perdue quand L repasse de 1 à 0.
Les machines de forte puissance disposaient de 300 à 400 intégrateurs, fonctionnant sous une tension électrique de ± 100 volts, pour espérer une précision de l’ordre de 10-4 à 5.10-5. Les machines moins puissantes proposaient de 200 à 250 intégrateurs, sous une tension électrique de ± 10 volts pour une précision de 10-3 à 10-4.
Le schéma fonctionnel
Pour résoudre un système différentiel sur un calculateur analogique, il faut établir le schéma fonctionnel correspondant, c’est-à-dire la connexion des opérateurs analogiques qui réalise la ou les équations. Raymond Bouttaz explique dans la vidéo suivante comment établir le schéma fonctionnel associé à l’équation différentielle y’’ + a.y = 0.
© ACONIT
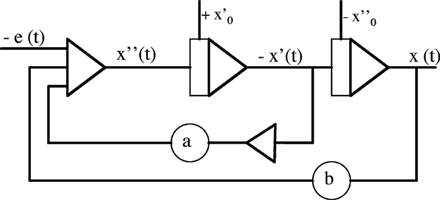
Pour un exemple un peu plus complexe, soit l’équation différentielle x’’(t) + a.x’(t) + b.x(t) = e(t), avec x(0) = x0 x’(0) = x’0. x(t) est la variable du phénomène étudié, x’(t) et x’’(t) sont les dérivées première et seconde de x(t), e(t) est une variable d’excitation connue. La solution de cette équation est une fonction x(t) qui satisfait l’équation et les conditions initiales.
L’équation peut se réécrire sous la forme –x’’(t) = – e(t) + a.x’(t) + b.x(t), qui conduit très naturellement au schéma fonctionnel suivant :
Voici un troisième exemple, en biologie, plus précisément en dynamique des populations. Il s’agit d’étudier les variations d’effectifs de deux populations, de prédateurs et de proies, en interaction. Un tel système fut formalisé au milieu des années 1920, indépendamment par Alfred Lotka et Vito Volterra, qui ont donné leur nom au système différentiel résultant.
L’effectif de la population de proies (des lapins, par exemple) est noté x ; celui des prédateurs (des renards par exemple) est noté y. On fait l’hypothèse que les prédateurs se nourrissent exclusivement des proies, si bien que, en leur absence, leur effectif ne pourrait que décroître par suite de la mortalité à un taux c. À l’inverse, en l’absence de prédateurs, la population des proies s’accroîtrait sans limite, à un taux a. Sans interaction, la dynamique de ce système de deux populations s’écrirait :
x’(t) = a . x(t) et x(0) = x0
y’(t) = – c . y(t) et y(0) = y0
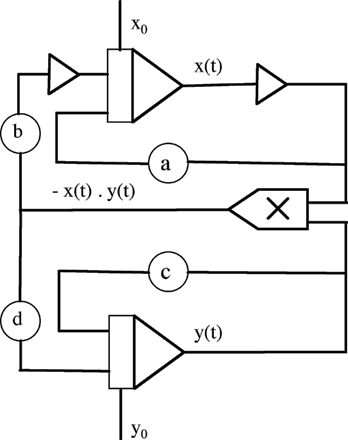
Mais les proies et les prédateurs se rencontrent… Si le nombre potentiel de rencontres à tout instant t est le produit x(t) . y(t), seule une très faible proportion donne lieu à prédation. La capture de proies réduit bien entendu la population des proies, mais, par l’apport de nourriture, contribue à faire croître celle des prédateurs. Le système différentiel suivant, non linéaire, rend compte de cette dynamique d’interaction :
x’(t) = a . x(t) – b . x(t) . y(t) ; x(0) = x0
y’(t) = – c . y(t) + d . x(t) . y(t) ; y(0) =y0
La résolution sur un calculateur analogique met en œuvre le schéma fonctionnel suivant (ne pas oublier que les intégrateurs inversent le signe de leurs entrées) :
Mise en œuvre du schéma fonctionnel
Une fois le schéma fonctionnel obtenu, il est nécessaire de normaliser les variables du système différentiel de façon à ce qu’elles varient dans les plages de fonctionnement admissibles du calculateur. En effet, x peut être connue pour varier dans l’intervalle [xmin, xmax], mais les tensions mesurées sur le calculateur ne peuvent varier, par exemple, que dans l’intervalle [- 10 volts, + 10 volts].
Il s’agit ensuite de connecter les différents opérateurs en suivant le schéma fonctionnel, de fixer les facteurs d’amplification des entrées de ces opérateurs, les conditions initiales sur les intégrateurs et de positionner correctement les potentiomètres de multiplication par une constante. Ce travail de câblage s’effectue, à la main, dans le mode VI (valeur initiale) du calculateur.
Il est ensuite possible de passer dans le mode CL (calcul). Dans ce mode, les opérateurs fonctionnent, les intégrateurs intègrent les valeurs proposées sur leurs entrées en fonction du temps. Les tensions associées aux variables d’état (ici x’’(t), x’(t), x(t)) évoluent dans le temps comme le stipule le système différentiel : les phénomènes modélisés par les équations sont simulés.
Un troisième mode, Me (mémoire), permet de figer temporairement le calcul.
Résultats
Le calcul analogique ne permet pas l’obtention de l’expression analytique de la fonction solution du système différentiel, mais elle permet d’étudier l’évolution dans le temps de ses variables. À chaque simulation, les valeurs des paramètres et des conditions initiales peuvent être modifiées et l’impact sur l’évolution des variables étudiées.
© ACONIT
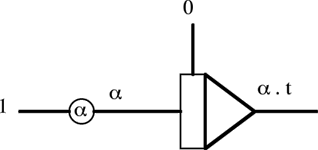
L’évolution des variables est tracées sur papier millimétré à l’aide d’une table traçante, ou visualisées sur un oscilloscope. En ordonnée figure la tension correspondant à la variable d’intérêt, en abscisse la variable indépendante, généralement le temps, dont la valeur est très facilement générée par le circuit suivant :
D’autres méthodes plus évoluées (pour l’époque), telle que l’enregistrement sur magnétophone, permettaient de stocker les résultats.
Et notre système d’équations proies-prédateurs, que donne-t-il ? Son comportement est périodique ; les effectifs des populations oscillent en décalage de phase : lorsque la population des prédateurs est maximale, le taux de prédation l’est aussi. Il est assez facile de comprendre qualitativement ce comportement oscillatoire.
Pour visualiser l’évolution des populations selon la valeur des paramètres, nous vous proposons une applet du site CultureMATH. Les équations y sont résolues non par une méthode analogique, mais à l’aide d’une méthode numérique qui s’exécute sur votre calculateur arithmétique.
Les opérateurs « mixtes »
Le développement des circuits logiques a rapidement bénéficié aux calculateurs analogiques à travers l’introduction d’opérateurs mixtes, mêlant valeurs continues et valeurs booléennes.

Comparateur. e1 et e2 sont des variables continues, L est une variable booléenne.
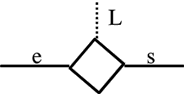
Porte analogique (l’équivalent d’un interrupteur). e est une entrée analogique, s la sortie analogique ; L est une variable booléenne : s = si L alors e sinon 0.
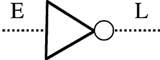
Inverseur logique. E et L sont des variables booléennes : L = ¬ E (non E). À ne pas confondre avec le changeur de signe analogique.
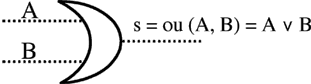 |
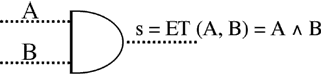 |
| Opérateurs booléens traditionnels OU et ET. | |
Le montage suivant est un exemple d’utilisation des opérateurs mixtes. Il permet de faire un choix entre e1 et e2 en fonction de a et b. Il correspond à une instruction bien connue dans les langages de programmation, l’expression if…then…else : s = if a > b then -e1 else -e2.
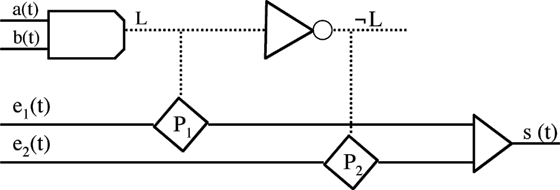
Montage utilisant les opérateurs mixtes.
Si a(t) > b(t), alors L est vrai, et l’interrupteur P1 est fermé et P2 est ouvert : s(t) = – e1(t). Sinon, L est faux, l’interrupteur P1 est ouvert, P2 fermé et s(t) = – e2(t).
Analogique versus numérique
Dans les années 1960, les calculateurs analogiques et numériques possèdent chacun des avantages et des inconvénients propres, qui conditionnent leur utilisation. Voici un exemple de projet pour lequel le calcul analogique a été jugé plus performant.
© ACONIT
Un calculateur analogique fonctionne en temps réel, voire beaucoup plus vite, d’un facteur 10 à 100 suivant la qualité de ses opérateurs. Tous ces opérateurs travaillent simultanément, en parallèle. Par contre, la précision des résultats est moyenne, dépendante de cette même qualité des opérateurs, et sa capacité de calcul est directement liée au nombre d’opérateurs disponibles. Il requiert de plus une étape de câblage manuel fastidieuse et sujette à erreurs. Enfin, il est spécialisé, dédié à la résolution de systèmes différentiels.
À l’inverse, le calculateur numérique est un outil de calcul universel, doté d’une grande capacité de mémoire. Mais à l’époque, ces calculateurs étaient beaucoup plus lents que maintenant. Leur programmation, pour être efficace, demandait à être faite dans des langages de bas niveau, typiquement en assembleur, car les compilateurs de l’époque ne produisaient pas de code exécutable aussi efficace.
Les calculateurs hybrides
Il était donc assez naturel d’associer ces deux types de calculateurs. Ainsi apparurent au début des années 1960 les calculateurs hybrides. Les deux machines fonctionnant avec des signaux électriques différents (continus pour l’analogique et successions binaires pour le numérique), le couplage nécessitait une liaison à travers des interfaces analogique/digital et digital/analogique. Les tâches étaient réparties en fonction de leur nature : pour l’analogique, la résolution de systèmes différentiels ; pour le numérique, les opérations algébriques et logiques complexes. Les utilisateurs se devaient de bien connaître le fonctionnement de l’ensemble pour se livrer à une analyse approfondie du problème à traiter et répartir habilement les tâches.
Les capacités du calculateur arithmétique pouvaient également être employées à réaliser le câblage du calculateur analogique qui lui était couplé, en fonction d’un schéma fonctionnel correctement codé : le calculateur analogique devenait programmable.
L’enseignement du calcul analogique
Jusque dans les années 1970, le calcul analogique a fait partie des enseignements de nombreuses filières scientifiques et techniques. Ainsi à Grenoble, il était enseigné en maîtrise d’informatique et dans les écoles d’ingénieurs ENSERG et ENSIMAG. En filière informatique, les cours étaient donnés par le Professeur Raymond Bouttaz, que l’on a vu plus haut expliquer les principes du calcul analogique. Les travaux pratiques s’effectuaient sur des machines Alpam à transistors, mais à chaque séance, un binôme était affecté à une machine de la génération précédente à lampes, plus capricieuse, qui sanctionnait parfois, par une décharge électrique fort désagréable, les manipulations hasardeuses… Ces TP, assurés par l’un des auteurs de cet article (Alain Brochier), ont été suivis par l’autre (François Rechenmann).
Ces cours et travaux pratiques se justifiaient à l’époque par l’actualité de ces techniques de calcul analogique. Mais ils apportaient également, à travers l’expérimentation directe et manuelle, une compréhension profonde des équations différentielles et des systèmes dynamiques. L’emploi désormais généralisé des ordinateurs pour la résolution numérique de ces équations implique une distance plus importante qui interdit peut-être une compréhension aussi intuitive des systèmes dynamiques.
Quel avenir pour les technologies analogiques ?
L’analogique a encore longtemps survécu en informatique, au niveau des capteurs de données. Jusqu’à peu, les images vidéo, par exemple, devaient faire l’objet d’un transfert analogique-digital. L’avènement des caméras numériques a fait disparaître ces interfaces. Alors, le calcul analogique est-il définitivement voué à l’oubli ?
Peut-être pas, si l’on en croit l’annonce en 2005 [2] de la réalisation d’une puce de calcul analogique (citée dans [3]). Rassemblant plus de 400 composants interconnectables à la demande, ce circuit VLSI peut être utilisé en tant que co-processeur d’un ordinateur pour résoudre des systèmes différentiels jusqu’à l’ordre 80. Présentée comme étant 400 fois plus rapide qu’une station de travail dotée de procédures d’intégration numérique, cette « puce » consomme moins de 2 % de l’énergie consommée par un processeur classique pour résoudre le même problème. À suivre…
Références bibliographiques :
[1] M. Pélegrin, Machines à calculer électroniques analogiques et arithmétiques, Dunod, 1959
[2] G.E.R. Cowan, R.C. Melville, and Y.P. Tsividis, « A VLSI analog computer/math co-processor for a digital computer » in Proc. 2005 IEEE Solid-State Circuits Conf., San Francisco, CA, pp. 82-83, Feb. 2005
[3] Kent H. Lundberg, « History of Analog Computing », IEEE Control Systems Magazine, vol. 25, no. 3, pp. 22-28, June 2005
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

