L’épreuve Million ou les tourments d’un mathématicien amoureux
Chapitre 1

Dessin : © Paul Gendrot
Valérie était en larmes. D’un geste lent mais définitif, elle repoussa son assiette de quelques centimètres. Relevant ensuite la tête en tremblant légèrement, elle tamponna ses yeux avec sa serviette et, après une vague hésitation, se leva en hoquetant.
— Ma chérie…
France Million, la cinquantaine blond cuivré qu’elle aurait voulu vénitien, était restée une femme simple en dépit de l’éclatante réussite professionnelle de son mari. Simple, et maigre. Alors que la plupart de ses amies avaient pris leur lot de kilos superflus au fil des années, elle s’amusait encore, certains dimanches, à enfiler sa robe de mariée et à esquisser des pas de valse devant le grand miroir en pied du grenier. Maigre, et simple.
Mais, à cette heure, elle avait d’autres chats à fouetter, si tant est qu’elle fût femme à fouetter qui que ce soit. Elle détestait ces prises de bec entre sa fille Valérie, dont elle était si fière, et son mari Stanislas, objet de toutes ses attentions, dont elle redoutait en permanence les sautes d’humeur dévastatrices.
— Ma chérie… Ton père pense d’abord à ton bien…
Stan paraissait plus grand assis que debout. À cause, probablement, de ses membres trop courts, soi-disant qu’il aurait « fait un peu de rachitisme » dans les années de l’immédiat après-guerre, avant le lait Mendès France. Il fulminait, mais conservait au coin des lèvres une sorte de mauvais sourire dominateur. Sa calvitie en couronne faisait apparaître un étonnant contraste entre le rose des joues et les reflets opalescents du cuir chevelu.
— Un mariage, après tout, c’est pour toute la vie… Enfin, au moins pour longtemps…
Mais Valérie, mâchoires serrées, descendait déjà les marches du perron. C’est précisément cet instant que Stan choisit pour passer à l’action. Avec une fulgurance dont plus personne ne le croyait encore capable, et certainement pas sa femme, il bondit de sa chaise, traversa la salle à manger, le living, et, avant qu’elle n’ait pu y pénétrer, se retrouva devant la Clio de sa fille (celle-là même qu’il lui avait offerte pour son CAPES d’histoire), lui bloquant résolument le passage.
— Tu as vingt-cinq ans…
Il n’avait vraiment pas l’air d’humeur à négocier. Un peu comme le jour où M. Villeret, sous prétexte qu’il est pharmacien, avait voulu lui faire refaire tout le circuit d’arrivée d’eau de sa maison de campagne, arguant que les canalisations n’étaient pas aux normes et que le défaut de pente engendrerait des « foyers septiques ». Sceptique, Stan l’était resté jusqu’au bout, aussi ému du risque de nids à microbes que de son premier raccord en pvc. Il y avait eu une scène mémorable sur le carrefour, juste devant la pharmacie. L’affaire s’était évidemment terminée devant le tribunal de commerce, mais Stan s’était défendu mordicus et, après plusieurs années, il avait eu gain de cause.
— Tu as vingt-cinq ans, ma fille…
— Je sais bien, papa !
— … et il est hors de question que tu épouses un garçon qui n’a pas de métier !
— Mais, papa, il est chercheur, mathématicien, c’est un scientifique ! C’est un métier, ça ! D’ailleurs il cotise à la sécu…
— Ça ne veut rien dire. Mathématicien, ce n’est pas un métier, pas un vrai…
Arc-bouté, enraciné dans ses certitudes, Stanislas Million aurait pu repousser les assauts de tous les rhéteurs des mondes antique et moderne réunis. La colère sourdait des prunelles amandines de Valérie.
— C’est quoi alors, M. Je-sais-tout ?
— C’est… c’est… un adjectif, voilà !
Voir traiter son Lucien d’adjectif, c’était plus que la jeune fille ne pouvait supporter. Et dire qu’il avait brillamment soutenu sa thèse de théorie des nombres quelques mois auparavant… Il fallait frapper vite et fort, étourdir l’adversaire avant de porter l’estocade. Tant pis pour les âmes sensibles.
— Papa, j’attends un enfant.
Elle vit immédiatement qu’elle avait pris l’avantage : tel un taureau estourbi par le picador, il fit deux pas de côté, lui laissant enfin la possibilité de s’asseoir au volant.
— Hein ? Un enfant ? Mais, tu n’es…
Stan était blême. Les joues, roses quelques instants auparavant, avaient viré au nacré façon saturnisme chronique. Quelques gouttes de sueur glacée perlaient sur le front et la moustache.
— Papa, tu l’as dit toi-même, j’ai vingt-cinq ans…
— Mais… mais… il n’a pas de métier… Ça ne sert à rien, les mathématiques… Si encore il était prof, comme toi, mais chercheur, chercheur en maths, ça n’a aucun sens… Et puis, d’ailleurs, il cherche quoi ? Qu’y a-t-il donc encore à chercher ?
— Bien sûr qu’il y a matière à chercher ! C’est… très important même.
Devinant un sourire incrédule, entre mépris et défi, sur les lèvres paternelles, la jeune femme ajouta :
— Il y a des masses de conjectures, sur lesquelles ils travaillent tous…
— Les conjonctures, on nous dit tous les jours qu’elles vont mal, qu’elles sont mauvaises, que c’est la crise…
— Con-jec-ture, papa, pas con-jonc-ture. C’est différent. Les conjectures, ce sont des idées de théorèmes, enfin de ceux qui ne sont pas encore de vrais théorèmes, ceux qu’on attend sans savoir…
— Si c’est une fille ou garçon ?
Elle sourit. Au moins, il n’avait pas perdu son sens de l’humour. Et le gros de la tempête était visiblement passé.
— Si tu veux, sauf que, dans ce cas-là, il y a beaucoup plus que deux possibilités. Des milliards…
— Un petit Million, ça me suffira. C’est pour quand ?
— Septembre. On aura le temps de tout préparer. D’ailleurs, maman est au courant…
— Pas si vite, fillette, je n’ai pas dit mon dernier mot !
Pas à dire, il encaissait bien et il récupérait vite. Il avait à présent les yeux brillants et ses joues avaient presque retrouvé un semblant de couleur. Valérie sortit de la voiture. S’il fallait négocier, autant le faire dans un endroit confortable.
— Viens, on rentre à la maison.
En les apercevant s’asseoir calmement au salon, France les gratifia de regards reconnaissants.
— Ma chérie, tu veux ton dessert ?
— Non merci. Papa a une proposition à me faire.
Stan attrapa le gros cendrier en verre fumé et se mit à jouer avec l’éteignoir en forme de gourdin préhistorique. Un cadeau de mariage. Il semblait chercher à rassembler des souvenirs.
— Quand j’ai demandé la main de ta mère, j’avais juste un CAP. Je suis venu un dimanche. Il pleuvait. J’avais des fleurs, mais le bouquet était trempé. Beau-papa m’a fait entrer dans la pièce rouge, celle des réunions de famille, qu’il n’ouvrait que pour les grandes occasions…
Il jeta un rapide regard circulaire autour de lui, comme pour se rassurer de tout ce qui lui appartenait, tout ce qu’il avait gagné. Il avala sa salive, se passa brièvement la langue sur les lèvres, et reprit :
— Il m’a dit : « Vous avez votre CAP, bien, mais qu’est-ce que vous savez faire ? » Alors j’ai expliqué mes projets, d’où je venais et où je voulais aller, et nous nous sommes compris, nous avons parlé le même langage, concret, solide, réaliste…
— Papa, aujourd’hui, les choses ont changé.
— Peut-être, mais j’aimerais bien que ton Lucien-chercheur vienne me raconter à moi aussi comment il voit les choses, ce qu’il sait faire et ce qu’il cherche dans cette voie qu’il a choisie…
— Impossible ! C’est beaucoup trop compliqué, tu n’y comprendras jamais rien !
— Justement, Valou, j’ai juste mon certif, je n’y comprendrai certainement rien, mais je suis ton père. Alors, il faudra qu’il essaie.
Fût-ce à cause du « Valou », le premier depuis si longtemps, la jeune fille répondit doucement :
— Bon, d’acc, ’pa, il viendra, une fois, deux fois, peut-être trois fois, et il t’expliquera…
M. Million se renversa lentement sur son fauteuil. Il y avait si longtemps qu’il n’était pas retourné à l’école… Il allait laisser sa chance au blanc-bec…
Là-dessus, il s’endormit.
Il faut dire que, depuis quelques années, il faisait systématiquement une petite sieste après le repas.
Chapitre 2

Dessin : © Paul Gendrot
La première rencontre était prévue pour lundi à 19 heures. Lucien, qui avait contracté très jeune l’habitude d’arriver systématiquement en retard de quelques minutes à ses rendez-vous, fut ce jour-là scrupuleusement ponctuel. France lui ouvrit la porte. Elle avait prévu de rester très neutre, mais le jeune homme avait un bon sourire qu’elle ne put s’empêcher de rendre.
— Bienvenue, M. Faus, mon mari vous attend.
— Bonjour. Merci, Madame Million. Est-ce que Val est là aussi ?
Il savait très bien que la réponse serait négative. Les tourtereaux avaient considéré qu’il serait préférable que Lucien affrontât seul ses futurs beaux-parents et Valérie s’était éclipsée en fin d’après-midi, prétextant une réunion pédagogique en marge de son stage en classe de seconde.
Lucien était plutôt grand, mince, avec un regard noir rehaussé de sourcils bien dessinés. Il y avait quelque chose de naïf dans le haut de son visage, qui contrastait avec une sorte de détermination de la bouche et de la mâchoire. France l’introduisit au petit salon-bibliothèque, où attendait son mari, calé derrière le bureau qu’il n’utilisait plus depuis des années. C’était assis à cette table qu’il avait, au début, établi les devis et les factures. Mais dès que l’entreprise avait pris de l’envergure, il avait embauché une aide-comptable pour le décharger de ces tâches pour le moins fastidieuses.
— Asseyez-vous, jeune homme !
— Merci, Monsieur.
Au moins, il était poli. Avec sa raie sur le côté, son pull marine en V et sa serviette en cuir, il faisait plutôt bon genre, quoique un peu intemporel. Cela dit, il aurait tout de même pu mettre une cravate.
— Alors, comme ça, vous faites des mathématiques ?
— Oui, enfin de la théorie des nombres…
— Et vous voulez épouser ma fille ?
Stan était assez content de cette brutale entrée en matière. Il était très curieux de voir comment le cadet s’en sortirait. À en juger par la goutte de sueur qui avait perlé sur son front, il avait au minimum suscité une certaine émotion.
— Nous le voulons tous les deux… Et…
— Et ?
— Nous aimerions beaucoup avoir votre accord, à Mme Million et à vous.
— …
Au dernier moment, Stan réfréna le « Et sinon ? » qu’il avait au bout des lèvres. Quelque chose lui disait que ce garçon était du genre à relever les défis et à accepter le combat frontal. Il décida donc d’entrer sans plus attendre dans le vif du sujet.
— On verra ça… Vous êtes donc dans les chiffres ?
— Oui, enfin, plutôt dans les nombres.
— C’est pareil, non ?
— Disons que les chiffres servent à écrire les nombres. Par exemple, 3 est un chiffre, qui est aussi un nombre, et 32 est un nombre qui s’écrit avec deux chiffres. Les chiffres arabes, de 0 à 9, sont les plus utilisés, mais il y a aussi les chiffres romains…
— Sans compter le chiffre d’affaires !
C’était parti un peu vite, il fallait bien détendre l’atmosphère.
— Si vous voulez…
— Et alors, aligner des chiffres, ou même des nombres, ça vous donne quoi dans la vie ?
— Je ne les aligne pas, j’y pense, je réfléchis sur leur nature, leur structure.
Stanislas Million, plombier, écarquilla les yeux, se frotta les paupières, ouvrit la bouche, la referma, s’éclaircit la voix, et se lança finalement.
— Mais, voyons, tous le monde sait ce que c’est qu’un nombre ! On commence par un, et puis on ajoute un, ça fait deux… Vous n’allez pas me faire croire qu’on vous paie, même pas cher, pour réfléchir sur des idées qu’on utilise depuis que le monde est monde ?
C’était au tour de Lucien d’être mal à l’aise. Il n’allait pas s’en sortir comme ça, il lui fallait une comparaison. Il choisit la première qui lui vint à l’esprit.
— Quand vous allumez la lumière, vous vous servez de l’électricité, n’est-ce pas ?
— Certes…
— Mais vous n’avez pas besoin pour cela de connaître la nature des électrons et la structure fine de la matière ?
— Au fait, jeune homme…
— Eh bien, c’est la même chose pour les nombres : tout le monde s’en sert, les mathématiciens y réfléchissent.
M. Million se pencha en avant, le regard acéré et les lèvres humides.
— Sauf qu’il a bien fallu comprendre les électrons pour domestiquer l’électricité… Alors que, compter, ma foi…
Lucien croisa les jambes. Ce fut précisément le moment que Mme Million choisit pour entrer :
— Voulez-vous quelque chose à boire ? Alcoolisme, ou boissons fraîches ?
— Un petit whisky avec des olives, répondit Stan sans lever les yeux.
— Juste de l’eau minérale, dit Lucien, si vous avez, merci.
Il attrapa son siège des deux mains, et dit doucement :
— Mais, vous, M. Million, entre les vases communicants, les siphons, les joints, les soudures qui tiennent et celles qui ne tiennent pas, il y a bien des jours où vous avez envie de savoir comment ça marche, non ? Des jours où vous êtes un peu plus curieux que d’autres ?
Il avait, à cet instant, l’air d’un vrai gosse en train de démonter le poste de radio de son grand-père. Stan repensa à ses Dinky Toys et lui accorda, sinon le quitus, du moins le bénéfice du doute.
— Bon. Admettons que vous soyez curieux et que, moi, je veuille bien payer des impôts pour vous calmer…
— D’autant, qu’évidemment, les nombres, ça peut servir aussi, vraiment…
— À quoi, par exemple ?
— À garder le code secret de votre carte bleue.
— Et comment ça ?
— C’est un peu compliqué, mais, disons qu’on utilise les nombres premiers.
— Les nombres entiers, vous voulez dire…
— Non, les nombres premiers, ceux qu’on ne peut pas retrouver comme produit de deux nombres plus petits.
— Là, je ne vous suis plus.
— Prenez 12 : c’est 4 fois 3, il n’est pas premier. Mais 11, on ne peut pas le retrouver de cette manière, il est premier.
— OK. Et qu’est-ce que ça a à voir avec ma carte bleue ?
— On veut garder votre numéro secret : ça revient à fabriquer une serrure facile à fermer et très difficile, sinon impossible à ouvrir.
— Si vous voulez.
— Lorsque vous multipliez 11 par 13, vous trouvez 143, c’est facile.
— Oui, bien sûr.
— Mais si vous deviez retrouver 11 et 13 à partir de 143, ce serait beaucoup plus délicat, non ?
— Je ne sais pas, je n’y ai jamais réfléchi…
— Vous admettez donc que cela nécessiterait une réflexion !
— Vous marquez un point, jeune homme.
— C’est le principe de la serrure : on choisit de très grands nombres premiers, disons des nombres de cent ou cent cinquante chiffres…
— Hou la la !
— … on fait leur produit, c’est facile, on obtient un nombre de trois cents chiffres, et là, il est presque impossible de revenir en arrière…
— De retrouver les deux nombres de départ ?
— Exactement ! C’est comme ça qu’on protège votre argent !
— Pas mal…
Stan contempla un instant son whisky, attrapa une olive avec trois doigts de sa main droite, la croqua et but une gorgée qu’il sirota en jouant avec le noyau. Il regardait son interlocuteur avec la mine d’un badaud qui s’est fait bluffer par un bateleur de foire et cherche le truc tout en pressentant qu’il ne le trouvera pas.
Tout à coup, son visage se tendit :
— C’est pas mal, votre histoire, mais quand les ordinateurs auront trouvé tous les nombres premiers et fait tous les produits, vous serez gros Jean comme devant ?
— Les ordinateurs ne trouveront jamais tous les nombres premiers…
— Ha, ha ! Il paraît qu’il ne faut jamais dire jamais !
— Sauf si on peut le prouver. Et en mathématiques, il arrive que l’on puisse… Dans le cas qui nous occupe, c’est facile : il y a une infinité de nombres premiers !
— Que voulez-vous dire par là ?
— Si l’on rangeait tous les nombres entiers sur les barreaux d’une échelle et que l’on peignait en rouge les barreaux correspondant aux nombres premiers, on pourrait monter jusqu’au ciel en n’utilisant que les barreaux rouges.
— Comment pouvez-vous en être si sûr ? Les arbres ne montent pas au ciel, les échelles non plus…
— Supposons que je multiplie entre eux tous les nombres entiers depuis 2 jusqu’à 101.
— Faites, je vous en prie.
Une certaine complicité transpirait dans cette invite.
— J’obtiendrais alors un grand nombre, en fait de l’ordre d’un milliard.
— Soit.
— Ce nombre est évidemment un multiple de 2, 3, 4, etc., jusqu’à 101. Vous êtes d’accord ?
— Oui, oui…
— Ajoutons alors 1 : nous obtenons un nombre impair, puisque le nombre de départ est multiple de deux. Mais ce nouveau nombre laisse aussi un reste de 1 lorsqu’on le divise par 3.
— Forcément : il est le suivant d’un multiple de 3. Stanislas semblait à présent assez excité.
— De même, reprit Lucien, son reste dans la division par 4, 5, ou 101 est égal à 1.
— Oui, je vois cela, dit Stan dans un soupir.
— Donc ce nombre ne peut être divisé que par des facteurs plus grands que 101 : ainsi, il existe des nombres premiers dépassant 101…
— Pourquoi des nombres premiers ?
— Parce que : ou bien notre nouveau nombre est premier, ou bien il est produit de facteurs premiers plus petits, mais qui tous dépasseront 101.
— Je ne suis plus très sûr de comprendre, dit Stan, visiblement un peu déçu, mais où vouliez-vous en venir ?
— À ceci : ce que nous avons fait avec 101, nous pouvons le refaire avec n’importe quel nombre… Il y a donc toujours un barreau rouge au-delà d’un barreau rouge !
— Ha ! Alors je peux dormir tranquille, mon argent est bien protégé !
— Sauf si un mathématicien invente un moyen de trouver facilement les facteurs d’un très grand nombre…
— Je vois… ce serait une raison de couper les crédits de la recherche plutôt que le contraire, non ?
M. Million semblait satisfait de son humour. Lucien ne répondit pas et avala d’un trait son verre d’eau en le regardant fixement.
Après quelques échanges polis sur des renseignements d’état civil et d’adresse, on convint d’un nouveau rendez-vous pour le lundi suivant. À l’évidence aucun des deux protagonistes n’était totalement parvenu à ses fins : Lucien sentait confusément qu’il n’avait pas convaincu Stanislas de son utilité sociale et ce dernier ne se résolvait pas vraiment à considérer ce gamin jongleur de nombres, aussi habile fût-il, comme un possible père pour ses petits-enfants.
Chapitre 3

Dessin : © Paul Gendrot
Le premier contact s’étant, somme toute, plutôt bien passé, ces dames furent invitées à la seconde rencontre. Il faisait beau. Mme Million en avait profité pour dresser la table dans le patio. Lorsque Lucien y pénétra, il aperçut Stanislas en grande conversation avec sa fille, apparemment à propos de la voiture de France, qu’il fallait remplacer : le premier voulait la revendre et la seconde la « récupérer ». Val avait relevé ses cheveux en un savant chignon à la grecque, juste assez décoiffé pour troubler la concentration du chercheur. Avec ses fines lunettes de métal aux reflets mauves et violets, elle était vraiment irrésistible.
Ce fut Stan qui tira le premier.
— J’ai parlé de votre histoire de nombres premiers avec un client avocat. Il m’a dit que le plus grand nombre premier avait été trouvé par ordinateur aux USA. Tenez, je l’ai noté.
Il tendit à Lucien un bon de commande de son entreprise, au dos duquel il avait inscrit au feutre noir
P = 26972593 – 1.
— Merci, je n’avais pas noté la valeur exacte, dit Lucien, mais ce n’est pas le plus grand nombre premier, c’est juste le plus grand nombre premier connu.
— Comment savoir s’il y en a d’autres, puisqu’ils sont inconnus ? demanda Valérie.
— Eh bien, comme je l’ai expliqué à ton père lundi dernier…
— … Les cartes bleues avalent des nombres premiers et elles ne risquent pas de mourir de faim ! interrompit Stan.
— Effectivement, on peut le dire comme ça… savoir qu’il existe autant de nombres premiers qu’on veut, une infinité, est une chose ; savoir reconnaître, décider si un nombre qu’on a écrit, avec tous ses chiffres, est premier, c’est une tout autre affaire.
— On fait des produits à partir de 2, on obtient un très grand nombre, puis on ajoute 1, et hop ! il y a un nouveau nombre premier, ajouta Stan, tout fier de lui.
— Oui, mais, malheureusement, cela ne permet pas de l’écrire, précisa Lucien. Il resta pensif quelques instants, puis reprit :
— Il y a un problème très simple à énoncer, concernant les nombres premiers, sur lequel les chercheurs n’ont pratiquement pas avancé depuis l’Antiquité.
— Voulez-vous un peu de jus de pamplemousse, demanda France, pour vous donner le courage de l’expliquer ?
— Oui, merci. Cela dit, c’est assez facile. Le point de départ consiste à remarquer qu’à part 2 et 3, deux nombres premiers ont forcément une différence au moins égale à deux…
— Je sens bien que ça doit être comme ça, mais je ne vois pas pourquoi, dit Valérie.
—Voyons, ma chérie, s’exclama France avec un rire de gorge, si deux nombres se suivent, l’un des deux est pair !
Stanislas leva sur sa femme des yeux soupçonneux. Visiblement, il n’avait pas raisonné aussi rapidement. Cela ne l’empêcha pas de ponctuer :
— C’est tranquille. Il n’y a pas d’ambiguïté.
— Bien, dit Lucien. Mais rien n’empêche deux nombres premiers d’être distants de 2, comme 3 et 5, 5 et 7, 11 et 13, 17 et 19…
— … 41 et 43, ajouta Stan.
— Exactement… On dit que deux tels nombres premiers, aussi proches que possible, sont des jumeaux. Eh bien, personne ne sait s’il existe ou non une infinité de nombres premiers jumeaux.
— Minute papillon ! s’exclama Stan très excité. Il n’y a qu’à procéder comme on a dit lundi dernier, en faisant le produit depuis 2 jusqu’à un grand nombre et en ajoutant 1, puis 3… non, plutôt -1…
— Là je suis larguée, dit Valérie en riant.
— Je te donnerai des cours de rattrapage privés, souffla Lucien, puis s’adressant à Stan : vous avez un véritable tempérament de chercheur, ma parole… C’est une idée, effectivement, mais rappelez-vous qu’en ajoutant 1,nous n’obtenions pas forcément un nombre premier, juste un nombre avec un grand facteur premier… Et c’est pareil avec -1…
— Oui, je me disais bien qu’il devait y avoir un os, répondit Stan en déballant un petit cube de fromage. Et alors, vous séchez tous là-dessus ?
— Tous les chercheurs en théorie des nombres ne travaillent pas sur les nombres premiers jumeaux, mais, oui, « nous » séchons… Il y a d’ailleurs un autre problème très voisin, posé en 1742 par le mathématicien et historien Christian Goldbach et sur lequel nous n’avons guère plus de lumières : peut-on écrire n’importe quel nombre pair comme la somme de deux nombres premiers ?
— Si l’on prend deux nombres premiers différents de 2, ce sont des nombres impairs, donc leur somme est forcément paire, remarqua Valérie…
— Oui, mais c’est le problème inverse qui intéresse les mathématiciens : donnez-moi un nombre pair…
— 1946 ! dit France en rougissant.
— Soit, répliqua Lucien. J’aurais préféré un nombre plus petit, mais on va faire avec… Val, tu as ta calculette ?
— Sûr, capitaine !
— Alors, commençons. Tu as une touche, là, qui permet de savoir si un nombre est premier.
— Celle-là, la bleue ?
— Non, juste à côté, tu vois ! On commence ? Alors 1946 – 3 = 1943. Est-il premier ?
— Non, capitaine : 1943 = 29 x 67.
— Excellent. On continue. Après 3, le nombre premier suivant est 5. Que donne la machine ?
— 1946 – 5 = 1941 = 3 x 647. Toujours pas premier…
— Ne désespérons pas, moussaillon. La manœuvre suivante est 1946 – 7 = 1939. Verdict ?
— 7 x 277, mon capitaine, toujours rien !
— Aïe, ça va être dur, mon petit. Suivant ?
— 1946 – 11 = 1935, il n’est pas premier, mon commandant.
— Comment le savez-vous, moussaillon ?
— C’est un secret de famille, mon général. J’essaie le suivant ?
— Faites, donc !
— 1946 – 13 = 1933… Oh ! Gagné, il est premier !
— Je vous fais première classe, moussaillon ! Vous voyez, 1946 = 1933 + 13 peut bien être écrit comme la somme de deux nombres premiers. Il vérifie la conjecture de Goldbach.
— Mais, il est facile votre problème, s’exclama Stan ! Il n’y a qu’à faire vérifier à un ordinateur, précisément par cette méthode, que l’on aboutit immanquablement.
— On a vérifié jusqu’à de très grands nombres, mais, tous, c’est impossible : il y a une infinité de nombres pairs…
— Alors, dans ce cas, les ordinateurs ne servent pas à grand-chose…
Stan affichait la mine du Petit Prince découvrant que les grandes personnes, qui se prétendent des gens sérieux, ne savent finalement rien de l’essentiel — vous savez, celui qui est invisible pour les yeux.
— Je me mêle peut-être de ce qui ne me regarde pas, mais…
France, apparemment enhardie par les succès de l’équipe avec le nombre 1 946, semblait prête à poser une question indiscrète. Lucien se tourna vers elle.
— Je vous en prie.
— Eh bien, voilà. Tout cela semble tout de même un peu… comment dirais-je ? un peu vain. Après tout, ça sert à quoi de savoir si les nombres premiers sont souvent jumeaux ou si M. Goldbach avait raison il y a deux cent cinquante ans ? Surtout si les réponses sont aussi difficiles à trouver ! Pourquoi dépenser une telle énergie, pourquoi vouloir à un tel prix éclairer de tels abîmes ?
Elle s’arrêta, essoufflée, étonnée de sa propre audace. Celui qui, d’une manière ou d’une autre, allait entrer dans sa famille, lui répondit doucement :
— Ces nombres que nous avons en nous font des choses plutôt bizarres. C’est vrai que nous avons envie de comprendre. Juste parce que c’est beau… comme une petite musique de nuit… Et ces propriétés correspondent précisément à une caractéristique particulière, disons « psychologique », des nombres premiers que les mathématiciens soupçonnent depuis longtemps mais qu’ils n’ont jamais réussi à mettre totalement en évidence…
— Moi, la psychologie, dit Stan, ça me dépasse encore plus que les mathématiques !
— Quelle caractéristique psychologique ? demanda Valérie, intriguée.
— Une sorte de perversion…
— Alors, là, ça commence à m’intéresser sérieusement, interrompit Stan.
— Enfin, il faut modérer tout ça, bien sûr… dit Lucien avec un sourire évanescent, mais, oui, on peut dire que les chercheurs soupçonnent que les nombres premiers sont des adeptes forcenés du principe « tout ce qui n’est pas interdit doit être essayé ».
France semblait réellement intriguée.
— Comme nos enfants quand ils étaient petits, entre deux et cinq ans… Je me souviens… De sacrés numéros : ils attrapaient tout ce qui était à leur portée et affichaient des mines étonnées quand on mettait des limites à leur capacité destructrice… Cela dit, je ne suis pas sûre de voir le lien avec vos nombres premiers.
— Ce qui frappe d’abord, quand on les étudie, c’est leur caractère apparemment aléatoire : rien ne permet a priori de prévoir si le nombre suivant sera premier ou non, enfin, pas sans des calculs précis, du genre de ceux qui permettraient de trouver tous les facteurs premiers de ce nombre ou de son suivant… Et puis, ensuite, quand on pousse l’étude un peu plus loin, on est fasciné par l’extraordinaire régularité, à grande échelle, de la suite des nombres premiers. On la met facilement en évidence avec des tables, des graphiques…
— Quel genre de régularité demanda Valérie ?
— Disons qu’on parvient à montrer que les nombres premiers se raréfient de plus en plus, mais que le pourcentage de nombres premiers dans des tranches de, par exemple, 1 000 nombres entiers consécutifs faiblit très lentement.
— C’est très abstrait pour moi, ça… dit Stan.
— Oui, effectivement, admit Lucien… Attendez je vais donner un exemple. Val, tu peux me passer ta calculette ?
— Mais certainement, très cher !
— Eh bien, voilà… un instant… Il y a 168 nombres premiers entre 1 et 1 000, 135 entre 1 001 et 2 000, 127 entre 2 001 et 3 000, 120 entre 3 001 et 4 000, etc… Ils sont de moins en moins nombreux mais il n’y pas de chute brutale de la densité de population, pas de cataclysme.
— Je ne vois aucune perversion là dedans, consigna Stan, déçu.
— Attendez… Les nombres premiers semblent donc obéir à des lois, se comporter en bons citoyens du pays des nombres. Mais, lorsqu’on les observe d’encore plus près, de nouveau, il paraissent soumis à des fluctuations très hasardeuses, comme s’ils se permettaient, et effectivement réalisaient, tout ce qui ne leur est pas explicitement interdit…
Trois paires d’yeux interrogatifs fixaient le jeune homme. Il but un verre d’eau en fermant les paupières et reprit :
— Vous, M. Million, vous avez le droit d’aller au travail en marchant sur la tête, ou de faire un détour de cinquante kilomètres le matin et trente-cinq le soir…
— Certes, ça ne tombe pas sous le coup de la loi…
— Mais pourtant, vous ne le faites pas… Dites-vous alors que les nombres premiers, c’est tout le contraire : ils font tout ce qui leur est possible.
— Par exemple ?
— Par exemple être jumeaux aussi souvent que permis. La loi de la parité leur interdit d’être distants de 1, mais ils peuvent être distants de 2, alors ils le sont, de temps en temps…
— Sauf que vous ne savez pas le démontrer ! le titilla Stan.
— Exact, pas encore, mais nous sommes sûrs que cela se passe ainsi. Dans le même genre : si un nombre n est premier, on ne peut pas espérer que n + 2 et n + 4 le soient aussi, parce que l’un de ces trois nombres est forcément divisible par 3 (pensez à 11, 13 et 15), mais rien n’interdit que n, n + 2 et n + 6 soient simultanément premiers, alors ils le sont, de temps en temps, aussi souvent que possible…
— Exemple ? souffla Valérie, visiblement prise au jeu.
— 11, 13 et 17, ou encore 41, 43 et 47, répondit Lucien du tac au tac, avec un petit sourire narquois.
— Ainsi, les nombres premiers, comme les enfants, sont des pervers polymorphes ! conclut France en riant. Est-ce que notre professeur accepterait de partager notre maigre repas ?
— Mais, je…
Lucien interrogea Valérie du regard, qui lui sourit, puis se tourna vers Stan, qui considérait sa femme, apparemment plutôt surpris par cette invitation impromptue. Le silence ne pesa pas très longtemps. Le maître de maison pivota sur son siège pour faire face au jeune homme et lança :
— À une condition, parlez-nous d’un problème de ce genre sur lequel vous autres mathématiciens, fleurons de notre civilisation savez faire quelque chose !
— Il est évident qu’un nombre premier n’est jamais un carré parfait, mais rien n’empêche le nombre qui suit un carré d’être premier, comme 5, qui suit 4, 17, qui suit 16, 37, qui suit 36, etc. Comme les nombres premiers veulent tout essayer…
— Cela arrive effectivement autant de fois qu’on veut ! Vous pouvez le prouver ?
Stan semblait enfin impressionné.
— Hélas ! Ce problème est peut-être encore plus dur que celui des nombres premiers jumeaux… Mais nous savons montrer, par exemple, qu’il existe « beaucoup » de nombres entiers n tels que le nombre entier le plus proche de …, de … attendez, je vous l’écris :
soit un nombre premier.
— Admettons, dit Stan. Cela ne justifie pas encore votre salaire, mais ça commence à ressembler à du travail… En tout cas, ça mérite bien un repas !
La soirée fut conviviale et fort détendue. Les discussions mathématiques firent naturellement place à des digressions diverses et consensuelles : vacances, tennis, planche à voile, bruit quotidien, vertus réparatrices comparées du sommeil et du calme, maison de campagne, impôts, santé, enfants. Tout au plus, le regard de Stan se figeait-il, parfois, sur Lucien, avec une forme de complicité mêlée de respect et de curiosité. Lorsqu’il partit, vers minuit, le jeune homme faisait presque partie de la famille.
Chapitre 4

Dessin : © Paul Gendrot
Ce fut donc par pure perversité que Stan demanda à Lucien de revenir une troisième fois lui parler de ses « petits problèmes ». C’était, lui avait-il confié, juste histoire d’être parfaitement convaincu.
Le dernier entretien fut programmé un jeudi férié du mois de mai. Lucien s’en serait bien passé, en fait, parce qu’il achoppait depuis plusieurs semaines sur un calcul a priori standard, et qui donnait, par deux méthodes différentes, deux résultats obstinément différents. Il était allé consulter son ancien directeur de thèse à Lyon, mais le voyage s’était révélé totalement inutile. L’ex-patron était visiblement accaparé par des préoccupations scientifiques d’un tout autre ordre : il était plongé dans un ouvrage de thermodynamique et ne parlait plus qu’entropie, potentiel, lumière et trous noirs. Lucien s’était soudain senti bien seul avec son problème. Dans le TGV du retour, il avait eu une grosse envie de tout jeter aux orties et de proposer ses services à son copain de promo Jean-René qui avait créé une boîte de services informatiques « à la carte » pour les industries lourdes — automobile et aéronautique… Cependant, au milieu de ses divagations spéculatives, une idée nouvelle lui était venue et il avait ressorti son bloc de papier blanc pour le couvrir de signes cabalistiques, excitant à son insu la curiosité de sa voisine de compartiment.
Ayant donc, indubitablement, la tête ailleurs, il fit pourtant l’effort de préparer correctement son « cours » d’un genre particulier : le sourire de Valérie valait bien cette messe.
Il était prévu qu’elle assistât son père dans cette ultime épreuve, mais elle n’était pas encore rentrée lorsque Lucien se présenta.
— Commençons sans elle, proposa Stan, visiblement conciliant. Elle prendra le train en cours de route.
— Aujourd’hui j’ai prévu de vous parler des fractales…
Le jeune chercheur avait pris de l’assurance, c’était évident.
— Vous voulez dire des fractions ? C’était un vrai cauchemar…
— Non, je dis bien des fractales, ce sont des formes géométriques un peu particulières… mais comme nous avons peu de temps, je me limiterai à une description plutôt sommaire.
— Allons-y, soupira Stan. J’espère que vos fractales seront moins perverses que vos nombres premiers… Ou au minimum moins compliquées !
— J’espère aussi, mais vous allez voir que les deux sont liés… Vous qui connaissez bien les installations de distribution d’eau, vous devez imaginer facilement le schéma de la circulation sanguine.
— Effectivement, les tuyaux, ça n’a pas de secret pour moi.
— Bien… Il y a de grosses veines, ou de grosses artères, qui se ramifient en plus petites.
— Jusqu’ici, tout va bien…
— Et ces veines ou artères se divisent elles-mêmes en veinules ou artérioles encore plus petites…
— Tant qu’on a du débit, on survit, quand on en a plus, c’est foutu…
— Imaginez alors que ce processus de division se poursuive indéfiniment. On obtient un système « circulatoire » imaginaire qui a les deux spécificités caractéristiques d’un objet fractal : d’une part, il est indéfiniment divisé, et donc totalement irrégulier, et d’autre part il est « robuste » par changement d’échelle, au sens où grossir à la loupe ou au microscope une partie du système vous ramène à une image équivalente, sinon identique au système initial.
— C’est assez monstrueux, votre engin ! Ça me rappelle les boîtes de Vache-qui-rit avec les boucles d’oreille pour vache représentant des boîtes de Vache-qui-rit, elles mêmes représentant des vaches…
Lucien sortit une feuille de papier blanc de son cartable et dessina un triangle.
— Oui, c’est l’idée. Tenez, voici un autre exemple de forme fractale facile à construire. Considérons ce triangle équilatéral et construisons des petits triangles, eux aussi équilatéraux, sur chacun des trois côtés, comme ça :

Ensuite, effaçons les base des petits triangles, pour obtenir une sorte d’étoile… Voilà.

Puis, recommençons l’opération sur chacun des nouveaux côtés de la figure obtenue…

…effaçons les traits inutiles…

Après un grand nombre d’étapes, nous obtenons une sorte de flocon de neige, tenez, je vous ai apporté une illustration trouvée sur le réseau :
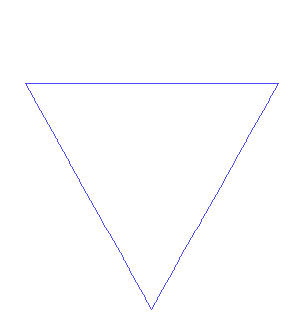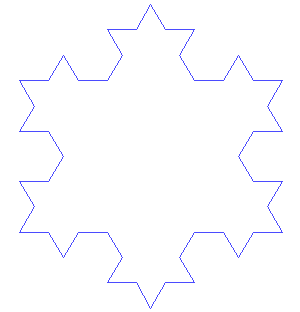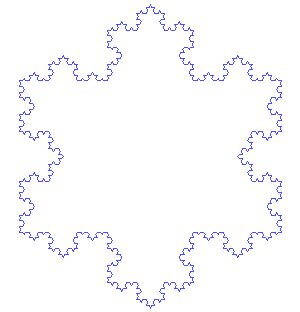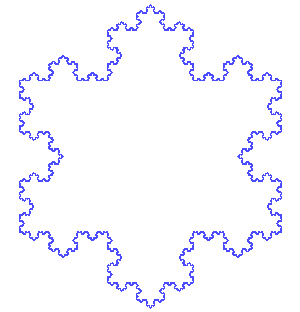
Image : António Miguel de Campos – Wikipédia.
— Plutôt joli, admit Stan.
— C’est la courbe de von Koch… Difficile de reconnaître le triangle d’origine… Mais chaque partie est semblable au tout, c’est bien une fractale !
— Et les nombres dans tout ça ?
— Ce qui est fascinant, c’est que ce sont eux aussi, en un sens, des fractales…
— Quel rapport avec les artères ou les flocons de neige ?
— Ce n’est pas si difficile à voir. Considérons un grand nombre entier tiré au hasard, avec beaucoup de facteurs premiers…
— C’est un peu difficile à se le représenter. Un exemple serait préférable, prescrit Stan.
— D’accord, attendez un peu, concilia Lucien en sortant sa calculette. Voilà, choisissons 118866.
— D’où sort-il, celui-là ?
— Ne vous inquiétez pas, il est fait pour. Sa décomposition est 2 x 3 x 11 x 1801.
— Si vous le dites…
— Cherchons alors les diviseurs de ce grand nombre. Il y a les grands et les petits…
— Et les moyens !
— Non justement, pas de moyens : un diviseur sera « grand » s’il contient le facteur premier 1801 et il sera « petit » dans le cas contraire.
— Bien vu !
— Ce n’est rien, j’ai l’habitude, je fais ça tous les soirs, rétorqua Lucien avec un petit sourire malicieux et un subtil froncement des sourcils. Bon. Reprenons. Nous avons donc deux paquets. Mais dans chaque paquet, il y a encore deux groupes…
— Ceux qui contiennent 11 et ceux qui ne le contiennent pas ! s’exclama Stan, très satisfait de lui-même.
— Exact !
— Et ainsi de suite, avec 3 puis enfin 2…
— C’est ce qui fait de ce nombre une sorte de fractale : deux paquets, puis dans chaque paquet, deux nouveaux paquets, etc.
— Oui… je vois…
Stan avait les yeux dans le vague, voire du vague dans les yeux.
C’est à cet instant que Valérie entra. Leste, élégante, fraîche. Elle embrassa son père et, du plat de la main, souffla un baiser vers Lucien, ostensiblement déçu.
— Alors, papa, qu’as-tu appris de nouveau aujourd’hui ?
— Qu’un nombre entier pris au hasard ressemble à un flocon de neige… C’est fou, tout de même ! Se retournant vers Lucien il ajouta : mais enfin, tous les nombres ne sont quand même pas comme ça, c’est trop fort !
— Non, bien sûr, mais on sait, et c’est une découverte assez récente, qu’ils sont « presque tous » fabriqués sur le même modèle…
— Presque tous ?
— Disons que si vous les tirez au hasard sur des billets de loterie, vous avez de très grandes chances de tomber sur un flocon plutôt que sur un nombre bien lisse…
— Dommage que je n’aie pas vu le début du film, je suis totalement larguée, dit Valérie. Et l’assassin, c’est qui ?
— Le hasard, comme d’habitude, répliqua Lucien, presque sérieux.
— Allez… Tu peux me résumer les chapitres précédents ? supplia Valérie avec une petite voix.
— Je vais faire mieux, dit Lucien, tu vas voir… Tout à l’heure nous avons analysé la structure du nombre 118866, dont les facteurs premiers sont 2, 3, 11, 1801. Rangeons ses seize diviseurs dans l’ordre croissant : nous obtenons
1, 2, 3, 6 = 3 × 2, 11, 22 = 11 × 2, 33 = 11 × 3,
66 = 11 × 3 × 2, 1801, 3602 = 1801 × 2, 5403 = 1801 × 3,
10806 = 1801 × 3 × 2, 19811 = 1801 × 11,
39622 = 1801 × 11 × 2, 59433 = 1801 × 11 × 3
118866 = 1801 × 11 × 3 × 2.
— Bravo ! s’exclama Valérie, mais, moi ça ne me parle pas franchement du côté du vécu…
— Attends… On va maintenant faire un petit tour de passe-passe. On remplace 1 par a, 2 par b, 3 par c, 11 par d, 1801 par e, et on réécrit la même liste avec les lettres à la place des chiffres.
— Si ça peut te faire plaisir…
— Regarde, on obtient
a, b, c, cb, d, db, dc, dcb, e, eb, ec, ecb, ed, edb, edc, edcb.
— Mouais, dit Valérie, et alors ?
— Tu ne vois rien ?
— Non… et toi, papa ?
— Papa ne voit rien non plus, éructa Stanislas Million.
À cet instant, France entra dans la pièce, un plateau de boissons dans les mains. Elle jeta un coup d’œil à la feuille posée sur la table basse, que son mari et sa fille scrutaient désespérément.
— Tiens, dit-elle, c’est rangé comme dans un dictionnaire !
— Bravo, Mme Million, c’est vous la meilleure !
Lucien essuya prestement son front du revers de sa manche et sourit à la ronde d’un air victorieux.
— Je ne voudrais pas te contrarier, mon chéri, dit doucement Valérie, mais il n’y a pas de quoi pavoiser…
— Disons que c’est une propriété remarquable…
— Et presque tous les nombres sont comme ça, rangés alphabétiquement ? demanda Stan.
— Non… C’est un peu plus compliqué… En fait, presque aucun nombre n’est strictement rangé de cette façon. Mais presque tous le sont « presque », ce qui ne perturbe pas la structure fractale…
— Ils aimeraient bien jouer au dictionnaire, mais ils font des petites erreurs d’ordre alphabétique, quoi ! résuma Stan.
— On peut le dire comme ça, convint Lucien.
— Pas mal quand même, admit Stan, rêveur…
— Merci… Nous y sommes donc arrivés, dit Lucien. Après un instant d’hésitation et une courte inspiration, il ajouta :
— Et si je vous invitais tous au restau ?
La plupart des sujets abordés dans le texte précédent correspondent à des sujets de recherche de l’équipe de théorie (analytique) des nombres de l’institut Élie Cartan, au sein de l’Université Nancy 1 :
- Jie Wu a travaillé sur les nombres premiers jumeaux. En collaboration avec Joël Rivat, il a trouvé des nombres premiers proches de nc avec c = 1,18.
- Joël Rivat et Patrick Sargos ont, pour leur part, établi qu’avec une valeur un tout petit peu plus faible de c, les nombres premiers en question surgissent avec la régularité attendue.
- Cécile Dartyge s’est penchée sur le problème si difficile des nombres premiers de la forme n2 + 1.
- André Stef et l’auteur de ces lignes ont partiellement percé les secrets des nombres « lexicographiques », dont les diviseurs sont rangés par ordre alphabétique.
- En collaboration avec Michel Mendès France, de l’université de Bordeaux, le signataire a décrit la structure fractale des diviseurs. Les mêmes ont également commis un volume de la collection Que sais-je ? sur les nombres premiers…
Ce texte a été publié une première fois en octobre 2003 dans le numéro hors série de la Revue de l’Institut Élie Cartan 1903 – 2003 Un siècle de mathématiques à Nancy.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Gérald Tenenbaum