
Une histoire de la modélisation des plantes
Aujourd’hui, la botanique se sert des outils informatiques pour comprendre, simuler et prévoir le développement des plantes et le fonctionnement des écosystèmes, en interaction avec leur environnement. Mais qu’en était-il autrefois ?
1. Une brève histoire de l’étude des plantes

Jardin botanique de Montpellier.
Photo : Koakoo
Nous devons aux plantes notre oxygène, notre nourriture, notre santé, notre mobilier, notre habillement et l’agrément de notre environnement naturel extérieur et intérieur, c’est dire assez leur importance et leur utilité. L’usage des plantes accompagne l’histoire de l’humanité, qui a développé d’abord la cueillette puis l’agriculture et parallèlement a découvert les vertus des plantes médicinales. Il a fallu identifier et sélectionner les espèces, choisir les organes utiles à la consommation et définir les modes de culture. Plusieurs siècles avant notre ère, les Chinois ont laissé des ouvrages d’arboriculture très complets parlant de greffage, de bouturage et de marcottage.
La découverte de nouvelles sources de nourriture, d’épices, de médicaments ou de nouveaux matériaux utiles comme le caoutchouc, a constitué un enjeu majeur des grandes expéditions maritimes des siècles précédents qui comportaient toujours des botanistes. Afin de classer et répertorier l’arrivée massive des nouvelles espèces découvertes, la botanique a développé progressivement les critères de la classification végétale. La création de jardins botaniques a permis de conserver et de reproduire les espèces utiles à l’homme. Celui de Montpellier, le plus vieux de France, a ainsi fêté ses 400 ans !
Une généalogie de la botanique…
L’étude de l’anatomie des plantes, qui a donné la botanique, est très ancienne. On connaît par Théophraste (vers 300 av. J.-C.) les principes de la classification des végétaux en arbres, arbrisseaux et herbes établie par son maître Aristote. Le médecin romain Dioscoride (Ier siècle) publie le livre De materia medica où sont décrites et dessinées 600 plantes avec leurs propriétés médicinales.
Au XVIIe siècle, le Français Joseph Pitton de Tournefort (1656-1708) construit à partir de ses voyages en Europe un herbier qui figure toujours au Muséum. Il publie Les éléments de Botanique en trois volumes illustrés par le peintre Aubriet, complétés par les Institutiones rei herbariæ, œuvre qui marque l’histoire de la botanique. Il distingue les apétales, les monopétales et les polypétales. Il utilise la notion de genre et de familles (labiées, crucifères, ombellifères…) qui sera conservée par Linné au XVIIIe siècle.
Pour Linné (1707-1778), la classification est le fait du raisonnement et n’est pas objective comme résultant de l’œuvre de la nature. Il a écrit de nombreux ouvrages dont Systema naturae (1735) et Philosophia botanica (1751). Il organise la classification des plantes selon la description des fleurs. Vingt quatre classes sont reconnues et divisées en ordres. Il préconise de nommer tous les êtres vivants par un substantif qui est le genre et un adjectif qui est l’espèce, ce qui a été définitivement adopté.
La famille de Jussieu comprend cinq botanistes. Antoine Laurent de Jussieu (1748-1836) montre qu’il faut être moins rigide sur la classification à base de l’organisation des fleurs, mais qu’il faut tenir compte de tout un ensemble de caractères botaniques pour définir les liens de parenté qui désignent une famille naturelle. Il expose son principe dans le Genera plantarum en 1789. Il distingue cent familles et les combine avec les notions de genre et d’espèce et de structure des graines.
L’écrivain Goethe (1749-1832), passionné de botanique, est l’inventeur du mot morphologie et découvre la métamorphose végétale qu’il publie dans son livre La métamorphose des plantes (1790). Il pense que la fleur est le prolongement de la spirale génératrice qui dispose les feuilles le long des axes, feuilles qui se transforment progressivement en sépales, pétales et étamines.
…et de l’agronomie
L’agronomie en tant que science se développe au XVIIe siècle. Olivier de Serres (1539-1619) publie son Théâtre de l’Agriculture dans lequel il indique les méthodes de labour, de fumures et d’ensemencements ainsi que les procédés de greffage et de taille des arbres fruitiers.
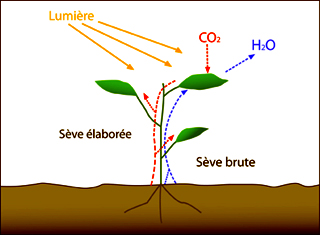
La photosynthèse est l’un des processus biogéochimiques les plus importants de la nature. Grâce à l’énergie solaire, les végétaux vont pouvoir transformer l’eau (H2O) du sol et le gaz carbonique de l’air (CO2) en substances organiques. Ils rejettent de l’oxygène (O2) et produisent des sucres (le glucose, C6H12O6) indispensables à leur croissance.
Jean-Baptiste de la Quintinie (1624 ou 1626-1688) fut le responsable du potager du roi à Versailles. Son Introduction pour les jardins fruitiers et potagers (1690) très bien illustrée eut un bon succès. Sa méthode de taille plus sévère qui augmente significativement la production fruitière a été abondamment diffusée et utilisée.
Au XIXe siècle, Théodore de Saussure est le père de l’agronomie. Il publie en 1804 ses Recherches chimiques sur la végétation. Dans cet ouvrage, il démontre que tout le carbone des plantes provient de l’air, que l’eau du sol fournit une partie de l’oxygène. Il prouve aussi que l’azote contenu dans la plante provient du sol et non de l’air. Il reconnaît au terreau son pouvoir fertilisant par les sels qu’il contient même à un faible taux de dissolution. Saussure a clarifié définitivement les problèmes liés à la nutrition, tant en ce qui concerne le rôle des organes (feuilles, racines) que celui des constituants majeurs de l’architecture végétale.
Julius von Sachs (1832-1897) établit clairement le fonctionnement respiratoire et photosynthétique des plantes. Il montre que la respiration s’accompagne de la destruction des hydrates de carbone et que la synthèse de l’amidon provient de l’activité chlorophyllienne. Il établit l’équation fameuse :
6 CO2 + 6 H2O + ÉNERGIE SOLAIRE = C6H12O6 + 6 O2
En 1892, Joseph Anton Boehm permet d’expliquer l’ascension de la sève brute dans les grands arbres. L’eau évaporée à la surface des feuilles est immédiatement remplacée par celle qui provient des canaux à l’intérieur du système ramifié.
Botanique et physiologie végétale deviennent alors deux concepts séparés, le premier s’occupant de la classification et le deuxième du fonctionnement des plantes.
Vers la constitution de modèles en biologie
Les mécanismes physiologiques du fonctionnement végétal au niveau cellulaire et moléculaire seront identifiés au XXe siècle. Contrairement à la physique, la biologie n’a pas engendré beaucoup de modèles mathématiques, et encore, ceux-ci sont apparus avec deux siècles de retard. Seuls les modèles de la génétique initiés par Mendel puis développés par Morgan ont pris le statut de modèles mathématiques en constituant la génétique quantitative.
La biologie était donc avant tout affaire d’érudition, plutôt qu’affaire de calculs. Les physiciens ont pu, en observant l’échelle macroscopique, tirer des concepts quantitatifs efficaces qui leur ont permis, tout en ignorant la structure atomique, de formuler des lois et de bâtir des modèles au fur et à mesure de l’avancée parallèle des mathématiques. Ainsi, les concepts de masse, de volume, de pression et de température ont permis à Mariotte de trouver les lois des gaz deux siècles avant leurs justifications théoriques au niveau moléculaire par Boltzmann.
La mécanique, l’optique, l’électricité, ont toutes eu pareillement leurs approches macroscopiques, bien avant la découverte de l’atome, avec l’efficacité que l’on sait sur le formidable développement des sciences et techniques. La biologie végétale a sauté cette étape. Paradoxalement, elle est parvenue au XXe siècle à mieux connaître la biophysique et la biochimie du fonctionnement des êtres vivants, c’est-à-dire les aspects quantitatifs du niveau microscopique, que les lois macroscopiques du fonctionnement de la plante au niveau de son architecture.
Bien que les lois observées à un niveau donné soient nécessairement déterminées par celles des niveaux inférieurs, elles ne peuvent s’en déduire facilement et à l’instar de la physique, il convient de raisonner à l’échelle concernée. Ce n’est que récemment, à la fin du XXe siècle, qu’a vraiment commencé la modélisation de la croissance des plantes avec l’architecture comme support du fonctionnement. Elle est le résultat de trois approches séparées qui ont progressivement convergé : les modèles de la botanique, les modèles de l’agronomie et les modèles géométriques de l’informatique. Bien que l’informatique ait été un instrument déterminant dans la génération des modèles d’architecture végétale, les équations de ces modèles auraient très bien pu être trouvées au XIXe siècle.
Les modèles de l’architecture des plantes en botanique
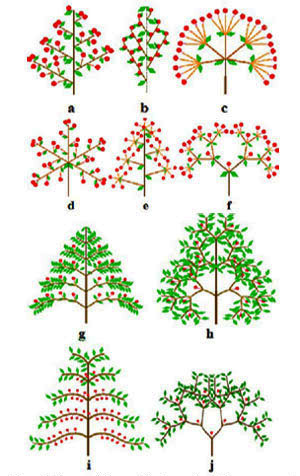
Les modèles architecturaux des inflorescences et des arbres tropicaux.
Inflorescences : (a) grappe de grappe,
(b) épis,
(c) ombelle d’ombellules,
(d) ombelle de grappes,
(e) grappe d’ombellules,
(f) cyme bipare.
Arbres (modèles selon F. Hallé et R. Oldeman) :
(g) modèle de Fagerlind (ex : Magnolia),
(h) modèle de Scaronne (ex : manguier),
(i) modèle de Massart (ex : araucaria),
(j) modèle de Leeuwenberg (ex : frangipanier).
Une pure combinatoire assemble en arborescences les modes de croissance, de ramification et de floraison. La nature exprime une bonne partie des possibilités, mais pas toutes…
La floraison des végétaux a attiré très tôt l’attention des botanistes et fait l’objet d’études détaillées : cymes, corymbes, ombelles, grappes et leurs combinaisons, correspondent à autant de possibilités combinatoires d’inflorescences que l’on retrouve dans toutes les espèces. Les botanistes de l’ORSTOM Francis Hallé et Roelof Oldeman ont réussi en 1970 à étendre aux architectures végétales des arbres le principe de la classification des inflorescences. Pour cela, ils se sont basés sur une combinatoire liant la croissance continue ou rythmique des méristèmes (bourgeons), la floraison latérale ou terminale des axes et leurs types de différenciation, que l’on appelle encore âge physiologique et dont Goethe a été un précurseur. Un même type d’axe peut se retrouver à différents endroits au sein d’une architecture, même taillée abondamment comme c’est le cas des arbres fruitiers. Ainsi sont nés les modèles architecturaux, dessins de botanistes qui classent en moins de trente catégories les arbres de toutes les espèces connues. L’architecture est ici considérée non pas d’une manière statique, à l’instar des planches botaniques qui décrivent seulement minutieusement les parties de la plante, mais comme le résultat de l’organogenèse des méristèmes, qui caractérise la cinétique de la mise en place des axes feuillés d’un arbre, plus simplement appelée son développement.
Les modèles de la production végétale en agronomie
Parallèlement et au même moment (dans les années 1970), mais sur un tout autre registre, l’agronomie s’est intéressée à la prédiction de la production végétale calculée au niveau du mètre carré, en fonction des paramètres environnementaux (lumière, température, eau, azote…). Cette production est exprimée en matière sèche, après dessiccation de la matière fraîche dans une proportion d’environ 10 %.
La plante n’est plus considérée individuellement, ce qui compte ici c’est la surface foliaire par mètre carré (ou LAI, pour Leaf Area Index, Indice de surface foliaire), et la production végétale par mètre carré, qui est généralement divisée en compartiments (feuilles, entre-nœuds, fruits, racines.) Tous ces compartiments se partagent la quantité disponible de biomasse, dans laquelle ils puisent chacun selon sa propre force, appelée force de puits. À ce niveau macroscopique, les agronomes ont montré que la production était étroitement liée à l’énergie utile de la lumière incidente (le PAR), à la lumière interceptée par le couvert et à un facteur de proportionnalité qui est l’efficience de la lumière (la LUE). Les Hollandais ont été les pionniers de cette approche de la production végétale, dont la paternité revient à De Witt dans les années 1970.
Ainsi dans une serre hollandaise en été, le PAR incident qui arrive sur le couvert dans la serre après avoir traversé les vitres vaut 6 Méga Joule/m2/jour et la LUE 3 g/MJPAR. L’interception de la lumière est modélisée par la loi de Beer-Lambert :
I = (1-exp(-k.LAI)) (équation 1) ;
où k est un coefficient empirique dépendant des propriétés du couvert qui vaut environ 0.7 en moyenne.
Finalement, la production d’un mètre carré de culture est donnée par la formule :
Q = LUE × PAR × (1 – exp(-k.LAI)) (équation 2).
Si la surface foliaire par m2 devient supérieure à 4, la lumière est entièrement interceptée et I = 1. La production au m2 est alors saturée et on ne peut guère dépasser une production en matière sèche supérieure à 20 grammes par mètre carré par jour, ce qui exprime clairement la contrainte d’une limitation de la production. En conséquence, l’augmentation de la densité ne sert à rien si la surface foliaire par mètre carré est supérieure à 4.
Une autre loi empirique remarquable à l’échelle de la plante est la notion de temps thermique. Il correspond à la somme des températures moyennes journalières reçues par le couvert. Le développement végétal est très instable si on considère le temps calendaire, la plante pousse et ralentit par paliers. Mais si on utilise le temps thermique, on peut établir des relations linéaires. Il faut en effet un certain cumul thermique pour déclencher, au-delà d’un seuil, la levée des semences, le rythme d’émission des feuilles par les méristèmes, la mise à fleur… Le temps thermique pilote les séquences du développement végétal et il remplace souvent le temps calendaire dans les modèles de l’agronomie.
2. La botanique du XXIe siècle : les modèles structures-fonction pour la simulation informatique
L’arrivée des ordinateurs a révolutionné les méthodes de modélisation et de simulation des systèmes. L’étude des plantes en a bien sûr profité. Deux tendances ont émergé, qui sont détaillées ci-dessous. L’une est basée sur la simulation informatique de plus en plus fine du fonctionnement, c’est le cas notamment des L_systems, l’autre s’appuie sur les méthodes de l’automatique en utilisant des systèmes dynamiques, tout en gardant les simplifications judicieuses des modèles agronomiques comme l’efficience de la lumière (LUE) et le partage de la biomasse commune, mais en l’adaptant au niveau de l’organe.
Tendances en simulation informatique de la croissance des plantes
Les ordinateurs ont fait leur apparition en même temps que les modèles de la botanique et de l’agronomie. L’augmentation progressive de leur capacité de calcul et l’arrivée de l’image de synthèse, grâce aux écrans graphiques, ont permis aux informaticiens de s’attaquer aux phénomènes naturels comme la croissance des plantes. La complexité géométrique des arbres avait tout pour plaire aux informaticiens qui ont recherché des algorithmes puissants pour simuler l’architecture végétale d’une façon purement géométrique : arbres combinatoires, binaires, fractals ont ainsi vu le jour. Mais ces outils demeuraient trop rigides pour simuler le développement complexe des plantes.
C’est alors qu’Aristid Lindenmayer, botaniste informaticien hollandais, a conçu un système de réécriture au formalisme très puissant (les grammaires de Lindenmayer aussi appelées L_systems) capables de reproduire le développement des méristèmes dans leurs ramifications et leurs différenciations. L’approche convient particulièrement aux plantes herbacées, dont la grammaire de développement reste simple à identifier empiriquement. À l’Université de Calgary, le professeur P. Prusinkiewicz a développé une plate-forme informatique (L_studio) autour des L_systems qui a rendu de grands services aux écophysiologistes, leur permettant de reconstruire leur plante, (par exemple les modèles ADEL de l’INRA pour le maïs et le blé, ADEL-maïs et ADEL-blé).
Ces modèles L_systems de plantes ont d’abord été basés sur le couplage du temps thermique avec la production et l’expansion des organes vue sous un angle purement géométrique. La plante pousse grâce au fonctionnement des méristèmes et à la dilatation forcée des organes créés qui est pilotée par le temps thermique. Mais elle ne fonctionne pas vraiment car il n’ y a pas de biomasse synthétisée. La simulation informatique donne une maquette 3D aussi fidèle que possible, utilisée notamment pour les calculs d’interception de la lumière et le calcul des micro-climats qui environnent les feuilles. L’utilisation du temps thermique pour établir l’architecture suppose que l’environnement lumineux est stabilisé, ce qui est souvent le cas pour les cultures de printemps, mais pas pour les cultures d’hiver.
Aujourd’hui, les écophysiologistes s’efforcent d’intégrer de façon fine le fonctionnement de la plante en introduisant des mécanismes de plus en plus précis. La photosynthèse est calculée au niveau de chaque feuille en fonction de son micro-climat et les sucres synthétisés sont redistribués dans l’architecture de la plante par un système de transport – résistance, selon la force de puits d’attraction des différents organes.
Les implémentations de tels systèmes complexes (citons AMAP Hydro, Lignum, Vica, Gro-IMP, L_peach, Graal), entièrement basés sur la simulation, permettent une bonne capitalisation des connaissances, mais ne permettent pas d’aborder le calcul de la production végétale d’un peuplement, pour plusieurs raisons. Les temps de simulations et leurs ressources de calcul à mobiliser (la mémoire par exemple) sont généralement trop conséquents. Le nombre important de paramètres à identifier ne permet pas commodément la méthode inverse, indispensable pour caler le modèle en conditions réelles.
Les L_systems ont, jusqu’à présent, produit des simulations, mais ils n’intègrent pas les équations de production qui devraient s’en déduire. Ce qui fait que ces simulations perdent en efficacité et ne peuvent pas aborder correctement les grandes structures comme les arbres, ni les problèmes inverses, le contrôle et l’optimisation.
Un modèle de l’automatique pour la croissance des plantes : GreenLab
Aborder ce problème avec une approche de l’automatique, c’est l’objet du modèle GreenLab, développé par l’équipe de recherche Digiplante en France et au LIAMA en Chine, par filiation des modèles de plantes de l’AMAP du CIRAD. Un automate (qui s’écrit également sous forme d’une grammaire récursive) modélise le fonctionnement des bourgeons en contrôlant leurs productions et leurs différentiations, qui dépendent de la notion d’âge physiologique. Il permet de factoriser le développement de l’architecture.
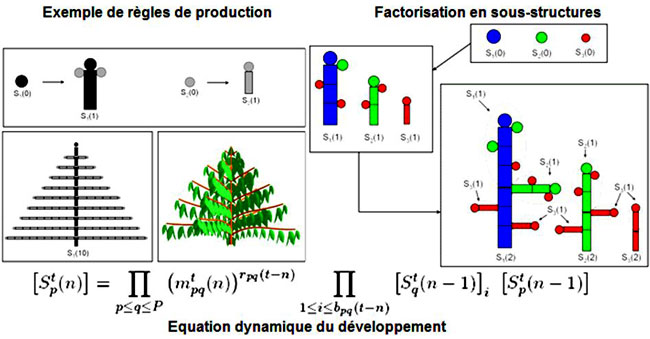
Le fonctionnement des bourgeons peut être modélisé par un automate dont les états correspondent aux différents âges physiologiques identifiés dans la plante. Les transitions entre les états se font soit par la ramification, soit par une mutation. La grammaire associée à l’automate (voir la formule dans cette figure) permet une puissante factorisation du développement de la plante.
De ce fait, le temps de calcul n’est plus proportionnel au nombre d’organes produits (comme en simulation), mais seulement proportionnel à l’âge de la plante. Sous sa forme stochastique, l’automate permet d’obtenir directement les moyennes et les variances de ces nombres d’organes. En particulier, une fonction de production déduite de la grammaire de GreenLab donne le nombre d’organes associés à chaque cohorte qui se met en place. En multipliant chaque nombre d’organes ainsi obtenu par la force de puits des organes correspondants, puis en additionnant les résultats, on obtient la demande de la plante. L’accès rapide à l’estimation de cette dernière est un atout important dans le calcul de la production de la plante.
Les organes sont en compétition pour les ressources qui assurent leur expansion. Ils se partagent un pool commun en fonction de leurs forces de puits. L’expansion d’un organe au cours d’un cycle de croissance s’écrit :
Δq = p Q / D (équation 3) ;
où p est sa force de puits, Q la ressource disponible à se partager et D la demande de la plante. Comme expliqué ci-dessus, la demande de la plante est la somme de tous ses puits actifs, c’est une fonction de production déduite de la grammaire de GreenLab. En additionnant le poids des feuilles et en divisant par leur épaisseur, on calcule la surface foliaire active S, ce qui donne le LAI et donc la nouvelle biomasse produite grâce à la formule (2). La récurrence du système est donc bouclée et la croissance de la plante peut alors se calculer de cycle en cycle à partir de la graine, en fonction des échanges sources-puits.
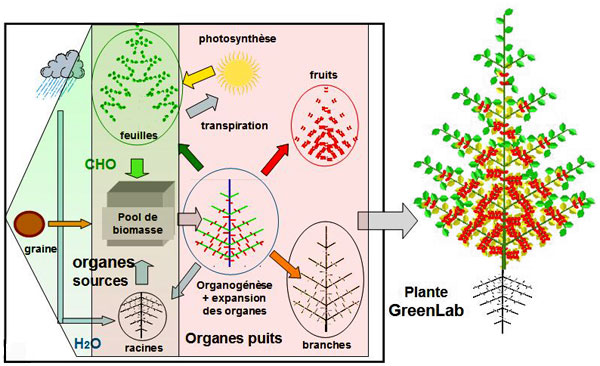
Schéma du développement et de la croissance des plantes en fonction de leur environnement mis en œuvre dans le modèle GreenLab. L’eau et le gaz carbonique assurent 95 % de la biomasse fraîche végétale. Les bourgeons utilisent la biomasse synthétisée par les feuilles pour fabriquer les nouveaux organes qui peuvent être des sources (graines), des sources-puits (feuilles) ou des puits (fruits, racines, branches).
© Digiplante, Greenlab.
L’identification des paramètres du modèle sur les plantes réelles, par la méthode inverse, est un enjeu important, car ces paramètres sont des composantes du rendement utilisables par la suite en génétique, ou en optimisation des itinéraires culturaux (irrigation, densité). Un point fort du modèle GreenLab réside justement dans l’application de la méthode inverse. Avec ses différents partenaires (INRA, CAU, Wageningen, ITB…), l’équipe Digiplante a commencé à calibrer les espèces cultivées. La simulation du modèle à partir des paramètres mesurés sur les plantes permet de calculer leur production et de restituer en 3D leur architecture.

Simulations par le logiciel Digiplante (ECP) de plantes cultivées dans le cadre de collaborations avec des laboratoires de différentes institutions. Les architectures sont construites à partir des paramètres du modèle GreenLab estimés par méthode inverse, sur des plantes réelles.
(a) betterave (ITB), (b) arabidopsis (Lepse Inra), (c) blé (University of Wageningen UW), (d) riz (Chinese Agriculture University CAU), (e) maïs (CAU), (f) tournesol (Lepse Inra), (g) chrysanthème (UW), (h) concombre (CAU), (i) tomate (CAU), (j) poivron (UW), (k) caféier (Vietnam), (l) pin (Chinese University of Forestry – CAF).
© Digiplante.
La plasticité de l’architecture des plantes
L’architecture d’une plante résulte de la création des organes par les méristèmes, de leur expansion et de leur mise en place dans la structure tridimensionnelle. Ces phénomènes sont fortement contrôlés par les paramètres climatiques (température, lumière, eau) et généralement, ils interagissent entre eux par rétroaction. Ces interactions génèrent une forte plasticité au niveau de l’architecture végétale.
On peut distinguer deux types principaux de plasticité selon qu’on considère les herbacées ou les arbres :
- Chez les herbacées, le schéma de développement est en général stable, la grammaire associée au fonctionnement des méristèmes est quasi déterministe (la structure des inflorescences est très régulière), mais l’expansion des organes est totalement décalée par rapport au schéma de leur mise en place. Selon le stress, l’expansion des méristèmes axillaires sera plus ou moins inhibée. Les lois de retard à l’expansion des ramifications peuvent être basipète ou acropète. Dans le cas extrême, seule la tige principale est construite, les ordres de branchements successifs ne peuvent se manifester qu’en fonction de la diminution du stress. Le logiciel GreenScilab développé au Liama est bien adapté au cas de la simulation de la croissance des herbacées.
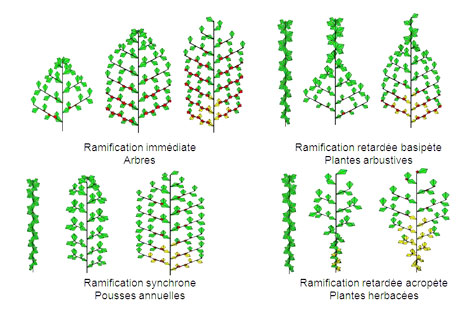
Divers schémas d’expansion des organes associés à un même schéma de développement chez les plantes. Une même organogénèse produite dans les bourgeons peut donner lieu à des types de croissance différente.
Images : d’après Kang MengZhen, LIAMA, logiciel GreenScilab. - Chez les arbres, le schéma de développement peut être fortement perturbé, mais la croissance des organes suit en général leur mise en place par les méristèmes. Développement et croissance sont donc liés. Le fonctionnement des méristèmes dépend fortement du rapport au sein de la plante entre la ressource disponible et la demande. Cela touche la longueur des pousses, le nombre et la durée de vie des branches. Ainsi un hêtre de 15 ans peut mesurer 15 m ou 15 cm de hauteur selon qu’il ait poussé au soleil ou à l’ombre ! Dans le dernier cas, l’arbre qui est une sorte de « bonzaï » ne ramifie pas et fait une pousse annuelle qui n’a que deux feuilles. Le logiciel Digiplante développé à l’École Centrale est bien adapté au cas des arbres et permet d’étudier les interactions croissance – développement.
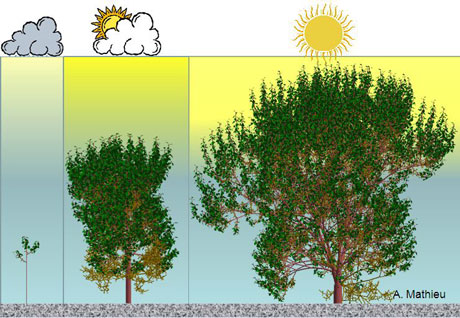
Différentes expressions phénotypiques d’un même génotype d’arbre au même âge (15 ans), dans des conditions environnementales de lumière différentes. L’arbre à l’ombre ramifie peu et fait des pousses courtes; l’arbre en plein soleil, ramifie abondamment et fait des pousses longues. Cette plasticité est le résultat des interactions croissance développement au niveau des pousses produites par les méristèmes.
Images : d’après Amélie Mathieu, ECP, logiciel Digiplante.
Le schéma de développement provenant de la grammaire qui contrôle le fonctionnement des méristèmes peut être affecté fortement en cas de stress. Ainsi, le nombre de feuilles fabriquées dans une pousse annuelle, la ramification qui se met en place ou les taux d’avortements peuvent être fortement modifiés. Par ailleurs, la forme géométrique des organes peut également changer. À l’ombre, les entre-nœuds ont tendance à s’allonger et les feuilles à être plus fines. Notons que les phénomènes aléatoires qui touchent la croissance, la ramification et la mortalité des méristèmes — et qui sont pris en compte dans le modèle GreenLab quand c’est nécessaire — ne changent pas globalement le schéma de développement, mais ont seulement un effet localisé dans l’architecture.
3. Visualisation des plantes en images de synthèse
L’histoire de la visualisation des plantes est directement liée aux progrès des ordinateurs et de l’image de synthèse. En France, il y a vingt ans, l’informaticien Jean Françon a été un pionnier dans ce domaine. Les premiers dessins ont été effectués par des traceurs de courbes ! Les premiers écrans graphiques étaient vectoriels et directement issus des oscilloscopes. Les écrans graphiques spécialisés, travaillant au niveau du pixel, sont apparus avec des cartes spécialisées de plus en plus performantes. Un arbre dessiné au traceur de courbe pouvait prendre une dizaine d’heures, le même avec des polygones coloriés sur un ordinateur doté d’une bonne carte graphique ne prendra que quelques millisecondes.
|
|
| Simulation de l’architecture des arbres : tracé du modèle de Massart, suivi d’autres modèles. Film réalisé à l’occasion de la thèse de Philippe de Reffye, 1979. Durée : 2 min 49 s – muet. |
La visualisation de l’architecture des plantes
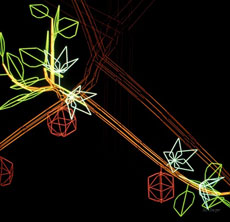 |
 |
| Premiers modèles 3D d’arbres simulés par le logiciel AMAP en 1985 : photographies d’écrans. À gauche, détail de modèle de Leewenberg sur station vectorielle PS300 de Evans et Sutherland (IBMC Strasbourg). À droite, détail de palmier sur station de travail Tektronix 256 (CNRS Cronenbourg Strasbourg). Images © Marc Jaeger. |
|
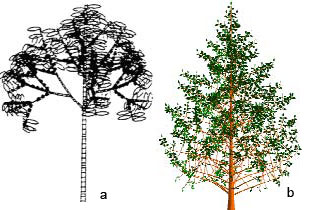
Dessins d’arbres sur ordinateur :
(a) dessin par un traceur de courbe d’un arbre piloté par un calculateur HP 9825. (Thèse de Ph. De Reffye, 1979).
(b) construction d’un arbre par le logiciel Digiplante.
Si les règles géométriques n’ont pas beaucoup changé, le nombre de paramètres du fonctionnement pris en compte a beaucoup augmenté. L’arbre (a) ne prend en compte que le développement et la géométrie, l’arbre (b) intègre les relations sources-puits dans l’édification de son architecture.
La construction 3D d’une plante se fait en couplant des règles géométriques à la production du développement par l’automate. Ces règles positionnent correctement dans l’architecture les organes dont la forme est connue et le volume calculé à partir de son expansion donnée par l’équation (3). Elles concernent l’empilement des entre-nœuds pour produire un axe, la phyllotaxie pour disposer correctement les organes autour de la tige, l’angle de branchement et la courbure des axes… Toutes les données concernant la géométrie sont mesurables et sont des paramètres d’entrée pour la simulation de l’architecture. Dans le modèle GreenLab, l’architecture de la plante est une sortie optionnelle de la simulation. En général, le calcul de la production de la plante ne nécessite pas la définition géométrique de la structure, mais seulement de son développement et des relations sources-puits, ce qui fait gagner beaucoup de temps de calcul.
La simulation de paysages en image de synthèse
L’image de synthèse est maintenant couramment utilisée pour simuler les scènes d’urbanisme et de paysagisme avec un grand réalisme. Des sociétés sont spécialisées dans la fourniture de végétaux virtuels pour les besoins de l’image de synthèse, par exemple Bionatics. Une application inattendue est la visualisation, qui se veut réaliste, d’un paysage du Carbonifère avec des plantes, construite par le logiciel AMAP du Cirad en collaboration avec les paléobotanistes de Montpellier.

Simulation d’un paysage paléobotanique avec des calamites, des sigillaires et des lépidodendrons.
Image calculée par R. Lecoustre, logiciel AMAP du Cirad.
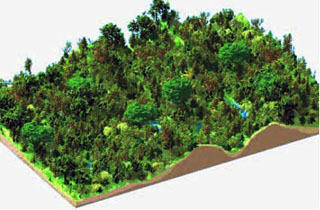
Un paysage fonctionnel.
Les plantes occupent un volume divisé en petits cubes qui contiennent l’information issue de la simulation. © Marc Jaeger (INRIA-Cirad)
Les paysages fonctionnels sont les derniers avatars des peuplements virtuels. Dans ceux-ci, une information à la fois quantitative et qualitative est disponible. Les plantes poussent dans un environnement radiatif pour la partie aérienne et hydrique pour la partie souterraine. Au-delà de la visualisation de l’image, on a accès sous forme de coupes analogues à celles d’un scanner à la quantité de biomasse produite à la surface foliaire. Les techniques de l’analyse d’image permettent d’analyser le peuplement simulé et d’estimer par exemple la production végétale pour différents compartiments.

Image de synthèse de paysage.
Ici les plantes simulées sont purement géométriques et ont pour but d’être utilisée dans les projets d’architecture et de paysagisme pour compléter le bâti. Les connaissances requises sont botaniques et informatiques.(Bibliothèque de plantes et logiciel AMAP de croissance de plantes – Image créée par Bionatics.)

Visualisation d’un paysage fonctionnel.
Les arbres de ce bois, simulés par le modèle GreenLab, ont poussé en utilisant les ressources de l’environnement. Pour chaque arbre, la photosynthèse est calculée à chaque cycle de croissance en estimant la lumière interceptée, et la biomasse fabriquée sert à construire l’architecture. La compétition entre arbres est prise en compte. On peut donc connaitre théoriquement la production à l’hectare d’une culture, l’eau évaporée… Les connaissances requises sont botaniques, agronomiques et informatiques. (Images UMR AMAP Cirad – équipe-projet Digiplante INRIA).
Conclusion
Grâce à la modélisation mathématique, l’architecture et le fonctionnement des plantes peuvent être mis en équation. Les paramètres de ces modèles extraits des plantes cultivées, en tant que composantes essentielles du rendement, devraient être des indicateurs utiles pour la sélection végétale et l’optimisation des itinéraires culturaux en agronomie. Parallèlement, grâce aussi à la puissance acquise par les micro-ordinateurs, la simulation des paysages où les plantes virtuelles jouent un grand rôle devient un outil couramment utilisé par les architectes-paysagistes.
Une première version de ce texte a été publiée dans la brochure « Maths Nature express », éditée par le Comité International des Jeux Mathématiques à l’occasion du 9e salon « Culture et Jeux mathématiques ».
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Philippe de Reffye

Paul Henry Cournède