
Résoudre le Mini-Rubik’s Cube
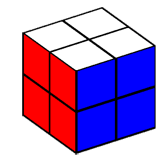
Petit frère du fameux Rubik’s Cube, le Mini-Rubik, encore appelé Pocket Cube, n’est composé que de huit petits cubes au lieu de 26. Si les configurations possibles du grand Rubik sont de 43 252 003 274 489 856 000, pour le Mini-Rubik elles ne sont que de 3 674 160, ce qui rend possible leur traitement exhaustif à l’aide d’un ordinateur. Cela permet donc d’écrire un petit programme qui résout le Mini-Rubik. Mais attention, traiter les configurations de façon exhaustive ne signifie pas chercher la solution au hasard !
Pour résoudre le cube, il s’agit, à partir de n’importe quelle configuration, de trouver un enchaînement de mouvements qui débouchera sur le cube reconstitué. Les mouvements à effectuer pour passer d’une configuration à une autre sont des rotations d’un ensemble de 4 petits cubes. Le programme que nous vous présentons ici trouvera toujours la solution qui nécessite le moins de mouvements.
Le modèle
Pour écrire ce programme, nous avons tout d’abord besoin de représenter le Mini-Rubik dans l’ordinateur, par un modèle. Celui que nous avons choisi est particulièrement adapté à cette tâche. D’autres modèles sont possibles, mais le nôtre permet en particulier d’expliquer pourquoi les configurations possibles du Mini-Rubik sont au nombre de 3 674 160.

Une première observation nous est utile pour définir le modèle : il est possible de résoudre le cube en conservant l’un de ses angles toujours dans la même position. Dans notre modèle, nous choisissons donc l’un des petits cubes, qui ne changera jamais de position et deviendra notre référentiel. Arbitrairement, nous décidons de placer celui de couleur bleu-blanc-rouge devant, en haut, sur la gauche.
Définir les mouvements
La deuxième étape est maintenant de caractériser les mouvements possibles. Ayant fixé le petit cube bleu-blanc-rouge, nous pouvons effectuer trois types de rotations.
La première possibilité est la rotation de la partie droite. Nous notons r (comme right) la rotation de la partie droite d’un quart de tour dans le sens des aiguilles d’une montre, r2 deux rotations successives d’un quart de tour (ou demi-tour). Enfin, trois rotations d’un quart de tour dans ce sens sont équivalentes à une rotation d’un quart de tour dans le sens inverse des aiguilles d’une montre, que nous notons r-1.
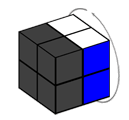
La deuxième possibilité est la rotation de la partie arrière. D’une façon similaire, nous notons les mouvements possibles b (comme back), b2 et b-1.
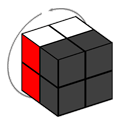
La dernière possibilité est la rotation de la partie basse, dont les mouvements sont notés d (comme down), d2 et d-1.
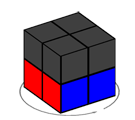
Nous n’avons pas à considérer les rotations des parties gauche, avant et haute, que l’on trouve dans d’autres modèles. En effet, ces rotations, qui modifieraient la position du cube bleu-blanc-rouge, sont équivalentes à celles que nous avons définies. Par exemple, une rotation d’un quart de tour de la partie gauche correspond à une rotation d’un quart de tour de la partie droite dans le sens inverse.
Pour vous familiariser avec ce modèle, nous vous proposons une première animation qui vous permettra de tester les 9 rotations.
En utilisant les boutons sur la gauche du cube, vous pouvez effectuer directement les rotations. En utilisant le mini-clavier, en dessous à gauche, vous pouvez programmer une séquence de rotations que vous pourrez ensuite exécuter grâce au bouton Lancer ou Pas à pas. Si vous parvenez à reconstituer le cube, le bouton Mélanger vous permettra de tester une autre configuration.
Représenter les configurations
Une fois définies les rotations utiles, il faut à présent trouver une méthode pour représenter chaque configuration de façon unique.
Pour représenter une configuration, nous utilisons les informations de position et d’orientation des 7 petits cubes que l’on peut déplacer. Arbitrairement, on numérote les différentes positions des cubes de 1 à 7 comme montré ci-dessous.

Initialement, on considère que le premier cube est en position 1, le deuxième cube en position 2, …, le septième cube en position 7. Ceci se représente par la séquence (1,2,3,4,5,6,7). Les positions des cubes d’une configuration sont toujours une permutation de cette séquence initiale. Par exemple, (2,4,6,1,3,5,7) indique que le deuxième cube est en première position, le quatrième cube en deuxième position, etc.
Une fois les petits cubes positionnés, il faut s’occuper de leur orientation. Chaque petit cube a seulement trois de ses six faces colorées. Il n’y a donc que trois orientations possibles. Si on considère le cube jaune-rouge-bleu, on peut avoir soit le jaune en haut, soit le rouge, soit le bleu.
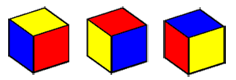

Pour représenter l’orientation des petits cubes, on numérote dans le sens des aiguilles d’une montre les faces colorées de chaque cube.
On choisit arbitrairement que c’est en regardant au-dessus du cube que l’on lit, directement ou par transparence, l’orientation des cubes. On décide, de plus, que dans la position initiale toutes les orientations sont à 1.
Pour l’orientation, on a donc la représentation de la position initiale montrée ci-dessous.

Une configuration est alors représentée par une séquence de 14 nombres (p1,p2,p3,p4,p5,p6,p7,o1,o2,o3,o4,o5,o6,o7) où pi représente le numéro du petit cube qui est en position i et oi son orientation. La représentation de la configuration initiale est (1,2,3,4,5,6,7,1,1,1,1,1,1,1).
Représenter les rotations
Une configuration ayant ainsi été définie, les rotations sont des objets qui font passer d’une configuration à une autre. En partant de la configuration (p1,p2,p3,p4,p5,p6,p7,o1,o2,o3,o4,o5,o6,o7) :
- la rotation r de la partie droite restitue la nouvelle configuration (p2,p5,p3,p1,p4,p6,p7,o2+,o5-,o3,o1-,o4+,o6,o7)
- la rotation b de la partie arrière restitue la nouvelle configuration (p1,p2,p3,p5,p6,p7,p4,o1,o2,o3,o5+,o6-,o7+,o4-)
- la rotation d de la partie basse restitue la nouvelle configuration (p1,p3,p6,p4,p2,p5,p7,o1,o3,o6,o4,o2,o5,o7)
o+ représente le pivotement d’un petit cube dans les sens des aiguilles d’une montre : on passe de l’orientation 1 à l’orientation 2, ou de l’orientation 2 à l’orientation 3, ou de l’orientation 3 à l’orientation 1.
o- représente le pivotement d’un petit cube dans les sens inverse des aiguilles d’une montre : on passe de l’orientation 1 à l’orientation 3, ou de l’orientation 2 à l’orientation 1, ou de l’orientation 3 à l’orientation 2.
Chaque rotation modifie les positions et les orientations de seulement 4 petits cubes. Par exemple, lorsqu’on effectue la rotation d’un quart de tour de la partie droite, le petit cube p2 qui se trouvait en position 2 se retrouve en position 1. Ceci se représente par le fait que p2 et o2 se retrouvent respectivement en première et huitième position dans la configuration. Dans cette rotation, le cube initialement en position 2 subit un pivotement dans le sens des aiguilles d’une montre, son orientation change donc positivement. Ceci explique la notation o2+.
Enfin, notre choix de lire les orientations en regardant au dessus du cube a pour conséquence que, dans la rotation de la partie basse, les valeurs des orientations ne sont pas modifiées.
Explorer le Mini-Rubik
Ayant ainsi modélisé le Mini-Rubik, on peut commencer à l’explorer à l’aide d’un ordinateur. Le premier programme pour résoudre le Mini-Rubik que l’on peut écrire est celui qui essaie aléatoirement des mouvements jusqu’à obtenir la position initiale, où il s’arrête. L’animation suivante vous permettra d’évaluer cette stratégie.
Pour essayer la stratégie aléatoire, cliquez sur le bouton Lancer. Si vous avez la chance de reconstituer le cube, le bouton Mélanger vous permettra d’essayer à nouveau à partir d’une autre configuration.
Pour résoudre le Mini-Rubik avec cette stratégie aléatoire, il faut être très chanceux ou extrêmement patient. En effet, le problème avec cette stratégie est que rien ne l’empêche de ré-explorer une configuration déjà rencontrée.
Pour écrire un programme capable de résoudre le cube le plus rapidement possible, il faut donc trouver une autre stratégie. Une idée est de calculer tout d’abord le nombre maximal de mouvements à effectuer entre une configuration quelconque et la solution. Si ce nombre n’est pas trop élevé, on peut envisager d’appliquer une stratégie de recherche itérative, aussi appelée recherche en largeur d’abord.
On montre qu’il est toujours possible de résoudre le Mini-Rubik en 11 mouvements ou moins. En effet, si on part du cube initial et que l’on considère toutes les configurations atteignables à partir de cette position initiale, on obtient neuf nouvelles configurations.
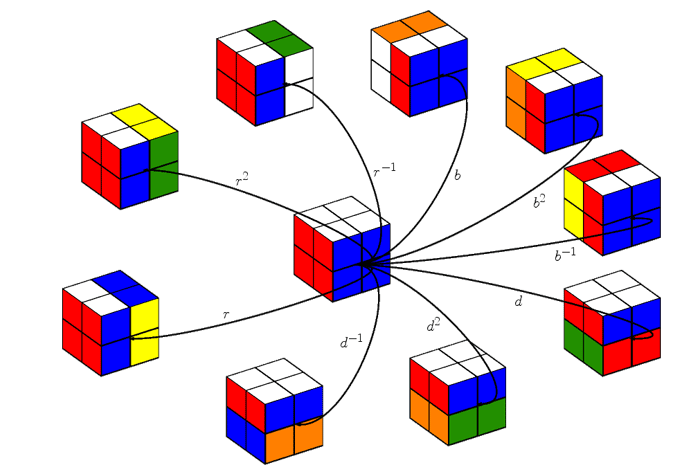
Si on recommence cette itération pour chacune de ces 9 nouvelles configurations, on obtient cette fois 54 nouvelles configurations. Continuant ce processus, on obtient respectivement 321, 1847, 9992, 50 136, 227 536, 870 072, 1 887 748, 623 800, 2644 et enfin 0 nouvelles configurations. Le fait que l’on ait besoin de 12 itérations pour qu’aucune nouvelle configuration ne soit générée prouve qu’on peut toujours résoudre le Mini-Rubik en 11 mouvements au plus.
Notons au passage que si on additionne toutes les nouvelles configurations obtenues par itérations successives, c’est-à-dire toutes les configurations atteignables, cela donne 1 + 9 + 54 + 321 + 1847 + 9992 + 50 136 + 227 536 + 870 072 + 1 887 748 + 623 800 + 2644 = 3 674 160. Il y a donc bien 3 674 160 configurations possibles du Mini-Rubik !
Stratégie de recherche itérative
Pour implémenter cette recherche itérative dans l’ordinateur, il faut pouvoir représenter efficacement des ensembles de configurations. Et surtout, il faut être capable de tester l’appartenance d’une configuration à un ensemble, et d’ajouter un élément à cet ensemble. Comme les ensembles que l’on doit manipuler peuvent avoir jusqu’à 3 millions d’éléments, il est important d’avoir une représentation compacte. Pour cela, la solution va s’articuler en deux étapes. Dans un premier temps, on explique comment associer à chaque configuration un nombre unique de 0 à 3 674 159. Ceci s’appelle l’indexation. Dans un deuxième temps, on montre comment, en utilisant les opérations sur les grands nombres, on se sert de ces grands ensembles pour résoudre le cube.
Indexer les configurations
Si on se rappelle notre représentation des configurations, une configuration est représentée par 14 nombres (p1,p2,p3,p4,p5,p6,p7,o1,o2,o3,o4,o5,o6,o7) où (p1,p2,p3,p4,p5,p6,p7) est une permutation de (1,2,3,4,5,6,7) et où les oi sont compris entre 1 et 3. Une première remarque est que si on regarde la configuration initiale et les différentes rotations, l’invariant (o1 + o2 + o3 + o4 + o5 + o6 + o7) mod 3 = 1 est préservé. En effet, il est vrai pour la configuration initiale, et dans la définition de chaque rotation, il y a autant de + que de -. Cet invariant indique que l’on peut en fait déduire la valeur de o7 des valeurs des autres orientations. Il y a donc un maximum de 7! permutations des pi et un maximum de 36 orientations, soit en tout un maximum de 7!36 = 3 674 160 configurations, on retrouve encore ce même nombre.
Pour trouver le numéro n d’indexation d’une configuration, on va indexer séparément la partie qui concerne les permutations, pour obtenir un nombre n1, et la partie qui concerne les orientations, pour obtenir un nombre n2. Comme il y a au maximum 36 orientations (donc 0 ≤ n2 < 36), on peut choisir n = n1 × 36 + n2.
Pour indexer les orientations, comme les oi sont compris entre 1 et 3, il suffit de prendre n2 = (o1 -1) + 3 × ((o2 – 1) + 3 × ((o3 – 1) + 3 × (( o4 – 1) + 3 × ((o5 – 1) + 3 × (o6 – 1))))).
Pour indexer les permutations, il existe différents algorithmes. Nous avons choisi un algorithme linéaire, dont le fonctionnement peut être expliqué de façon informelle sur un exemple. L’idée générale en est que l’on veut calculer la distance de la permutation que l’on indexe avec la permutation identité (1,2,3,4,5,6,7). Supposons que l’on veuille indexer la permutation (4,1,7,2,6,5,3).
- On s’intéresse tout d’abord au premier élément de la liste (ici 4) et on calcule la distance d1 à laquelle se trouve l’élément 1. Ici, il se trouve directement à sa droite, donc d1 = 1. On permute ensuite ces deux éléments 4 et 1 pour obtenir la nouvelle permutation (1,4,7,2,6,5,3), dont on est sûr que le premier élément est 1.
- On s’intéresse maintenant au deuxième élément de la liste (ici de nouveau 4) et on calcule la distance d2 à laquelle se trouve l’élément 2. On a d2 = 2 et on effectue une nouvelle permutation pour obtenir (1,2,7,4,6,5,3).
- Pour le troisième élément (7), on obtient d3 = 4, et (1,2,3,4,6,5,7).
- Pour le quatrième élément (4), on obtient d4 = 0, et (1,2,3,4,6,5,7).
- Pour le cinquième élément (6), on obtient d5 = 1, et (1,2,3,4,5,6,7).
- Enfin pour le sixième élement (6), on obtient d6 = 0, et la permutation identité (1,2,3,4,5,6,7).
Ces transformations sont toujours réversibles, et la distance di est toujours comprise entre 0 et 7 – i. Ainsi, on peut définir l’indexation n1 par la formule d6 + 2 × (d5 + 3 × (d4 + 4 × (d3 + 5 × (d2 + 6 × d1)))). Pour notre exemple, n1 = 1058. Avec cette indexation des permutations, l’index de la configuration initiale est n = 0.
Représenter les ensembles de configurations
Une fois les configurations indexées, on peut utiliser les grands nombres pour représenter les ensembles de configurations. Pour représenter chaque ensemble de configurations dont on a besoin, on utilise un nombre dont le codage binaire comprend 3 674 160 bits. Chacun de ses bits représente une configuration, il est à 1 si la configuration appartient à l’ensemble considéré, et à 0 si elle n’en fait pas partie.
0 représente ainsi l’ensemble vide {}. Si le nombre NS représente l’ensemble S, pour tester si une configuration c est dans S, il faut calculer n l’index de c et tester que (NS/2n) mod 2 est égal à 1, ce qui revient à tester le n-ième bit de NS. Si c n’est pas dans S, le fait d’ajouter c à S est représenté par le nombre NS + 2n, c’est-à-dire qu’on met le n-ième bit de NS à 1.
Cette représentation des ensembles se sert du fait que l’arithmétique sous-jacente des ordinateurs est binaire : diviser et multiplier par une puissance de 2 sont des opérations très efficaces.
Résoudre le Mini-Rubik
Écrire un programme qui résout le Mini-Rubik est maintenant simple. Comme on sait indexer n’importe quelle configuration, il suffit d’associer, dans une table, à chaque configuration le nombre de mouvements N nécessaires pour la résoudre. La construction de cette table se fait simplement par un processus d’exploration itérative partant de la position initiale. Cette table a 3 674 160 entrées.
Une fois une telle table construite, pour résoudre une configuration donnée, il faut dans un premier temps lire dans la table le nombre N de mouvements nécessaires pour la résoudre. Ensuite, on applique chacune des 9 rotations pour trouver les 9 configurations voisines, dont on calcule l’index. On lit alors dans la table le nombre de mouvements nécessaires pour résoudre ces voisins.
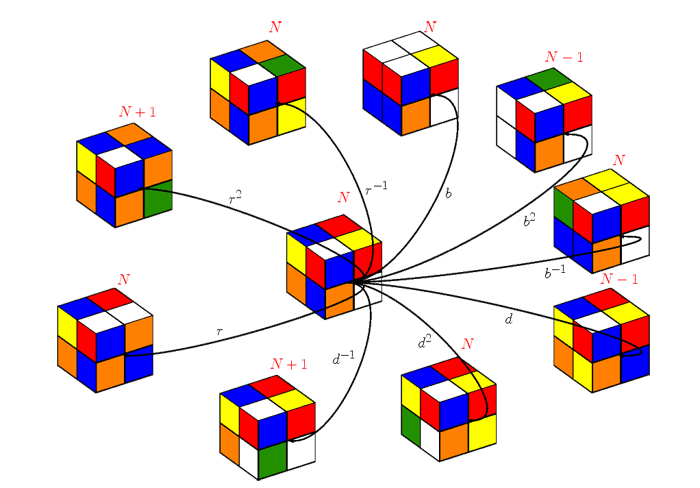
Il suffit alors de choisir un voisin ayant pour valeur associée N-1. En répétant le processus sur ce voisin, on se rapproche pas-à-pas de la configuration initiale.
Mais en fait, on peut encore simplifier les choses. On note en effet que si une configuration peut être résolue en N mouvements, alors ses voisins peuvent être résolus en N-1, N ou N + 1 mouvements. Or tout ce dont on a besoin, c’est d’être capable de sélectionner un voisin dont la valeur associée est N-1. Dans la table, il est donc suffisant d’associer à chaque configuration non pas le nombre N, mais N modulo 3, car quelle que soit la valeur de N, (N-1) mod 3, N mod 3 ou (N + 1) mod 3 sont toujours trois valeurs distinctes, 0, 1 ou 2. Pour construire une table qui associe ainsi à chaque configuration sa distance à la configuration initiale modulo 3, c’est-à-dire une information qui tient sur 2 bits, comme on a 3 674 160 configurations, on n’a donc besoin que d’un peu plus de 7 millions de bits, soit un peu moins de 1 Méga-octet.
Le programme en action
Voici finalement une petite application graphique qui permet de résoudre le Mini-Rubik.
Le programme présente une solution que vous pouvez explorer avec les boutons Lancer ou Pas à pas. Une fois le cube reconstitué, pour partir d’une autre configuration, vous pouvez utiliser le bouton Mélanger ou la modifier manuellement avec les boutons de rotation à gauche.
Conclusion
Ce document explique comment construire un programme qui résout le Mini-Rubik. La clé de cette construction est la capacité d’indexer les configurations possibles du Mini-Rubik. Ceci nous permet de construire une table d’un Méga-octet qui est utilisée pour la résolution.
La correction d’un tel programme est loin d’être évidente. Pour s’en convaincre, on peut, par exemple, essayer de vérifier que partant de la position initiale, le programme trouve bien à chaque nouvelle itération respectivement 9, 54, 321, 1847, 9992, 50 136, 227 536, 870 072, 1 887 748, 623 800, et enfin 2644 nouvelles configurations. Mais ce n’est clairement pas suffisant. Afin d’obtenir une réelle assurance de la correction du programme, il faut en faire la preuve formelle en utilisant un outil d’aide à la preuve. Ceci est possible, et a été réalisé dans l’outil de preuve Coq.
Réalisation des animations : Ouest INSA, sur la base des applets réalisées à partir du programme par Hamdi Ben Abdallah.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
