
Le jeu de go et la révolution de Monte Carlo
Depuis les débuts de l’informatique, les chercheurs tentent de construire des machines capables de rivaliser avec le cerveau humain. Les jeux sont pour eux un terrain d’expérimentation privilégié. En 1997, Deep Blue, un super-ordinateur construit par IBM, a battu aux échecs le champion du monde, Garry Kasparov. Ce succès a eu un retentissement important, mais les ordinateurs ne sont pas devenus plus intelligents que les humains pour autant. Il reste de nombreux domaines où le cerveau humain surpasse largement les capacités des ordinateurs les plus puissants.
Un de ces domaines où les ordinateurs ne sont pas à la hauteur du cerveau humain est le jeu de go. Né il y a plusieurs milliers d’années en Chine, ce jeu est très populaire en Extrême Orient (Japon, Chine et Corée, essentiellement). Pendant très longtemps, les meilleurs programmes de go sont restés au niveau des joueurs humains faibles. Quelques semaines de pratique suffisaient à un débutant motivé pour parvenir à battre les meilleurs programmes joueurs de go.
Même si les programmes de go actuels restent beaucoup plus faibles que les meilleurs humains, une révolution technologique a récemment permis aux ordinateurs de faire un grand pas en avant. Les programmes de go ont fait des progrès spectaculaires grâce aux méthodes dites « de Monte Carlo ». Ces méthodes consistent à ne considérer qu’un petit nombre de séquences de coups, choisies aléatoirement parmi l’immensité de toutes les séquences possibles. Quels sont les principes de ces algorithmes, et comment s’appliquent-ils au go ?
Problèmes de complexité dans les jeux à deux joueurs
Principe de la recherche arborescente
La recherche arborescente est à la base de la plupart des algorithmes utilisés pour les programmes de jeux à deux joueurs. Leur principe de fonctionnement peut s’illustrer simplement avec le jeu du morpion ou tic-tac-toe. Au morpion, chaque joueur à son tour dessine un rond ou une croix sur une grille 3×3. Le but est d’aligner trois mêmes symboles horizontalement, verticalement, ou en diagonale. Par exemple, dans la position suivante, c’est au joueur dessinant les croix de jouer :
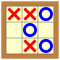
En réfléchissant un peu, on se rend compte rapidement que, où que joue le joueur dessinant les croix, celui qui dessine les ronds peut gagner au coup suivant, soit en jouant dans le coin inférieur gauche, soit en jouant au milieu à droite. Donc cette position est perdue pour l’autre joueur.
Pour recréer artificiellement ce genre de raisonnement, les ordinateurs peuvent utiliser une recherche arborescente. Il s’agit d’observer toutes les séquences possibles. Par exemple, l’arbre de recherche de cette position est le suivant :
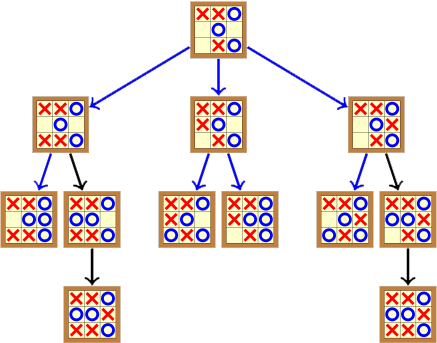
Dans ce dessin, les flèches bleues pointent vers une position gagnée par le joueur qui dessine les ronds, et les flèches noires pointent vers une position nulle (aucun gagnant). La valeur des positions terminales est déterminée par les règles du jeu. La valeur des positions non-terminales (à l’intérieur de l’arbre) peut se calculer en fonction de la valeur des positions qui sont en dessous d’elles. On peut ainsi remonter jusqu’à la position initiale (la « racine » de l’arbre), et déterminer que c’est une position gagnante pour le joueur dessinant les ronds, vu que toutes les flèches qui en partent sont bleues.
En fait, il n’est pas nécessaire d’explorer l’intégralité de cet arbre pour déterminer la valeur théorique de la position racine. En effet, dès qu’on a trouvé un coup gagnant pour les ronds dans une position où c’est au joueur qui les dessine de jouer, il n’est pas nécessaire d’analyser les autres coups. Pour gagner, il suffit d’avoir un seul coup gagnant, peu importe la valeur des autres coups. On se retrouve ainsi avec l’arbre minimal suivant :
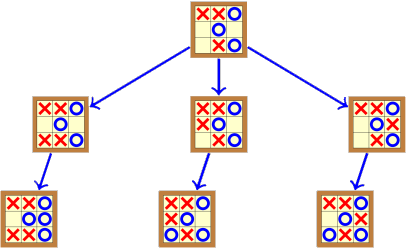
Complexité des jeux
La recherche arborescente est une méthode très simple et efficace pour le morpion, mais elle se heurte à de grosses difficultés pour des jeux plus complexes. Imaginons par exemple que l’on joue au morpion sur une grille 10×10 au lieu de 3×3, avec l’objectif d’aligner 6 pions au lieu de 3. Disons que l’on cherche à analyser toutes les séquences possibles de longueur 10 à partir du plateau vide (ce qui est largement insuffisant pour déterminer le coup optimal). On se retrouve alors face à un nombre de possibilités égal à 100 × 99 × 98 × 97 × 96 × 95 × 94 × 93 × 92 × 91 = 62.815.650.955.529.472.000. Ce nombre est trop élevé pour être énuméré même par les ordinateurs les plus puissants.
Il est possible d’utiliser un certain nombre d’astuces qui permettent de réduire la complexité. Comme on l’a vu précédemment, il n’est pas nécessaire de pousser l’analyse d’une position plus loin à partir du moment où on a trouvé un coup gagnant : les autres coups ne peuvent pas être meilleurs. D’autre part, on peut aussi réduire la complexité en utilisant les propriétés spécifiques du problème. Au morpion, par exemple, la valeur d’une position est invariante par symétrie ou rotation. En utilisant ce genre d’idées, on peut réduire la complexité du problème de plusieurs ordres de grandeur.
Malgré ces astuces qui permettent de réduire la complexité, de nombreux jeux sont complètement hors de portée d’une résolution formelle par une recherche arborescente. Le tableau suivant résume la situation de quelques jeux importants :
| Jeu | Complexité | État de l’art |
|---|---|---|
| Morpion | 103 | Résolu (à la main) : partie nulle si les joueurs jouent bien |
| Puissance 4 | 1014 | Résolu en 1988 : le joueur qui commence a une stratégie gagnante |
| Dames anglaises | 1020 | Résolu en 2007 : partie nulle si les joueurs jouent bien |
| Échecs | 1050 | Non résolu. Les programmes sont meilleurs que les meilleurs humains |
| Go | 10171 | Non résolu. Les programmes sont bien plus faibles que les meilleurs humains |
La complexité indiquée dans ce tableau correspond au nombre approximatif de configurations possibles du plateau de jeu. Un jeu est considéré comme résolu à partir du moment où on a une preuve formelle sur la stratégie optimale. Même si les programmes joueurs d’échecs sont beaucoup plus forts que les meilleurs humains, le jeu est encore très loin d’être résolu formellement.
Le jeu de go
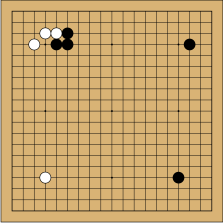
Une configuration de début de partie de go.
Parmi les jeux de plateau classiques, le jeu de go s’avère donc nettement plus complexe que les autres. Et les meilleurs programmes sont encore faibles par rapport aux meilleurs humains. Le jeu de go se joue sur une grille de 19×19 lignes. Deux joueurs posent alternativement des pierres blanches et noires sur les intersections de cette grille. Le but du jeu est de contrôler avec ces pierres la plus grande surface possible du plateau. Les lecteurs qui ne connaissent pas le jeu et souhaitent s’initier trouveront toutes les informations nécessaires sur le site Jeu de go.
Même sans comprendre le détail des règles, on peut se rendre compte du problème de complexité : 361 coups possibles au début, contre 20 aux échecs. Il est énormément plus coûteux de développer un arbre de recherche profond au go qu’aux échecs.
Comment gérer la complexité ?
Quand les méthodes exactes ne permettent pas de déterminer de manière formelle la stratégie optimale, il est nécessaire d’utiliser des méthodes approchées.
L’approche classique : limiter la profondeur de l’arbre
Utilisée dans les programmes d’échecs ou de dames, l’approche classique consiste à limiter la profondeur de l’arbre. Il s’agit d’étudier les positions après un petit nombre de coups fixé, ce qui permet de réduire la combinatoire. En réduisant ainsi la profondeur de l’arbre, les feuilles ne correspondent plus à la fin d’une partie. On ne peut alors généralement pas en déterminer de manière formelle le gagnant. On remplace alors la valeur formelle de ces positions par ce qu’on appelle une évaluation heuristique. Cette évaluation est représentée par un E dans la figure suivante :
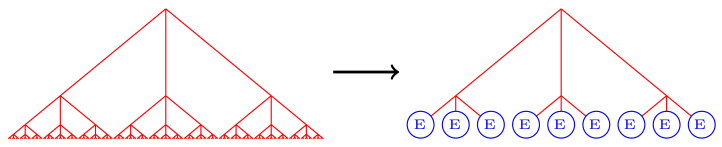
Par exemple, aux échecs, cette heuristique se base souvent sur le comptage du matériel : 9 points pour une dame, 5 points pour une tour, 3 points pour un fou ou un cavalier, 1 point pour un pion. À cette évaluation matérielle s’ajoutent des termes liés à la position des pièces, comme la mobilité ou la sécurité du roi. On peut ainsi obtenir une estimation approximative de la position en analysant la différence de force entre les deux armées.
L’approche de Monte Carlo
L’approche classique a donné de très bon résultats pour les échecs, mais a échoué pour le go. Les programmes de go basés sur une recherche arborescente de profondeur limitée sont tous très faibles. Pourquoi ? Une des difficultés essentielles du go est la définition d’une bonne fonction d’évaluation heuristique. Alors qu’aux échecs il est simple et efficace de mesurer la force des deux armées en présence en comptant le nombre de pièces, il est très difficile d’estimer les territoires dans une position de go.
Afin de contourner cette difficulté dans la construction de fonctions d’évaluation heuristiques, l’approche de Monte Carlo consiste à systématiquement explorer les branches de l’arbre jusqu’à une position terminale. Étant donné le nombre astronomiquement élevé de parties possibles, cette approche ne peut pas explorer exhaustivement toutes les possibilités : il faut donc choisir un sous-ensemble des parties possibles. C’est ce qui est schématisé dans la figure suivante :
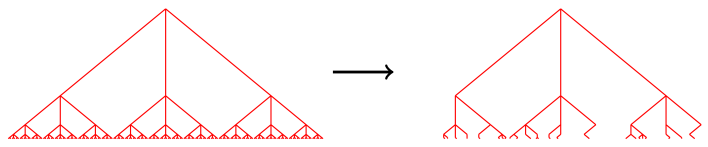
En se basant sur ce principe d’exploration partielle de l’arbre jusqu’aux feuilles, la mise au point d’un algorithme Monte Carlo efficace repose sur deux problèmes essentiels. Le premier est le choix des séquences à explorer : comment choisir celles qu’on explore parmi toutes les possibilités ? Le second problème est celui de l’évaluation des coups : étant données les séquences observées et leur résultat (gagné ou perdu, dans le cas du go), comment déterminer le meilleur coup ? Une grande variété d’algorithmes a été proposée ces dernières années pour répondre à ces deux questions. C’est encore un domaine de recherche très actif, où il reste certainement des idées importantes à découvrir.
Un des algorithmes les plus primitifs consiste à simplement choisir les coups aléatoirement, et à évaluer chaque position par la moyenne du résultat de toutes les parties aléatoires qui passent par cette position. Ce principe est schématisé dans la figure suivante :
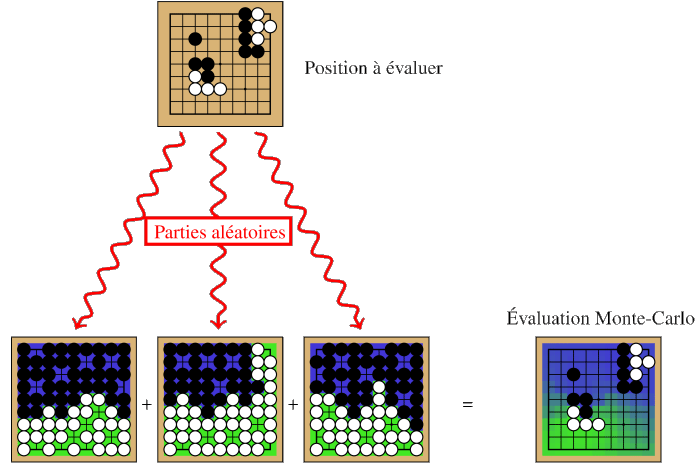
Pour chacun des coups possibles, la moyenne des résultats des parties obtenues après avoir joué ce coup donne une estimation de sa valeur. Il suffit ensuite de choisir le coup qui mène vers la position qui a la meilleure moyenne. Pour donner un ordre de grandeur, les meilleurs programmes actuels parviennent à générer plusieurs dizaines de milliers de parties aléatoires par seconde sur un PC puissant.
À partir de cette idée primitive, de nombreuses améliorations ont été apportées à l’algorithme. Sans entrer dans les détails, les idées essentielles sont les suivantes :
- Ne pas choisir les coups de manière uniformément aléatoire. Certains coups qui semblent meilleurs a priori (comme répondre à une menace immédiate) peuvent être choisis avec une probabilité plus élevée, ce qui améliore la précision de l’évaluation.
- Augmenter la probabilité de choisir un coup qui s’est avéré être bon dans les simulations précédentes.
La plupart des programmes de go actuels se basent sur ces deux idées.
Historique de la recherche arborescente Monte Carlo
Les pionniers
En 1993, Bernd Brügmann, physicien, écrit le premier programme de go utilisant une méthode de Monte Carlo. À l’époque, personne n’a vraiment pris cette idée au sérieux. Bernd Brügmann lui-même la considérait comme un peu farfelue.
Elle passe donc aux oubliettes jusqu’à ce qu’en 2000, les chercheurs parisiens Bruno Bouzy, Tristan Cazenave et Bernard Helmstetter remettent l’idée de Bernd Brügmann au goût du jour. Leurs travaux ne leur permettent pas encore de surpasser les programmes classiques, mais ils font des progrès.
Succès contre les programmes classiques
En 2006, le programme Crazy Stone que j’ai développé gagne la médaille d’or de la Computer Olympiad en 9×9. Il s’agit d’un tournoi annuel où les programmeurs du monde entier se rencontrent et jouent des compétitions. Cette médaille d’or était la première victoire d’un programme Monte Carlo dans un tournoi important. À partir de ce moment, de nombreux programmeurs se mettent aux méthodes de Monte Carlo.
En 2007, MoGo, un nouveau programme français développé depuis 2006, gagne la médaille d’or de la Computer Olympiad en 19×19. Cette victoire marque le début de la domination complète des programmes Monte Carlo sur les programmes classiques.
Quelles différences entre Crazy Stone et MoGo ? En fait, les principes essentiels de fonctionnement de ces deux programmes sont quasiment identiques. Nous nous sommes inspirés les uns des autres au cours du développement. Il y a des différences, bien sûr, mais au niveau de détails techniques dans lesquels nous n’entrerons pas ici.
Succès contre les joueurs professionnels

Kaori Aoba commente sa partie après sa défaite contre Crazy Stone lors de la deuxième édition de l’UEC Cup, en décembre 2008, à Tokyo. Crazy Stone avait les noirs, et jouait avec 7 pierres de handicap.
Après avoir dépassé les programmes classiques, les programmes Monte Carlo ont poursuivi leur progression fulgurante. Qu’il s’agisse de Crazy Stone ou de MoGo, leurs victoires contre des joueurs professionnels montrent cette progression.
- mars 2008 : MoGo bat Catalin Taranu (pro. 5 dans) sur le petit plateau (9×9).
- août 2008 : MoGo bat Kim Myungwan (pro. 9 dans) à 9 pierres de handicap.
- septembre 2008 : Crazy Stone bat Kaori Aoba (pro. 4 dans) à 8 pierres de handicap.
- décembre 2008 : Crazy Stone bat Kaori Aoba (pro. 4 dans) à 7 pierres de handicap.
- février 2009 : MoGo bat Li-Chen Chien (pro 1 dan) à 6 pierres de handicap.
Où s’arrêteront-ils ?
Le développement des méthodes de Monte Carlo pour la recherche arborescente a permis aux programmes joueurs de go de faire des progrès fulgurants ces dernières années. Mais les meilleurs programmes actuels sont encore très loin du niveau des meilleurs professionnels. Ce domaine de recherche reste très ouvert, et on peut imaginer que les programmes vont continuer à progresser à un rythme régulier pendant encore de nombreuses années. Il est probable qu’on arrivera un jour à des programmes plus forts que les meilleurs joueurs humains, mais il est difficile de dire si cela va prendre 10 ou 100 ans…
Mise à jour de mai 2014 : 5 ans après l’écriture de cet article, les ordinateurs n’ont pas encore atteint le niveau des meilleurs humains, mais ils progressent. Crazy Stone vient de battre Norimoto Yoda (professionnel 9 dan) avec 4 pierres de handicap lors de la deuxième édition du densei-sen à Tokyo, au Japon. Les programmes se rapprochent des champions humains, mais les progrès sont de plus en plus lents et difficiles. Il faudra encore développer des innovations majeures pour atteindre le plus haut niveau.
- Le jeu de go, tout ce qu’il faut savoir pour jouer : les règles, les clubs, les sites Web.
- MoGo, maître du jeu de Go ? : document Interstices de 2006 sur un sujet similaire.
- L’historique de Crazy Stone.
- Testez Leela, une version de démonstration gratuite pour Windows, qui fonctionne avec les mêmes algorithmes que Crazy Stone.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Rémi Coulom