
Calculer différemment
Dans les années 1930, plusieurs notions de calcul sont inventées afin de capturer de manière abstraite l’idée de manipuler mécaniquement des séries de symboles pris dans un ensemble fini. Elles se révèlent toutes équivalentes par traduction d’un formalisme dans un autre. Mieux, il existe une machine universelle abstraite qui peut simuler le fonctionnement de tout calcul. Cette machine universelle représente le calcul à effectuer par un programme, ce programme étant stocké dans la mémoire de la machine, tout comme les données sur lesquelles s’effectue le calcul. Ce calculateur universel abstrait peut se construire physiquement, et depuis les années 1950, les performances des ordinateurs, qui concrétisent cette implantation, doublent à peu près tous les deux ans.
Est-ce à dire que nous sommes arrivés à la fin de cette belle histoire ? Bien sûr, nous sommes loin d’avoir fait le tour de la notion de programme, nous continuons notre quête d’ordinateurs plus rapides et il y a peu de risques de se tromper en prédisant que de nouvelles utilisations utiles et surprenantes de nos systèmes informatiques restent encore à inventer. Mais avons-nous fait le tour de la notion de calcul ? Tout se ramène-t-il toujours au calculateur universel ? Les frontières du continent qu’Alan Turing a ouvert pour nous sont-elles définitivement figées ?
La réponse est non, et les terrae incognitae qui restent à explorer promettent encore de beaux voyages pour longtemps. Les chercheurs essayent de dépasser les limitations des machines de Turing pour calculer plus, pour calculer autrement, pour calculer plus vite ou pour calculer mieux.
Au-delà du calculable : calculer plus
Peut-on proposer une procédure effective, que tout le monde reconnaîtra comme bien déterminée et sans ambiguïté, et qui permette de résoudre un problème insolvable par une machine de Turing ? Un tel dispositif généraliserait la notion de calcul.
La difficulté porte sur l’adjectif « effectif ». Quand elle a été conçue, la machine de Turing était une machine abstraite qui capturait la notion d’algorithme que pouvait dérouler un opérateur humain avec un crayon et un papier en un temps fini. Cette machine abstraite s’est ensuite concrétisée dans un système physique, une machine concrète obéissant aux lois de la physique. Nos ordinateurs utilisent les phénomènes électriques pour réaliser (une variante de) la machine de Turing, mais on peut aussi utiliser la mécanique newtonienne, comme le montre un prototype réalisé en LEGO.
Calcul et lois physiques
On peut donc essayer d’attaquer le problème en qualifiant d’effectif ce qui « peut se réaliser par un dispositif matériel ». Cette approche ouvre de nouvelles questions passionnantes en physique. Richard Feynman, prix Nobel de physique, est l’un des premiers à s’être intéressé à ces questions. Savoir ce qui peut être calculé par un système physique est un problème qui n’a pas reçu de réponse définitive et qui est largement ouvert.
À titre d’exemple, voici comment on peut calculer le plus petit commun multiple (PPCM) de deux nombres p et q avec un billard. Ce problème est facile à programmer sur nos ordinateurs, mais cet exemple montre qu’on peut « utiliser directement » un phénomène physique, ici la mécanique newtonienne, pour réaliser un algorithme.

Calculer le PPCM de 4 et 6 avec une table de billard.

Robin Gandy. Source : Alan Turing Scrapbook.
À la fin des années 1970, Robin Gandy, qui fut le seul étudiant en thèse encadré par Alan Turing, montre que tout dispositif physique qui respecte quatre principes relativement généraux ne pourra pas calculer autre chose que ce que peut calculer une machine de Turing. Les principes qui contraignent le dispositif sont les suivants :
- le dispositif est caractérisé par une suite discrète d’états ;
- chaque état est un assemblage d’un nombre fini de parties élémentaires non nécessairement disjointes mais qui ne peuvent être infiniment variées (il n’y a qu’un nombre fixé a priori de types de parties, mais le nombre de ces parties peut croître au cours du temps) ;
- le passage d’un état à un autre est déterministe ;
- et il n’y a pas d’actions instantanées à distance.
Ces contraintes traduisent des contraintes physiques : les éléments de la machine ont une taille minimale, la machine a une taille fixée à chaque instant (même si elle peut s’étendre), les transitions de la machine sont bien définies et il y a une vitesse maximale à la propagation de l’information (matière, énergie).
Gandy fait l’hypothèse que le dispositif physique est caractérisé par une suite discrète d’états et que ces états peuvent se décrire à chaque instant par un processus fini. C’est une contrainte importante que nombre de systèmes physiques ne vérifient pas. En effet, la description correcte d’un système physique implique souvent des quantités continues (le temps, la position, etc.). Et une quantité continue implique de manipuler une infinité d’informations. Par exemple, pour décrire un nombre réel, je dois donner toutes ses décimales et il y en a un nombre infini.
Certains nombres réels peuvent se décrire de manière finie : par exemple on peut « compresser » la constante π = 3,1415926535… en la représentant par un programme qui, pour un nombre entier n donné, retourne la n-ième décimale de π. Mais la plupart des nombres réels ne sont pas représentables de cette manière et ne peuvent donc pas être manipulés par une machine de Turing. Pour s’en rendre compte, on utilise un argument de comptage. On peut voir un programme comme un mot écrit avec certains symboles. Il est donc possible de classer tous les programmes comme dans le dictionnaire, en suivant l’ordre lexicographique, ce qui permet de les numéroter avec un entier. Cet argument montre qu’il y a autant de programmes que d’entiers, pas plus. Or le mathématicien Georg Cantor a montré qu’il y a bien plus de nombre réels que d’entiers.
Cela ouvre la possibilité d’utiliser un phénomène physique permettant de calculer une fonction qui ne serait pas calculable par une machine de Turing, par exemple de la manière suivante :
- on entre les données du calcul à effectuer, ce qui détermine les conditions initiales du système physique ;
- on laisse le système évoluer continûment pendant un temps fini ;
- et on récupère les résultats du calcul en mesurant un comportement observable du système.
Pour mettre en œuvre un tel dispositif, il faut préciser ce qu’il est possible de déterminer comme conditions initiales, comme évolution continue, et ce qu’il est possible de mesurer. Ces trois questions font l’objet d’intenses débats. Par exemple, la détermination des conditions initiales doit elle-même être calculable et ne doit pas requérir une quantité infinie d’informations, ou encore, on ne peut pas faire une mesure avec une précision infinie.
À ce jour, même s’il existe de nombreuses propositions, personne n’a construit un tel dispositif. Mais l’impossibilité d’en construire un n’a pas été établie formellement.
Une machine à calculer avec des trous noirs
Nous ne donnerons qu’un seul exemple, qui repose sur la physique relativiste et qui donnera une idée des débats. Cet exemple est l’un des plus convaincants, parce que les conditions initiales et la mesure n’amènent pas trop de questions et que, d’une certaine manière, il repose quand même sur une machine de Turing.
Supposons que l’on veuille établir s’il existe un nombre entier n vérifiant une certaine propriété P. Cette propriété doit être facile à établir pour un entier n donné ; la difficulté est de trouver un n qui la vérifie ou bien de montrer qu’il n’en n’existe pas. Par exemple P(n) est vraie si n est un nombre pair supérieur à 2 et qui ne peut pas s’écrire comme la somme de deux nombres premiers. Trouver un n satisfaisant cette propriété P ou établir qu’il n’existe pas résoudrait l’un des plus vieux problèmes de la théorie des nombres : la conjecture de Goldbach.
Une manière « simple » de résoudre ce problème est d’énumérer successivement les entiers n et de regarder si P est vraie ou pas pour chacun d’eux. Si un n vérifiant P existe, on peut fournir la réponse en temps fini. Mais si un tel n n’existe pas, il faut attendre infiniment (d’avoir examiné tous les entiers) avant de pouvoir répondre. Ce n’est donc pas un calcul (un algorithme) au sens de Turing.
Pour transformer cette procédure en un calcul, il suffirait donc de « compresser » une quantité infinie d’opérations, l’examen de chacun des n, en un temps fini. Une machine capable de cette prouesse est appelée une machine de Zénon, en référence aux paradoxes de Zénon d’Élée.
Philosophe grec, Zénon d’Élée (né vers −480 et mort vers −420) réfutait l’existence du mouvement, par exemple en invoquant qu’un mobile doit passer par une infinité de points avant d’arriver à destination, et qu’il ne peut donc y arriver en un temps fini. Une flèche qui va vers sa cible, ou Achille qui rejoint la Tortue, sont donc des exemples de machines de Zénon.
Or la physique relativiste offre un moyen de créer un calculateur de Zénon capable d’effectuer une infinité d’opérations en un temps fini.
Pour cela, il faut un trou noir d’un type assez particulier, mais dont l’existence est plausible, qui permet à un observateur de suivre une trajectoire géodésique pour franchir l’horizon du trou noir sans être écrasé par les forces gravitationnelles. Pour un observateur à l’intérieur du satellite, le temps à l’extérieur semble se comprimer de telle manière que tout événement dans le reste de l’univers apparaît se produire dans le référentiel du satellite avant le franchissement de l’horizon du trou noir. Le franchissement se fait à un temps T que l’observateur peut déterminer sans problème.
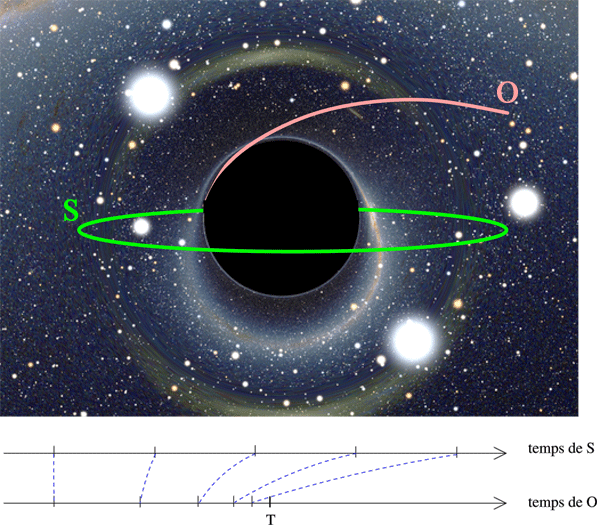
Calculer au-delà de Turing avec un trou noir.
Le principe du calcul est donc le suivant : un satellite S embarque un ordinateur classique chargé d’appliquer la procédure précédente pour trouver un n. Ce satellite orbite indéfiniment autour du trou noir. S’il trouve un n, il signale par radio le n trouvé à un observateur O qui chute vers le trou noir (voir figure ci-dessus). Si l’observateur ne reçoit aucun signal jusqu’au temps T (dans son repère local), il sait de manière certaine que l’énumération de tous les n a été effectuée et donc qu’aucun n ne vérifie P.
Il n’est pas établi que ce calculateur est réalisable physiquement, et voici quelques objections qui n’épuisent pas les questions qui se posent :
- l’existence de trous noirs du bon type n’est encore que postulée ;
- le satellite doit émettre un signal qui sera déformé par la gravitation du trou noir (mais cette déformation pourrait être compensée) ;
- le signal reçu doit être reconnu par l’observateur comme celui émis par le satellite et non par un autre événement (mais l’usage d’un codage approprié devrait pouvoir résoudre ce problème) ;
- l’observateur O doit être sur une trajectoire lui permettant de repartir avec l’information (ce qui n’est pas évident, car il faut échapper au trou noir) ;
- il faut que le calculateur ne tombe pas en panne pendant une durée de temps arbitrairement longue (potentiellement éternellement) ;
- si l’on prend en compte les effets quantiques, le trou noir « s’évapore », certes très lentement, mais cela borne le temps disponible pour le calculateur dans le satellite. Les effets quantiques doivent aussi jouer quand le satellite est très près de l’horizon (de l’ordre de la longueur de Planck) et il n’est pas dit qu’à cette échelle, la description donnée par la physique relativiste soit toujours correcte ;
- il faut aussi que le satellite dispose d’une source d’énergie lui permettant d’effectuer un calcul qui dure potentiellement un temps infini. Ce dernier point semble rédhibitoire, mais Richard Feynman a montré que, théoriquement, il était possible de faire des calculs sans consommer d’énergie. Il faut en particulier que chaque opération du calculateur soit réversible. Edward Fredkin et Tommaso Toffoli ont proposé un modèle théorique de machine de Turing réversible.
Le dispositif que nous venons de décrire semble donc bien loin d’être réalisable. Mais est-il plus irréaliste à nos yeux que ne pouvaient l’être nos ordinateurs aux yeux d’un chercheur d’il y a un siècle ? En tout cas, ces expériences, même si elles restent de pensée, permettent de pousser à bout les conséquences de nos théories du calcul et de la physique, et par là, sont pleines d’enseignement à la fois pour l’informatique et pour la physique.
L’espoir d’autres complexités : calculer autrement
Si les travaux sur les modèles de calcul permettant d’aller au-delà de ce qui est calculable par une machine de Turing semblent encore très spéculatifs, la recherche de modèles de calcul permettant de calculer plus vite (mais la même chose) qu’une machine de Turing est par contre un domaine dont les résultats semblent plus atteignables à court terme.
La complexité des algorithmes se mesure par deux fonctions qui indiquent le nombre d’opérations élémentaires (complexité en temps) et l’espace mémoire (complexité en espace) nécessaires pour accomplir un calcul sur une donnée d’entrée de taille n. On exprime ces fonctions pour le pire cas ou bien en moyenne. Par exemple, quand on dit qu’il existe un algorithme de tri en temps O(n2), cela veut dire que le nombre d’opérations nécessaires pour trier une liste de n nombres est de l’ordre du carré de la longueur de la liste. La notation O(…) indique qu’on donne la fonction à une constante multiplicative près (indépendante de n).
La complexité en temps et en espace permet d’affiner la notion de calculabilité. Au lieu de regarder si une fonction est calculable ou pas, on se pose la question (dans le cas où elle est calculable) de savoir si on peut la calculer efficacement ou pas. Les algorithmes dont la complexité est linéaire ou bien polynomiale peuvent traiter de grandes quantités de données. Par contre, si la complexité est exponentielle, nos ordinateurs doivent déclarer forfait dès que n augmente un peu. Supposons par exemple un algorithme de complexité en temps de O(2n) qui utilise 0.001 seconde pour s’exécuter sur une donnée en entrée de taille n = 10 sur notre ordinateur le plus rapide. Pour n = 60, ce qui n’est pas beaucoup plus grand, il faudra alors 366 siècles pour exécuter le même algorithme sur notre ordinateur le plus rapide. L’algorithme, même s’il existe, est inutilisable en pratique.
La complexité d’un algorithme est dépendante de la machine utilisée pour exécuter le calcul. Et donc, même si de nouveaux modèles de calcul ne permettent pas de dépasser la machine de Turing, il est possible qu’ils offrent de meilleures complexités.
Donnons un exemple. La recherche du maximum d’un ensemble de n nombres prend un temps O(n) sur un de nos ordinateurs, car il faut parcourir tous les nombres pour garder le plus grand. Il est possible d’imaginer un dispositif physique qui permette de trouver ce nombre en une seule opération, donc en O(1) : c’est la machine à spaghettis, décrite par A. K. Dewdney dans la revue Scientific American en juin 1984 : « On the Spaghetti Computer and other Analog Gadgets for Problem Solving ». Vous pouvez réaliser vous-même sans difficulté une machine à spaghettis. Cette machine n’offre en effet qu’une seule opération consistant à relâcher un fagot de spaghettis (non cuits !) tenu verticalement sur une table, tout en les maintenant par une légère pression de la paume de la main par le dessus. L’idée est de représenter chaque nombre q par un spaghetti de longueur q. Quand on relâche les spaghettis, les plus petits retombent car ils ne sont pas maintenus par la paume de la main, qui ne retient que le spaghetti le plus grand. Et voilà.
Est-ce que cela fonctionne ? Jugez-en sur la vidéo ci-dessous, et tentez l’expérience !
Visionner la vidéo – Durée : 34 s.
L’exemple précédent n’est pas très attractif, car il ne permet de gagner qu’un facteur n. Et personne n’envisage réellement de construire une machine à retenir les spaghettis…
Mais voici un exemple qui a été pris au sérieux. En 1994, Peter Shor (AT&T) montre qu’un ordinateur quantique permet de factoriser les entiers en temps polynomial (en la taille du nombre à factoriser), alors que le meilleur algorithme connu à ce jour sur un ordinateur classique a une complexité (presque) exponentielle. Cette nouvelle a ébranlé le monde des banquiers, des militaires et des agents secrets. En effet, la plupart des algorithmes de cryptage, dont le RSA utilisé pour le code de votre carte bleue, sont fondés sur le fait qu’il est très coûteux (en temps) de factoriser des nombres entiers (ce qui rend la recherche du code trop longue pour être utilisable en pratique). Pour l’instant, il n’existe pas d’ordinateurs quantiques permettant de factoriser les nombres à plusieurs centaines de chiffres utilisés en cryptographie. Les optimistes parlent de quinze ou vingt ans, ce qui coïnciderait avec la fin de la loi de Moore. Les pessimistes pensent que des objections théoriques empêcheront de réaliser des ordinateurs quantiques de taille suffisante.
La fin de Moore ? Calculer plus vite
Nous venons d’évoquer la fin de la loi de Moore. En effet, les extrapolations de la loi de Moore indiquent que d’ici une dizaine d’années, nous aurons atteint des limites fondamentales qui ne nous permettront plus de compter sur une diminution de la taille des transistors. D’ici une dizaine d’années, les transistors seront en effet si petits que leur fonctionnement reposera sur le passage de quelques électrons.
En fait, les premiers obstacles fondamentaux ont déjà été rencontrés : la fréquence de nos processeurs n’augmente plus vraiment depuis ces dernières années. La fréquence des processeurs est corrélée avec le nombre d’opérations à la seconde que peut effectuer un ordinateur : plus la fréquence est grande, plus l’ordinateur calcule vite. Malheureusement, l’augmentation de fréquence, qui nous permet de calculer plus vite, s’accompagne aussi d’une augmentation de la puissance dissipée et on ne sait plus actuellement évacuer suffisamment efficacement la chaleur générée par le calcul.
Il y a cependant encore un moyen de calculer plus vite en gardant les mêmes machines. L’idée est la suivante : supposez que vous avez une Twingo et que vous deviez voyager plus rapidement. Vous pouvez alors acheter une Ferrari. C’est ce qu’on faisait jusqu’à présent : pour aller plus vite, on attendait le processeur de la nouvelle génération. Mais imaginez que vous ayez besoin d’aller encore plus vite. Cette fois-ci, il n’y a pas de voiture plus rapide. Alors vous décidez d’acheter deux Ferraris. L’idée n’est donc plus d’aller plus vite mais de faire plus de choses en même temps : c’est la notion de parallélisme. C’est l’approche adoptée par les constructeurs de processeurs depuis quelques années en mettant plusieurs cœurs de calcul sur la même puce.
Mais voyage-t-on vraiment plus vite avec deux voitures plutôt qu’avec une seule ? Chaque voiture n’ira pas plus vite, mais pendant que l’une parcourt une partie du trajet, l’autre peut parcourir un autre bout (à condition d’avoir deux conducteurs). Faire des choses en parallèle permet donc dans une certaine mesure d’aller plus vite : s’il faut dix hommes.ans pour construire une maison, cinq hommes pourront la construire en deux ans.
Malheureusement, cette approche a des limites : cent-vingt hommes ne pourront pas construire la maison en un seul mois. Il y a en effet des opérations qui ne peuvent pas se faire en parallèle : pour construire le toit, il faut que les murs soient présents. Et pour construire les murs, il faut que les fondations soient achevées. Ces contraintes induisent un certain ordre des opérations, ordre qui sera respecté avec la vitesse inchangée des ordinateurs.
Par ailleurs, que peut-on espérer gagner en utilisant plusieurs processeurs en parallèle pour réaliser un calcul impliquant n opérations ? Si on dispose de p processeurs, chaque processeur effectuera au mieux n/p calculs indépendants. On gagnera donc au plus un facteur constant p sur la complexité du calcul. Le parallélisme ne change donc pas la complexité intrinsèque d’un calcul, mais il « déplace les constantes », ce qui est tout de même bien utile.

Le calculateur parallèle « Blue Gene » installé au laboratoire Argonne aux U.S.A. (Photo courtesy Argonne National Laboratory) Cet ordinateur est issu de l’évolution de la génération “Deep Blue”, qui s’est rendue célèbre en battant Garry Kasparov aux échecs en 1997. En 2008, cette machine exhibait une puissance de 557 teraflops, soit 557 mille milliards d’opérations par seconde. Elle consomme un peu plus d’un megawatt, soit 350 millions d’opérations par seconde par watt. La plupart de cette énergie est en fait utilisée pour refroidir le calculateur.
Le facteur p dépend de notre technologie : c’est le nombre de processeurs qu’on peut mobiliser pour réaliser une machine parallèle. Si on relie ces processeurs de la manière la plus rapide possible (de manière à ce que les échanges de données pendant le calcul ne coûtent pas trop cher), il faut rester sur la même puce. Actuellement, on peut mettre de l’ordre de la dizaine de processeurs sur une même puce. Si on accepte de sortir de la puce, avec un réseau très rapide, p peut aller jusqu’à quelques dizaines de milliers (pour les plus gros calculateurs parallèles). Si on se contente d’un réseau plus classique, comme Ethernet qui est à la base d’Internet, on peut imaginer relier et utiliser des centaines de milliers d’ordinateurs, par exemple ceux des centres de calcul ou même ceux qui sont devant nous : c’est l’idée de grille de calcul.
Le projet SETI@home est l’un des premiers à avoir utilisé la puissance de nos ordinateurs individuels pour effectuer un calcul parallèle sur une très large échelle. L’objectif de SETI@home est de sonder les signaux électromagnétiques venus de l’espace à la recherche de régularités prouvant la présence d’une intelligence extraterrestre. Toute personne qui veut participer au projet (il y en a plus de quatre-cents mille actuellement) installe un économiseur d’écran un peu particulier sur son ordinateur. Cet économiseur d’écran, au lieu de calculer des images à afficher, se connecte au serveur de SETI@home, récupère une petite quantité de calcul à effectuer, et renvoie les résultats une fois la tâche effectuée. La puissance cumulée dédiée au projet dépasse ainsi les soixante téraflops (soixante mille milliards d’opérations élémentaires par seconde).
Le parallélisme est une histoire ancienne en informatique : certains problèmes spécialisés (la prédiction de la météorologie, les calculs en physique quantique, le décodage du génome, etc.) impliquent de grandes masses de données ou un très grand nombre d’opérations, et a poussé au développement de machines parallèles. Mais avec les limites physiques qui se rapprochent, le parallélisme se démocratise et se retrouve dans les ordinateurs qui sont devant chacun d’entre nous.
Le parallélisme reste quand même une réponse classique à la fin de la loi de Moore : on met ensemble des calculateurs existants. Une réponse moins classique est de se tourner vers d’autres technologies : peut-on calculer avec des processus chimiques, biologiques, quantiques… ? On retrouve ici des problématiques voisines de celles décrites précédemment. Nous reviendrons sur ces modèles non-conventionnels du calcul dans un article ultérieur.
L’expressivité : calculer mieux
Les exemples précédents sont motivés par le besoin d’étendre la notion de calculabilité, de changer la complexité des calculs ou encore de calculer plus vite. Ce ne sont pas les seules raisons qui poussent les informaticiens à inventer de nouveaux modèles de calcul. Une autre grande raison qui motive la recherche dans ce domaine, c’est la simplification des programmes. Grâce à la notion de calculateur universel, on peut identifier les notions de langage de programmation et de machine. Les informaticiens sont à la recherche de machines, donc de langages de programmation, qui leur permettront d’exprimer le plus simplement possible le travail à effectuer.
Un programme est un objet complexe et massif : le logiciel qui constitue un central téléphonique dépasse aujourd’hui la dizaine de millions de lignes de code. Dans les années 1980, une étude indiquait qu’un programmeur écrivait environ trois lignes de code par jour. Le reste du temps est passé à comprendre ce qu’il faut programmer, vérifier les programmes et traquer les erreurs, écrire la documentation, etc. Même si un logiciel est immatériel et peut se dupliquer pour un coût virtuellement nul, il faut comprendre que le développement d’un logiciel est coûteux en temps et en main d’œuvre humaine. Dans l’industrie des biens matériels, pour réduire les coûts, on fait appel à l’automatisation. Dans l’industrie du logiciel, rien de tel : on ne peut qu’essayer de simplifier la tâche du programmeur humain. Par exemple, on a tout intérêt à développer des langages de programmation très expressifs qui permettent de faciliter la tâche du programmeur.
Est-il possible de développer un langage de programmation (une machine) qui serait « le plus expressif possible » ? La réponse est non. Et pour une raison simple : la diversité des problèmes auxquels sont confrontés les programmes ne se laissent pas réduire à un seul langage universel qui ferait tout et du mieux possible.
Illustrons ce point. La notion de calcul développée par Alan Turing et bien d’autres conçoit un calcul comme une fonction : des données en entrée sont présentées à un calculateur qui fournit un résultat en sortie. Cette vue fonctionnelle est loin de représenter la diversité des situations que permet de traiter un ordinateur.
Considérez par exemple le navigateur web qui vous permet de lire cet article. La notion de fonction ne décrit pas bien la tâche effectuée par votre navigateur : ce programme s’exécute continuellement et ne s’arrête pas pour vous donner un résultat définitif. Au contraire, il interagit continuellement avec vous, l’utilisateur, pour répondre à vos commandes. Potentiellement, ce programme ne s’arrête jamais. Attention, cela ne veut pas dire que ce programme échappe au cadre de la calculabilité. En fait, on peut découper les tâches effectuées par votre navigateur en petits morceaux (par exemple afficher une page web à partir d’une URL) qui correspondent à des calculs au sens classique. Et l’enchaînement de deux petits morceaux correspond aussi à un calcul.
Cet exemple suggère que même si le cadre développé pour parler des calculs est toujours valide, il y a bien des situations où ce cadre n’est pas le plus adéquat : quand les programmes sont spatialement distribués dans les réseaux ; quand les programmes interagissent avec des utilisateurs, le monde physique ou bien entre eux ; etc.
Par ailleurs, imaginer de nouveaux modes de calculs et de nouveaux langages relève d’une puissance heuristique extraordinaire. C’est par exemple en s’inspirant des processus biologiques que les informaticiens ont inventé de nouvelles méthodes d’optimisation (les algorithmes évolutionnistes) ou de nouveaux processus d’apprentissage (les réseaux de neurones).
C’est pourquoi les informaticiens sont toujours à la recherche de nouveaux modèles de calcul, même si les programmes obtenus peuvent être traduits et s’exécuter sur nos ordinateurs habituels.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Louis Giavitto