
Stratégies magiques au pays de Nim
Dans le domaine des jeux les plus simples où deux joueurs s’affrontent, la théorie des jeux combinatoires, qui progresse avec régularité, est la plus abordable et la plus généreuse en jolis résultats mathématiques. Les amateurs de jeux tireront avantage de cette théorie à la fois puissante, élégante et amusante. Elle sert de socle aux développements plus subtils menés aujourd’hui pour maîtriser la programmation de jeux complexes, dont les jeux de tableaux comme les Dames, les Échecs et le Go. Un jeu à deux joueurs entre dans la catégorie des jeux combinatoires s’il vérifie les conditions suivantes :
- Les deux joueurs jouent à tour de rôle.
- Toutes les informations concernant le jeu — configurations, possibilités de mouvements des joueurs – sont connues à chaque instant des deux joueurs (l’information est complète).
- Aucun hasard n’intervient dans le jeu (pas de lancer de dé, ni de distribution aléatoire de cartes, etc.).
- Dans la version normale du jeu, le joueur qui n’a plus aucune possibilité de mouvement perd la partie. Lorsque la convention inverse est adoptée (dans la
version « misère » ou « qui perd gagne » du jeu), celui qui fait le dernier mouvement perd.
Deux types de jeux combinatoires sont particulièrement bien compris et disposent de théories détaillées et puissantes : les jeux de Nim, entièrement résolus en 1901 par le mathématicien américain Charles Bouton, et les jeux impartiaux où le théorème de Sprague-Grundy, qui en donne une compréhension générale, est devenu d’usage courant pour écrire des programmes informatiques. Nous allons présenter ce noyau fondamental de la théorie à l’aide d’exemples simples qui vous permettront de briller en société en gagnant d’une manière qui semblera magique à vos adversaires.
Les jeux de Nim


Machine Nimrod spécialisée dans le Nim, construite par la Société Ferranti et présentée en 1951 à Londres.
La stratégie gagnante du jeu de Nim fait intervenir la numération binaire et se prête à la programmation ou même à la construction de dispositifs électroniques qui jouent parfaitement au jeu de Nim. Très tôt, des programmes et des machines spécialisées ont été conçus pour jouer – et gagner – au jeu de Nim. La machine Nimrod fut construite par la Société Ferranti et présentée en 1951 à Londres. Cette machine spécialisée dans le Nim n’était pas un ordinateur complet, car celui que Ferranti avait prévu d’exposer n’avait pas pu être mis au point à temps, et en réalité la machine Nimrod ne savait jouer qu’au jeu de Nim ! Sa présentation fut un grand succès : comme le raconte un témoin de l’époque, ce qui intéressait le public n’était pas de jouer contre la machine, mais les impressionnantes séries de lampes clignotantes dont elle était équipée et qui matérialisaient son activité pensante !
Quelques liens (en anglais) :
Sous diverses formes, ces jeux semblent avoir été pratiqués en Europe dès le XVIe siècle et même avant, en Chine. Bouton les baptisa du nom de Nim sans que nous sachions si Nim provient de l’allemand Nimm qui signifie prendre, du verbe de l’ancien anglais Nim qui avait le même sens, ou si c’est une astuce graphique puisqu’en retournant NIM, on obtient le mot anglais WIN qui signifie gagner. Ce jeu tient une place importante dans l’intrigue du film d’Alain Resnais L’année dernière à Marienbad avec Delphine Seyrig, film qui obtint le Lion d’or de la Mostra de Venise en 1961. On peut voir les extraits du film où les personnages « jouent » la version misère en anglais.
Les règles sont les suivantes : p lignes d’allumettes (ou de pions) sont disposées devant les joueurs et comportent respectivement N1 allumettes, N2 allumettes, …, Np allumettes.
Les joueurs jouent à tour de rôle et chacun des deux joueurs prend autant d’allumettes qu’il veut dans une ligne (mais au moins une). Celui qui prend la dernière allumette a gagné. Dans la version « misère », celui qui prend la dernière allumette a perdu.
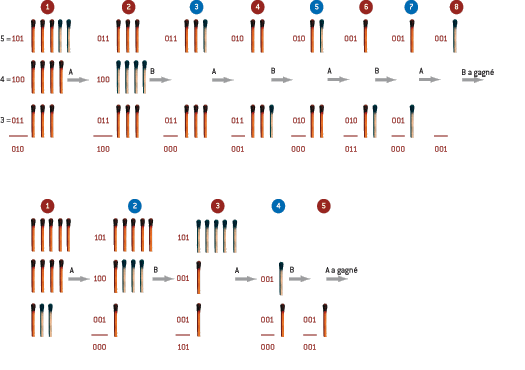
Chaque joueur joue à tour de rôle en prenant autant d’allumettes qu’il le veut dans une ligne ; le joueur qui prend la dernière allumette gagne.
Dans la partie figurée en haut, le joueur B gagne, alors que le joueur A avait une position gagnante initiale. Cette position gagnante est indiquée par une somme de Nim non nulle des nombres d’allumettes des lignes (exprimés en numération binaire). D’une position gagnante, un joueur peut toujours amener son adversaire dans une position perdante à somme de Nim nulle. Les numéros des positions gagnantes sont en rouge, ceux des positions perdantes en bleu.
La partie figurée en bas est correctement jouée par A.
L’analyse de ce jeu par Bouton l’a conduit à énoncer un théorème inattendu. Celui-ci indique que le joueur qui doit jouer dispose d’une stratégie gagnante de jeu si les entiers (N1, N2, …, Np) qui décrivent la position du jeu ont une somme non nulle, pour une addition particulière nommée la Nim-addition. Cette Nim-addition, que l’on retrouvera dans le théorème de Sprague-Grundy et dans toute la théorie des jeux combinatoires, est simple dès que les entiers N1, N2, …, Np sont écrits en base de numération binaire. Expliquons cette addition bizarre à partir d’un exemple :
N1 = 11, N2 = 9, N3 = 7.
Écrire un nombre en binaire revient à décomposer ce nombre en une somme de
puissances de 2 : 1, 2, 4, 8, 16, 32, …. Puisque 11 = 8 2 1, l’écriture binaire de 11 est 1011, ce qui signifie 1 fois 8, 0 fois 4, 1 fois 2, 1 fois 1. De même 9 = 8 1 = 1001 et 7 = 4 2 1 = 111.
La Nim-addition consiste à disposer les chiffres binaires comme on le fait quand on pose une addition habituelle, puis à additionner en colonnes, sans tenir compte des retenues. Le nombre binaire obtenu retraduit en entier est le résultat :
| 1 0 1 1 | (11) | ||
| 1 0 0 1 | (9) | ||
| 1 1 1 | (7) | ||
| ––––––––––– | |||
| = | 0 1 0 1 | (5) | |
Notons bien que nous travaillons en base 2 : 1 1 = 10, 1 1 1 = 11 et, puisque nous ne tenons pas compte des retenues, 1 1 = 0, 1 1 1 = 1. Le fait de négliger les retenues a pour conséquence que le chiffre résultat de la somme d’une colonne vaut 0 quand il y a un nombre pair de 1 dans la colonne, et vaut 1 quand il y a un nombre impair de 1 dans la colonne. Pratiquer la Nim-addition est simple dès lors que l’on sait décomposer en binaire et que l’on sait repérer les nombres pairs et impairs. La Nim-addition de la configuration (11, 9, 7) est 5. D’après le théorème de Bouton, c’est une configuration gagnante. Si c’est à vous de jouer, vous disposez d’une stratégie de jeu gagnante qui consiste à placer votre adversaire en position perdante (c’est-à-dire ayant une Nim-addition nulle). Ici, il faut prendre 5 allumettes dans le troisième paquet, c’est-à-dire placer l’adversaire en position (11, 9, 2), dont la Nim-addition est 0 :
| 1 0 1 1 | (11) | ||
| 1 0 0 1 | (9) | ||
| 1 0 | (2) | ||
| ––––––––––– | |||
| = | 0 0 0 0 | (0) | |
Facile à dire ! Mais en pratique, comment faire avec des lignes d’allumettes ? Ce n’est pas très compliqué et, avec un petit entraînement, on peut opérer de tête les calculs nécessaires. Voici la méthode. Pensez les nombres en les séparant en paquets ayant chacun un nombre d’allumettes qui est une puissance de 2. Comme nous venons de l’expliquer, cela revient à les écrire en numération binaire. Faites ce travail de tête ou déplacez légèrement les allumettes pour matérialiser ces décompositions. Partant de la disposition :
| I I I I I I I I I I I | (11) | |
| I I I I I I I I I | (9) | |
| I I I I I I I | (7) |
vous obtenez — discrètement — la disposition :
| I I I I I I I I | I I | I | (11 = 8 2 1) | |||||
| I I I I I I I I | I | (9 = 8 1) | ||||||
| I I I I | I I | I | (7 = 4 2 1) |
Il est facile maintenant de voir si oui ou non il y a un nombre pair de paquets dans chaque colonne. Si c’est le cas, vous ne gagnerez pas face à un adversaire averti, car vous êtes en situation perdante. Sinon, il existe une façon de jouer qui conduit à une configuration dont chaque colonne contient un nombre pair de paquets. Ici, on voit immédiatement qu’il faut enlever le paquet I I I I de la dernière ligne, ainsi que le paquet I, c’est-à-dire 5 allumettes au paquet qui en contient 7. C’est d’ailleurs la seule façon de jouer qui, ici, conduise à une configuration nulle. Exercez-vous avec (13, 10, 3, 1).
| I I I I I I I I | I I I I | I | (13) | |||||
| I I I I I I I I | I I | (10) | ||||||
| I I | I | (3) | ||||||
| I | (1) |
Il faut enlever I I I I et I de la première ligne, c’est-à-dire passer à la position (8, 10, 3, 1).
Reste une double question. Pourquoi le théorème de Bouton est-il vrai, c’est-à-dire :
(a) Pourquoi, en opérant comme on vient de l’indiquer à partir d’une situation dont la Nim-addition est non nulle, on finit par gagner ?
(b) Pourquoi, si vous vous trouvez dans une position nulle, vous perdrez face à un adversaire qui connaît et applique la règle de la Nim-addition ?
L’idée de la démonstration se fonde sur les deux faits suivants. D’une part, à partir d’une situation nulle, quoi que vous jouiez, vous créez une situation non nulle ; d’autre part, à partir d’une situation non nulle, il existe toujours au moins une façon de jouer qui mène à une situation nulle. Il en résulte qu’une fois tombé dans une situation nulle, un joueur n’en sort jamais si son adversaire fait ce qu’il faut, et cela jusqu’à ce qu’il se trouve dans la situation nulle de la fin de partie (il n’y a plus aucune allumette) qui signifie qu’il a perdu !
Toutes sortes de variantes du jeu de Nim classique ont été envisagées et résolues. La première est la variante « misère » : on y convient que le joueur qui prend la dernière allumette perd. La solution est la suivante : vous jouez comme dans le jeu normal en appliquant la règle de Bouton, sauf si votre coup conduit à une situation où il ne reste que des paquets d’une seule allumette, auquel cas vous jouez de façon à laisser un nombre impair de paquets d’une allumette (au lieu d’en laisser un nombre pair, ce que le théorème de Bouton vous soufflerait). Bien sûr, dès lors, vous êtes certain de gagner. Cette solution est un peu étonnante puisqu’elle signifie que partant par exemple de (11, 9, 7), le joueur qui commence est certain de gagner, que ce soit la règle normale qui détermine le gagnant ou que ce soit la règle misère. Il jouera exactement les mêmes coups, sauf par exemple quand arrivé à (1, 1, 3) qui l’aurait conduit à jouer (1, 1), il choisira de jouer (1, 1, 1) pour le jeu misère.
La variante de Moore
Une généralisation du jeu de Nim, notée Nimk, étudiée et résolue par le mathématicien Eliakim Moore (1862-1932), consiste à autoriser les joueurs à prendre non pas des allumettes dans un paquet unique, mais dans plusieurs paquets, pourvu qu’ils n’en prennent pas dans plus de k paquets (k fixé) et pourvu qu’ils en prennent au moins une. Le jeu de Nim est Nim1 ; dans une partie de Nim2, chaque joueur prend à chaque coup autant d’allumettes qu’il veut dans un ou deux paquets (et en prend au moins une), etc. La solution de Moore généralise celle de Bouton. On procède de la même manière (décomposition en binaire de chaque nombre définissant une configuration du jeu), sauf qu’au lieu d’effectuer une somme sans retenue en base 2 sur les colonnes, on l’effectue en base k 1.
Si le résultat est nul, c’est que la situation est perdante, sinon elle est gagnante et la stratégie de jeu consiste à créer une situation nulle pour son adversaire et à l’y maintenir de coup en coup. Par exemple pour k = 2, en partant de la position de notre exemple :
| 1 0 1 1 | (11) | |||
| 1 0 0 1 | (9) | |||
| 1 1 1 | (7) | |||
| ––––––––––– | ||||
| = | 2 1 2 0 | non nulle | ||
Pour que le nombre de 1 de chaque colonne soit un multiple de 3 (k 1 = 3),
on choisit d’agir sur les deux premiers paquets. On est conduit à la position (7, 7, 7).
| 1 1 1 | (7) | |||
| 1 1 1 | (7) | |||
| 1 1 1 | (7) | |||
| ––––––––––– | ||||
| = | 0 0 0 | nulle | ||
L’adversaire créera en jouant une configuration non nulle à partir de laquelle vous le mettrez dans une position nulle, etc.
Paquets infinis d’allumettes !
Les jeux finis sont certes amusants, mais le propre des mathématiques est de considérer l’infini avec le plus grand sérieux et donc… d’inventer des jeux qui l’utilisent ! Le jeu de Nim (normal) se pratique en partant d’une série de paquets d’allumettes comportant chacun un nombre fini d’allumettes. Et si on acceptait des paquets infinis ? Georg Cantor a introduit une catégorie de nombres infinis, les ordinaux, qui vont faire l’affaire et qui garantiront que toute partie se termine par un gagnant ou un perdant. Rappelons que pour construire les ordinaux, on convient qu’au-delà de tous les entiers 0, 1, 2, …, n, … on trouve un nombre plus grand que tous les autres, noté ω (oméga) et dénommé « le premier ordinal transfini ». On convient aussi qu’il y un ordinal juste au-dessus de lui, ω 1, et un autre juste au-dessus encore ω 2, puis ω 3, ω 4, etc. Au-delà de tous ces nombres transfinis, il y a 2ω (divers types de notations sont possibles, nous choisissons celle-ci qui est naturelle). Il y a aussi 2ω 1, 2ω 2, 2ω 3,…, 3ω, 3ω 1, 3ω 2,…, 4ω,… et juste après tous ces nω, il y a ω2. Nous nous contenterons de ces ordinaux, mais tout ce qui suit se généralise aux ordinaux au-delà de ω2 (et il y en a beaucoup !).
Une situation du jeu de Nim infini est une série de paquets d’allumettes ayant chacun un nombre d’allumettes représenté par un ordinal jusqu’à ω2. Par exemple : (ω 5, ω2, 2ω 1, 9ω, 7)
Jouer consiste à prendre des allumettes dans un paquet, c’est-à-dire à remplacer l’ordinal désignant le paquet d’allumettes par un ordinal plus petit. Par exemple, on pourra à partir de la configuration décrite ci-dessus, prendre des allumettes dans le deuxième paquet (le plus gros) et y laisser 5ω 1 allumettes, ce qui donnera la configuration : (ω 5, 5ω 1, 2ω 1, 9ω, 7).
Un tel jeu est-il assuré de se terminer ? Cela ne semble pas évident puisqu’il y a une infinité d’allumettes dans certains paquets. Pourtant, on peut montrer que toute partie a nécessairement une durée finie. Il est impossible de dire que la durée d’une partie est inférieure à n étapes (n étant un entier fixé), mais aucune partie ne peut se prolonger indéfiniment.
Comment gagner au Nim infini ?
En jouant quelques parties, vous découvrirez qu’avec ces paquets infinis, il y a aussi des configurations qui assurent de gagner, et d’autres qui ne permettent pas de battre un adversaire malin. Il est clair par exemple que (ω, 12) est une situation gagnante : il faut jouer (12, 12). De même, pour tout entier n, (ω, n) est gagnante. En revanche, (ω, ω) est perdante car, quoi que vous fassiez, votre adversaire pourra répliquer en vous plaçant dans une configuration (n, n) qui est perdante (elle a une Nim-addition nulle). De proche en proche, on remarque ainsi que (ω, ω, ω) est gagnante, (ω, ω, ω, ω) est perdante, etc. Comment faire dans le cas général ? Voici la règle qui généralise le théorème de Bouton. Énonçons-la d’abord sans prendre en compte ω2. La configuration (a1ω b1, a2ω b2,…, akω bk) est perdante si la Nim-addition des ai est nulle ainsi que la Nim-addition des bi. S’il y a en plus des ω2, la configuration est perdante si leur nombre est pair. Dans tous les autres cas, la configuration est gagnante et bien sûr la stratégie gagnante consiste à mettre l’adversaire dans une situation perdante et à l’y maintenir de coup en coup.
Jeux impartiaux
Venons-en au théorème magique de Sprague-Grundy (découvert indépendamment par R. Sprague en 1935 et par P. Grundy en 1939). Il concerne la catégorie de jeux combinatoires nommée jeux impartiaux. Ces jeux sont semblables au jeu de Nim normal :
- Les coups permis à un joueur ne dépendent que de la configuration.
- Le but est de placer l’adversaire dans une position où il ne peut plus jouer.
- Les règles du jeu sont telles qu’il n’y a pas de partie nulle ou qui se prolonge indéfiniment.
Un exemple de jeu impartial fini est le jeu du déplacement d’un pion sur un graphe sans cycle : il va nous guider pour expliquer le théorème. Un pion est placé sur le nœud d’un graphe donné qui ne doit pas comporter de cycle (on ne doit pas y trouver de suite d’arcs formant une boucle). Chaque joueur déplace, à son tour, le pion en suivant un arc du graphe. Le joueur qui ne peut plus déplacer le pion a perdu.
Les jeux impartiaux sont tous équivalents à des jeux de déplacement de pions sur un graphe sans cycle (c’est-à-dire sans possibilité de tourner en rond). Un pion est placé sur un nœud du graphe du jeu et, à tour de rôle, les joueurs le font avancer en suivant les arcs orientés du graphe. Lorsque plusieurs arcs du graphe partent du nœud où est posé le pion, le joueur a plusieurs possibilités de jeu. Lorsque plus aucun arc ne part du nœud où est posé le pion, celui-ci est bloqué. Le premier joueur qui ne peut plus jouer a perdu.
Le jeu se pratique aussi avec plusieurs pions sur le même graphe (on parle alors de jeux simultanés ou de somme de jeux) : le joueur qui ne peut plus bouger aucun pion a perdu. Dans la règle avec plusieurs pions, on n’interdit pas la présence de plusieurs pions sur un même nœud.
Le théorème de Sprague-Grundy indique que pour gagner à de tels jeux avec un ou plusieurs pions, il faut commencer par marquer chaque nœud du graphe par un entier (dénommé nimber) qu’on obtient par la méthode suivante :
- Les nœuds correspondant à un blocage du pion sont marqués par un 0.
- De proche en proche, on marque chaque nœud N par l’entier le plus petit qui n’apparaît pas dans les nœuds accessibles à partir de N. Si, par exemple, à partir de N, on peut accéder à des nœuds marqués 0, 1, 3, le nœud N sera marqué 2. C’est la règle du mex (minimum exclu).
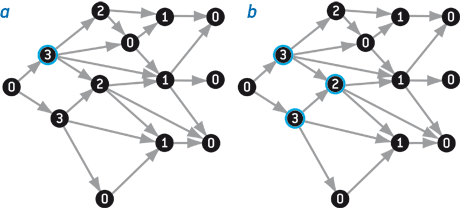
Le théorème de Sprague-Grundy indique comment gagner. Jeu avec un seul pion : pour gagner, il faut mettre le pion sur un nœud de nimber 0. Une fois qu’on a réussi, on est certain de toujours pouvoir répliquer à un coup de l’adversaire en le remettant sur un nœud de nimber 0. Jeu avec plusieurs pions : pour gagner, il faut mettre l’adversaire dans une position telle que la nim-addition des nimbers des cases occupées soit nulle. Là encore, une fois l’adversaire placé dans une telle position, on est certain de pouvoir toujours le remettre dans une telle position en réponse à ce qu’il jouera.
Dans l’exemple a (jeu avec un seul pion), le joueur à qui c’est le tour doit déplacer le pion vers le nœud marqué 0. Dans l’exemple b (jeu avec trois pions), le joueur à qui c’est le tour doit bouger le pion qui est sur le nœud de nimber 2 et le placer sur le nœud à droite (de nimber 0). La position de son adversaire sera alors constituée de trois pions de nimber 3, 3 et 0. La nim-addition de ces trois nombres est nulle, l’adversaire aura donc perdu.
Voici maintenant le théorème de Sprague-Grundy qui comporte trois volets :
- Chaque position d’un jeu impartial fini est équivalente à un jeu de Nim avec un seul paquet dont le nombre d’allumettes est un entier ; ce nombre est nommé le nimber de la position.
- Le calcul du nimber d’une position se fait par la règle du mex (minimum de la valeur exclue) : les positions finales ont pour
nimber 0 ; le nimber d’une position permettant d’atteindre les positions de nimber n1, n2, …, nk est le plus petit entier qui n’est pas dans la liste n1, n2, …, nk. - Lorsque l’on joue simultanément à plusieurs jeux impartiaux (jeu 1, jeu 2, …, jeu m), le nimber de la position définie comme la combinaison de la position P1 du jeu 1, P2 du jeu 2, …, Pm du jeu m, est la Nim-addition des nimbers des positions P1, P2, …, Pm.
Le théorème magique
Cela semble un peu difficile à avaler, mais en pratique c’est très simple. Reprenons l’exemple du pion sur un graphe (auquel tout jeu impartial fini peut d’ailleurs se ramener si on veut). Il nous montrera l’immense intérêt pratique de ce théorème. Pour savoir comment jouer quand un pion est placé sur le graphe, la méthode consiste à calculer le nimber de chaque nœud du graphe. Grâce à la règle du mex, c’est l’affaire de quelques secondes pour chaque nœud du graphe. Pour jouer et gagner, la méthode est de tenter de placer votre adversaire dans une position dont le nimber est 0, et dès que c’est fait, maintenez-le toujours dans des positions de nimber 0. Si vous êtes dans une position dont le nimber est non nul, c’est possible, sinon c’est impossible et vous devez espérer que votre adversaire n’a pas connaissance du théorème de Sprague-Grundy. Comme dans le jeu de Nim, une fois dans une position de nimber 0, quoi que fasse votre adversaire, vous pourrez toujours le remettre dans une position de nimber 0.
La troisième partie du théorème concerne les jeux simultanés (on dit aussi les « sommes de jeux »). Au lieu de placer un pion sur le graphe, placez-en plusieurs. La règle est que chaque joueur déplace un pion qu’il choisit librement (toujours en suivant un arc du graphe bien sûr). Le joueur qui ne peut plus déplacer aucun pion a perdu.
Grâce au théorème de Sprague-Grundy, nous allons analyser et résoudre le jeu suivant, ce qui serait pratiquement impossible autrement. Sur un damier 5×5, on place cinq pions sur la colonne de gauche. Un pion peut bouger d’une ou deux cases vers la droite ou d’une ou deux cases vers le bas à chaque coup. Les joueurs jouent à tour de rôle en déplaçant un pion. Plusieurs pions peuvent se trouver sur une même case. Tous les pions finissent par se retrouver sur la case en bas à droite. Le premier joueur qui ne peut plus jouer (parce que tous les pions sont arrivés sur cette case) a perdu.
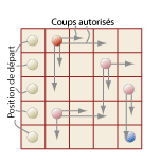
Comment gagner ?
Solution. On calcule le nimber de chaque case en utilisant la règle du mex qui permet de remplir le tableau progressivement de la droite vers la gauche. Pour la colonne de gauche, on a trouvé les nimber 0, 1, 3, 0, 1 dont la Nim-addition est 3. Le joueur qui commence dispose donc d’une stratégie gagnante. Son premier coup doit amener son adversaire dans une position ayant une Nim-addition nulle. Il peut par exemple avancer le pion de la troisième ligne de deux cases.
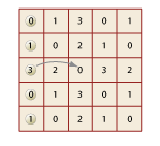
Le théorème de Sprague-Grundy formule une méthode magique pour gagner. À chaque ensemble de pions sur le graphe correspond un nimber. Pour le connaître, il suffit de faire la Nim-addition des nimbers des nœuds où sont placés les pions. Si le résultat est non nul, vous êtes certain de gagner, la stratégie consistant à déplacer un pion de telle façon que la Nim-addition des cases qu’occuperont les pions après votre déplacement soit toujours nulle. D’une manière tout à fait générale, le théorème de Sprague-Grundy fournit le moyen de calculer les nimbers de tout jeu impartial (par la règle du mex) et un moyen très rapide et efficace de calculer les nimbers associés à des positions d’un jeu simultané.
L’intérêt des jeux simultanés est qu’un jeu peut parfois se décomposer en une somme de jeux simultanés plus simples. C’est le cas de la fin des parties au jeu de Go quand plusieurs actions se déroulent indépendamment sur le goban. C’est le cas aussi du Jeu des Pousses (voir la rubrique « Logique et calcul » de la revue Pour la Science de septembre 2008) où des sous-jeux indépendants apparaissent, dont la méthode des nimbers permet la résolution rapide. Comme la règle du mex est facile à programmer, une méthode efficace de programmation des jeux impartiaux doit se fonder sur le calcul du nimber en utilisant la règle du mex et, à chaque fois que possible, la troisième partie du théorème de Sprague-Grundy (c’est la méthode utilisée par Julien Lemoine et Simon Viennot qui leur a permis de battre tous les records au Jeu des Pousses).
Ce que nous venons d’expliquer pour les jeux impartiaux finis s’adapte aux jeux impartiaux infinis à condition de généraliser la notion de nimber et d’accepter que n’importe quel ordinal — et non plus n’importe quel entier — soit un nimber. L’opération mex, qu’on étend immédiatement aux ordinaux, donne alors la méthode pour attribuer un nimber (fini ou infini) à chaque position d’un jeu impartial infini. L’opération d’addition que nous avons définie (partiellement) pour les ordinaux donne de son côté la méthode pour traiter les jeux impartiaux infinis simultanés.
On recommande aux enfants de ne pas jouer avec des allumettes. Pour les mathématiciens, le conseil inverse s’impose.
Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°377, en mars 2009.
- J. Lemoine et S. Viennot, Glop : Combinatorial Games Solver.
- J. Lemoine et S. Viennot, A further computer analysis of sprouts, 15 p., 2007, disponible en PDF (188 Ko).
- Thomas Ferguson, Games Theory, part I. Impartial Combinatorial Games, 46 p., 2005, disponible en PDF (360 Ko).
- E. R. Berlekamp, J. H. Conway et R. K. Guy, Winning Ways for your Mathematical Plays, Ac. Press 1982 (nouvelle édition : A. K. Peter, 2003).
- J. H. Conway, On Numbers and Games, Ac. Press, 1976 (nouvelle édition : A. K. Peter, 2000).
- P. M. Grundy, Mathematics and games, Eureka, vol. 2, pp. 6-8, Eureka, vol. 27, pp. 9-11, 1939.
- R. K. Guy, Impartial Games, Games of No Chance, MSRI Publications 29, R. Nowakowski ed., Cambridge Univ. Press., 1996.
- E. H. Moore, A generalization of a game called Nim, Ann. Math., vol. pp. 11, 93-94, 1910.
- C. L. Bouton, Nim, a game with a complete mathematical theory, Ann. Math., vol. 3, pp. 35-39, 1902.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).