
Turing à l’assaut d’Enigma
Dès l’Antiquité, généraux et souverains ont rivalisé d’ingéniosité pour imaginer des techniques d’espionnage toujours plus créatives, mais aussi des procédés sophistiqués pour protéger le secret de leurs communications. Les mathématiciens ont alors régulièrement été mis à contribution au sein des fameux « cabinets noirs » pour décrypter les messages chiffrés ennemis, œuvrant à l’apparition d’une science nouvelle, la « cryptanalyse ». Il n’est donc pas surprenant que, dès le début de la seconde guerre mondiale, les services de renseignement britanniques aient fait appel au jeune Alan Turing, brillant mathématicien, pour travailler au décryptage des messages allemands.
Plusieurs alphabets pour un message
Depuis les années vingt, l’armée allemande s’est équipée d’une machine à chiffrer révolutionnaire, la machine Enigma.
Inventée en 1919 par Arthur Scherbius et destinée, à l’origine, à une utilisation commerciale, la machine Enigma est utilisée par l’armée allemande durant la seconde guerre mondiale pour chiffrer les messages. Mais dès les années trente, les Polonais puis les Anglais se dotent de spécialistes capables de décrypter les messages secrets ennemis. Cette guerre du chiffre entraîna des perfectionnements de la machine. Ainsi une version plus complexe causa des problèmes aux services secrets britanniques qui, pendant plusieurs mois, eurent des difficultés pour déchiffrer les messages codés.
La capture, en 1942, d’un U-boot (sous-marin) allemand avec à son bord une machine Enigma et des documents sur l’utilisation des codes secrets permirent aux alliés de connaître les positions de sous-marins et de réduire le tonnage des navires coulés. Si pendant toute la guerre, les Allemands ont été persuadés de l’inviolabilité de leurs communications, cette guerre du chiffre a sans nul doute contribué à la victoire des alliés.

Soldats allemands utilisant une machine Enigma. Sur cette photographie datant de la seconde guerre mondiale, des soldats allemands utilisent une machine Enigma qui permettait d’envoyer des messages secrets. En réalité, alors que les Allemands étaient persuadés que leurs communications étaient inviolables, leurs messages étaient interceptés et décryptés par les alliés.
Photo © SSPL/Leemage.
Jusqu’à cette époque, la plupart des méthodes de chiffrement étaient des variantes de la substitution alphabétique. Une substitution alphabétique consiste à remplacer chaque lettre de l’alphabet par une autre : par exemple, chaque « a » devient « k », chaque « b » devient « z », chaque « c » devient « u »… Le nouvel alphabet utilisé (dans notre exemple « kzu… ») est le secret partagé par l’expéditeur et le destinataire. Cependant, depuis le IXe siècle, on sait décrypter un tel système en calculant la fréquence d’apparition dans le message chiffré de chaque lettre (puis de chaque groupe de deux ou trois lettres) et en la comparant à la fréquence des lettres dans la langue d’origine. Ainsi, pour un message initial en français, la lettre apparaissant le plus souvent dans le message chiffré correspond très certainement au « e ».
Pour parer cette attaque, on utilisait des substitutions polyalphabétiques : les lettres du message étaient chiffrées avec des alphabets différents. Mais pour que le procédé reste utilisable, le nombre d’alphabets restait limité. Par exemple, on utilisait quatre alphabets secrets, le premier servait à chiffrer les lettres en positions 1, 5, 9… le deuxième les lettres en positions 2, 6, 10… L’attaque par analyse de fréquence ne s’applique alors plus directement. Toutefois, il suffit de regrouper les lettres du message chiffré obtenues avec le même alphabet et d’analyser les fréquences indépendamment dans chacun de ces groupes. L’attaque est simplement un peu plus difficile, car la longueur de texte disponible pour l’analyse est divisée par le nombre d’alphabets, mais ce dernier reste relativement petit. C’est ainsi que la plupart des chiffrements conçus jusqu’à la fin de la première guerre mondiale ont pu être attaqués.
L’électromécanique au service du secret
L’innovation majeure d’Enigma est d’utiliser un procédé électromécanique pour engendrer un nombre considérable d’alphabets ; le nombre de lettres chiffrées avec le même alphabet devient alors tellement petit que les fréquences d’apparition ne sont plus du tout significatives.
À première vue, Enigma, avec son clavier, ressemble à une machine à écrire portative. Mais il s’agit d’une machine à chiffrer, c’est-à-dire d’une machine à coder des messages, conçue en 1919 par Arthur Scherbius. Différentes variantes ont été utilisées par l’armée allemande pendant la seconde guerre mondiale.
Lorsqu’on tape une lettre sur le clavier, c’est une autre lettre qui s’éclaire sur le tableau lumineux. Entre les deux, il y a tout un mécanisme, composé de rotors et de câbles électriques. Chaque fois qu’une lettre est chiffrée, cela entraîne la rotation d’un des rotors. La même lettre sera donc chiffrée différemment la prochaine fois. Ce système est rendu plus complexe encore par l’ajout d’un tableau de connexions. Pour une machine à trois rotors, il y a ainsi plusieurs centaines de milliards de milliards de possibilités.

Une des machines Enigma, machines électromécaniques qui servaient à chiffrer et à déchiffrer des messages notamment grâce à trois rotors et à un tableau de connexions. Cette machine à écrire n’est pas ordinaire. Enigma servit bien à écrire… mais des messages codés ! Elle fut utilisée pendant la seconde guerre mondiale par l’armée allemande pour crypter ses messages.
Photo © SSPL/Leemage.
Enigma se présente comme une machine à écrire, avec un clavier sur lequel on tape successivement les lettres du message de départ, non chiffré, et un tableau lumineux où s’allument les lettres chiffrées correspondantes. Il suffit de recopier les lettres éclairées pour obtenir le message chiffré.
Les trois figures présentées ci-dessous représentent la machine en réduisant le nombre des 26 lettres de l’alphabet à 6 pour simplifier la lecture des schémas.
L’alphabet de substitution est défini par le câblage électrique d’un rotor. Ainsi, sur la machine à 6 lettres de la figure ci-dessous, « a » est transformé en « c », « b » en « d »…
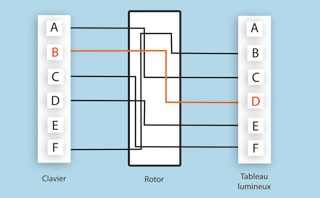
Machine à rotor unique : chiffrement d’une lettre avec une machine à un rotor.
Après avoir chiffré la première lettre, l’alphabet de substitution est modifié en faisant tourner le rotor d’une position. Dans le nouvel alphabet, « b » est maintenant transformé en « e ». En faisant tourner le rotor après le chiffrement de chaque lettre, Enigma ne revient au premier alphabet qu’après 26 lettres.
Comme ce nombre d’alphabets est encore trop faible pour éviter les attaques par analyse de fréquence, Enigma utilise trois rotors en parallèle : à chaque fois que le premier rotor a fait un tour complet, on avance le second rotor d’une position. Le troisième rotor, lui, ne bouge que quand le deuxième a aussi fait un tour complet. Par ce procédé, on utilise donc 263 = 17 576 alphabets différents, ce qui rend l’analyse de fréquence hors de portée.
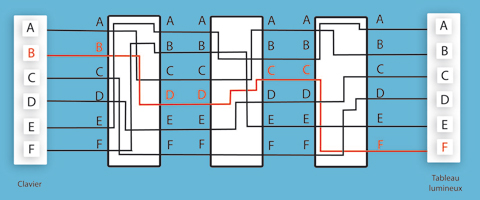
Machine à trois rotors.
Pour utiliser une telle machine à chiffrer, une des difficultés pratiques vient du fait qu’il est indispensable de disposer de deux machines différentes : l’une pour chiffrer, l’autre qui correspond à la transformation inverse, pour déchiffrer. Pour pallier cet inconvénient, son concepteur, Arthur Scherbius, eut l’idée d’ajouter un réflecteur, similaire à un rotor fixe. Son rôle est de transformer la lettre obtenue après passage dans les trois rotors puis de faire subir au résultat la même transformation dans le sens inverse. Le résultat du chiffrement d’une lettre correspond ainsi à un circuit entre une lettre du clavier et une lettre du panneau lumineux.
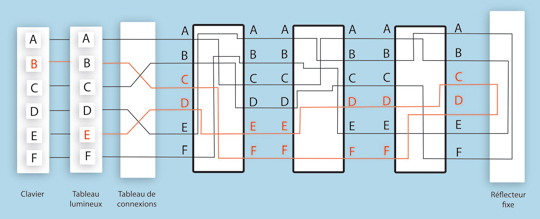
Machine à trois rotors avec réflecteur et tableau de connexions.
Une machine à chiffrer et à déchiffrer
Comme c’est ce même circuit qui est utilisé pour déchiffrer, on voit que si la lettre « b » est chiffrée en « e », alors pour une position identique des rotors, la lettre « e » sera chiffrée en « b ». Grâce à cette astuce, une seule machine suffit à chiffrer et à déchiffrer, car il s’agit exactement de la même transformation. Les rotors doivent avoir la même position de départ pour le chiffrement et pour le déchiffrement ; cette position fait partie du secret partagé par l’expéditeur et le destinataire.
Avec l’étrange conception d’un hasard visiblement bien ordonné, l’armée allemande poussa cependant le raffinement jusqu’à choisir un réflecteur qui ne transformait aucune lettre en elle-même, assurant ainsi qu’une lettre ne pouvait jamais être son propre chiffré. Loin d’être une garantie de sécurité supplémentaire, cette propriété fut amplement exploitée par Alan Turing dans sa cryptanalyse !
Si l’on suppose que le câblage des rotors est connu de l’attaquant (ce qui fut le cas, car les plans de la machine furent communiqués aux Français par un espion dès le début des années trente), la sécurité d’Enigma repose sur un triple secret. La position de départ des trois rotors offre 263, soit 17 576 possibilités, le choix de ces trois rotors parmi cinq rotors différents multiplie ce nombre de clés possibles par 10, enfin l’ordre des rotors le multiplie par factorielle de 3, soit 3 ! = 1 × 2 × 3 = 6. Le nombre de clés possibles était donc 263 × 10 × 6, ce qui fait plus d’un million de clés à essayer.
Pour augmenter encore ce nombre, Arthur Scherbius avait ajouté un tableau de connexions dont le rôle est de transposer 10 paires de lettres immédiatement en sortie du clavier et avant affichage sur le tableau lumineux (cf. la figure où cela est représenté sur 2 paires de lettres). Le choix de ces dix couples faisait partie de la clé secrète, multipliant ainsi le nombre de possibilités par 1014, ce qui conduit à un nombre total de presque 1020 clés, c’est-à-dire des centaines de milliards de milliards. Les passer en revue de nos jours prendrait encore plusieurs mois, même avec un très grand nombre de nos ordinateurs.
Premiers pas vers la résolution de « l’Enigma »
Les premiers travaux de cryptanalyse de la machine Enigma ont été réalisés par des mathématiciens polonais, notamment Marian Rejewski, avant le début de la guerre. Leur attaque reposait sur une technique encore utilisée très fréquemment en cryptanalyse : la stratégie « diviser pour mieux régner ». Il s’agit de diviser le secret en deux parties (ici les rotors et le panneau de connexions) et de trouver un moyen de tester une de ces parties (par exemple, la position de départ des rotors) indépendamment de l’autre. Pour cela, Marian Rejewski exploitait la connaissance de quantité de couples correspondant à deux versions chiffrées d’une même lettre à trois positions d’écart. Ces couples étaient obtenus car chaque communication allemande débutait par la transmission d’une nouvelle clé de trois lettres, qui était toujours répétée afin d’éviter les erreurs. Mais en 1939, peu de temps avant l’invasion de la Pologne, l’armée allemande décida de complexifier Enigma (en augmentant le nombre de rotors possibles et le nombre de transpositions dans le panneau de connexions), puis cessa de répéter les clés, rendant impossible l’attaque de Marian Rejewski.
Bletchley Park
Les cryptanalystes polonais eurent néanmoins le temps de transmettre leurs travaux aux services de renseignement britanniques, qui lancèrent dans le plus grand secret l’opération dite « Ultra » pour décrypter les messages d’Enigma. Ces travaux étaient menés par une équipe de sept mille personnes, où Alan Turing se distingua.
Mathématiciens, linguistes, ingénieurs… étaient regroupés dans un manoir anglais du nom de Bletchley Park.

Photo du manoir de Bletchley Park. Situé près de Londres, ce manoir de style victorien et des hangars, appelés « huttes », construits dans son parc, abritèrent jusqu’à sept mille personnes décryptant chaque jour les messages ennemis interceptés.
Photo © Matt Crypto / Wikimedia Commons.
Bletchley Park est une propriété située à 80 km environ au nord-ouest de Londres. Idéalement située entre les grands pôles universitaires d’Oxford et de Cambridge, elle a été choisie en 1939 par les services du chiffre britannique pour s’y implanter secrètement. Dans le parc, à côté de la demeure victorienne d’origine, ont été construits plusieurs hangars, baptisés « huttes », où travaillaient les différentes équipes. Alan Turing était affecté à la hutte n° 8, dans une équipe dédiée spécifiquement au décryptage des messages allemands. La traduction en anglais, l’interprétation et la transmission des informations étaient ensuite réalisées dans un autre bâtiment, la hutte n° 4.
Aujourd’hui, Bletchley Park est devenu un musée consacré à la cryptographie et à l’informatique. Il abrite notamment depuis 2007 une réplique du Colossus, un des premiers ordinateurs (construit pour le décryptage), ainsi qu’une imposante statue d’Alan Turing.
Ils utilisèrent le fait que certaines parties des messages étaient faciles à deviner. En particulier, les bulletins météo, transmis chaque matin à la même heure, contenaient tous le mot « Wetter » (qui signifie « temps » en allemand).
Alan Turing eut alors l’idée de rechercher des cycles de lettres. Pour qu’une suite de lettres forme un tel cycle, il faut que chaque lettre de la suite soit une version chiffrée de la lettre précédente, et que la version chiffrée de la dernière lettre corresponde à la première.
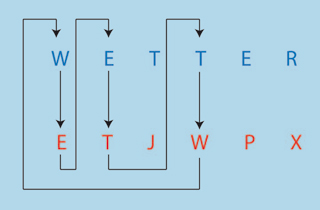
Par exemple, « w », « e » et « t » peuvent former un cycle de trois lettres : « w » est transformé en « e », puis « e » est transformé en « t », finalement « t » est transformé en « w ».
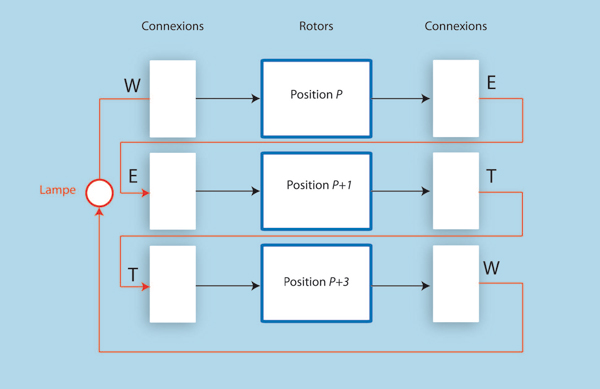
Exemple de cycle de lettres exploité par Alan Turing pour la cryptanalyse d’Enigma.
Comme le tableau de connexions effectue les mêmes transpositions à la fin d’un chiffrement et au début du suivant, son effet s’annule complètement au sein d’un tel cycle. On dispose donc d’un motif caractéristique des rotors : il suffisait alors d’essayer toutes les possibilités pour les rotors pour trouver celle qui produisait le motif attendu. Pour tester le million de possibilités, Alan Turing fit construire des machines électromécaniques appelées « bombes », reproduisant les rotors d’Enigma et permettant d’essayer en parallèle jusqu’à vingt mille configurations par seconde. Une fois la position des rotors déterminée, il devenait possible de décrypter une partie du message (celle correspondant aux six lettres non affectées par le tableau de connexions) puis d’en déduire les transpositions.
Les cryptanalystes de Bletchley Park ne se limitèrent pas à Enigma. Ils attaquèrent également Purple, le système de chiffrement japonais, et la machine de Lorenz, utilisée à partir de 1941 par le commandement suprême des forces armées allemandes. Pour ce faire, ils furent même amenés à construire fin 1943 le premier ordinateur numérique programmable de l’histoire, baptisé Colossus, qui fut, comme toutes les traces de l’activité de Bletchley Park, détruit à la fin de la guerre. Le secret autour de l’opération « Ultra » fut tellement bien gardé pendant trente ans que certains de ces mathématiciens, dont Alan Turing, furent parfois accusés de ne pas avoir contribué à l’effort de guerre.
Depuis la seconde guerre mondiale, le champ d’application de la cryptographie a glissé de plus en plus du domaine militaire vers le domaine économique. Par exemple, la sécurité des données personnelles comme les données médicales est devenue un enjeu crucial.
L’augmentation de puissance des ordinateurs rend naturellement plus rapides les attaques exhaustives sur les systèmes de chiffrement. Les chiffrements actuels doivent donc utiliser des clés de plus grande taille et être plus complexes. Pour mettre à l’épreuve leur sécurité, les chercheurs étudient différents types d’attaques qui exploitent des structures particulières des méthodes de chiffrement, tout comme Alan Turing avait exploité une régularité d’Enigma.
Une avancée majeure, dans les années soixante-dix, a été la définition de la cryptographie à clé publique, à partir du principe mathématique des fonctions à sens unique, faciles à calculer mais en pratique impossibles à inverser. La première réalisation concrète en a été le système RSA, qui repose sur la difficulté de la factorisation de grands nombres entiers. D’autres cryptosystèmes sont construits à partir des courbes elliptiques.
Et demain, peut-être, l’ordinateur quantique viendra-t-il bouleverser ce paysage ?
- Kahn D., Seizing the Enigma, Houghton Mifflin, 1991.
- Singh S., Histoire des codes secrets, J.-C. Lattès, 1999.
- Site internet de Bletchley Park : bletchleypark.org.uk
Cet article est paru dans la revue DocSciences n°14 Alan Turing : La pensée informatique, éditée par le CRDP de l’Académie de Versailles en partenariat avec Inria.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
