Le piano rêvé des mathématiciens
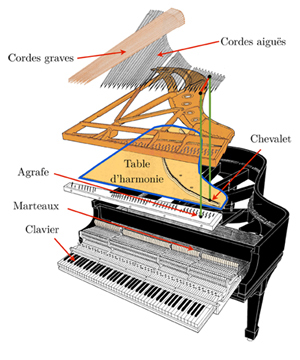
Schéma du mécanisme d’un piano à queue (vue éclatée). D’après l’article d’E.Donnell Blackham. The physics of the piano. Scientific american, 213 (6), 1965.
Le piano est un système acoustique et mécanique assez sophistiqué. On peut résumer très schématiquement son fonctionnement de la façon suivante : le doigt du pianiste frappe une touche du clavier, un mécanisme très précis démultiplie le mouvement de la touche et met en mouvement un marteau. Le marteau frappe entre une et trois cordes à la fois (selon la note choisie), qui se mettent en vibration. Le chevalet permet de transmettre l’énergie des cordes à la table d’harmonie, qui vibre elle aussi, mettant en mouvement les molécules d’air avoisinantes, et entraînant la propagation d’un son dans l’air.
Des équations derrière les touches
Comme la plupart des phénomènes physiques qui nous entourent, le fonctionnement du piano peut être décrit mathématiquement à l’aide d’équations aux dérivées partielles (abrégées en EDP). Les EDP sont des équations qui mettent en relation les dérivées d’une ou plusieurs fonctions par rapport à leurs différentes variables : le temps, l’espace… Certaines EDP sont assez célèbres : l’équation de la chaleur, qui modélise l’évolution de la température dans un milieu ; les équations de propagation d’ondes, qui modélisent la vibration d’une corde et la propagation du son ; les équations de Navier-Stokes, qui interviennent en mécanique des fluides ; les équations de Maxwell, qui sont celles de l’électromagnétisme ; les équations de l’élastodynamique, qui modélisent les ondes sismiques mais aussi la déformation des matériaux ; ou encore l’équation de Schrödinger, qui modélise l’évolution d’une particule quantique.
Revenons à notre piano : chacune des étapes acoustiques citées plus haut peut donc être modélisée par une EDP (pour les cordes, ce sera une équation des ondes monodimensionnelle avec raideur, pour la table d’harmonie, une équation de vibration de plaque, pour l’air, une équation de propagation des ondes tridimensionnelle) ou par une équation d’une autre nature (pour le marteau on aura une équation différentielle ordinaire, au chevalet on exprimera l’égalité des vitesses, et pour le couplage table d’harmonie / air, l’équation traduira l’égalité aussi des vitesses mécanique et acoustique).
De manière générale, les EDP sont des équations complexes dont il est en général impossible de donner la solution au moyen d’une formule. Les problèmes physiques qu’elles traduisent, et qui combinent la plupart du temps plusieurs de ces équations, le sont aussi, à plus forte raison. Diverses méthodes permettent d’en calculer les solutions approchées décrivant le mieux possible la réalité. Cela passe souvent par la discrétisation du problème et par le calcul sur ordinateur de solutions approchées.
Quand on s’intéresse à des applications concrètes des EDP (en météorologie, en sismologie, en aéronautique, en construction automobile…), il ne suffit pas de connaître l’existence et le comportement d’une solution dans son espace abstrait mathématique. Les physiciens ont besoin de pouvoir au moins estimer cette solution quantitativement.
La science qui consiste à chercher une approximation de la solution d’une EDP de façon précise et performante grâce à l’utilisation d’ordinateurs est celle du calcul scientifique et de l’analyse numérique. L’idée est de ramener l’infini de l’espace mathématique de la solution de l’EDP au caractère foncièrement fini et discret (par opposition à continu) de l’ordinateur, mais en s’assurant que plus on fera d’efforts (en termes de temps de calcul ou de puissance du processeur), plus on s’approchera de la « vraie » solution. Une des méthodes les plus connues et les plus répandues dans l’industrie est probablement la méthode des éléments finis.
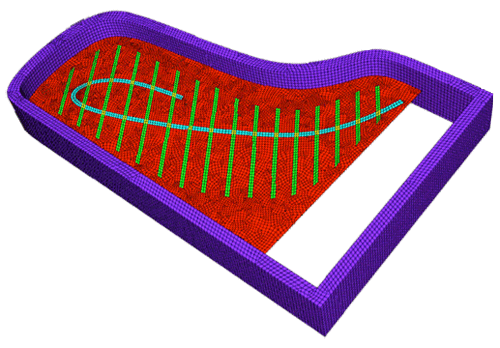
Maillage d’une table d’harmonie. © Juliette Chabassier 2012
C’est ce que l’on fait dans le cas du piano : un modèle général est établi grâce aux équations, puis discrétisé sous la forme d’un maillage (voir ci-dessus), et enfin les solutions sont calculées numériquement grâce à des méthodes d’analyse numérique développées précisément pour l’occasion.
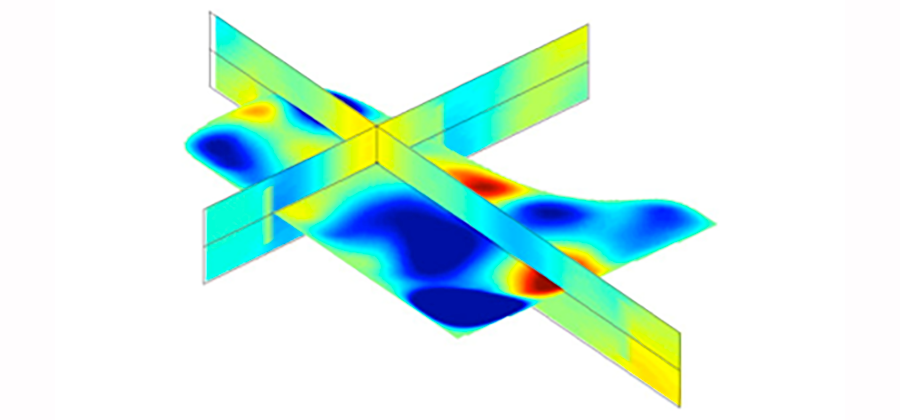
Visualisation des vibrations de corde, table d’harmonie et rayonnement du son dans l’air après sollicitation de la note D♯1 (Ré dièse 0 en notation française).
© Juliette Chabassier 2012 – Durée : 00 min 30 s (film muet).
Grâce à ce modèle et aux simulations numériques qui en découlent, on parvient à reproduire fidèlement des formes d’ondes, mais aussi, par exemple, à connaître le champ de pression de l’air sur un ensemble de points tout autour du piano, ce qui serait impossible à mesurer sans perturber le système : si on essayait de faire cette mesure en entourant le piano d’un réseau de capteurs, la présence même de ce réseau provoquerait un phénomène de diffraction du son et fausserait donc la mesure effectuée.
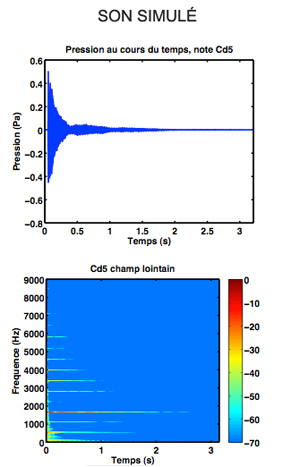
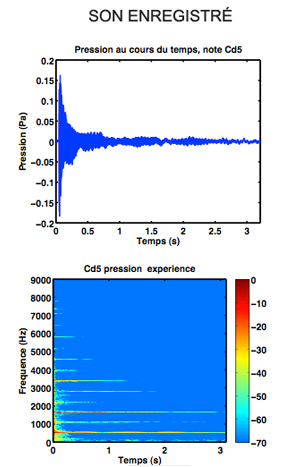
© Juliette Chabassier 2012
Pour écouter le rendu, voici un fichier sonore réalisé uniquement à partir de sons calculés par notre modèle de piano.
Illustration sonore : J. Pachelbel : Chaconne en Fa mineur (interprète : Noa Leigh Kleisen, e-competition 2008)
© Juliette Chabassier 2014
Étant donnée la complexité des phénomènes physiques pris en compte, le calcul n’est pas fait en temps réel. En effet, il faut environ 24h pour calculer, sur 300 processeurs, une seconde de vibrations dans tout le piano et l’air… Nous avons donc précalculé toutes les notes à différentes nuances de jeu (du pianissimo au fortissimo) ce qui nous a permis de générer une « banque de sons » grâce au logiciel Polyphontics. Un fichier midi, qui contient l’interprétation d’un pianiste, peut ensuite être écouté grâce à cette banque. Le rendu est très réaliste, on reconnaît tout à fait le son d’un piano et les différentes couleurs obtenues en faisant varier la nuance. Quelquefois les notes s’arrêtent un peu brutalement, ceci est dû au fait que nous n’avons pas (encore) modélisé les étouffoirs (pièces de feutres qui étouffent le son).
Pianos virtuels
L’une des applications les plus enthousiasmantes de ce modèle et de sa discrétisation numérique est l’aide à la facture instrumentale. Aujourd’hui, la facture du piano est majoritairement basée sur un savoir empirique issu de siècles d’expérimentations, d’échecs, de succès… Les facteurs, c’est-à-dire ceux qui conçoivent et réalisent les instruments, ont ainsi acquis un ensemble de connaissances extrêmement précises. On trouve par exemple dans la littérature spécialisée des affirmations telles que : « les rouleaux des marteaux influent sur le toucher du piano à queue de façon décisive », ou encore « la table d’harmonie est en épicéa de Sitka, un bois d’une densité et d’une élasticité idéales pour la résonance ». Ces affirmations intriguent beaucoup les chercheurs en acoustique musicale qui s’attachent, en utilisant des méthodes scientifiques, à leur donner raison ou tort, et à aller plus loin dans la compréhension des phénomènes mis en jeu. Le modèle de piano peut alors permettre d’isoler certains phénomènes afin de comprendre leur influence sur le son, sur le rayonnement, ou encore sur la transmission de l’énergie… mais aussi de construire virtuellement des pianos qui n’existent pas (changer la forme ou la taille de la table, les matériaux utilisés, la façon de l’utiliser, etc) et de pouvoir écouter le son qu’ils auraient s’ils étaient construits.
Une question controversée est celle de l’influence du toucher pianistique sur le son. Il ne fait aucun doute que le pianiste a une grande emprise sur le son de l’instrument, à travers un ensemble de paramètres qu’il maîtrise et contrôle grâce à sa technique de jeu : nuance, articulation, subtiles variations de tempo, utilisation des pédales… et toucher. On définit le toucher comme la façon dont le doigt sollicite la touche, toutes choses égales par ailleurs. Sur une note isolée, des chercheurs ont essayé de mesurer l’impact de ce paramètre sur le son, aboutissant à des conclusions contradictoires. Il semblerait cependant que la vibration du manche de marteau joue un rôle prépondérant.

Une mécanique de piano à queue. © Jorge Royan / ![]() Cette œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution 4.0 International.
Cette œuvre est mise à disposition selon les termes de la Licence Creative Commons Attribution 4.0 International.
Grâce à notre outil numérique, nous avons pu modéliser cette vibration et l’intégrer au modèle complet de l’instrument. Les vidéos ci-dessous montrent la déformation du manche et de la tête du marteau pour deux touchers « caractéristiques » : staccato (une impulsion de force courte et puissante) et legato (une montée lente de la force exercée). La tête de marteau frappe ensuite les cordes avec une vitesse identique, ce qui signifie que la même quantité d’énergie est délivrée aux cordes dans les deux cas, mais avec une répartition différente au cours du temps. Ensuite, l’énergie se propage virtuellement dans l’instrument et rayonne dans l’air : le son résultant peut être analysé. On observe que, selon le toucher mis en œuvre, l’énergie se répartit différemment entre les harmoniques, en particulier entre le 14e et le 19e harmonique. L’influence du toucher pianistique sur le son est donc démontrée par cette expérience numérique. Elle met de plus en évidence un mouvement horizontal de la tête du marteau, qui pour l’instant n’est pas prise en compte dans les modèles classiques mais semble elle aussi avoir une influence sur le son.
Visualisation des vibrations du manche de marteau de piano et de la compression de la tête de marteau (amplifiés en bleu) pour un toucher staccato sur la note D♯1 (Ré dièse 0 en notation française).
© Juliette Chabassier 2014 – Durée : 00 min 08 s (film muet).
Visualisation des vibrations du manche de marteau de piano et de la compression de la tête de marteau (amplifiés en bleu) pour un toucher legato sur la note D♯1 (Ré dièse 0 en notation française).
© Juliette Chabassier 2014 – Durée : 00 min 15 s (film muet).
Encore plus intrigant, le modèle permet de générer des sons d’objets qui ne peuvent pas exister pour des raisons pratiques (matériaux inventés, cordes de sept mètres de long, piano flottant sans cadre ni pieds…) mais qui pourtant respectent les lois de la physique et dont le son paraît donc plausible à l’oreille (en ce sens que le cerveau parvient à les attribuer à un événement, une cause physique, une dynamique associée). On touche là une application très intéressante du point de vue de l’interaction entre science et musique : la recherche offre au compositeur des instruments nouveaux, un matériau sonore jusqu’ici inexistant et adaptable à souhait. À une époque où le timbre et la manipulation du son sont au cœur de la création musicale, la modélisation instrumentale ouvre au musicien des champs d’exploration inouïs.
Ces possibilités sont parfaitement illustrées par les travaux du compositeur Guillaume Loizillon, qui utilise Modalys, un logiciel de synthèse sonore par modèles physiques développé à l’Institut de Recherche et Coordination Acoustique/Musique (IRCAM) et permettant de modéliser une multitude d’instruments existants ou chimériques. Il dit à ce sujet : « Ce que je trouve intéressant dans Modalys, plus que l’imitation d’un timbre, c’est que cela permet, au niveau d’un son unique, de donner, de manière assez évidente, l’idée de la matière, du métal, du bois. Deuxième chose, cela permet de créer des dynamiques, des événements et non pas des objets. […] C’est-à-dire que le son raconte un événement : cela roule, cela rebondit. »
Le compositeur peut même dépasser le monde physique existant et en imaginer un autre, aux lois différentes : « Ensuite ce que j’aime c’est aller dans des modèles plus utopiques » poursuit Guillaume Loizillon. « Avec Jean-Claude Risset [NDLR : compositeur également], on avait discuté du sujet est-ce que l’on peut créer une physique non terrienne. […] On peut imaginer une physique où les objets rebondissent pendant des heures et des heures, où la pesanteur n’est plus la même. »
Les citations de Guillaume Loizillon sont extraites de La synthèse par modèles physiques, mémoire de maîtrise de Aline Hufschmitt, Université Paris Sorbonne (Paris IV).
- Site web : http://modelisation.piano.free.fr
- Juliette Chabassier, Antoine Chaigne, and Patrick Joly. Modeling and simulation of a grand piano. Acoustical Society of America, 2013.
Crédits calculs : Toutes les simulations ont été réalisées en utilisant les moyens de calcul du GENCI : TITANE – CEA / CCRT et JADE – CINES, la plate-forme expérimentale PLAFRIM, développée par Inria PlaFRIM avec le support du LABRI, de l’IMB et d’autres entités : conseil régional d’Aquitaine, FeDER, université de Bordeaux et CNRS, et les moyens de calcul du MCIA (Mésocentre de calcul intensif aquitain) de l’université de Bordeaux et de l’université de Pau et des Pays de l’Adour.
Une première version de ce document est parue dans la brochure Mathématiques, L’explosion continue réalisée par la Fondation Sciences Mathématiques de Paris (FSMP), la Société Française de Statistiques (SFdS), la Société de Mathématiques Appliquées et Industrielles (SMAI) et la Société Mathématique de France (SMF).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Antoine Chaigne
Responsable de l'unité d'enseignement et de recherche en mécanique ENSTA-UME.

Marc Duruflé