
Les limites de la croissance dans un monde fini
(Par essence, tous les modèles sont faux, mais certains sont utiles.)
George Box (1919-2013)
dans Empirical Model Building and Response Surfaces
Box, G. E. P., and Draper, N. R., John Wiley & Sons, New York, NY, 1987
La croissance peut-elle se poursuivre dans un monde fini ? Il y a quarante ans, un modèle mathématique global de l’activité humaine apportait des réponses à cette question critique.
En 1972 paraissait l’ouvrage de Donella Meadows, Dennis Meadows, Jørgen Randers et William W. Behrens, The Limits to Growth, dont le titre neutre fut malencontreusement transformé en Halte à la croissance ? dans l’édition française de la même année [1]. Il s’agissait du rapport de synthèse d’une étude commanditée par le Club de Rome, une association informelle de personnalités de l’industrie, de l’économie et de la science, à une équipe du Massachusetts Institute of Technology (MIT) spécialisée dans la modélisation et la simulation de systèmes socio-économiques.
L’avenir mondial selon World3
Ce rapport examinait plusieurs scénarios à long terme pour la planète. Pour ce faire, l’équipe dirigée par Dennis L. Meadows avait élaboré une version étendue du modèle World2, initialement conçu par Jay W. Forrester pour convaincre le Club de Rome de l’intérêt de la démarche. Cette version étendue, baptisée logiquement World3, reliait entre elles, à travers un ensemble d’équations différentielles, un petit ensemble de variables, telles que la population, le niveau des ressources non renouvelables, la surface des terres cultivables, la production industrielle, etc., toutes agrégées au niveau mondial. De cinq dans le modèle World2 de Jay Forrester [2], ces variables passaient à une quinzaine dans la version World3 décrite par le groupe de Dennis Meadows [3].
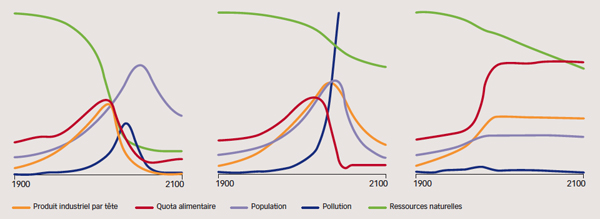
Trois scénarios issus du rapport Meadows. À gauche, scénario dans lequel les tendances des années 1900-1970 se poursuivent. Au centre, scénario intégrant une optimisation de l’utilisation des ressources non renouvelables. À droite, scénario faisant intervenir des politiques conjointes de stabilisation.
© Vincent Landrin (d’après The Limits to Growth, 1972).
Ce modèle, à travers sa simulation sur ordinateur, permettait d’étudier divers scénarios d’évolution des variables, de 1900 à 2100 (voir schémas ci-dessus). Le scénario de base (à gauche) explorait ainsi les conséquences d’une poursuite des activités humaines dans le prolongement de la croissance exponentielle des années 1900 -1970. Il mettait en évidence un ralentissement de la croissance, suivi, aux alentours de 2020, d’un déclin, y compris de la population humaine. Étaient alors étudiées diverses actions destinées à éviter cette évolution jugée néfaste. Toutes menaient, au mieux, à repousser ce déclin de quelques années, au pire, à des situations plus catastrophiques encore. Par exemple, une meilleure utilisation des ressources naturelles non renouvelables conduisait à une hausse spectaculaire de la pollution, c’est-à-dire une dégradation de l’environnement, qui avait un impact dramatique sur la population (au centre). Seule une série d’actions conjointes sur les différentes variables permettaient d’arriver à stabiliser le système sans passer par des épisodes dramatiques (à droite).
Le rapport a été l’objet de vives critiques, à la fois sur les conclusions (il recommandait de chercher à atteindre un état d’équilibre dynamique, où l’activité se poursuit, mais où toutes les variables sont stabilisées, les flux entrants contrebalançant les flux sortants), et sur la méthode (est-il raisonnable de prédire l’évolution du système mondial sur une période s’étendant sur deux cents ans à l’aide d’un modèle extrêmement agrégé reposant sur des données d’une pertinence toujours discutable ?).
Néanmoins, certains s’accordaient à penser que ce rapport avait le mérite de promouvoir une vision globale des problèmes liés à la croissance des activités humaines. Il illustrait un message simple et fort : la croissance exponentielle ne peut se poursuivre dans un monde fini. Il montrait comment cette croissance rencontrait des limites multiples sans s’y heurter brutalement, mais avec des conséquences dramatiques sur le long terme. Ce rapport mettait également en avant la nécessité de disposer d’outils capables d’aborder la complexité des systèmes socio-économiques. L’évolution de ces systèmes résulte à l’évidence de très nombreuses interactions formant des boucles dont le comportement échappe très vite aux prospectivistes en l’absence de modèles mathématiques simulables.
Des équations et de nombreuses inconnues
Revenons donc sur ces modèles mathématiques qui furent tant décriés. Formellement, il s’agit de systèmes d’équations différentielles ordinaires non linéaires, qui font intervenir différentes variables d’état, telles que la population, la surface de terres cultivables ou encore les ressources naturelles non renouvelables. Chacune des équations explicite la relation entre le taux de variation instantanée, autrement dit la dérivée, d’une variable d’état, et les autres variables du modèle. Ainsi, l’équation décrivant, dans le modèle World2, l’effectif de la population mondiale fait intervenir le nombre de naissances et le nombre de décès comptés en naissances et décès pour mille et par an. Chacune de ces deux variables est à son tour reliée par une chaîne d’équations algébriques à plusieurs autres variables d’état, dont le niveau de pollution. Ces équations sont non linéaires : les variations de ces variables ne sont pas obligatoirement proportionnelles entre elles.
L’élaboration d’un modèle est un processus délicat. Il faut identifier les variables pertinentes, formuler les équations qui les relient et fixer les valeurs des paramètres qui y apparaissent. Les auteurs de World2 et World3 disposaient-ils de toutes les informations et données requises ? Très certainement non. Quelle est alors la valeur de ces modèles ?
Un modèle doit être vu comme un rassemblement raisonné d’hypothèses. Hors des domaines où il peut s’appuyer sur de véritables lois, le modélisateur est conduit à faire des choix sur la base de ce qu’il connaît du système et surtout des questions qui motivent la construction du modèle. Chaque équation exprime de fait une ou plusieurs hypothèses sur la relation entre les variables qu’elle relie. Dans ce contexte, l’intérêt de la formulation mathématique réside dans la possibilité de calculer les conséquences de cet ensemble d’hypothèses à travers la simulation du modèle.
C’est quand les comportements simulés ne sont pas ceux attendus que le modélisateur est susceptible d’apprendre le plus : des relations manquent-elles ? Des variables importantes ont-elles été écartées indûment ? Des formulations d’équations sont-elles erronées par rapport aux hypothèses retenues ? À travers ce processus itératif, qui alterne simulations et révisions du modèle, la compréhension du système et de sa dynamique s’accroît.
Les chercheurs du MIT ont publié l’intégralité des équations des modèles World2 et World3, se livrant ainsi aux critiques (qui n’ont pas manqué [4]) et permettant à tout un chacun, non seulement de reproduire les résultats publiés, mais aussi de modifier la formulation mathématique pour intégrer d’autres hypothèses et en tirer des comportements nouveaux.
Pertinence et limites des modèles
Au-delà de l’impact de ces études sur les limites de la croissance, World2 et World3 constituent une excellente étude de cas sur ce qu’il convient de qualifier de bon modèle.
Un bon modèle est-il un modèle qui « colle » à la réalité, comme l’ont à l’époque brutalement répété les économétriciens [5] ? Que vaut cependant un modèle qui reproduit une réalité passée, mais qui est impuissant, par sa conception même, à produire des scénarios de crise, tout simplement parce que les interactions qui s’activent alors au sein du système ne se sont jamais produites auparavant et n’ont donc pu faire l’objet de mesures ?
Un bon modèle est-il un modèle complet ? Un modèle complet d’un système serait de même complexité que son objet, aussi inutile, et inenvisageable, qu’une carte à l’échelle 1:1. Tout modèle est donc incomplet et faux par essence.
Un bon modèle est un modèle utile, qui répond aux questions ayant motivé sa conception, un modèle qui contribue à mieux comprendre le système étudié et qui permet de tester des hypothèses et de confronter des alternatives.
World2 et World3 ont-ils été utiles ? À leurs concepteurs, sans nul doute. À tous ceux qui les ont étudiés, critiqués, reproduits et simulés pour tester des hypothèses et des scénarios alternatifs, très certainement. Au-delà, on laissera au lecteur le soin de déterminer à quel point ces modèles ont eu un impact sur le débat sur la croissance, d’abord à l’époque de sa parution, et surtout quelques mois plus tard, quand le problème de la croissance s’est trouvé posé en des termes radicalement différents. En effet, dès le milieu des années 1970, face à une crise énergétique et économique sans précédent, les interrogations sur les limites de la croissante se sont rapidement effacées au profit d’une recherche des moyens de la relancer…
- The Limits to Growth, Donella Meadows, Dennis Meadows, Jørgen Randers et William W. Behrens, New York, Universe Books, 1972 ; traduction française Halte à la croissance ? Rapport sur les limites de la croissance, précédé de : Enquête sur le Club de Rome, Janine Delaunay, Paris, Fayard, 1972
- World Dynamics, Jay W. Forrester, Wright-Allen Press, 1971
- Dynamics of Growth in a Finite World, Dennis L. Meadows, William W. Behrens III, Donella H. Meadows, Roger F. Naill, Jørgen Randers, et Erich K.O. Zahn, Wright-Allen Press 1974
- Models of Doom: A Critique of the Limits to Growth, Marie Jahoda, K. L. R. Pavitt, H. S. D. Cole, et Christopher Freeman, Universe Publishing, 1973
- « World Dynamics: Measurement Without Data », William D. Nordhaus, The Economic Journal, Vol. 83, No. 332. (Déc., 1973), pp. 1156-1183
- Les limites à la croissance (dans un monde fini) : le rapport Meadows, 30 ans après, Donella Meadows, Dennis Meadows, Jørgen Randers, traduction française par Agnès El Kaïm, Paris, Rue de l’Échiquier, 2012
[2] World Dynamics, Jay W. Forrester, Wright-Allen Press, 1971
[3] Dynamics of Growth in a Finite World, Dennis L. Meadows, William W. Behrens III, Donella H. Meadows, Roger F. Naill, Jørgen Randers, et Erich K.O. Zahn, Wright-Allen Press 1974
[4] Models of Doom: A Critique of the Limits to Growth, Marie Jahoda, K. L. R. Pavitt, H. S. D. Cole, et Christopher Freeman, Universe Publishing, 1973
[5] « World Dynamics: Measurement Without Data », William D. Nordhaus, The Economic Journal, Vol. 83, No. 332. (Déc., 1973), pp. 1156-1183
Une première version de cet article est parue sous le titre La croissance en question dans la revue Textes et documents pour la classe (TDC) n° 1062 « Les mathématiques de la Terre », éditée par le CNDP, en partenariat avec Inria et à l’initiative du comité éditorial d’Interstices.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
