Modélisation en dynamique des populations
La modélisation des dynamiques des populations vise à expliquer, et éventuellement à prévoir, les évolutions d’une population dans un cadre écologique ou géographique donné. La plupart du temps, elle se limite à la description des variations de la taille de la population, mais elle peut aussi permettre de décrire l’évolution de sa structure en âge ou en biomasse, voire de sa structure génétique. Les scientifiques ont, dès le XIIIe siècle, proposé des « modèles », c’est-à-dire des représentations simplifiées de telles dynamiques, le plus souvent sous forme mathématique.
Cette démarche, qui s’est à l’origine concentrée sur la dynamique des populations humaines, également appelée démographie, s’applique aussi à la dynamique de ressources végétales (telles que les forêts) ou animales (comme les espèces d’intérêt halieutique) et est généralement couplée à des outils de gestion visant à optimiser l’exploitation durable de ces ressources naturelles. Ces modèles peuvent également rendre compte de dynamiques d’écosystèmes. L’un des modèles les plus emblématiques, proposé au début du XXe siècle par Alfred Lotka et Vito Volterra, permet par exemple d’expliquer les cycles continuels des effectifs des populations de proies et de prédateurs en interaction, selon l’enchaînement logique suivant : en consommant les proies, les prédateurs se multiplient et les proies se raréfient, ce qui provoque alors la disparition des prédateurs, induisant de nouveau la multiplication des proies, et ainsi de suite.
Pour une introduction à la dynamique des populations, voir Des espèces en nombre.
Du déterminisme au probabilisme
Bien que les phénomènes de démographie, de compétition pour l’accès aux ressources ou bien encore de prédation soient clairement aléatoires, l’une des préoccupations majeures de la discipline a tout d’abord consisté à dégager des « déterminismes », c’est-à-dire des tendances reproductibles malgré tous ces aléas. Cette démarche est applicable aux populations de grande taille, lorsque ces différentes sources d’incertitude se compensent et que les variables peuvent être représentées de façon continue à l’aide de nombres réels.
Dans cette optique, la modélisation des dynamiques des populations s’est initialement développée à l’aide d’équations différentielles déterministes. Ces équations fournissent une relation entre une quantité inconnue, ici la taille d’une population, et sa dérivée en temps. L’analyse théorique de ces équations est souvent possible
et fournit des informations pertinentes. On peut également développer des outils informatiques qui permettent de simuler sur ordinateur une approximation d’une trajectoire de cette équation, c’est-à-dire l’évolution de l’effectif de la population à partir d’une taille de population initiale fixée.
Cette quête du déterminisme faisait suite aux succès de la modélisation mathématique en mécanique newtonienne. Il était en effet tentant de dégager en biologie des lois universelles déterministes équivalentes à celles de la mécanique.
Cette démarche a largement occulté la prise en compte des phénomènes aléatoires pourtant essentiels en biologie et en écologie. Les travaux tentant de rendre compte de cet aléa faisaient face à deux difficultés : leur analyse mathématique est moins aisée et les outils de simulation ne se sont développés que tardivement. Cette approche s’est donc à l’origine limitée à certains domaines de la génétique où l’aléa est intrinsèquement incontournable.
Ainsi, les efforts de modélisation se sont portés non pas sur des approches probabilistes, bien que certains scientifiques aient pu reconnaître qu’elles étaient pertinentes, mais sur celles produisant rapidement des résultats. Ce biais, souvent rencontré en recherche, est parfois appelé « effet lampadaire », en référence à une
plaisanterie bien connue des scientifiques : la nuit, une personne recherche ses clefs sous un lampadaire, non parce qu’elle les a perdues à cet endroit, mais parce que c’est le seul qui soit éclairé !
Les modèles à l’ère numérique
Il a fallu attendre le développement des premiers ordinateurs, mais surtout leur démocratisation à la fin des années 1970, pour que la simulation numérique vienne concurrencer ou du moins compléter l’analyse mathématique. C’est à cette époque que seront popularisés les premiers algorithmes de simulation, dits « de Monte-Carlo », de systèmes dynamiques stochastiques, c’est-à-dire portant sur des quantités évoluant au cours du temps et dépendant du hasard.
Contrairement aux modèles précédents où les tailles de populations sont décrites par des variables continues (des réels), ces systèmes peuvent être exprimés à l’aide de variables discrètes (des entiers). Ils permettent ainsi de rendre compte de phénomènes intéressants, notamment pour les populations de petite taille.
Par exemple, les modèles classiques déterministes en variables continues peuvent présenter des artefacts de simulation, comme celui dit de « l’atto-fox » mis en évidence dans un modèle de diffusion de la rage décrit en variables continues. Ce modèle prédisait une recrudescence de la population de renards, alors que celle-ci était descendue en deçà de 10-18 individus au mètre carré !
Les approches alternatives aléatoires en variables discrètes permettent une interprétation plus appropriée, notamment en termes de probabilité d’extinction. En revanche, ces approches n’ont que peu d’intérêt lorsque les méthodes classiques, beaucoup plus simples à simuler, sont valides.
Vers la fin d’un antagonisme
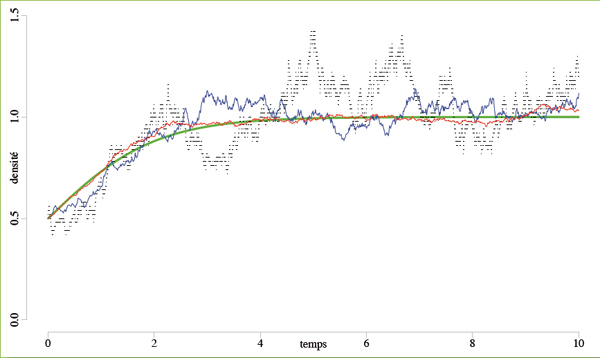
Des formalismes adaptés à chaque situation.
Le graphique ci-dessus simule les trajectoires d’évolution de la densité de populations au cours du temps pour un modèle de croissance logistique, c’est-à-dire dans le cas d’un modèle de croissance exponentielle graduellement ralentie par saturation de l’environnement. Pour les populations de petite taille, la simulation discrète/stochastique (en noir) est préférable : elle converge vers la solution de l’équation différentielle classique (en vert). Pour les populations de taille moyenne (en bleu) ou de grande taille (en rouge), on obtient un comportement presque continu.
© Fabien Campillo / Inria
Les approches continue/déterministe et discrète/aléatoire se développent souvent en opposition et le choix entre les deux est moins guidé par la pertinence pour l’application que par la culture du modélisateur. Toutefois, une nouvelle voie émerge : elle consiste à ce qu’un même modèle puisse être exprimé à la fois de façon
continue/déterministe et discrète/aléatoire. Selon les domaines dans lesquels on souhaite explorer ce modèle, on se tournera vers l’un ou l’autre des formalismes.
Elle propose également des approches hybrides, où des modèles continus pour les populations de grande taille sont couplés à des modèles discrets pour les populations de petite taille. En effet, il serait pertinent de contrôler la dynamique lorsqu’elle s’approche de tailles de populations faibles et d’en avertir l’utilisateur en lui proposant de passer à des techniques de simulation discrètes. On envisage donc le passage automatique d’un mode de simulation à l’autre lorsque la taille de la population fluctue.
Ainsi, les principaux outils de modélisation semblent actuellement établis. Des efforts en revanche restent à faire en matière de formation comme d’intégration algorithmique et logicielle pour enfin réconcilier les formalismes continu/déterministe et discret/aléatoire que tout semblait opposer.
- BACAËR Nicolas. Histoires de mathématiques et de populations. Paris : Cassini, 2009.
- CHARLES Sandrine, CHARLES Hubert. Des espèces en nombre.
- Processus stochastiques en temps continu pour la modélisation en écologie. Cours de master de biostatistique de Fabien Campillo et Marc Joannides, en ligne.
Cet article est paru dans la revue Textes et documents pour la classe (TDC) n° 1062 « Les mathématiques de la Terre », éditée par le CNDP, en partenariat avec Inria et à l’initiative du comité éditorial d’Interstices.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
