L’art de couper les têtes sans faire mal
Il paraît difficile de « couper » une tête pour en voir l’intérieur sans faire mal à son propriétaire. C’est pourtant ce que les équipes médicales peuvent réaliser à l’aide des scanners, ou tomodensitomètres en français. Cet outil de diagnostic des dommages internes est disponible depuis les travaux de Godfrey Hounsfield et Allan McLeod Cormack, deux physiciens qui ont partagé le prix Nobel en 1979 pour cette invention. Le scanner n’aurait pu exister sans le mariage de la physique, des mathématiques et de l’informatique.
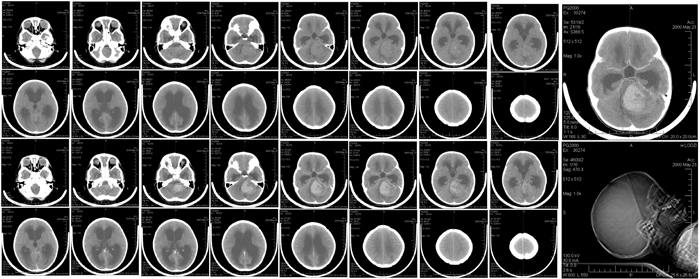
Tomodensitométrie du cerveau d’un enfant. Image : Reytan via Wikimedia Commons.
Problème direct, problème inverse
À l’inverse de la radiographie classique à rayons X, l’image d’un scanner n’est pas obtenue directement par une mesure physique mais est créée par un ordinateur à l’aide d’algorithmes mathématiques à partir d’une collection de radiographies de la tête du patient prise sous des angles différents. Pour réaliser une telle prouesse, il faut savoir résoudre deux problèmes : comprendre comment cette collection de radiographies dépend de l’intérieur de la tête du patient, on parle de problème direct, et comprendre comment remonter de la collection de radiographies à ce qui se passe à l’intérieur de la tête, on parle alors de problème inverse.
Le problème direct est ici le même que celui de la radiographie à rayons X. Son principe a été découvert par Wilhelm Conrad Roentgen en 1895 et a immédiatement été utilisé pour diagnostiquer des blessures internes. Il a été largement étudié d’un point de vue physique : on sait ainsi que la radiographie obtenue dépend essentiellement de la quantité de matière absorbante rencontrée par le rayonnement X entre la source et le capteur. C’est pour cela que les os, plus absorbants que les tissus, sont les structures naturelles les plus visibles. En prenant en compte les caractéristiques physiques des instruments de radiographie utilisés, on sait alors prévoir mathématiquement de manière très fine la radiographie d’un objet supposé entièrement connu. Il en est donc de même pour la collection de radiographies obtenue par le scanner.
Bien que très précise, cette modélisation n’est pas parfaite : la radiographie mesurée sera légèrement différente de la radiographie prédite du fait de simplifications physiques, de l’imprécision des différents capteurs et d’autres aléas.
Retrouver l’objet à partir des radiographies
Retrouver l’objet à partir de la collection de radiographies, le problème inverse, s’avère être un problème beaucoup plus difficile. Il faut réussir à inverser la procédure d’acquisition du scanner par un principe implémentable dans un ordinateur. De plus, il faut que de petites imprécisions sur le modèle n’induisent pas de grandes erreurs sur le résultat. C’est la mise en œuvre d’une solution à ce problème qui a permis l’existence de la première génération de scanners à la fin des années 60. Depuis lors, les évolutions technologiques des sources de rayons X, des capteurs ainsi que des autres mécanismes instrumentaux ont permis une amélioration de la qualité des images obtenues. Elle requiert beaucoup moins de vues que les 180 vues de la première génération de scanner, et surtout une beaucoup plus petite dose de rayons X. Cette amélioration aurait été bien moindre sans le travail des mathématiciens et le développement de nouveaux algorithmes d’inversion.
Un principe simple, souvent appelé principe du rasoir d’Ockham, est à la source de la plupart des méthodes modernes pour résoudre ce problème. Guillaume d’Ockham, un moine philosophe franciscain du XIVe siècle, expliquait que « les multiples ne doivent pas être utilisés sans nécessité ». Dans son incarnation moderne, le rasoir d’Ockham est un principe de parcimonie : une bonne solution est une solution compatible avec les données observées tout en n’étant pas inutilement complexe.
Pour appliquer ce principe de bon sens, il faut bien sûr donner une définition précise (et mathématique) de la « compatibilité » et de la « complexité », ainsi que proposer une manière d’obtenir une solution à la fois compatible et peu complexe.
Aucune des méthodes de résolution du problème inverse ne faisant l’unanimité, les mathématiciens, ainsi que les fabricants de scanners, continuent d’explorer les possibilités. L’une d’entre elles, sur laquelle a travaillé l’auteur de cet article, est illustrée par la figure ci-dessous.

Méthode de résolution du problème inverse.
Complètement à gauche se trouve une image test appelée fantôme de Logan-Shepp, souvent utilisée pour évaluer les méthodes ; l’image immédiatement à sa droite correspond aux mesures d’un scanner parfait (cette image bidimensionnelle est obtenue en juxtaposant les « tranches » correspondant à différents plans de coupe). L’image suivante correspond à des mesures légèrement perturbées. On parle souvent de bruit pour la différence entre les mesures idéales et les mesures légèrement perturbées. Enfin, on a représenté au dessous trois équilibres différents entre l’incompatibilité (l’image de la colonne de gauche est d’autant plus blanche que l’incompatibilité avec les mesures est grande) et la complexité (l’image de la colonne de droite correspond à des solutions de complexité croissante du haut vers le bas). Une solution pas assez complexe conduit à une incompatibilité forte, tandis qu’une solution trop incompatible donne une solution trop complexe pour correspondre à la réalité (l’effet du bruit y est très prononcé).
© Erwan Le Pennec.
On observe que la meilleure solution semble bien être celle qui réalise le meilleur compromis entre compatibilité et complexité.
IRM, imagerie sismique et autres problèmes similaires
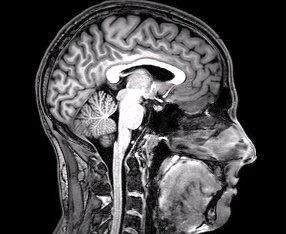
IRM fonctionnelle. Image : DrOONeil via Wikimedia Commons (CC BY-SA).
De nombreux problèmes similaires existent en imagerie, on peut citer par exemple :
- l’IRM (Imagerie en Résonance Magnétique), où l’on cherche à déterminer les structures à l’intérieur d’un corps en mesurant leurs influences sur des champs magnétiques,
- la déconvolution optique, où l’on cherche à enlever le flou dû à la lentille dans une photographie,
- l’imagerie sismique, où l’on cherche à déterminer les structures souterraines à partir d’enregistrements de propagations d’ondes.
Dans chacun d’eux, on retrouve un problème direct, l’étude de la formation des mesures à partir d’un objet, et un problème inverse, dans lequel on cherche à revenir des mesures à l’objet. Dans le cas de l’IRM, on sait établir la réponse électromagnétique d’un objet à un champ magnétique et on cherche à retrouver l’objet à partir de mesures de cette réponse. Dans le cas de la déconvolution, on sait comment l’image idéale est déformée par la lentille avant d’arriver aux capteurs et on cherche à retrouver cette image idéale à partir de l’image enregistrée. Une des applications les plus connues est la correction du défaut de la lentille du télescope spatial Hubble en 1990. Enfin, dans le cadre de l’imagerie sismique, on connaît la trajectoire des ondes sismiques en fonction de la composition du sol et on souhaite retrouver cette composition à partir de l’enregistrement de temps de trajets d’ondes sismiques à travers celui-ci.
Pour chacun de ces exemples, le principe du rasoir d’Ockham a prouvé son efficacité pour obtenir des résultats théoriques et pratiques. Les questions autour de ces problèmes inverses sont cependant loin d’être closes : de nouveaux dispositifs d’acquisition sont régulièrement introduits, de nouveaux moyens de calcul toujours plus puissants permettent d’envisager des méthodes de plus en plus complexes, de nouveaux outils mathématiques permettent également d’explorer de nouvelles voies…
La modélisation la plus commune du problème évoqué dans cet article est l’observation d’un objet O à travers sa collection de radiographies R obtenue par l’application d’une fonction Φ venant du modèle direct auquel est ajoutée une perturbation B inconnue. On observe ainsi
R = Φ (O) + B
et l’on souhaite retrouver au mieux O à partir de la collection de radiographies R.
Une idée naturelle pour un mathématicien est de déterminer l’inverse Φ-1 de la fonction Φ et de l’appliquer à R pour retrouver O. Malheureusement, on vérifie que l’objet ainsi obtenu
Φ-1(R) = Φ-1(Φ(O)+B))
peut être très différent de O même si B est petit. On dit que l’inversion est instable.
Pour appliquer le principe d’Ockham, il faut définir le critère de compatibilité ainsi que de complexité.
Le mathématicien définit ainsi une fonction d’incompatibilité F (R,O) qui quantifie la différence entre la radiographie observée R et celle prévue par le modèle direct pour un objet O : cette fonction est petite lorsque l’objet O est compatible avec les observations et grande lorsqu’il est incompatible.
De même, il définit une mesure de complexité C (O) grande quand l’objet est complexe et petite quand l’objet est simple.
Il peut alors interpréter le principe d’Ockham comme la recherche d’un objet O réalisant le meilleur compromis entre ces deux quantités, un objet pour lequel la somme
F (R,O) + C (O)
est la plus petite possible.
Les expériences numériques de la figure ont été obtenues en choisissant pour critère de compatibilité essentiellement la distance usuelle entre l’image de l’objet Φ(O) et R, et pour critère de complexité, la parcimonie, le nombre de coordonnées non nulles, dans une représentation adaptée, une base de needlets. Ce choix permet d’obtenir des garanties théoriques sur la reconstruction ainsi qu’un algorithme efficace de détermination du meilleur compromis.
Une première version de ce document est parue dans la brochure Mathématiques, L’explosion continue réalisée par la Fondation Sciences Mathématiques de Paris (FSMP), la Société Française de Statistiques (SFdS), la Société de Mathématiques Appliquées et Industrielles (SMAI) et la Société Mathématique de France (SMF).
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
