
L’apprentissage profond : une idée à creuser ?
En effet, des scientifiques ont su médiatiser cette méthode avec des résultats expérimentaux spectaculaires. Cette approche a permis plusieurs avancées majeures : la plus connue est sans doute le programme de reconnaissance des visages de Facebook, récemment c’est la victoire d’AlphaGo qui a fait la Une, mais cela s’applique aussi à des secteurs comme l’automobile avec NVIDIA qui fournit des outils d’aide à la conduite assistée et autonome (ADAS), ou la santé avec la recherche de cellules cancéreuses par la start-up DreamQuark, ou encore la reconnaissance de parole.
Ici, en nous basant notamment sur l’ouvrage de Yoshua Bengio Learning Deep Architectures for AI et les travaux de l’équipe de Yann LeCun, nous souhaitons montrer les apports de cette construction scientifique multi-disciplinaire au machine learning ou « apprentissage automatique ».
Commençons par un exemple qui montre l’intérêt de ce formalisme. Précisons ensuite ce que calcule un réseau de neurones artificiels. Cela nous permettra de donner les idées-clés de l’apprentissage profond, des réseaux de neurones profonds et de leur complexité.
Apprentissage profond pour l’analyse de scènes
En associant l’apprentissage profond à des mécanismes algorithmiques de vision par ordinateur, il est possible d’analyser automatiquement une scène visuelle. Voici deux exemples tirés des travaux de Yann LeCun et de son équipe : tout d’abord, des scènes où il a été possible de reconnaître les objets (verdure sur-coloriée en vert, bâtiments en ocre et véhicules en magenta).

Source : Clément Farabet, Camille Couprie, Laurent Najman, Yann LeCun Learning Hierarchical Features for Scene Labeling (2013).
Autre exemple, cette scène panoramique urbaine où chaque objet est catégorisé.

Source : Clément Farabet, Camille Couprie, Laurent Najman, Yann LeCun Learning Hierarchical Features for Scene Labeling (2013).
Précisons que l’algorithme ne « comprend » rien, il ne fait que classifier. Le terme de route (road), bâtiment (building) ou personne (person) n’a pas de sens pour lui, ce ne sont que des étiquettes. Mais d’autres algorithmes peuvent être programmés à partir de ces données. Par exemple, cela permet à un système de surveillance d’autoroute, doté de milliers de caméras dont les flux vidéo ne sont humainement pas exploitables, de veiller au mieux à la sécurité des automobilistes. Cela pourrait aussi aider, par exemple, à identifier automatiquement les véhicules en cause suite à un accident.
Les mécanismes d’apprentissage profond ont fait leurs preuves en reconnaissance d’image, comme le montrent les exemples précédents. Les réseaux de neurones profonds, qui sont à la base de l’apprentissage profond, font aussi partie intégrante des systèmes de reconnaissance de parole ou encore de traitement du langage naturel, auxquels ils apportent une amélioration indiscutable. Voir par exemple la bibliothèque open source proposée par Google, TensorFlow, ou MonkeyLearn, ou aussi scikit-learn.
Comment ces mécanismes fonctionnent-ils ? Afin d’aider à la compréhension des éléments les plus théoriques, gardons à l’esprit l’exemple d’un système qui doit deviner quelles étiquettes poser sur une image.
Que calcule un réseau de neurones artificiels ?
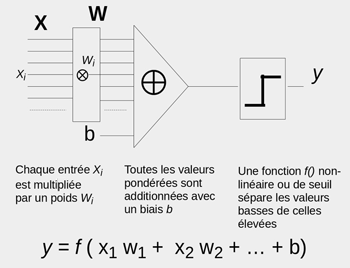
Un unique neurone artificiel est une « machine » très simple. À partir de plusieurs entrées, il produit une seule sortie. Les entrées (xi) sont mélangées, c’est-à-dire additionnées en pondérant chacune d’elles d’un poids wi positif (qui excite le neurone) ou négatif (qui inhibe le neurone), et en ajoutant au total une valeur b appelée biais. Une fonction seuil appliquée à ce total classifie le résultat comme valeur basse ou valeur élevée : si le total dépasse le seuil, le neurone « produit » une sortie, sinon il ne produit rien.
Un neurone unique effectue ainsi un calcul très rudimentaire de classification. Par exemple, un neurone avec deux entrées, qui prend en entrées les coordonnées d’un point dans le plan, détermine si ce point se trouve d’un côté ou de l’autre d’une droite donnée.
Considérons maintenant un réseau de neurones, le plus simple étant formé de deux couches. La première couche est constituée d’un ensemble de neurones, connectés en parallèle, et fournissant un ensemble de sorties y. Si ces sorties (y) sont maintenant combinées en étant les entrées d’un nouvel ensemble de neurones formant une seconde couche, nous obtenons alors un réseau de neurones à deux couches qui peut séparer un ensemble de données en deux. Nous verrons plus loin la possibilité de généraliser cette architecture et de passer d’un réseau à deux couches à un réseau à plusieurs couches.
Regardons maintenant comment un réseau à deux couches permet d’apprendre une fonction mathématique. Considérons une suite d’exemples, chacun constitué d’un ensemble d’entrées xi et de la sortie y attendue correspondante, que nous présentons au réseau. Durant cette phase dite « d’entraînement », le réseau va ajuster automatiquement les paramètres de chaque neurone, c’est-à-dire les valeurs des poids et du biais afin de minimiser l’erreur moyenne calculée sur l’ensemble des exemples entre la sortie attendue et celle observée. Il s’agit alors d’apprentissage supervisé puisque nous apprenons au réseau à fournir une réponse connue à l’avance. L‘hypothèse est qu’après cette phase d’entraînement, le réseau sera capable de traiter de manière satisfaisante de nouveaux exemples, dont la sortie est inconnue, en fonction de ce qu’il a « appris ». Il est à noter que plus le corpus d’exemples pour la phase d’entraînement est important, plus la précision du réseau sera élevée.
Ce type de réseau trop simple pour faire de la reconnaissance d’images peut néanmoins permettre de réaliser par exemple de la classification de données comme le propose le schéma suivant.
Si l’on considère un plan contenant des données, soit un espace à deux dimensions, un neurone seul réalisera une séparation linéaire de ce plan. La fonction mathématique qu’il représente est alors l’équation d’une droite séparant ce plan en deux, comme le montre le schéma ci-dessous à gauche.
Si les données, et donc le problème de séparation, sont plus complexes, la fonction mathématique sera non plus l’équation d’une droite mais une équation polynomiale de degré 3 par exemple. Un neurone ne sera pas suffisant, c’est un réseau de neurones qui réalisera cette séparation complexe du plan.
Dans l’exemple ci-dessous, l’augmentation du nombre de couches et du nombre de neurones accroît le pouvoir de séparation.
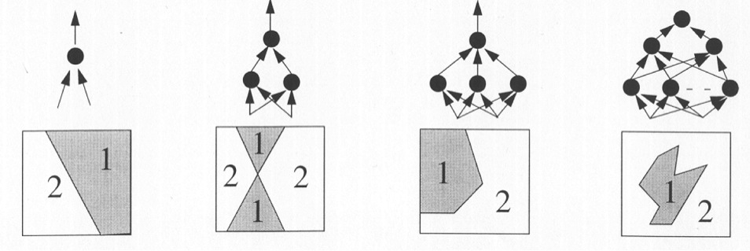
Schéma d’après Nicolas Rougier : Perceptron simple, Perceptron Multi-couches.
Selon sa structure, un réseau de neurones fournit une approximation de différents types de fonction. En effet, les réseaux à deux couches peuvent représenter des fonctions booléennes ou des fonctions continues, alors qu’un réseau à une couche ne permet de représenter que des fonctions booléennes.
L’idée forte de l’apprentissage par réseaux de neurones est de pouvoir, à partir d’un ensemble de calculs rudimentaires et locaux à chaque neurone, apprendre une fonction plus complexe.
On peut alors avoir l’impression d’ouvrir la voie à la création d’algorithmes universels, qui pourraient, avec suffisamment de mécanismes élémentaires, donc de neurones, et suffisamment d’exemples d’apprentissage, apprendre des fonctions aussi sophistiquées que voulu. Mais pourrait-on ainsi, en ajoutant des neurones et des couches, obtenir une approximation de n’importe quelle fonction mathématique ?
Dans les faits, cet espoir se heurte malheureusement à la malédiction de la complexité. On pourrait certes, théoriquement, obtenir une approximation de toutes les fonctions avec un réseau volumineux en termes de couches et de neurones, mais ce serait à condition d’utiliser un nombre déraisonnablement élevé de neurones.
Que se passe-t-il si le nombre de paramètres intervenant dans un problème et donc le nombre de dimensions augmentent ? Le nombre de neurones nécessaires pour calculer une telle fonction augmentera exponentiellement avec la complexité de cette fonction.
Si l’on reprend notre exemple d’étiquetage des images, et que l’on considère une image en couleurs de 300×300 pixels, nous aurions 90 000 pixels pour chacune des trois couleurs rouge, vert et bleu, soit 270 000 pixels au total. Si nous associons un neurone à chaque pixel, il faudrait déjà 270 000 neurones rien que dans la couche d’entrée.
Or ceci est tout simplement trop volumineux en termes de complexité de calcul, à l’heure actuelle, pour un réseau de neurones artificiels. Et il ne s’agit que d’une petite image ! Cela illustre le fait qu’un réseau comportant des millions de neurones n’est pas pour tout de suite.
Ce n’est du reste pas la seule difficulté. D’autres limitations importantes sont le nombre souvent faramineux d’exemples nécessaires pour apprendre les paramètres et le souci que ce qui a été appris sur ces exemples se généralise bien à tous les autres cas (en évitant de se baser seulement sur quelques cas particuliers).
Que pourrions-nous proposer pour fabriquer un système qui aurait un comportement satisfaisant avec un nombre raisonnable d’unités de calcul ? Serait-ce en utilisant des unités de calcul plus sophistiquées que ces neurones artificiels ? Ou plutôt en changeant l’architecture du réseau, c’est–à-dire ses connexions ?
Nous avons présenté ci-dessus un réseau dont l’architecture est simple : avec des connexions dans un seul sens, des entrées vers les sorties, et uniquement deux couches de neurones, essentiellement capable d’approximer des phénomènes linéaires.
Que se passerait-il si nous utilisions une architecture plus complexe ? Il existe en effet différentes manières de complexifier un réseau de neurones notamment en changeant la topologie en fonction du but recherché.
Le réseau peut par exemple comporter plus de deux couches. Il est alors qualifié de « multicouche » : avec une couche d’entrée, une couche de sortie, et une ou plusieurs couches cachées ou intermédiaires.
Le perceptron multicouche, capable de traiter des phénomènes non linéaires, est un exemple de ce type de réseau.
Un réseau de neurones peut aussi comporter des connexions récurrentes : il est alors doté d’une seule couche dans laquelle tous les neurones sont interconnectés afin de créer, par exemple, une mémoire adressable par son contenu. Mathématiquement, il correspond alors à une matrice de poids. Voir l’encadré ci-dessous.
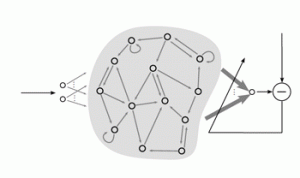
Par exemple, la figure ci-contre (d’après Mantas Lukosevicius et al. : Reservoir Computing Trends), représente un réseau avec un réservoir de calcul. Il s’agit d’une variante des réseaux de neurones qui a pour particularité, lors de sa phase d’apprentissage (d’entraînement) de ne calculer que les poids synaptiques des neurones de la couche de sortie. Ceux des autres neurones sont initialisés au hasard.
La phase d’entraînement est donc fortement simplifiée puisqu’elle est réduite à une simple opération de régression linéaire.
Dans cet exemple, le réservoir de calcul comporte des connexions récurrentes, à savoir entre les neurones, qui ne sont donc plus organisés en couches successives.
Cette approche a montré des résultats remarquables dans le cadre d’un exercice de reconnaissance vocale à partir d’une base de données de 500 chiffres (tous compris entre 0 à 9) prononcés par cinq personnes différentes, avec un taux d’erreur nul (d’après Juliette Raynal : Le réservoir computing dope l’intelligence des machines).
La théorie des systèmes dynamiques montre qu’avec des architectures aussi complexes, les comportements du système sont très riches même avec un nombre restreint de neurones artificiels. En contrepartie, les mécanismes d’apprentissage, au lieu de fonctionner très simplement comme pour les réseaux à deux couches, ne marchent tout simplement pas ! Dès que l’on ajuste l’un des paramètres, tout le comportement peut changer de manière chaotique (au sens mathématique comme au sens usuel du terme). Il est alors impossible de développer un algorithme d’apprentissage stable, sauf dans des cas bien spécifiques.
Un cas spécifique qui fonctionne : les réseaux de neurones profonds
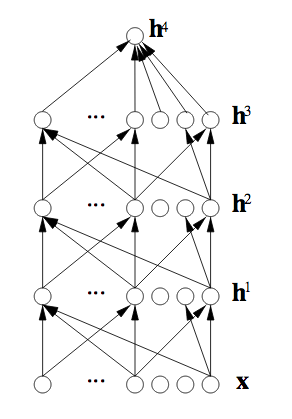
Un cas spécifique est celui des réseaux de neurones profonds (RNP). On garde ici l’idée de se limiter à des connexions d’entrées vers des sorties, mais l’architecture retenue consiste à empiler plusieurs couches, comme schématisé ci-contre (d’après Yoshua Bengio : Foundations and Trends® in Machine Learning). Les entrées, en bas, passent à travers plusieurs couches de calcul avant de produire une sortie, en haut.
La particularité des couches composant un RNP réside dans le fait que chacune d’entre elles est elle-même un réseau de neurones à part entière. Chaque couche — donc chaque réseau de neurones — prend en entrée les données de la couche précédente et sa sortie sert comme élément d’entrée de la couche suivante. Il est alors possible de jouer sur les différents paramètres de l’architecture du réseau : le nombre de couches, le nombre de réseaux qui composent chaque couche, le nombre de neurones dans chaque couche élémentaire de chaque réseau…
Entre la couche d’entrée et la couche de sortie du RNP, de nombreuses couches se succèdent donc. Il est difficile de mettre au point des mécanismes d’apprentissage efficaces pour chacune de ces couches intermédiaires (appelées couches profondes ou couches cachées). En présence de plusieurs couches, le risque est que seules les couches superficielles apprennent (ou sur-apprennent en réalité), les couches profondes restant incapables de s’adapter.
La solution proposée consiste à allier apprentissage supervisé (comme cela est fait pour un réseau à deux couches) et un apprentissage non-supervisé, c’est-à-dire un apprentissage utilisant des exemples dont la valeur de sortie est inconnue. Le mécanisme d’apprentissage supervisé tel que présenté précédemment est appliqué aux couches hautes, celles proches de la sortie du réseau, pendant que le mécanisme d’apprentissage non-supervisé est appliqué aux couches basses, celles proches des entrées.
Ce dernier mécanisme consiste à renforcer le poids des connexions entre deux neurones si leur activité est synchrone, c’est-à-dire s’ils sont actifs tous les deux en même temps, et à le diminuer dans le cas contraire (s’ils sont donc asynchrones). Ainsi, le réseau s’adapte afin de ne réagir qu’à des entrées similaires à celles déjà « vues » lors de l’apprentissage et ignorer les autres.
D’autres solutions existent, notamment celles qui s’inspirent du processus d’élagage du cerveau humain lors de son développement. Par exemple, à l’image d’un « jeune cerveau » qui se développe en supprimant des neurones, en enlevant des connexions ou en inhibant des réseaux existants, il est possible de contraindre l’architecture du réseau pour limiter le nombre de connexions à celles qui sont utiles, limitant l’apprentissage à celles-ci. Le but étant alors, tout comme le cerveau se sculpte sur mesure en fonction de ses expériences, que l’algorithme se sculpte lui aussi en fonction de son apprentissage.
Voici un schéma (très simplifié) de la circulation des données dans un réseau de neurones profond.
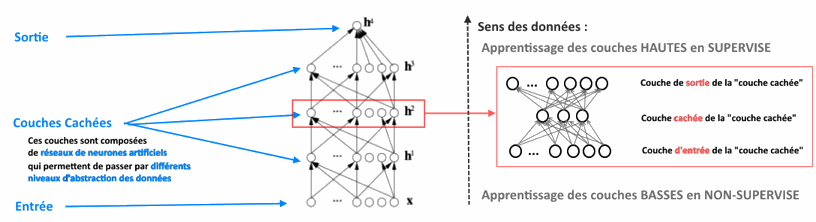
Schéma d’après Yoshua Bengio : Foundations and Trends® in Machine Learning.
Un tel travail à la chaîne permet ainsi à chaque couche de se spécialiser dans une partie du traitement de l’information, ceci via l’ajustement de ses paramètres.
L’alliance de méthodes d’apprentissage non-supervisé pour les couches basses, celles des entrées, et de méthodes d’apprentissage supervisé pour les couches hautes, permet une bonne capacité d’apprentissage.
Si nous reprenons notre exemple de l’image à étiqueter, les premières couches extrairont des caractéristiques simples (contours par exemple). Celles-ci seront combinées par les couches suivantes afin de former des concepts de plus en plus complexes et abstraits : assemblages de contours en motifs, de motifs en parties d’objets, de parties d’objets en objets, etc.
Des bases théoriques fructueuses ?
Un résultat théorique de 1991, dû à Johan Håstad et Mikael Goldmann, nous laisse à penser que les réseaux de neurones profonds reposent sur des bases fructueuses.
Les deux chercheurs suédois ont prouvé que retirer des couches d’un réseau de neurones artificiels faisait exploser la complexité. Très précisément, ils ont établi qu’« il existe une fonction calculable avec un réseau à k couches et N neurones par couche et dont le calcul avec un réseau à (k-1) couches demanderait environ 2N neurones. » Calculer cette fonction devient donc exponentiellement complexe si on retire une couche.
Ils ont démontré ce résultat dans le cas où tous les poids sont positifs et où les valeurs de sortie sont binaires. Il s’agit certes d’un résultat mathématique parfaitement démontré, il est cependant restrictif et non constructif.
- Le résultat n’est pas constructif : il ne donne pas le nombre minimum de couches pour une fonction donnée. Il n’indique même pas si ce nombre minimum existe. Il est donc nécessaire de tester numériquement, sur un grand nombre d’exemples, la profondeur à partir de laquelle les calculs sont possibles.
- Ce résultat s’applique dans un cas restrictif. Il n’a pu être démontré par les mathématiques que pour un type de réseau particulier : un réseau multicouche dont la caractéristique est d’avoir des circuits à seuils avec des poids positifs. En faisant l’hypothèse que ce résultat est vrai au-delà de ce cas spécifique, il est possible de le vérifier sur de nombreux exemples.
On constate ainsi numériquement, sans l’avoir prouvé mathématiquement, qu’il semble exister une profondeur idéale, c’est-à-dire un nombre de couches en-deçà duquel le nombre d’unités de calcul nécessaires augmenterait exponentiellement, et au-delà duquel les couches supplémentaires seraient inutiles, entraînant un délai de calcul trop long.
Le lien entre un résultat rigoureux et un travail expérimental sur des données est un trait caractéristique des sciences du numérique : elles allient des raisonnements mathématiques rigoureux à des hypothèses soumises à l’épreuve des simulations numériques pour tenter de les valider.
Conclusion
Inspiré des prouesses du cerveau humain, l’apprentissage profond est un modèle reposant sur une architecture informatique visant à mimer la « profondeur » des couches d’un cerveau, dans le sens où « chaque action est le résultat d’une longue chaîne de communications synaptiques » comme le dit Yann LeCun.
Le domaine de l’informatique inspiré par le cerveau humain, ou informatique cognitive, n’en est qu’à ses prémices. Bien que le deep learning soit devenu un buzz-word en moins de 3 ans, et qu’il soit déjà reconnu, utilisé et enseigné par les communautés scientifiques et informatiques, il reste encore beaucoup à faire dans ce domaine passionnant. Un fossé majeur subsiste avec ce que les humains peuvent réaliser instantanément. En particulier, le nombre d’exemples nécessaires pour l’apprentissage reste volumineux, et encore plus faramineux le nombre de neurones nécessaires pour obtenir une approximation des fonctions cognitives et biologiques.
[1] Site de référence des acteurs de la recherche sur ce sujet.
[2] L’intelligence artificielle n’aura pas lieu, Nicolas Rougier, Janvier 2015, blog L’« intelligence mécanique » de Scilog / Pour la Science
[3] Le “deep learning” pour tous ?, Rémi Sussan, Octobre 2014, InternetActu
[4] Foundations and Trends® in Machine Learning, Yoshua Bengio, Learning Deep Architectures for AI, Vol. 2, No. 1 (2009) 1-127 a servi de base à cet article.
[5] Machine learning, Wikipédia
[6] Réseaux de neurones artificiels, Wikipédia
[7] Reservoir Computing Trends, Mantas Lukosevicius, Herbert Jaeger, Benjamin Schrauwen, (2012) KI – Künstliche Intelligenz, Vol. 26, No 4, pp 365-371
[8] Deep Learning: Methods and Applications, Li Deng, Dong Yu (2014) Foundations and Trends® in Signal Processing: Vol. 7, No. 3–4, pp 197-387
[9] Learning Hierarchical Features for Scene Labeling (2013) Clément Farabet, Camille Couprie, Laurent Najman, Yann LeCun (2013) IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol 35, No, pp 1915-1929
[10] Réseaux de Neurones, Clément Chatelain
[11] Le réservoir computing dope l’intelligence des machines, Juliette Raynal
[12] Pour se développer, le jeune cerveau « élague », Christian Du Brulle
[13] On the power of small-depth threshold circuits, Johan Håstad and Mikael Goldmann. Computational Complexity, 1:113–129, 1991
[14] Les enjeux de la recherche en intelligence artificielle, Yann LeCun, sur Interstices
[15] Perceptron simple, Perceptron Multi-couches, Nicolas Rougier
[16] Non mathematical introduction to using neural networks, Jeff Heaton
[17] Deep learning : quand l’intelligence artificielle tente d’imiter le cerveau humain, Jérôme Cartegini
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

