
Comment désigner le vainqueur d’une élection ?
Le choix social
Une élection, c’est la situation de décision collective qui vous vient sans doute le plus souvent à l’esprit, que ce soit dans un contexte politique (élection d’un président, d’une assemblée) ou non (conseil de classe, d’administration…). Ces assemblées, conseils, ou autres comités, prennent eux aussi des décisions… en votant. Voici d’autres contextes avec moins d’enjeu : un groupe d’amis peut recourir à un vote pour décider de l’endroit et de l’heure d’un dîner, on peut recourir à Doodle pour trouver une date de réunion, une assemblée de copropriétaires peut avoir à statuer sur la réparation (ou non) de l’ascenseur.
Mais la décision collective va bien au-delà du vote ! Elle comprend également le partage équitable de biens ou de tâches, les appariements stables… Le champ d’activité scientifique qui s’intéresse à construire et à analyser des méthodes pour la décision collective s’appelle la théorie du choix social.
Quelques mots sur l’histoire du choix social
Pour être brefs (au risque d’être approximatifs), découpons l’histoire du choix social en trois grandes périodes. La période primitive trouve son apogée vers la fin du 18e siècle ; le lectorat français y retrouvera des noms dont il a sans doute entendu parler, et avant tout, le marquis de Condorcet, mais aussi le chevalier de Borda, qui gagnerait à être plus connu. Ces deux-là ne s’aimaient point… et sont tous deux à l’origine des deux familles (disjointes) de règles de vote les plus classiques !
Vient ensuite la période moderne, avec les premiers résultats dits « axiomatiques ». On peut dater sa naissance de 1951, avec la publication du théorème d’Arrow, qui ressemble à cela : dès qu’il y a au moins trois candidats, il n’existe pas de méthode pour agréger les préférences d’un ensemble d’individus qui satisfasse un ensemble de propriétés, qui pourtant paraissent toutes naturelles et souhaitables. Énoncer ces propriétés nous mènerait trop loin ; le lecteur intéressé pourra consulter Images des maths. Ce type de résultat, appelé théorème d’impossibilité, était le menu habituel des théoriciens du choix social de cette époque, qui pour l’essentiel venaient de la microéconomie ou des mathématiques.
Pendant cette période, personne ne pense à parler du calcul des méthodes ainsi caractérisées. Serait-ce parce qu’il ne pose aucune difficulté ? Pas du tout ! D’ailleurs, à partir du début des années 90, les informaticiens entrent dans la danse : c’est la troisième grande époque du choix social, avec l’émergence du choix social « computationnel » : l’utilisation de notions et techniques venant de l’informatique (en particulier l’intelligence artificielle, la recherche opérationnelle, l’algorithmique) permet non seulement de résoudre des problèmes classiques de choix social, mais aussi de les voir sous un angle différent, et au-delà, de prendre conscience de nouveaux problèmes.
Règle de la majorité
Un problème de vote consiste en un ensemble de candidats et un ensemble de votants, chacun d’entre eux ayant des préférences sur les candidats. Le but d’une règle de vote est de déterminer un candidat préféré collectivement.
Lorsqu’il n’y a que deux candidats (appelons-les A et B), il existe une règle évidente : la majorité. Lorsque plus de la moitié des électeurs votent A devant B, le vainqueur est A. En cas d’égalité, il faut départager les deux candidats.

Profil de vote
Avec trois candidats et plus, cela se complique !
L’hypothèse la plus classique en choix social (que nous ferons dans cet article, sauf tout à la fin) est que les votants expriment leur choix en classant tous les candidats par ordre de préférence décroissante. Chaque votant remplit un bulletin qui reflète ses préférences sur l’ensemble des candidats. Le bulletin n’autorise pas les ex-aequo et doit classer tous les candidats : il n’y a ni indifférence ni incomparabilité.
Il y a donc un grand nombre de bulletins possibles, autant que de classements possibles. Avec 5 candidats, on peut classer en premier un des cinq candidats, puis en deuxième un des quatre autres, etc., ce qui fait 5!=5x4x3x2x1=120 bulletins possibles (5! se lit factorielle 5).
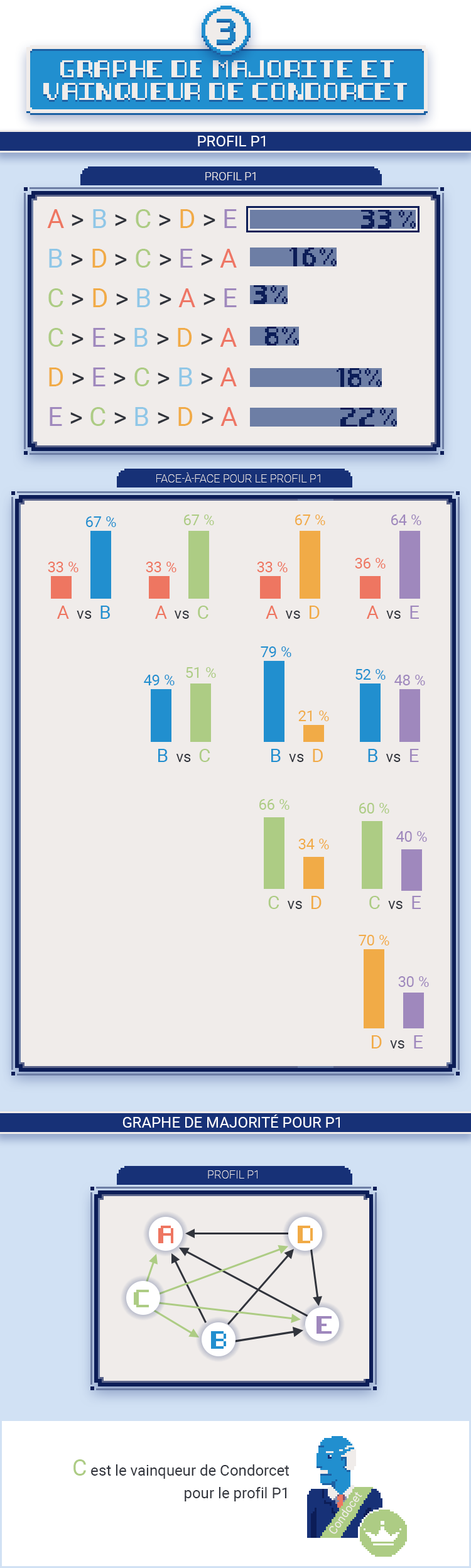
Lors du dépouillement, on rassemble tous ces bulletins pour former un profil d’élection. La figure ci-dessous illustre un bulletin de vote et un profil (noté P1) pour une élection avec cinq candidats.
Dans cet exemple, les votants n’ont choisi que 6 types de bulletins parmi les 120 possibles. Le profil indique la répartition des votes parmi ces 6 bulletins, tous les autres bulletins possibles ayant 0 % de voix.

Règles de vote
Comment désigner le vainqueur de l’élection ? Quelle règle de vote choisir ? Qui devrait être le vainqueur, selon vous ? Réfléchissez quelques instants avant de passer à la suite.
Graphe de majorité
On pourrait d’abord penser à généraliser le principe de la majorité établi pour deux candidats. Imaginons des face-à-face entre chaque paire de candidats. Grâce au profil (après dépouillement), on peut déterminer le vainqueur de chaque duel, en appliquant la règle de majorité. On établit ainsi une préférence collective entre deux candidats.
On peut représenter tous les duels par un graphe de majorité. Les sommets sont les candidats, et les flèches vont du vainqueur vers le vaincu du face-à-face.
Cela fonctionne-t-il ? Avec le profil P1, tout va bien. On trouve un chemin de préférence collective dans le graphe : C gagne contre tous les autres, puis B contre les autres sauf C, puis D, puis E, puis A.
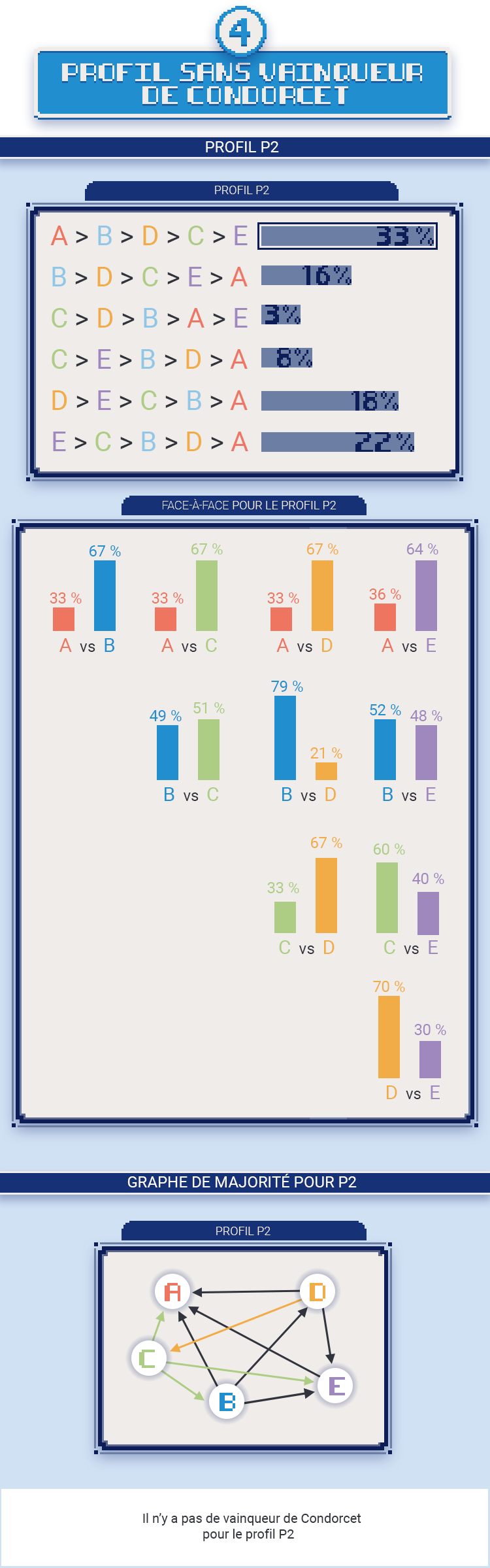
Mais ce n’est pas toujours aussi simple. Imaginons un autre résultat du vote avec encore les cinq candidats, avec un profil P2. Dans le graphe de majorité, aucun candidat ne gagne contre tous les autres. Il y a un cycle : C gagne contre B qui gagne contre D qui gagne contre C. Les trois candidats B,C,D gagnent contre trois autres, aucun ne gagne contre quatre.
Vous aimeriez sans doute appliquer une règle de vote pour déterminer qui est le vainqueur de l’élection pour les profils P1 et P2 !
Départage des ex-aequo
Sachant qu’une règle de vote désigne toujours au moins un vainqueur, il y a deux façons de définir une règle, selon que l’on exige ou non qu’elle dégage un vainqueur unique dans tous les cas de figure. Une règle de vote est résolue si, pour chaque profil, elle renvoie un candidat unique, appelé vainqueur ; tandis qu’elle est dite irrésolue si, pour certains profils, elle renvoie un ensemble de candidats ex-aequo qu’elle n’arrive pas à départager, appelés « co-vainqueurs ».
L’unique vainqueur sera choisi parmi les co-vainqueurs, au moyen d’une règle de départage des ex-aequo, soit déterministe (par exemple selon une priorité prédéfinie entre candidats, comme la priorité au plus âgé, ou entre votants, comme la priorité à la voix du chef), soit par tirage au sort. Il est souvent plus facile de définir d’abord la version irrésolue d’une règle, puis de définir ensuite sa version résolue comme la composition de sa version irrésolue et d’une règle de départage des ex-aequo.
Vainqueur de Condorcet
Souvenez-vous que nous avons parlé plus haut du marquis de Condorcet. On dira qu’un candidat est un vainqueur de Condorcet pour un profil P s’il gagne tous ses duels contre les autres candidats. Clairement, un seul candidat peut éventuellement gagner tous ses duels. Donc s’il existe un vainqueur de Condorcet, il est unique.
Regardons les cas des profils P1 et P2. Le vainqueur de Condorcet pour le profil P1 est le candidat C. Par contre, aucun candidat n’est un vainqueur de Condorcet pour le profil P2. On dira maintenant qu’une règle de vote (résolue ou pas) est Condorcet-cohérente si, dès qu’il existe un vainqueur de Condorcet pour un profil, la règle le désigne comme l’unique vainqueur de l’élection.
Exemples de règles
Règle de Copeland
La Condorcet-cohérence est une propriété intéressante : en effet, supposons que pour un profil de vote, C soit le vainqueur de Condorcet. Si la règle n’est pas Condorcet-cohérente et désigne un autre vainqueur pour ce profil, alors une majorité de votants pourrait à juste titre demander que le candidat élu soit remplacé par C. A contrario, l’élection de C est stable, car aucune majorité de votants ne tombe d’accord sur un candidat qu’elle préfère à C.
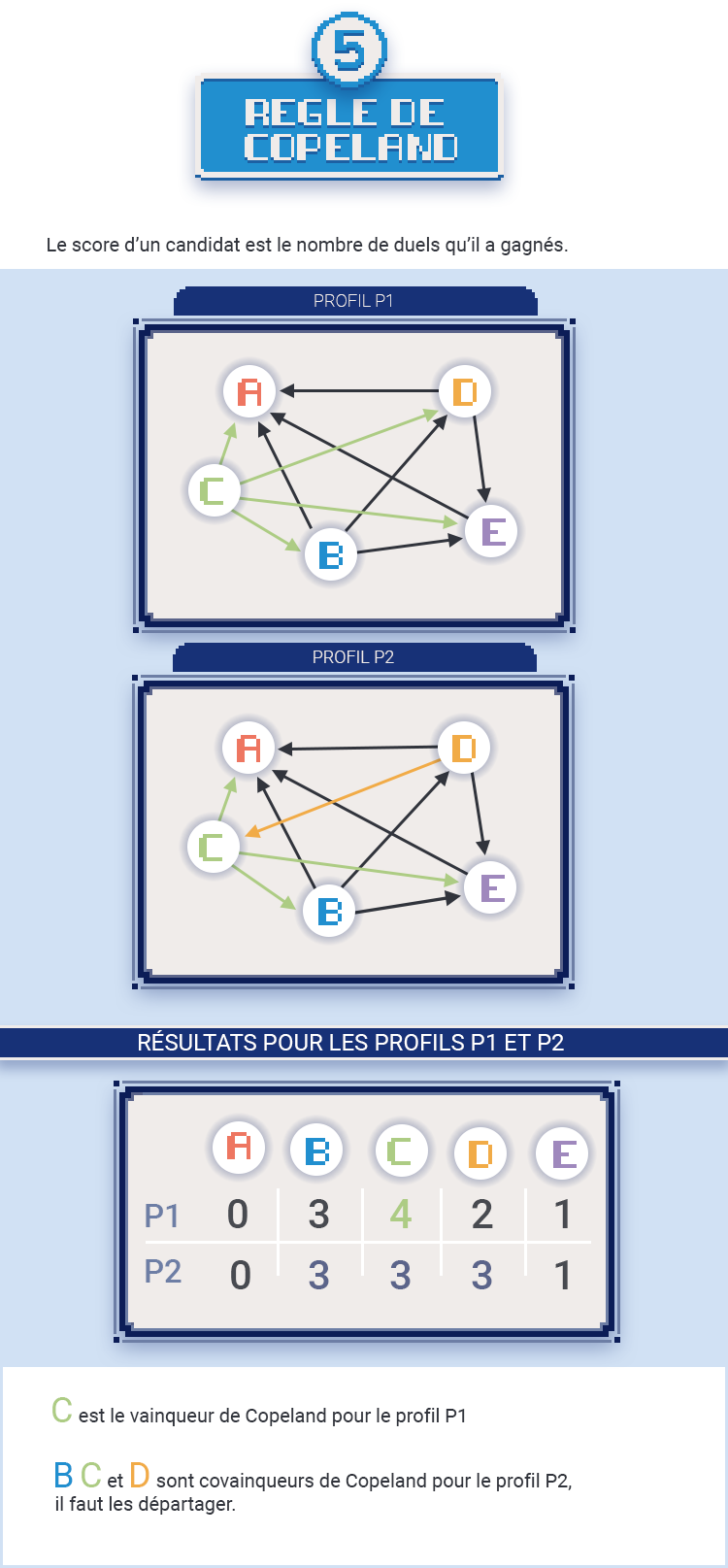
Voici une règle qui a cette propriété. À chaque candidat est attribué un score, dit de Copeland, qui est le nombre de duels gagnés (on peut les compter à l’aide des flèches du graphe de majorité). Celui qui a le score le plus élevé est vainqueur de Copeland. S’il existe un vainqueur de Condorcet, il est le seul dont le score est maximal (m−1 flèches avec m candidats). C’est donc l’unique vainqueur de Copeland et la règle est bien Condorcet-cohérente.
Ainsi, pour le profil P1, le vainqueur de Copeland est C ; pour le profil P2, il y a trois covainqueurs de Copeland (B,C,D).
Nous pourrions peut-être nous satisfaire de cette règle. Malheureusement, la Condorcet-cohérence est incompatible avec d’autres propriétés souhaitables, comme la participation et le renforcement. La participation postule qu’un électeur a toujours intérêt à voter. Considérons une élection où il s’abstient et où le candidat élu est A. Si l’électeur avait voté, soit A aurait été élu, soit c’est un candidat que l’électeur préfère à A qui aurait été élu. Le renforcement implique que si deux bureaux de vote élisent le même candidat B, alors la réunion de ces deux bureaux de vote élit aussi B. Ces deux propriétés sont, en revanche, satisfaites par d’autres règles, comme celles qui sont définies par un score basé sur la position dans les bulletins de vote, que nous allons voir maintenant.
Règles de score basé sur la position
Une règle de score basé sur la position attribue un score aux candidats, en fonction de leur classement dans les votes. À chaque place dans un bulletin est associé un score, qui diminue (ou reste le même) de la première à la dernière place (le score de la première place doit être strictement plus grand que celui de la dernière). Le score final d’un candidat est le cumul de ses scores dans chaque bulletin. Un vainqueur a le score le plus élevé.
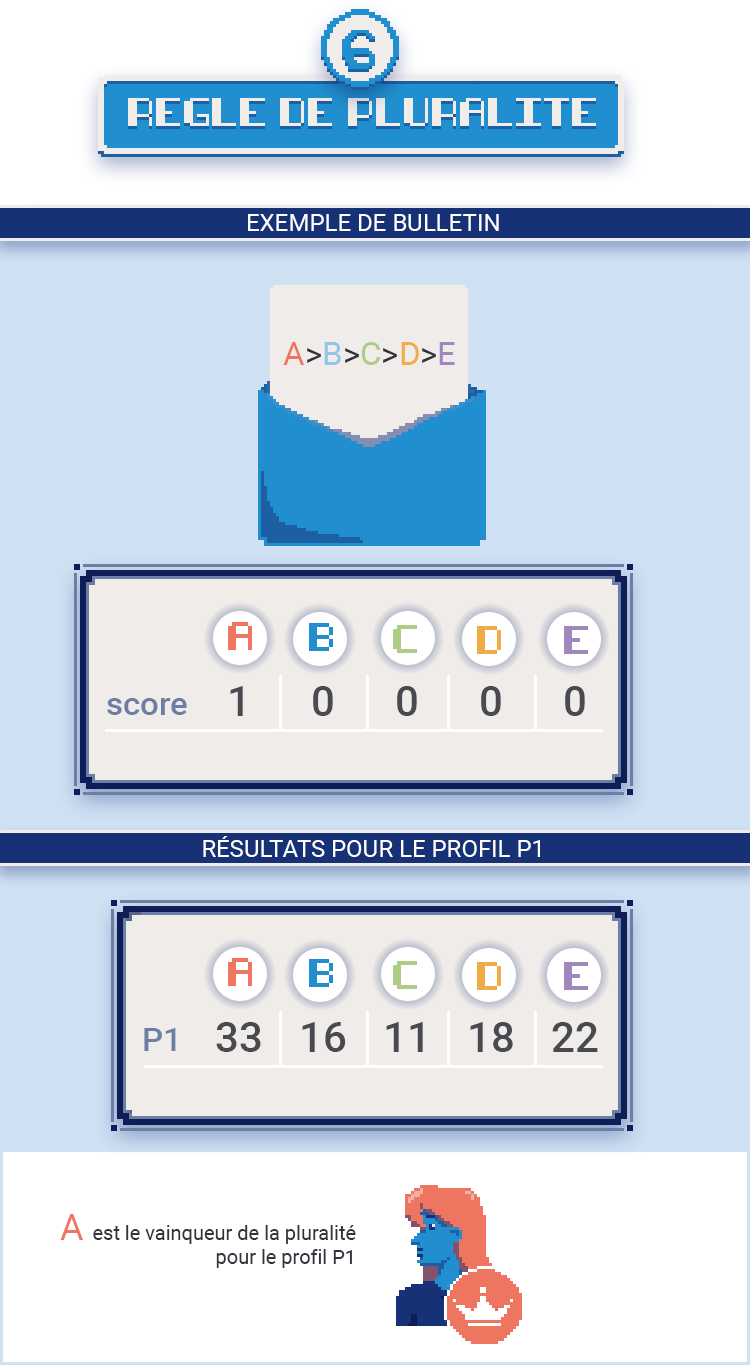
Une règle très connue est la règle de pluralité. Le score de la première place vaut 1, tous les autres scores valent 0. Le vainqueur est donc le candidat qui est le plus souvent classé premier.
Une règle moins classique est celle de veto. Cette fois, le score de la dernière place vaut 0, tous les autres scores valent 1. Le vainqueur est le candidat classé le moins souvent dernier.
Enfin, une troisième règle est celle de Borda (celui qui n’aimait pas beaucoup Condorcet). Lorsqu’il y a m candidats, le score diminue progressivement de m−1 pour la première place à 0 pour la dernière place. Tout le classement compte ici !

Souvenez-vous : pour le profil P1, le candidat C est le vainqueur de Condorcet. Mais ni la pluralité, ni la règle de Borda ne l’élisent, ce qui montre que ces deux règles ne sont pas Condorcet-cohérentes. Existerait-il d’autres règles avec un score basé sur la position qui le soient ? Hélas non, comme le montre Fishburn en 1979 avec l’exemple de la figure ci-dessous.
Il s’agit d’une élection avec trois candidats A, B, C et un profil P3 avec 17 votants. D’après le graphe de majorité, le candidat A est le vainqueur de Condorcet pour ce profil P3. Une règle de score basé sur la position est définie par trois scores. Quelles que soient leurs valeurs, pour le profil P3 cette règle attribue à B un meilleur score qu’à A, qui ne peut pas gagner l’élection.

Moralité : Aucune règle de score basé sur la position n’est Condorcet-cohérente. C’est bien dommage, parce que, par ailleurs, ces règles sont les seules à vérifier une panoplie d’autres propriétés satisfaisantes, dont le renforcement et la participation.
Règles à plusieurs tours
Il est difficilement imaginable, en France, de parler de vote sans évoquer la pluralité à deux tours (appelée aussi « scrutin majoritaire à deux tours ») : la règle de pluralité fournit les deux candidats qui ont le meilleur score (au besoin, une règle départage les ex-aequo). Le vainqueur est alors celui qui bat l’autre dans le duel à la majorité. Notons que les deux « tours » sont ici deux étapes de l’algorithme de calcul du vainqueur, et non pas deux tours « physiques » : les électeurs doivent soumettre leur ordre de préférence en entier, en une seule fois, et ne reviendront pas voter une seconde fois (alors que les deux « tours » comme on les pratique en France ont une tout autre signification : non seulement les électeurs votent deux fois, mais ils peuvent même changer d’avis, ce qui est exclu ici).

Une règle qui ressemble un peu à la pluralité à deux tours, appelée vote simple transférable (STV) est utilisée pour les élections politiques dans plusieurs pays, dont l’Australie et l’Irlande. La règle procède en m−1 tours, lorsqu’il y a m candidats. C’est la pluralité à deux tours s’il y a trois candidats. À chaque tour, la règle de pluralité fixe les scores. Le candidat avec le plus faible score, donc arrivant le moins souvent en tête, est éliminé et pour chaque bulletin, ses voix sont transférées au candidat préféré parmi ceux qui restent.

Aucune de ces deux règles n’est Condorcet-cohérente. Puisqu’elles sont souvent utilisées, on pourrait cependant imaginer qu’elles compensent cette violation de la Condorcet-cohérence par la satisfaction d’autres propriétés souhaitables… Las ! C’est loin d’être le cas. Non seulement elles ne satisfont ni la participation ni le renforcement, mais elles échouent à satisfaire une propriété qui est sans doute encore plus importante : la monotonie. Cette propriété exprime que si un votant fait « progresser » un vainqueur par un nouveau vote (sans rien changer d’autre), alors le vainqueur reste en tête.
Voici un exemple, avec 3 candidats et 17 votants, qui montre que la pluralité à deux tours ne satisfait pas la monotonie. Pour le profil P4, A est le vainqueur. Lorsque deux votants font progresser A d’une place, celui-ci est remplacé par B à la tête de l’élection.

Par contre, les règles de score basé sur la position satisfont la monotonie, ainsi que la grande majorité des règles Condorcet-cohérentes.
À chaque règle son vainqueur
Rappelez-vous : pour l’élection avec cinq candidats et le profil P1, cinq règles différentes donnent cinq vainqueurs différents. Saurez-vous associer règles et vainqueurs ?
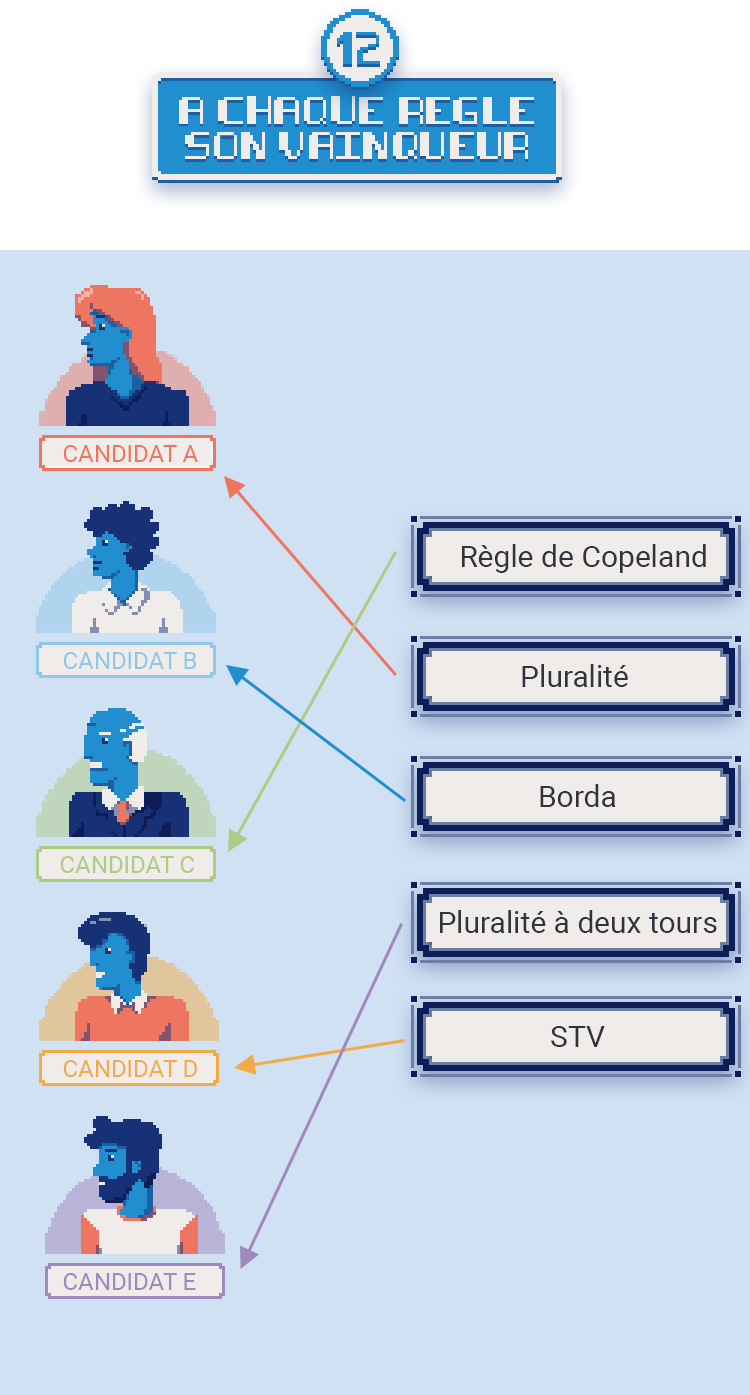
On le voit, le choix d’une règle de vote a une influence considérable sur le résultat !
Nous avons introduit plusieurs propriétés souhaitables des règles : la cohérence de Condorcet, la monotonie, la participation, le renforcement. Ces propriétés ne sont pas toutes satisfaites au sein d’une seule règle. Comment choisir ? C’est une question difficile à laquelle on ne peut pas répondre dans l’absolu : selon le contexte, certaines propriétés peuvent être plus importantes que d’autres. Il n’y a pas de mode de scrutin universellement bon, tous ont des défauts, pas toujours les mêmes, mais le scrutin majoritaire à deux tours en cumule vraiment beaucoup.

Dans les règles que nous avons détaillées, la détermination du vainqueur se fait à partir des classements que chacun des électeurs donne sur les candidats (ou parfois, à partir d’une partie seulement de ces classements, comme pour les règles de pluralité ou veto). Or, il existe des règles de vote pour lesquelles le contenu des bulletins est tout autre. Nous en citons deux : en vote par approbation, chaque votant spécifie le sous-ensemble des candidats qu’il approuve (ou, selon les interprétations : qu’il aime ; de qui il a une opinion positive ; qu’il accepterait de voir au poste de président ; etc.), et le vainqueur est celui qui est approuvé le plus souvent. En jugement majoritaire, chaque votant donne, pour chacun des candidats, une note sur une échelle qualitative (par exemple : « excellent », « très bien », « bien », etc.). Pour chaque candidat, on calcule alors sa note médiane, c’est-à-dire la meilleure telle que la moitié des électeurs donne une note au moins aussi bonne au candidat ; et le vainqueur est celui qui obtient la plus haute note médiane.
Les chercheurs en théorie du choix social conduisent des travaux de nature théorique mais aussi des travaux expérimentaux. Le but des expériences est de comprendre le comportement qu’auraient des électeurs si on les faisait voter selon un mode de scrutin ou un autre. Le premier tour de l’élection présidentielle de 2017 (comme cela a déjà été le cas en 2002, 2007 et 2012) sera l’occasion de faire de telles expériences, qui se dérouleront dans quelques bureaux de vote. Sur le site Vote au Pluriel, vous trouverez des détails sur les différents modes de scrutin, ainsi que des analyses sur les expériences menées en France en 2012, et dans d’autres pays. Grâce à la plateforme de vote en ligne Whale, vous pourrez organiser des votes entre amis et expérimenter plusieurs modes de scrutin.
Dans toutes les règles vues jusqu’à présent, le calcul du vainqueur se fait facilement. Mais voilà : d’autres règles intéressantes posent de délicats problèmes de calcul. Vous en saurez plus dans un prochain article d’Interstices !
Le Handbook of Computational Social Choice (F. Brandt, V. Conitzer, U. Endriss, J. Lang, A. Procaccia, eds.), Cambridge University Press, 2016, est librement téléchargeable. Voir en particulier le chapitre 2 (Introduction to the Theory of Voting, W. Zwicker).
Planches d’illustration réalisées par Victoria Denys, sur une conception de Jocelyne Erhel.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
