
Le transport optimal pour des applications en informatique graphique
Les histogrammes peuvent permettre de compter le nombre d’individus d’une population classée en catégories. Par exemple, une pyramide des âges représente le nombre de femmes et d’hommes catégorisés par tranche d’âge, et un sondage politique va compter les électeurs par orientation politique.
Il est important de pouvoir comparer des histogrammes, par exemple afin d’évaluer l’impact d’une mesure sanitaire sur la pyramide des âges (un vaccin, une lutte anti-tabac) ou d’un discours politique sur un sondage. Imaginons une société « vieillie » d’un an : sa pyramide des âges devrait être considérée comme similaire à sa pyramide initiale. Inversement, un baby-boom ou une épidémie peuvent modifier drastiquement cette pyramide.
Le transport optimal est une théorie mathématique offrant la possibilité de comparer de tels histogrammes, c’est-à-dire de définir une distance entre deux histogrammes. Ici, la distance avec l’histogramme de la population vieillie d’un an serait faible, alors qu’elle serait beaucoup plus importante dans le cas du baby-boom.
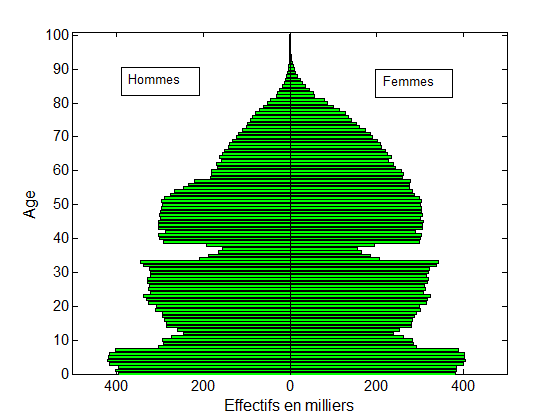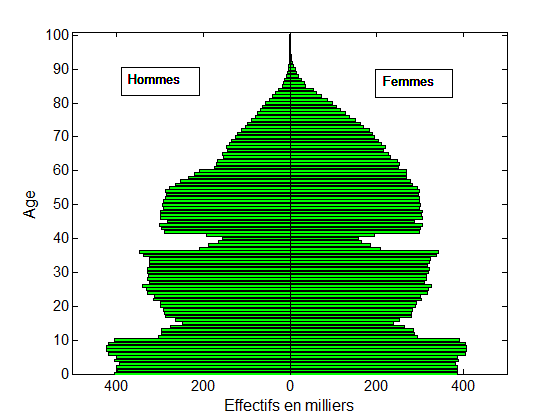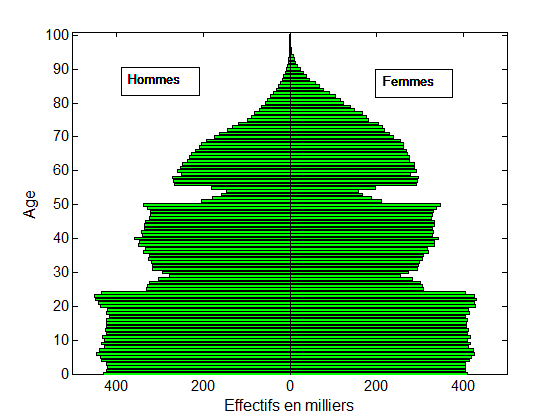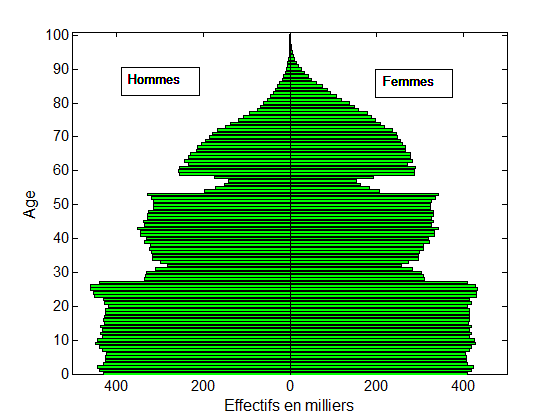
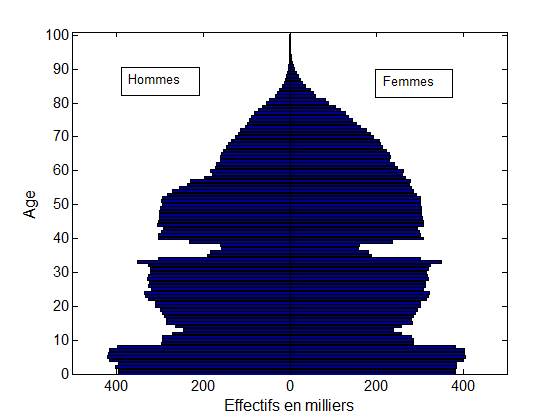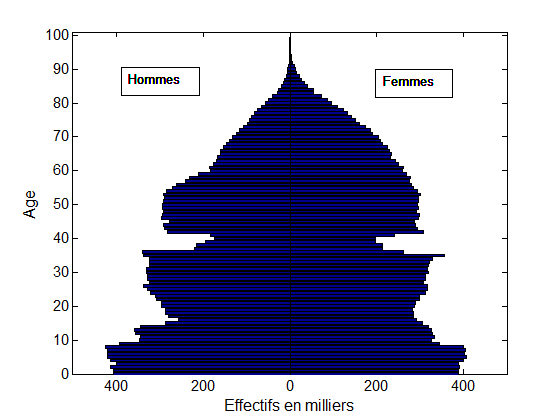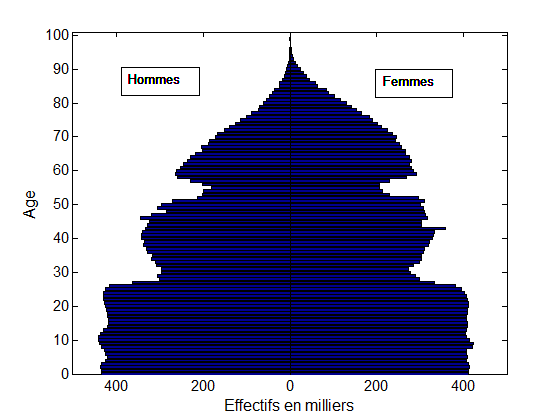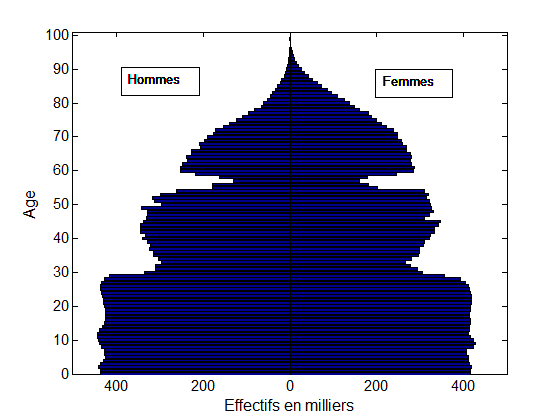
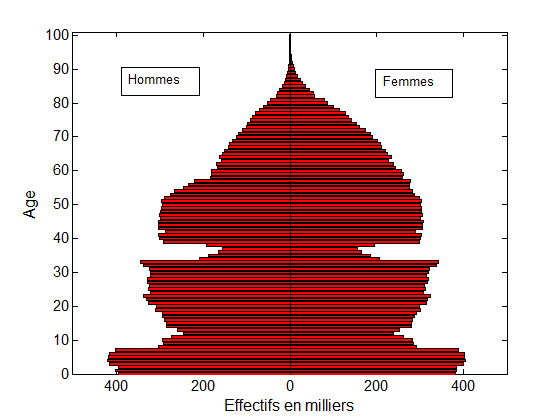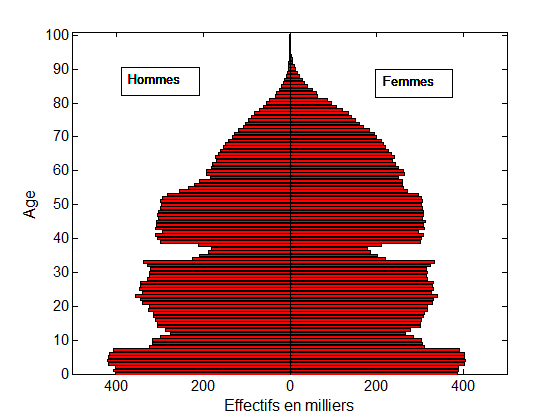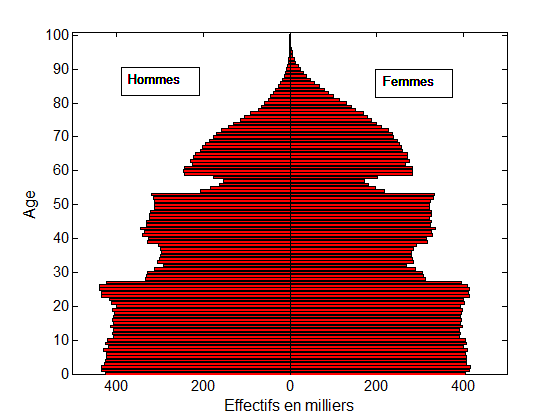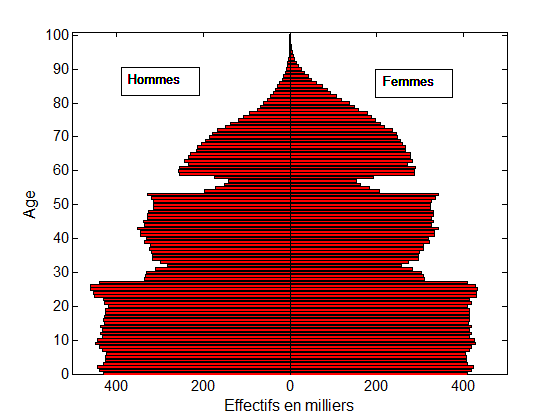
Plus encore, cette théorie permet d’essayer de prédire ce que serait un histogramme situé entre deux histogrammes donnés. Par exemple, étant données la pyramide des âges d’une population ne buvant pas d’alcool et celle d’une population buvant 4 verres d’alcool par jour, le transport optimal permet de prédire ce que serait la pyramide des âges d’une population buvant 1, 2, ou 3 verres d’alcool par jour. Ou encore, de prédire une pyramide des âges entre deux années distinctes (voir fig. 1 ci-dessous).
Référence |
Interpolation linéaire |
Interpolation par déplacement |
Fig. 1. Le transport optimal modélise le déplacement des creux et bosses de ces pyramides des âges entre 1954 et 1974. Les deux creux dus aux guerres mondiales se sont en effet déplacés de 20 ans (voir la référence en vert à gauche). Une interpolation linéaire entre la pyramide de 1954 et celle de 1974 (en rouge au milieu) ne permet pas un tel déplacement : une interpolation par déplacement (en bleu à droite) est plus appropriée.
Données : INSEE – Gilles Pison.
C’est ce que les mathématiciens appellent une « interpolation par déplacement » qui tire son nom du fait qu’elle « déplace » les histogrammes (voir fig. 2 ci-après, animation à droite). Au contraire, une interpolation plus classique (dite linéaire) ferait disparaître le premier histogramme progressivement au profit du second.
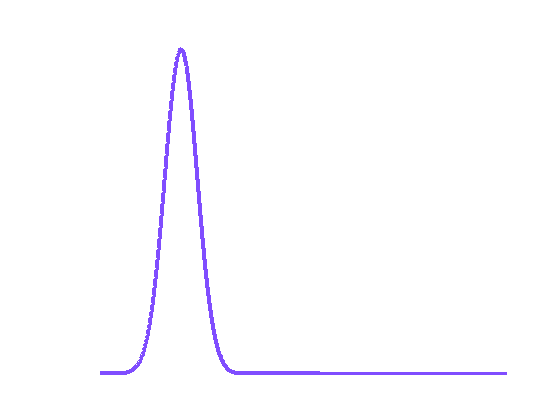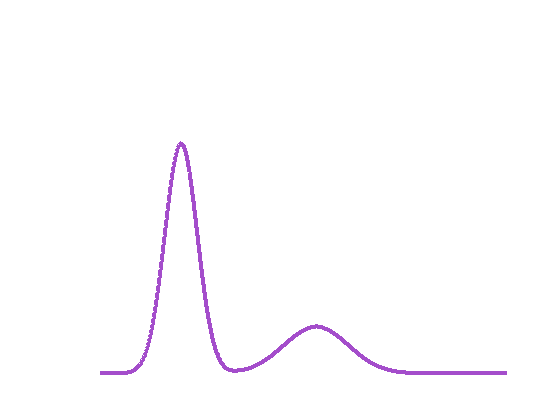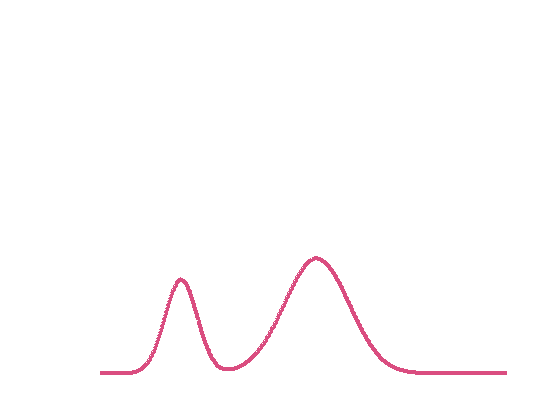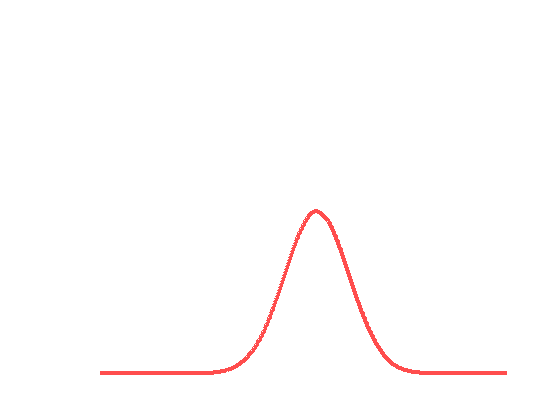
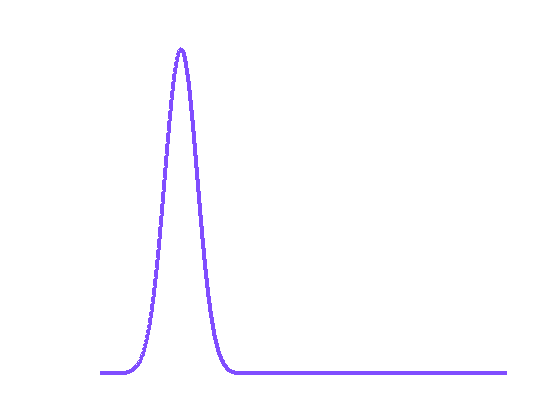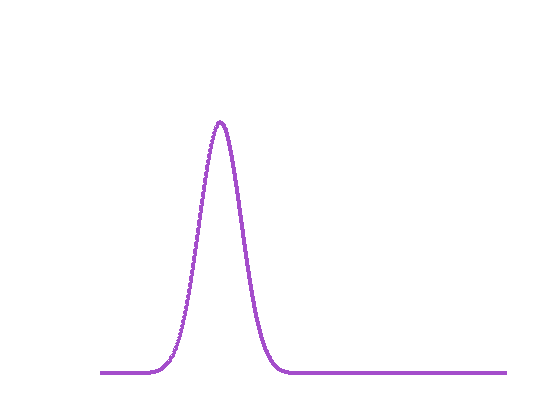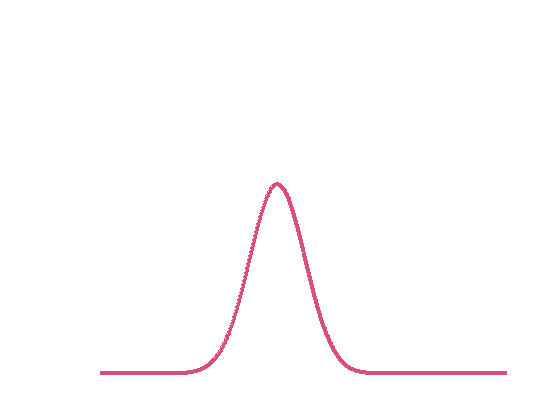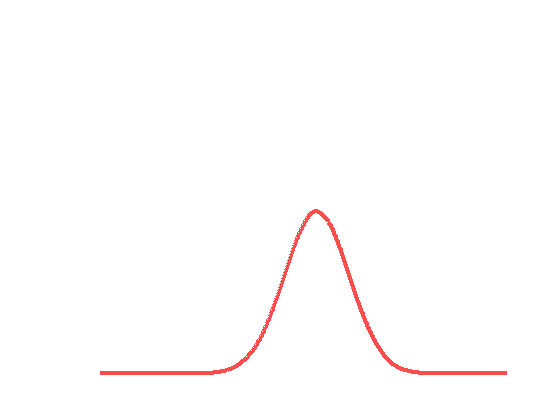
Fig.2 Interpolation entre deux distributions gaussiennes en bleu et en rouge. Le dégradé de couleurs indique la progression dans l’interpolation. L’interpolation classique (à gauche) fait disparaître la gaussienne en bleu pour laisser apparaître la deuxième en rouge, alors que l’interpolation par déplacement (à droite) transporte la première gaussienne en bleu vers la seconde en rouge.
Alors que l’interpolation par déplacement permet de prédire une pyramide des âges entre deux dates données car un vieillissement des populations a lieu, elle n’est pas appropriée pour interpoler entre la pyramide des âges des femmes et celle des hommes. Dans ce cas de figure, l’interpolation linéaire permettrait de prédire ce que serait la pyramide des âges d’une population qui contiendrait une certaine fraction de femmes et d’hommes, alors que l’interpolation par déplacement ne serait pas facilement interprétable.
Par ailleurs, les histogrammes sont généralement de dimension plus élevée. Ainsi, catégoriser une population à la fois par tranche d’âge, poids, taille et consommation d’alcool produirait un histogramme à 4 dimensions — chaque individu étant caractérisé par ces 4 données. La théorie du transport optimal est assez simple si on se limite à des histogrammes à une seule dimension, mais devient beaucoup plus complexe dès lors que l’on monte en dimensions.
Ainsi, le terme « population » est à prendre au sens large : une image est une population de pixels pouvant être catégorisés par couleur. Simuler le mouvement d’un fluide produit une population de particules caractérisées par leur position. Simuler l’éclairage d’une scène 3D produit une population de photons caractérisés par leur position, direction, énergie… C’est cette diversité qui fait l’attrait du transport optimal pour des applications en informatique graphique.
Calculer le transport
L’idée derrière la théorie du transport optimal, formulée initialement par le mathématicien Gaspard Monge en 1781, est de considérer les histogrammes comme des tas de sable que l’on doit déplacer d’un endroit à un autre. Calculer la distance entre deux histogrammes revient à calculer la distance totale parcourue par une équipe de travailleurs qui s’organiseraient au mieux pour transporter chacun une brouette de sable du premier histogramme pour reconstruire le second. Ces travailleurs se rendraient compte rapidement qu’ils feraient mieux de marcher en ligne droite et d’éviter de croiser leurs chemins pour marcher moins et minimiser l’effort collectif. C’est ce problème d’optimisation des trajectoires que formalise la théorie du transport optimal. Et c’est cette notion de déplacement de masse qui fournit une distance intéressante entre les histogrammes : ainsi, une pyramide des âges d’une population « vieillie » d’un an sera à une distance de 1 de la pyramide des âges initiale.
Il a cependant fallu attendre les travaux en 1942 du mathématicien Leonid Kantorovich (prix Nobel d’Économie en 1975) pour obtenir une méthode résolvant ce problème d’optimisation. Son idée consiste à chercher la quantité de sable déplacée entre chaque couple de position initiale et position finale, au lieu de chercher la destination finale de chaque travailleur. Cette simple modification permet de bénéficier du formalisme de programmation linéaire qu’il a développé trois ans plus tôt, et ainsi résoudre ce problème plus que centenaire.
Pourtant, ce n’est que très récemment que des méthodes efficaces se sont développées. Une de ces méthodes, appelée « méthode de Sinkhorn » fournit une approximation en quelques secondes (et seulement avec une poignée de lignes de code informatique) pour des problèmes qui auraient requis des semaines de calcul en utilisant de la programmation linéaire. Cette méthode simplifie le problème en « lissant » l’espace des solutions (ce qui a pour effet d’étaler un peu le sable transporté), permettant ainsi l’utilisation d’outils d’optimisation plus classiques.
Ce problème rencontre un certain succès en informatique graphique. Par exemple, étant donnée une photographie stylisée, aux couleurs intéressantes, il est possible de transférer ses couleurs à une photographie plus terne afin d’en raviver les couleurs. Pour cela, les travailleurs cherchent à déplacer des pixels (nos grains de sable) dans un espace de couleurs, partant de l’image terne et cherchant une destination adéquate parmi les couleurs de l’image vive. L’effort collectif étant minimal, il est alors plus probable qu’un vert terne se déplace vers un vert vif que vers un rouge vif, qui est beaucoup plus éloigné dans l’espace des couleurs.
L’interpolation par déplacement
Si tous les travailleurs déplaçant du sable décidaient de faire une pause à mi-chemin, en déposant le sable là où ils se trouvent, ils créeraient une nouvelle distribution de sable — un nouvel histogramme — qui se trouverait au milieu des deux histogrammes. C’est ainsi que l’on peut définir l’interpolation par déplacement, pour trouver par exemple la pyramide des âges de personnes consommant 2 verres d’alcool par jour connaissant la pyramide des âges de ceux n’en consommant pas et ceux en consommant 4 verres par jour. Si nous voulions la pyramide des âges à 3 verres d’alcool par jour, à la place nous ferions faire une pause à ces travailleurs aux trois-quarts de leur parcours (cf. fig. 2).
Cette notion d’interpolation par déplacement entre deux histogrammes a ensuite été généralisée à un nombre plus important d’histogrammes : il est dès lors possible de construire un histogramme qui soit une moyenne pondérée de trois histogrammes (ou plus). Pour construire cet histogramme « moyen » entre trois histogrammes, il suffit de construire un histogramme qui soit à égale distance de ces trois histogrammes.
De la même manière qu’on assigne des coefficients aux différentes notes des étudiants pour accorder plus d’importance à telle ou telle matière, on peut aussi assigner différents poids à chacun des trois histogrammes pour en favoriser un. Un tel histogramme intermédiaire est appelé « barycentre de Wasserstein », par analogie aux barycentres plus classiques.
Les coordonnées barycentriques
Étant donnés trois histogrammes, il est possible de calculer plusieurs barycentres de Wasserstein qui se situent entre ces trois histogrammes avec différents poids. On peut maintenant s’intéresser au problème inverse suivant : étant donné un quatrième histogramme, quels sont les poids tels que le barycentre de Wasserstein des trois premiers histogrammes ressemble le plus possible à ce quatrième histogramme ? Ici, « ressemble » peut se comprendre en termes de critères de ressemblance quelconques, tels que la distance du transport optimal par exemple, mais il peut y en avoir d’autres. Les poids obtenus définissent des « coordonnées barycentriques » et permettent de localiser un histogramme parmi un ensemble d’histogrammes.
Dans un article présenté à la conférence internationale SIGGRAPH consacrée à l’informatique graphique, nous exposons ce concept ainsi qu’une méthode résolvant efficacement ce problème. Il s’agit d’un algorithme d’optimisation basé sur la méthode de Sinkhorn, et ne requérant lui aussi qu’une poignée de lignes de code informatique et quelques secondes à quelques minutes de temps de calcul.
Une application particulièrement intéressante en informatique graphique est là aussi la manipulation des couleurs des images. Si nous possédons une photographie de paysage prise en été, aux couleurs verdoyantes, et que nous voulons lui donner un aspect plus automnal, nous pouvons télécharger une base de données de photographies de paysages différents pris en automne, et non plus une seule image comme nous avons vu précédemment, pour s’inspirer de leurs couleurs orangées. On cherchera alors les poids de chacune des images d’automne tels que leur barycentre de Wasserstein ressemble au mieux à l’image estivale (voir fig. 3 ci-dessous).
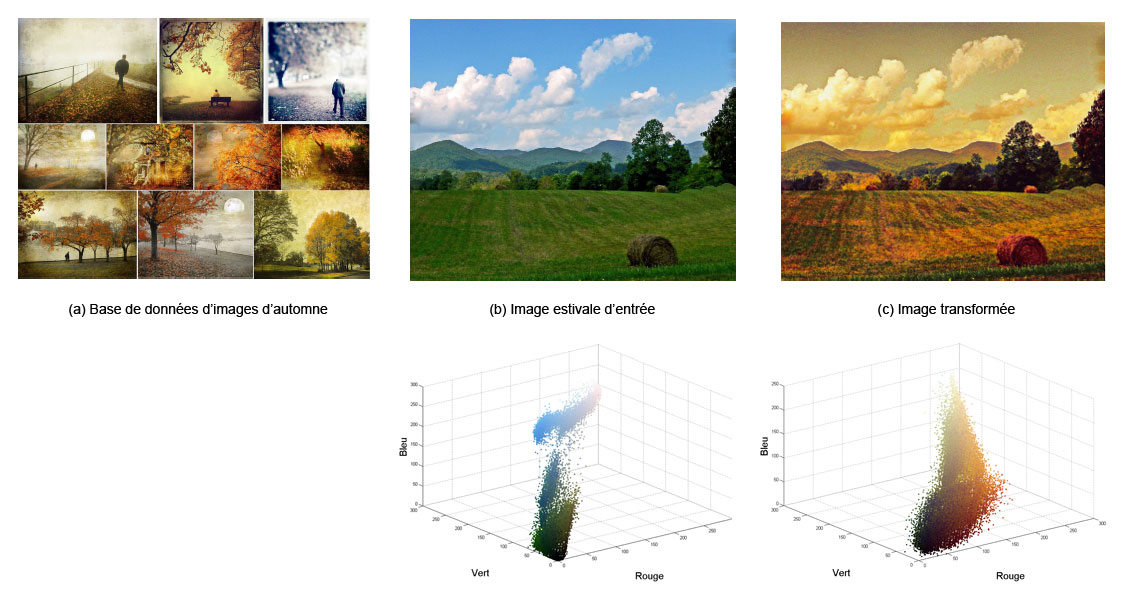
Fig. 3. Nous pouvons trouver la palette de couleurs la plus proche d’une image d’entrée (b) parmi une base de données d’images automnales (a) et ainsi la re-coloriser (c). Les histogrammes 3D sont représentés sous les images respectives.
D’autres applications ont été envisagées — par exemple compléter des données manquantes de mesures de matériaux ou de géométrie acquises par des scanners 3D, ou encore comparer un cerveau obtenu par imagerie médicale à une base de données de patients.
C’est finalement grâce aux progrès très récents dans l’efficacité du calcul numérique du transport optimal qu’a pu naître cette méthode. Nous espérons que notre méthode fournira un socle pour des développements en apprentissage automatique, problèmes inverses et autres régularisations de problèmes informatiques.
- La brouette de Monge ou le transport optimal, Yann Brenier. Interstices 2007.
- Wasserstein Barycentric Coordinates: Histogram Regression Using Optimal Transport, Nicolas Bonneel, Gabriel Peyré, Marco Cuturi. Siggraph 2016.
- Convolutional Wasserstein Distances: Efficient Optimal Transportation on Geometric Domains, Justin Solomon, Fernando de Goes, Gabriel Peyré, Marco Cuturi, Adrian Butscher, Andy Nguyen, Tao Du, Leonidas Guibas. Siggraph 2015.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Nicolas Bonneel
Chercheur CNRS au Laboratoire d'InfoRmatique en Image et Systèmes d'information (LIRIS).