
La course aux bits quantiques
Une première version de cet article est parue dans le hors-série n°107 de la revue Pour la Science , en mai 2020.
Le record actuel est à… 53 et il date d’octobre 2019. Ni température extrême en France métropolitaine ni vitesse (en noeuds) d’une planche à voile, nous parlons ici de qubits. Plus précisément, il s’agit du nombre de qubits qui équipent l’ordinateur quantique avec lequel Google a proclamé avoir effectué un calcul bien plus rapidement que les meilleurs supercalculateurs classiques. Contestée sur plusieurs points, cette annonce n’en est pas moins révélatrice d’une course effrénée que disputent acteurs académiques et privés, de la multinationale installée à la jeune start-up. Mais qu’entend-on par qubit ? Schématiquement, il s’agit de l’équivalent quantique d’un bit classique. Alors que ce dernier peut prendre comme valeur 0 ou 1, un qubit, jouant avec les propriétés étranges du monde quantique, est une superposition de 0 et 1. Un qubit peut alors représenter deux états, deux qubits correspondre à quatre… et ainsi de suite, N qubits équivalant à 2N états, soit pour les 53 qubits de l’ordinateur de Google, plus de 9 x 1015 états 0 et 1 !
À cette superposition s’ajoute une autre propriété essentielle des potentiels ordinateurs quantiques, l’intrication, un phénomène par lequel les états quantiques de deux entités, ou plus, comme des qubits, sont corrélés et donc dépendants les uns des autres. Intrication et superposition autorisent un parallélisme massif dans le traitement de l’information, la clé de la puissance de l’ordinateur quantique. Il y a toutefois un problème : la décohérence. Les interactions avec l’environnement font perdre ses propriétés à un système quantique, et ce d’autant plus qu’il contient de qubits. C’est contre elle que la course à l’ordinateur quantique est engagée depuis une vingtaine d’années. En résumé, la réalisation d’un ordinateur quantique repose sur le contrôle d’états intriqués s’étalant sur un nombre important de qubits et sur la préservation de la cohérence de tels états le plus longtemps possible.
Intrication et superposition autorisent un parallélisme massif dans le traitement de l'information
Aujourd’hui, le nombre maximal de qubits contrôlés est, nous l’avons vu, de l’ordre de la cinquantaine et le nombre d’opérations quantiques réalisées est du même ordre. C’est suffisant pour d’ores et déjà explorer un grand espace des états possibles à la limite de ce qu’il est possible de simuler sur les meilleurs supercalculateurs classiques. Les courbes de performance se croisent et les recherches sur la conception de qubits sont intenses. De nombreux candidats ont été testés : atomes, ions, molécules, électrons, photons, circuits supraconducteurs. Parmi eux, lesquels offrent les perspectives les plus intéressantes ?
Deux types d’ordinateurs
Pour répondre, il convient de distinguer deux types de machines quantiques : celles dotées de processeurs quantiques nécessitant des codes correcteurs d’erreurs et celles pour lesquelles le calcul est possible même avec un faible taux d’erreurs. Dans le premier cas, on parle de LSQ, pour large scale quantum computers, pour lesquels on cherche à pallier les erreurs liées à la décohérence, mais les chercheurs ont montré qu’il faudrait pour ce faire 1 000, voire 10 000 qubits physiques pour chaque qubit utilisable pour les calculs ! Un effort important est donc nécessaire pour résoudre le problème de contrôle posé par des processeurs quantiques à grand nombre de qubits.
Dans le second cas, on parle de NISQ, pour noisy intermediate scale quantum computers, c’est-à-dire des ordinateurs quantiques imparfaits de taille intermédiaire. Cette fois, la priorité sera une compréhension plus poussée des conditions de fonctionnement des qubits pour diminuer les erreurs lors des opérations quantiques.
Ces deux approches sont complémentaires et s’autoalimentent à mesure du développement des processeurs quantiques. Elles réclament toutes les deux un effort pluridisciplinaire combinant les sciences physiques, technologiques et informatiques. La diversité des perspectives de calcul suppose des prérequis différents au niveau des plateformes expérimentales, ce qui pourrait conduire à reconsidérer la notion selon laquelle une seule plateforme pourrait être universelle. Pour y voir plus clair, dressons un panorama des différentes plateformes en course, leurs forces et leurs limites, afin de comprendre pour quel type de calcul elles pourraient avoir un rôle à jouer à plus ou moins long terme.
L’élaboration d’un ordinateur quantique impose de lire individuellement les qubits, de les contrôler ainsi que leur interaction, dans un dispositif potentiellement intégrable à plus grande échelle. Parmi les innombrables systèmes issus de la physique ou de la chimie et gouvernés par des propriétés quantiques, ceux ayant atteint ces objectifs avec une précision suffisante sont rares, et c’est à eux que nous nous intéresserons ici. Précisons que cette sélection n’est valable qu’à un instant donné, aujourd’hui, et reste tributaire de nos connaissances, encore en construction, sur l’ordinateur quantique et de notre capacité à contrôler les systèmes quantiques. Le même exercice dans quelques années pourrait conduire à une liste différente.
Les qubits retenus se distinguent notablement en termes de performances et de géométrie, autant de caractéristiques liées à des paramètres physiques et technologiques, comme la vitesse et la robustesse des opérations quantiques, la taille effective du qubit, la variabilité des paramètres de fonctionnement du qubit… et aucun n’est pour le moment incontournable au vu des contraintes de l’ordinateur quantique.
| Supraconducteur | Spin dans silicium | Ions piégés | Photons | Atomes | |
| Taille | (100 µm)² | (100 nm)² | (1 mm)² | -(100 µm)² | (1 µm)² |
| Robustesse | ~99,3 % | >98 % | 99,9 % | 50 % (mesures) 98 % (portes) |
95 % |
| Rapidité | 250 ns | ~5 ns | 100 µs | 1 ms | 1 ms |
| Variabilité | 3 % | 0,1 % ~ 0,5 % | 0,0001 % | 0,5 % | 0,0001 % |
| Température d’opération |
50 mK | 1 K | 300 K | 4 K | 300 K |
| Connectivité | 4 | 4 | 10 | 2 | 10 |
| Nombre record de qbits intriqués |
53 | 2 | 20 | 18 | 51 |
Les performances des qubits se comparent sur la base de quelques caractéristiques essentielles. Du point de vue physique, les paramètres clés sont la taille effective du qubit, la robustesse face aux erreurs de calcul et la rapidité des opérations quantiques. D’autres caractéristiques, d’ordre technologique, sont surtout pertinentes pour le passage à grande échelle : la connectivité afin de réaliser des portes logiques à plusieurs qubits en une seule opération, la variabilité (des fréquences de Larmor), qui évalue l’effort à déployer pour calibrer les qubits et enfin la température d’opération. Pour chacun, le record du nombre de qubits intriqués est indiqué.
La voie du supraconducteur
La vitesse d’opération est clairement importante, car elle détermine la rapidité du processeur quantique. Si elle devient le facteur clé, alors le choix le plus judicieux est clair aujourd’hui : miser sur les qubits de type supraconducteur, c’est à- dire dépourvu de résistance électrique à basse température. L’étude de ces objets a commencé il y a plus de quarante ans lorsque diverses expériences ont montré le comportement globalement quantique du circuit supraconducteur le plus simple : la jonction Josephson. Cet élément est constitué de deux électrodes supraconductrices séparées par un mince isolant électrique que peuvent traverser, par effet tunnel, des paires d’électrons (dites « de Cooper »). Refroidis à des températures d’environ 20 millikelvins, les circuits à jonction Josephson se comportent comme des atomes artificiels à deux états possibles, le prérequis pour être un qubit.

Un circuit supraconducteur abrite en son centre neuf qbits. © Julian Kelly
La rapidité d’opération des qubits supraconducteurs résulte de leur taille. Au contraire d’autres systèmes, ils sont formés d’un nombre important de particules élémentaires, les électrons, qui se déplacent sans dissiper d’énergie dans des circuits de plusieurs centaines de microns. La taille des qubits supraconducteurs permet de bien les coupler aux sondes et excitations nécessaires pour les contrôler et autorise un temps de manipulation bien inférieur à la microseconde. À l’origine, les propriétés macroscopiques semblaient rédhibitoires pour élaborer des systèmes très résistants à la décohérence. Cependant, des efforts déployés pour comprendre et améliorer leur isolation vis-à-vis de l’environnement ont rendu les circuits supraconducteurs aussi performants que d’autres systèmes fondés sur des particules élémentaires individuelles, par essence plus isolés de l’environnement.
Les travaux ont initialement été menés dans des laboratoires académiques, puis plus récemment dans des laboratoires de recherche et développement de grands groupes industriels ou dans des start-up. C’est d’ailleurs la technologie retenue par Google, prouvant que des manipulations complexes et simultanées sur plusieurs dizaines de qubits supraconducteurs sont désormais possibles. De plus, les premiers protocoles de correction d’erreurs quantiques ont été mis en œuvre dans de tels systèmes à supraconducteurs.
Ce type de qubit est le système le plus avancé sur le marché des machines quantiques. Il a en outre l’avantage, dans la course vers les grands nombres qu’impose la voie du code correcteur d’erreurs, de compter sur des techniques de fabrication bien éprouvées. Cependant, les défis à relever sont nombreux. Ainsi, à courte échéance, les perspectives en termes de fidélité d’opération à plus grande échelle restent une question ouverte et on ignore encore si ces systèmes macroscopiques ne souffriront pas de limites intrinsèques. Ces dernières seraient notamment liées à leur température d’opération qui, à 20 millikelvins, est la plus froide possible. Des contraintes liées à la dissipation d’énergie générée par les signaux de contrôle deviendront de plus en plus importantes à mesure que le nombre de qubits augmentera. À très grande échelle, l’instabilité de ces qubits supraconducteurs sera le principal obstacle à franchir pour espérer les contrôler et les refroidir.
Le Qubit supraconducteur est le système le plus avancé sur le marché des machines quantiques
La voie du NISQ
Dans la voie de l’ordinateur quantique imparfait (le NISQ), la fidélité des opérations sur les qubits est un paramètre important. En effet, moins il y a d’erreurs, plus les systèmes sans correction d’erreurs pourront résoudre des problèmes de calcul avec un nombre moindre de qubits. Le choix se reportera alors sur des qubits fondés sur des particules élémentaires, et plus particulièrement ceux en environnement ultrapropre comme les ions ou les atomes neutres piégés sous vide dans des réseaux optiques. Le record actuel est à 20 atomes piégés intriqués.

Un ion de strontium (le petit point au centre, la fluorescence apparaît après un temps de pose de 30 secondes) a été piégé dans une enceinte ultravide entre deux électrodes. De tels ions piégés pourraient constituer des qubits. © D. Nadlinger/University of Oxford
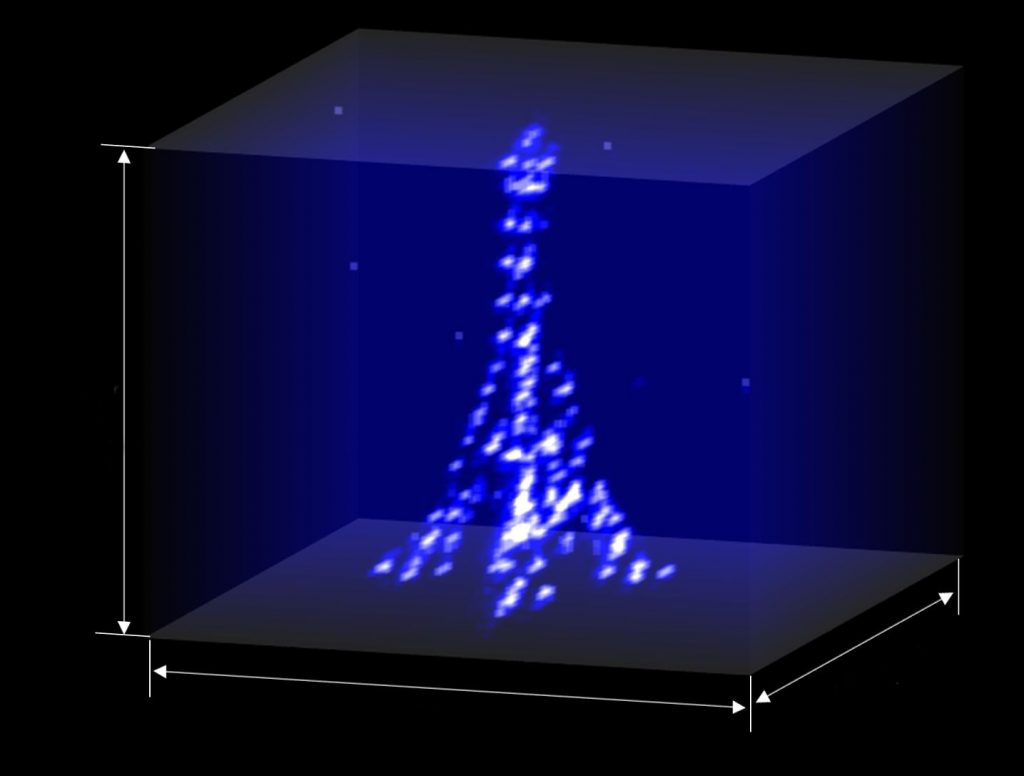
Des atomes neutres seraient de bons qubits si l’on pouvait les contrôler individuellement. C’est le cas dans cette tour Eiffel tridimensionnelle constituée de quelques atomes : un premier pas vers la conception d’ordinateurs quantiques à plusieurs centaines de qubits. © Institut d’Optique Graduate School, CNRS
La particule élémentaire est un électron de la structure atomique dont l’orientation du spin (un moment cinétique intrinsèque, de nature quantique) constitue l’état quantique que l’on manipule grâce à des lasers. Les ions et les atomes étant isolés dans le vide, ce type de qubit offre les temps de cohérence les plus longs, de l’ordre de plusieurs dizaines de minutes. Ils restent néanmoins contraints par des temps de manipulation assez longs, de l’ordre de la milliseconde pour la plus lente des opérations. Les efforts d’ingénierie portent aujourd’hui sur l’accélération du processeur quantique. Par rapport aux qubits supraconducteurs, les qubits atomiques ont l’avantage de fonctionner à température ambiante. On peut également faire interagir plusieurs qubits à la fois, ce qui ouvre des perspectives en termes d’optimisation des séquences d’opérations quantiques nécessaires pour un calcul.
L’avenir de ces systèmes repose sur des travaux menés au sein de laboratoires académiques et dans des start-up (IONQ, Alpine Quantum Technologies, Honeywell, Pasqal). Il s’agira surtout de développer des techniques de manipulation aussi avancées en termes de contrôle simultané que celles utilisées pour les qubits supraconducteurs. Restera aussi à passer à plus grande échelle, avec un effort en ingénierie plus difficile à évaluer que pour les systèmes de matière condensée.
La revanche du silicium
Après la vitesse et la fidélité des opérations menées sur les qubits, un autre point crucial dans le développement d’ordinateurs quantiques réside dans la possibilité des très grandes échelles (LSQ), au-delà du million de qubits. Une piste prometteuse se trouve du côté des qubits de spins dans les circuits semiconducteurs quantiques. L’élément de base est un électron individuel piégé électrostatiquement dans une structure semiconductrice, élément de base de l’électronique moderne permettant de sculpter à volonté le potentiel vu par les électrons. Le silicium est le matériau semiconducteur le plus célèbre, et on le trouve dans la plupart des microprocesseurs des ordinateurs classiques. De plus, cet élément se comporte comme un vide magnétique pour le spin ce qui protège efficacement le spin électronique des perturbations extérieures.

Dans ce qubit en silicium, le spin d’un seul électron (le point rose) a été intriqué à de la lumière (l’onde rose) et resté piégé dans une chambre à double-paroi. La lumière pourrait dans un futur ordinateur quantique transporter l’information concernant le spin de l’électron. © E. Edwards/Université du Maryland
Avec des tailles micrométriques de qubits, facilitant leur manipulation, et les capacités de la filière de la microélectronique du silicium, cette technologie a beaucoup d’atouts sur le papier en vue d’une intégration à grande échelle. D’autant plus que toutes les opérations élémentaires du calcul quantique sont accessibles et que les fidélités et les vitesses des opérations sont au rendez-vous. C’est remarquable, dans la mesure où les premières démonstrations de qubit dans le silicium datent de seulement huit ans. Toutefois, ces avantages méritent d’être renforcés de sorte que l’on puisse aller au-delà de deux qubits, l’état de l’art de cette technologie.
Beaucoup d’acteurs du domaine s’y emploient, que ce soit des laboratoires académiques, des services de recherche et développement d’entreprises installées (Intel) ou encore des start-up (Silicon Quantum Computing, Equal1). Notons que pour cette technologie, la part des ingénieurs, en l’occurrence en microélectronique, va bien au-delà de ce qu’on peut observer pour les autres systèmes en course en raison de la nécessité de s’appuyer sur des technologies éprouvées de la microélectronique pour améliorer la performance des qubits.
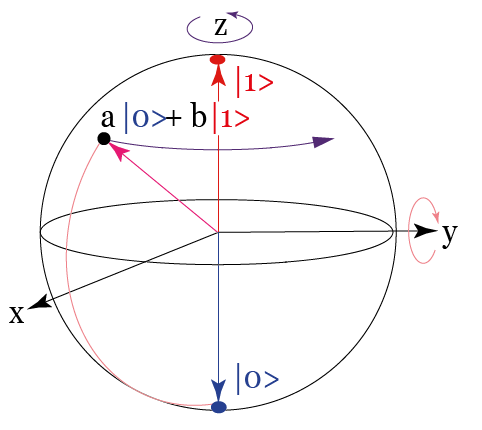
Dès le début de la course aux processeurs quantiques, les critères qu’un « bon » qubit doit satisfaire furent rapidement établis. Il doit être constitué d’un doublet d’états quantiques |0> et |1> et être initialisable de façon fidèle. En outre, il doit être muni d’une commande afin de réaliser (en un temps noté T1) n’importe quelle porte à un qubit (analogue quantique de la porte logique NON transformant 0 en 1 et vice versa). Ces portes se comprennent mieux à l’aide d’une représentation géométrique de l’ensemble des états quantiques a|0>+b|1> (a et b sont des nombres complexes) accessibles au qubit : la sphère de Bloch. Dans cette représentation (voir la figure plus haut), un état est une flèche pointant à la surface de la sphère (en magenta), les états |0> et |1> étant aux pôles, tandis qu’une porte se traduit par une rotation de l’état d’un certain angle autour d’un axe (en rose et en violet). Le qubit idéal doit aussi pouvoir être couplé à un autre qubit de façon à réaliser une porte logique à deux bits (en un temps noté T2). Cette porte doit être « universelle », dans le sens où tout algorithme quantique doit être décomposable en cette porte et en portes à un bit. Le qubit idéal est intégrable en grand nombre dans un processeur. La cohérence quantique des superpositions de ses deux états doit se maintenir durant un temps T3 bien supérieur aux temps T1 et T2 associés aux deux types de portes. Le qubit idéal est enfin muni d’un dispositif permettant de lire son état « en un coup », de façon fidèle. Qu’est-ce que cela signifie ? Dans la première étape d’une mesure, un qubit se trouvant initialement dans un état a|0>+b|1> finit toujours dans l’état soit |0>, soit |1> (on dit qu’il est « projeté »), avec les probabilités respectives |a|2 et |b|2. Le détecteur extrait alors de l’information du qubit pour déterminer cet état final et indiquer 0 ou 1. Quand il est suffisamment sensible pour que l’expérimentateur puisse lire sans équivoque le résultat, la mesure est dite « en un coup ». Dans le cas inverse, le même état initial doit être préparé et mesuré un grand nombre de fois, les mesures étant alors moyennées. Une lecture en un coup n’est jamais parfaitement fidèle, car le détecteur indique parfois 0 quand le qubit est projeté sur |1> et réciproquement. On la caractérise alors par sa fidélité, c’est-à-dire la probabilité de lire un résultat correct. Dans le cas idéal, la fidélité est de 100 %.
Et la lumière fuse
Les types de qubits que nous avons décrits sont fondés sur des particules massives et fonctionnent de façon très semblable : ils sont faciles à comparer. Ils constituent la grande majorité des systèmes candidats au calcul quantique à l’exception notable des photons intriqués, que l’on sait depuis longtemps produire et manipuler avec précision. Dans l’exploration de cette voie, les différences principales résident dans la nature évanescente du photon optique et dans la difficulté à faire interagir deux photons. La seconde propriété fait écho au caractère très isolé du photon ce qui en fait sans doute le système quantique individuel le plus cohérent et immune aux erreurs. Ces particularités rendent inapplicables les protocoles utilisés pour les particules massives où le caractère déterministe de l’interaction entre qubits existants sur des temps longs est primordial. Elles ont poussé la communauté à développer des protocoles spécifiques aux photons et à notamment augmenter le nombre de photons nécessaires pour définir un qubit. Ils reposent sur la conception de détecteurs à photons et sources d’états intriqués très efficaces. Un important effort de recherche, aussi bien dans des laboratoires académiques que dans des start-up (Quandela, PsiQuantum), est aujourd’hui consacré pour améliorer la performance de ces briques élémentaires.

Des qubits sous la forme de photons sont créés dans les spirales puis guidés le long de pistes en silicium pour effectuer différentes tâches. © X Qiang/Université de Bristol
Un pas important dans cette direction a été franchi ces dernières années avec des expériences quantiques à plusieurs photons dans des circuits photoniques en silicium. Cependant les premières démonstrations liées aux protocoles viables à plus grande échelle sont encore attendues, et elles devront être confrontées quantitativement aux exigences du calcul quantique. Arriver à se prémunir des limitations des photons pourrait conduire à l’émergence d’un système très cohérent avec peu d’erreurs, un pas important vers une machine NISQ efficace. Beaucoup de plateformes se développent et prétendent à concourir au titre de qubit idéal pour le calcul quantique. Elles sont portées par des acteurs des mondes académique et industriel. La course est lancée, mais aucun système ne semble prendre l’avantage, aucune échappée n’apparaît. On peut même imaginer que la diversité des applications du calcul quantique sera si importante qu’elle rendra nécessaire l’utilisation de différentes plateformes avec des propriétés physiques et technologiques distinctes. Et la notion de record de nombre de qubits perdra un peu de son sens…
A. CRIPPA ET AL., Gatereflectometry dispersive readout and coherent control of a spin qubit in silicon, Nature Communications, vol. 10, article 2776, 2019.
W. HUANG ET AL., Fidelity benchmarks for two-qubit gates in silicon, Nature, vol. 569, pp. 532-536, 2019.
F. ARUTE ET AL., Quantum supremacy using a programmable superconducting processor, Nature, vol. 574, pp. 505-510, 2019.
D. BARREDO ET AL., Synthetic three-dimensional atomic structures assembled atom by atom, Nature, vol. 561, pp. 79-82, 2018.
X. QIANG ET AL., Large-scale silicon quantum photonics implementing arbitrary two-qubit processing, Nature Photonics, vol. 12, pp. 534-539, 2018.
N. FRIIS ET AL., Observation of entangled states of a fully controlled 20-qubit system, Physical Review, vol. 8(2), article 021012, 2018.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Tristan Meunier
Chercheur CNRS dans l’équipe Circuits électroniques quantiques (Alpes), à l’institut Néel, à Grenoble.