La fin des Dames anglaises ?

Joueurs de dames anglaises.
De la collection de Jack et Beverly Wilgus.
Le jeu de Dames dans sa version anglaise, nommé aussi Checkers ou Draugths, se joue sur un tableau 8×8 et non pas 10×10 comme le jeu de Dames françaises, avec lequel il a de grandes similarités. C’est un jeu très pratiqué dans le monde anglo-saxon, aussi populaire que les Échecs, le Go ou Othello. Parmi ces quatre jeux, il était le plus susceptible de conduire à une victoire définitive de la machine. Espoir confirmé : il y a quelques mois, une équipe de chercheurs de l’Université canadienne d’Alberta a dévoilé une stratégie optimale pour ce jeu de Dames anglaises.
Le travail, coordonné par Jonathan Schaeffer depuis 1989, est un exploit historique qui a nécessité toutes sortes de compétences et un ensemble de calculs d’une incroyable complexité. Cette recherche a fait progresser le domaine de l’algorithmique des jeux et a permis la mise au point de techniques qui servent déjà dans d’autres disciplines. Contrairement à ce que l’on prétend, ce n’est pas une victoire de la machine sur l’homme, mais une victoire de l’intelligence humaine et de l’opiniâtreté de brillants chercheurs qui ont tiré des systèmes informatiques d’aujourd’hui un résultat étonnant, à l’extrême limite du possible !
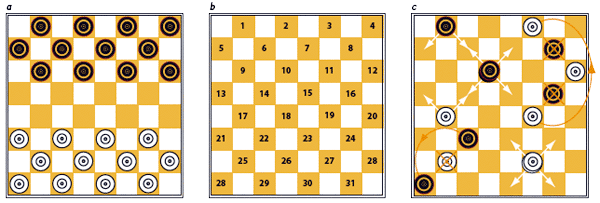
Le jeu de Dames anglaises se joue sur un damier 8×8 (a). On y dépose 12 pions blancs et autant de pions noirs. La numérotation des cases du damier sert à décrire les parties (b) ou la position (c) d’un problème (les Blancs gagnent). Dans une partie, les Noirs commencent. Le mouvement d’un pion se fait d’une case vers l’avant (vers les Noirs pour les Blancs et vers les Blancs pour les Noirs) en suivant les cases « noires ». Un pion prend un pion adverse (c) en sautant par-dessus, ce qui exige que la case d’arrivée soit vide. Plusieurs prises peuvent être faites successivement par un même pion lors d’un même coup. Les pions ne peuvent pas prendre en arrière. Lorsqu’un pion arrive sur la ligne adverse extrême, il devient Dame.
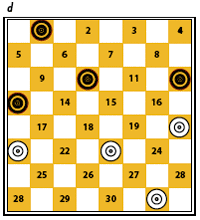
Contrairement au Fou du jeu d’échecs, les Dames ne « volent » pas : une Dame doit faire comme un pion et sauter les pions un par un en se posant derrière chaque pion pris ; les Dames peuvent se déplacer et prendre en arrière. Quand une prise est possible, le joueur est contraint de la faire. Quand plusieurs prises multiples sont possibles, le joueur n’est pas obligé de choisir la plus longue, mais il doit faire la prise choisie jusqu’au bout. Le jeu s’arrête quand un joueur n’a plus de pions ou ne peut plus bouger ; l’autre joueur a gagné. Dans la configuration (d) le premier qui joue gagne : ainsi Blancs gagne par 23-18, 1-5, 32-27, 5-9, 27-23. Pour le gain des Noirs, voyez un exemple ici. Une telle disposition est « marquée » dans le programme Chinook.
Il y a trois façons pour une machine de battre les joueurs humains à des jeux de tableau. La première méthode consiste pour l’ordinateur à jouer suffisamment bien pour que le joueur humain perde, ou fasse partie nulle, à chaque fois qu’il s’oppose à la machine. Le jeu de Dames anglaises se trouve dans cette situation depuis 1994. Le jeu d’Échecs est similairement maîtrisé depuis le fameux combat entre Garry Kasparov et la machine Deeper Blue en mai 1997. La supériorité de la machine sur l’homme aux Échecs a été confirmée en décembre 2006 par la victoire du programme Deep Fritz contre le champion du monde en titre Vladimir Kramnik.
Trois types de victoires
Cependant, une telle méthode n’interdit pas, en théorie, qu’un joueur humain particulièrement perspicace élabore une stratégie de jeu exploitant les points faibles du programme et réussisse ainsi à le battre. Les algorithmes utilisés pour écrire ces programmes de premier niveau sont fondés sur des « heuristiques », des procédés qui fonctionnent bien en général, mais dont rien n’assure qu’ils fonctionnent à tous les coups. Un bon jeu n’est pas un jeu parfait.
Pour obtenir des programmes qui gagnent infailliblement, un travail d’analyse plus fin est indispensable. Il faut en quelque sorte prévoir tous les coups possibles lors d’une partie. La machine n’a ainsi battu irrémédiablement le joueur humain que dans quelques jeux simples, dont le morpion sur échiquier 15×15 (nommé aussi Go-Moku) en 1996.
L’équipe de J. Schaeffer, déjà conceptrice du meilleur programme de jeu de Dames en 1994 (ce programme utilisait la méthode des heuristiques), vient de découvrir une stratégie de jeu infaillible. L’article publié électroniquement en juillet 2007 dans la revue Science s’intitule Checkers is solved, car la stratégie obtenue au final fonctionne parfaitement. Que le programme joue en premier (c’est-à-dire Noir) ou qu’il joue en second, jamais il ne perdra ; si l’adversaire du programme joue correctement, la partie sera nulle. Deux joueurs parfaits, par exemple l’ordinateur face à lui-même, feront partie nulle. Rien ne pourra modifier cette situation décevante, mais les spécialistes de ce jeu avaient pressenti depuis longtemps que l’opposition de deux joueurs parfaits donnerait un match nul.
La troisième façon pour une machine de bien jouer contre un adversaire consisterait à pratiquer une stratégie optimale de jeu quelle que soit la configuration initiale des pièces sur le damier, même s’il s’agit d’une configuration artificielle (plutôt que celle obtenue en suivant les règles du jeu). Ce troisième niveau de jeu, atteint pour le jeu africain Awari (ou Awele) en 2002, n’est pas à portée de main pour le jeu de Dames anglaises : quelques années supplémentaires seront nécessaires pour y parvenir.
Le nombre de configurations possibles des pions sur un damier anglais 8×8 est évalué à 5×1020, soit 100 millions de fois plus que le nombre de configurations possibles pour le jeu Awari. C’est la première fois qu’un jeu de cette difficulté est résolu complètement. On remarquera que c’est encore le nombre 1020 qui marque la limite des capacités technologiques actuelles. Ce nombre est celui de la mémoire artificielle : la mémoire cumulée des disques durs d’aujourd’hui sur Terre avoisine 1020 octets, et dans le domaine de la puissance de calcul, la puissance cumulée des microprocesseurs sur Terre est aujourd’hui évaluée à environ 1020 instructions par seconde. Ces capacités cumulées suivent la loi de Moore : elles sont doublées, au moins, tous les 18 mois, ce qui est équivalent à une multiplication par 10, au moins, tous les cinq ans. Peut-être en est-il de même pour la taille de l’arbre des jeux dont on peut déterminer les stratégies optimales.
Pour réaliser son exploit, l’équipe canadienne a décomposé le problème en plusieurs étapes, certaines ayant exigé des années de travail et des milliers d’heures de calculs. Précisons que la méthode utilisée ne consiste pas à représenter dans les mémoires d’un ou de plusieurs ordinateurs l’ensemble des 5×1020 configurations possibles, puis, après avoir analysé cet ensemble, à en déduire la stratégie optimale. Cette méthode d’exploration exhaustive du jeu par analyse rétrograde (mathématiquement bien définie et parfaite en théorie) exigerait un espace de stockage supérieur à l’ensemble de la mémoire numérique disponible aujourd’hui sur Terre ! Il a fallu être plus subtil…
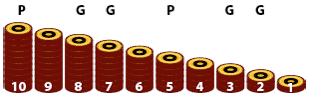
Pour comprendre la méthode de marquage rétrograde, nous allons analyser le jeu très simple qui suit. Une pile de 10 pions est posée sur une table. Deux joueurs jouent à tour de rôle et doivent à chaque tour prendre 2 ou 3 pions de la pile. Ils n’ont pas le droit de passer. Celui qui prend le dernier pion a gagné à moins qu’il ne reste qu’un seul pion, auquel cas la partie est nulle. Il y a dix positions (configurations) possibles.

L’analyse rétrograde a pour objectif de marquer chaque configuration du jeu par G (pour gagnante), P (pour perdante) ou N (pour nulle). Par définition, une configuration gagnante G est une configuration telle que celui qui doit jouer peut, en jouant bien, gagner la partie quel que soit le jeu de son adversaire. Une configuration perdante P est une configuration telle que celui qui doit jouer ne peut éviter de perdre si son adversaire joue bien. Une configuration nulle N est une configuration où celui qui doit jouer ne peut pas gagner si son adversaire joue bien, mais ne perd pas non plus si lui joue bien ; c’est donc une configuration qui conduit à une partie nulle lorsque les deux joueurs jouent au mieux.
L’analyse rétrograde part des configurations les plus simples et remonte progressivement vers les positions les plus complexes. Par la règle du jeu, la configuration 1 est nulle. Les configurations 2 et 3 sont G, car celui qui joue gagne s’il reste 2 pions (il les prend) ou s’il reste 3 pions (il les prend).

La configuration 4 est N, car s’il me reste 4 pions et que je dois jouer, j’en prendrai 3 (ce qui conduira à une partie nulle), plutôt que 2 (ce qui ferait gagner mon adversaire).
La configuration 5 est P, car s’il reste 5 pions et que je dois jouer, je ne peux éviter de placer mon adversaire dans une position gagnante (3 ou 2 pions).
La configuration 6 est N, car s’il reste 6 pions et que je dois jouer, je préférerais une partie nulle (en prenant 2 pions et en laissant 4 pions) qu’une partie perdante (en jouant 3 et en laissant 3). À partir de la position 6, comme à partir de la position initiale du jeu de Dames anglaises, deux joueurs jouant bien feront partie nulle.
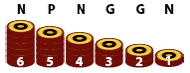
Les configurations 7 et 8 donnent accès à 5 qui est P : elles sont G.

La configuration 9 est N et la configuration 10 est P.

Une fois le marquage terminé, jouer parfaitement est facile. Si vous êtes dans une position G, il existe une façon de jouer qui place votre adversaire en position P, c’est bien sûr celle-là que vous choisirez. Si vous êtes en position N, vous ne pouvez accéder à aucune position P, mais il existe au moins une position N que vous pouvez atteindre : vous la choisirez. Si vous êtes en position P, quoi que vous fassiez, votre adversaire se trouvera en position G, et donc pourra vous remettre en position P, ce qui, de proche en proche, vous conduira à la défaite.
Ce type de marquage est possible en théorie pour les jeux de Dames, d’Échecs, d’Othello, etc. On est donc certain qu’il existe des stratégies optimales pour ces jeux, même si personne n’est en mesure de les calculer. Pour les déterminer, il faut marquer la position de départ. Notons, car c’est essentiel, qu’il n’est pas nécessaire de marquer l’ensemble des configurations possibles pour connaître le marquage de la position de départ et pour jouer parfaitement. En effet, pour chaque position G, il suffit de connaître une possibilité de jeu plaçant l’adversaire en position P, ce qui autorise à négliger toutes les autres possibilités de jeu.
Organiser un calcul de marquage de façon à avoir suffisamment d’informations pour prouver que la position initiale est G, P ou N et pour ensuite jouer de manière optimale est donc assez subtil. C’est parfois possible, même si l’ensemble de configurations du jeu est trop grand pour être entièrement exploré et marqué, ce qui est le cas de tous les jeux cités.
L’équipe de chercheurs de l’Université d’Alberta vient de réussir le marquage de la position initiale du jeu de Dames anglaises. Le marquage de la position initiale a été prouvé N. La partie de l’ensemble des configurations marquées pour arriver à ce résultat est infime (107 configurations) par rapport à l’ensemble des configurations du jeu (5×1020configurations). Trouver ce judicieux sous-ensemble a été un travail de titan.
Dans notre exemple, on peut savoir avec certitude que la position initiale est P en ne connaissant que les marquages suivants qui assurent que chaque P ne donne accès qu’à des G, et qu’à partir de chaque G, on a accès à au moins un P.
La longue histoire de Chinook
Le projet a débuté en 1989. Au début, l’objectif était de développer un programme capable de battre le champion du monde en titre, Marion Tinsley, qui dominait le jeu depuis 1950. Entre 1950 et sa mort en 1995, Tinsley gagna tous les tournois auxquels il participa et ne perdit jamais aucune partie contre des humains en tournoi. C’est dire à quel point il dominait la discipline !
L’objectif de le battre ne fut pas atteint en 1992, année où le programme Chinook de l’Université d’Alberta perdit un tournoi officiel contre Tinsley (le Chinook est un vent chaud qui descend des montagnes et qui se réchauffe par la compression résultant de la diminution d’altitude). Lors de ce tournoi, Tinsley s’inclina cependant deux fois devant la machine ; c’était donc ses premières parties perdues dans un tournoi depuis 1950. En 1994, un second tournoi entre Chinook (amélioré entre-temps) et Tinsley fut organisé. Ce tournoi fut interrompu à cause de l’état de santé de Tinsley ; il était atteint d’un cancer du pancréas qui l’emporta huit mois plus tard. Depuis, le programme Chinook est reconnu comme le meilleur joueur, et tous les humains qui s’y sont confrontés ont perdu contre lui. Cette situation peu satisfaisante – Marion Tinsley aurait-il battu Chinook ? – a incité l’équipe de J. Schaeffer à aller plus loin. Cette fois, le but fixé était l’élaboration d’une stratégie optimale de jeu qui assurerait mathématiquement que jamais aucun humain, pas même Tinsley, ou aucune autre machine ne remettrait en cause la domination des nouvelles versions, parfaites, de Chinook.
Pour un jeu simple, on trouve les stratégies optimales en utilisant la méthode d’analyse rétrograde. Les configurations finales correspondant à des parties terminées sont marquées gagnante (pour celui dont c’est le tour de jouer) perdante ou nulle selon les cas. Ce marquage permet de connaître la nature perdantes, gagnantes ou nulles des configurations qui précèdent un coup. Puis, pas à pas, en remontant, on marque des configurations de plus en plus complexes et proches du début de la partie. Dans le cas des jeux élémentaires, on peut remonter jusqu’à la position initiale dont on sait alors si elle est gagnante, perdante ou nulle.
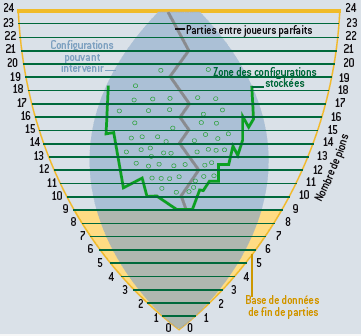
Schéma général de l’exploration.
Recherche d’un marquage de la position initiale du jeu de Dames anglaises par l’équipe de chercheurs de l’Université d’Alberta. Le nombre de pièces présentes sur le damier est représenté sur l’axe vertical, le nombre total de positions est donné en échelle logarithmique sur l’axe horizontal. La zone rosée représente l’ensemble des fins de parties (toutes les configurations de 10 pièces ou moins) dont la liste complète a été calculée, marquée (gagnante, perdante ou nulle) et stockée. La zone ovale bleue représente la partie de l’espace réellement utile pour déterminer le marquage de la position de départ. De nombreuses configurations ne servent à rien, soit parce qu’elles ne peuvent pas être atteintes à partir de la configuration initiale du jeu, soit parce que la stratégie optimale trouvée les évitera. Les petits ronds représentent les positions utilisant plus de 10 pièces dont le marquage a été calculé et mémorisé pour arriver au marquage de la position initiale.
Pour contrôler que la stratégie est optimale, il suffit de s’assurer que (a) de toute position marquée gagnante pour le joueur A, on peut atteindre une position marquée perdante pour le joueur B et que (b) tous les coups permis par les règles à partir d’une position marquée perdante pour le joueur B conduisent à des positions marquées gagnantes pour le joueur A. La possibilité de parties nulles complique un peu l’idée, mais le principe reste le même.
Dans le cas du jeu de Dames anglaises, l’analyse rétrograde n’est pas praticable sur la totalité des configurations, car leur nombre, 5×1020, est trop grand. Cependant, même partiel, ce marquage par l’analyse rétrograde est utile. Dès les premières versions de Chinook, de tels marquages étaient faits à l’avance et utilisés par le programme qui, grâce à cela, ne commettait aucune erreur en fin de partie ; cette méthode de calcul préalable par analyse rétrograde est classique dans la programmation de tous les jeux de tableau (Échecs, Othello, etc.), où elle règle à l’avance les fins de parties, calculées une fois pour toutes.
En 1989, toutes les configurations ayant moins de quatre pièces du jeu de Dames anglaises étaient ainsi marquées et stockées. En 1994, pour le second tournoi contre Tinsley, une proportion importante des configurations à huit pièces ou moins avait été marquée. En 1996, la base de données des marquages de toutes les configurations à huit pièces ou moins était achevée et utilisée par le programme Chinook. C’était malheureusement encore insuffisant pour obtenir une stratégie parfaite. Aussi, en 2001, l’équipe entreprit de calculer le marquage par analyse rétrograde de toutes les configurations ayant dix pièces ou moins. Le travail ne fut achevé qu’en 2005, après des milliers d’heures de calculs opérées simultanément sur plusieurs dizaines de machines. Ce travail nécessita la mise au point de programmes massivement parallèles, domaine de recherche auquel l’équipe canadienne apporta des contributions intéressantes.
La base de données obtenue contient 39 000 milliards de configurations. La manipulation de cette base exige des techniques spécifiques de compression de données qui réduisent sa taille à 237 gigaoctets. Pour utiliser la base, des opérations de décompression sont donc nécessaires et ont été conçues et optimisées par les chercheurs canadiens. C’est une technologie adaptée et extrêmement délicate qui a ainsi été élaborée et appliquée pour le calcul, le contrôle et l’exploitation du marquage des configurations finales.
Après le bas, le haut
L’impossibilité d’utiliser la méthode rétrograde jusqu’à la position de départ pour obtenir une stratégie optimale de jeu a alors contraint les chercheurs à attaquer le problème par l’autre bout : le début de la partie.
À la méthode rétrograde et aux bases de données qu’elle produit, on a donc adjoint une méthode nouvelle « en avant », qui oriente le marquage vers des parties de l’espace des configurations et évite au calcul de s’égarer dans des recherches désespérées. Le but est toujours de découvrir une partie de l’arbre de toutes les configurations ne comportant que des positions dont le marquage a été calculé, le tout définissant une stratégie optimale.
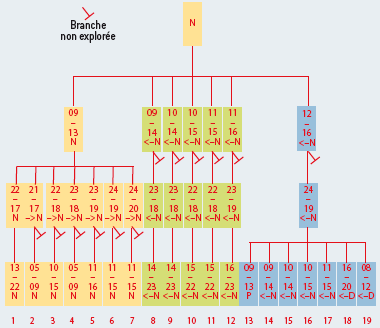
Le haut de l’arbre.
Pour déterminer le marquage de la position initiale du jeu de Dames anglaises, une partie de l’arbre des configurations a été marquée. Voici le haut de cet arbre.
Le marquage utilisé est légèrement différent de celui décrit dans l’encart 3 (analyse rétrograde), car un marquage un peu moins précis est suffisant (ce qui économise du calcul). On suppose que les deux joueurs jouent parfaitement. La lettre N indique (comme précédemment) que la partie sera nulle. Le marquage <– N signifie que la partie sera nulle ou perdue pour les Noirs, le marquage –> N que la partie sera nulle ou gagnée pour les Noirs et le marquage P que la partie sera perdue pour les Noirs. Les déplacements des pions suivent la numérotation des cases de la figure b dans l’encart 1 (règles).
Les branches non explorées représentent des coups possibles qu’il n’est pas nécessaire d’explorer pour conclure sur la nature de la position de départ (comme expliqué dans l’exemple avec la pile de pions de l’encart 1).
Notons que pour prouver qu’une configuration donnée est perdante, gagnante ou nulle, il est inutile de marquer toutes les configurations ; seules celles susceptibles d’être atteintes selon les règles du jeu importent. Dans la méthode « en avant », on ne cherche pas à marquer toutes les configurations, mais uniquement celles d’une partie de l’arbre du jeu, que la stratégie optimale exploitera en forçant l’adversaire à ne pas la quitter. Précisément, dans le cas du jeu de Dames anglaises, l’arbre partiel finalement marqué et stocké par l’équipe canadienne comporte 107 configurations, nombre 10 000 milliards de fois plus petit que le nombre de configurations total.
Voici l’idée utilisée pour cette recherche « en avant » d’une stratégie optimale. Un programme nommé contrôleur tente, à partir de la situation de départ, d’engendrer progressivement l’arbre prouvant que cette situation initiale du jeu est gagnante, perdante ou nulle. Le contrôleur détermine à chaque étape quelles sont les positions qui méritent d’être évaluées (c’est-à-dire dont il peut être intéressant de trouver le marquage exact), et il lance sur ces configurations soigneusement sélectionnées des programmes nommés résolveurs, qui tentent de découvrir le marquage.
Les algorithmes écrits pour le fonctionnement du contrôleur s’appuient sur des méthodes heuristiques, c’est-à-dire sur des méthodes qui évaluent sans certitude absolue qu’il est utile de s’attaquer à telle configuration ou à telle autre, et qui organisent les traitements prioritaires. Toutefois, l’usage de ces méthodes heuristiques n’a pas d’effet sur la certitude du résultat final. Les méthodes heuristiques guident le calcul de la recherche d’un arbre prouvant le marquage de la position de départ et, une fois trouvé, ce marquage est vérifiable sans avoir à utiliser d’heuristiques. Si les heuristiques sont bonnes, une stratégie optimale est trouvée plus rapidement que si elles sont mauvaises, mais ce qui est éventuellement trouvé au bout du compte est un arbre définissant, sans aucun risque d’erreurs, une stratégie optimale.
Les résolveurs utilisés dans cette recherche ont été de deux types, et là encore leur agencement réciproque est subtil. Le premier type de résolveur est construit sur une ancienne version du programme Chinook. Normalement, Chinook exploite des méthodes heuristiques ne permettant pas le marquage sans erreur des configurations qu’on lui soumet. Cependant, dans certains cas, le résultat proposé est rendu sûr et donne donc un marquage garanti. Lorsque ce n’est pas le cas, les informations calculées par l’ancien Chinook sont quand même utiles et transmises au programme contrôleur qui les exploite pour reconsidérer l’ensemble des configurations à traiter et leur ordre. Lorsque le premier résolveur ne donne pas d’informations assez précises, un second résolveur, fondé sur des travaux de recherche de Ayumu Nagai, de l’Université de Tokyo, est mis au travail. L’ensemble des sous-problèmes à résoudre évolue ainsi petit à petit, géré globalement par le contrôleur qui coordonne les tâches confiées aux résolveurs et récupère auprès d’eux des informations pour la construction de la stratégie optimale.
Pour que le calcul aboutisse plus vite, une méthode d’approximations successives a aussi été mise en œuvre dans l’organisation générale du calcul. Dans un premier temps, on ne recherche pas un arbre dont chaque marquage est certain, on se contente de marquages approchés : la stratégie optimale trouvée ainsi n’est pas absolument garantie, même si c’est sans doute une assez bonne méthode de jeu. Elle sert de guide pour organiser une seconde étape de calcul qui produit de nouveaux marquages plus sûrs. De proche en proche, l’erreur due aux marquages approchés est réduite, et, au bout du calcul, le contrôleur dispose de marquages parfaits et donc d’une stratégie optimale valide.
Le calcul qui a abouti en avril 2007 s’est déroulé pendant plusieurs mois ; il était distribué entre une cinquantaine de machines calculant simultanément les explorations nécessaires. L’arbre trouvé permet un jeu parfait et peut être consulté sur le site.
La méthode ressemble à celle utilisée lorsque l’on résout un Sudoku. Beaucoup de travail et de raisonnements utilisant toutes sortes d’astuces, voire d’intuitions et même de prises de risques, sont nécessaires pour trouver la solution. Cependant, une fois celle-ci obtenue, la vérification qu’elle est exacte consiste simplement en un contrôle mécanique du tableau, ce qui ne demande plus aucun raisonnement et ne repose donc plus sur les méthodes peut-être imparfaites utilisées dans la phase de découverte.
La méthode est finalement un mélange entre :
- d’une part, un calcul fait à l’avance, le marquage de toutes les configurations ayant dix pièces ou moins, dont les résultats sont stockés en utilisant de grandes quantités de mémoire et des techniques de compressions de données ;
- et d’autre part, un autre calcul prolongé « en avant » monopolisant des dizaines d’ordinateurs pendant des mois, coordonnés par un contrôleur et qui, pour aboutir rapidement, n’hésite pas à utiliser toutes sortes d’approximations et de raisonnements heuristiques.
En théorie, une méthode uniquement fondée sur la mémoire est possible : la méthode rétrograde de marquage des 5×1020 configurations du jeu. En théorie aussi, une méthode « en avant » uniquement fondée sur des calculs prolongés d’un algorithme classique (nommé minimax sans limitation de profondeur) aurait aussi conduit à une stratégie parfaite. Cependant, l’état des technologies disponibles rend inutilisables les deux méthodes « pures » utilisées seules. C’est finalement une très délicate et complexe association des deux qu’il a fallu inventer et faire fonctionner.
Un théorème démontré par la machine
La découverte d’une stratégie optimale établissant que la position de départ du jeu de Dames anglaises conduit à une partie nulle en présence de deux joueurs parfaits est un travail de démonstration automatique. En effet, au bout du compte, on dispose d’un théorème nouveau « la position de départ du jeu de Dames anglaises est de type nulle » et d’une démonstration de ce résultat, car l’arbre marqué trouvé par le contrôleur contient tous les éléments nécessaires à une preuve du théorème – preuve qui peut donc être vérifiée indépendamment (ce qui a d’ailleurs été entrepris). Par rapport aux grandes démonstrations utilisant des ordinateurs – par exemple, pour le théorème des quatre couleurs ou la conjecture de Kepler –, il faut noter une double nouveauté :
- jamais la recherche d’une démonstration n’a nécessité un aussi long et complexe calcul s’étalant sur de nombreuses années et s’appuyant sur des technologies informatiques aussi variées ;
- jamais l’utilisation d’heuristiques n’a été aussi essentielle dans la recherche d’une preuve. Ces heuristiques, qui doivent être vues comme des conseils intelligents donnés par l’homme pour guider le calcul de la machine, sont le plus souvent absentes des méthodes de démonstration automatique (ou y jouent un rôle secondaire) ; ici, sans elles, rien n’aurait été possible.
L’intelligence du jeu, acquise par les joueurs du jeu de Dames anglaises et traduite dans les heuristiques utilisées à plusieurs niveaux dans les programmes des chercheurs canadiens, et l’intelligence humaine travaillant des années à l’élaboration de nouvelles méthodes et coordonnant une multitude de techniques informatiques ont permis un calcul qui, grâce au niveau actuel de notre technologie (aussi bien concernant le stockage des données, que le calcul rapide), a produit la démonstration d’un résultat mathématique d’énoncé simple. Le résultat de l’équipe canadienne n’est pas une victoire de la machine sur l’homme, mais une victoire de l’homme lui-même : celui-ci, par la maîtrise d’outils de calculs et de stockage qu’il a construits, obtient ce qu’aucun humain seul n’obtiendrait seul, et ce qu’aucune machine programmée naïvement ne pourra jamais obtenir non plus. Tinsley était sans doute un génie du jeu de Dames, le nouveau Chinook, grâce au travail de l’équipe de J. Schaeffer, égale et dépasse l’imbattable maître, et cette affirmation est un théorème mathématique.
L’avenir et les autres jeux
Quel est l’avenir des jeux de cette catégorie ? D’abord le problème du jeu de Dames anglaises n’est pas totalement réglé : une stratégie optimale n’est pas connue pour toutes les positions possibles des pièces (alors que c’est le cas pour le jeu Awari), mais seulement pour la position standard de début de partie. Cette nuance n’est pas sans importance, car dans de nombreux tournois entre joueurs humains, les parties ne commencent pas de la position de départ standard, mais d’une position tirée au hasard en faisant faire trois mouvements licites aux pièces. Pour devenir invincible lors de ces compétitions, il faudrait déterminer les stratégies optimales d’environ 200 positions, ce qui, d’après J. Schaeffer, pourrait exiger une autre décennie de travail !
Le jeu de Dames français (aussi nommé jeu de Dames international), qui se joue sur un damier 10×10, est nettement plus difficile que la version anglaise et il ne semble pas concevable que, dans un avenir immédiat, un résultat équivalent à celui des Canadiens soit atteint.
Le nombre de configurations possibles au jeu d’échecs est environ le carré du nombre de configurations possibles au jeu de Dames anglaises. Cela permet d’affirmer que la mise au point d’une stratégie optimale pour les échecs restera impossible durant de nombreuses décennies encore. Pour ce jeu, même si l’ordinateur gagne aujourd’hui, l’espoir qu’un humain puisse renverser les choses persistera longtemps. Quant au jeu de Go, malgré de récents progrès dans sa programmation, il n’est même pas question d’amener les ordinateurs à jouer au niveau des champions.
- Chinook : information détaillée proposée par l’équipe des chercheurs de l’Université d’Alberta et possibilité de jouer avec Chinook sur le site.
- S. Gelly, R. Munos, L’ordinateur champion de go ?, in Pour la Science, n° 354, avril 2007.
- J. Schaeffer, N. Burch, Y. Björnsson, A. Kishimoto, M. Müller, R. Lake, P. Lu, et S. Sutphen, in Science, n°317, pp.1518-1522, 14 septembre 2007 ; publication en ligne le 18 juillet 2007.
- J. Schaeffer, Y. Björnsson, N. Burch, A. Kishimoto, M. Müller, R. Lake, P. Lu, et S. Sutphen, Solving Checkers, International Joint Conference on Artificial Intelligence, pp. 292-297, 2005.
- N. Guibert, La programmation des jeux de stratégie, Pour la Science, n° 293, pp. 62-68, mars 2002.
- J. Schaeffer. One Jump Ahead, Challenging Human Supremacy in Checkers, Springer, New York, 1997.
Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°363, en janvier 2008.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).