La forme idéale d’une aile

Forme d’aile et aérodynamisme

Examinons tout d’abord quel est le rôle d’une aile, pour bien comprendre les enjeux liés à sa conception. Globalement, un avion est soumis à quatre forces principales (voir figure 1 ci-dessous) :

• le poids, qui l’attire vers le sol ;
• la portance, force générée par les ailes et s’opposant au poids ;
• la poussée provenant des réacteurs permettant l’avancée de l’avion ;
• et la traînée, force de résistance de l’air freinant l’appareil.

En régime de croisière, ces forces s’équilibrent parfaitement, tandis qu’en phase de manœuvre (décollage, virage, etc.), c’est le déséquilibre de ces forces qui permet à l’avion de changer sa trajectoire. Le rôle des ailes d’un avion est donc de générer suffisamment de portance pour compenser le poids de l’appareil. Mais, en même temps, l’aile doit produire une traînée le plus faible possible. En effet, plus la résistance de l’air est forte, plus l’avion a besoin de poussée pour conserver sa vitesse et plus il consomme d’énergie en rejetant des déchets polluants. La conception d’ailes à faible traînée et forte portance est donc un enjeu important pour l’industrie aéronautique.

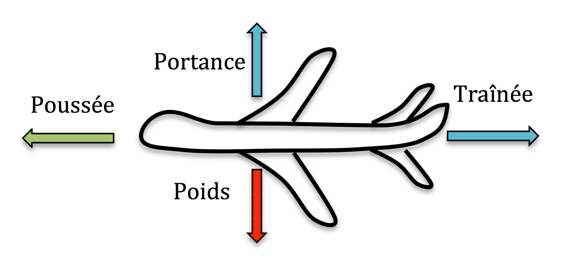
Figure 1 : forces exercées sur un avion.
Forces aérodynamiques en bleu, poussée motrice en vert, poids en rouge.

Simuler pour analyser

Comment analyser le lien entre la forme d’une aile et sa performance aérodynamique, en termes de portance et traînée ? Une première approche possible est de recourir à l’expérience et de réaliser des mesures. Cette voie a été suivie pendant des décennies, à l’aide de souffleries expérimentales, et a permis de construire les premiers avions de l’histoire, par une suite d’essais et erreurs. Cette approche est cependant très coûteuse en temps et en argent, car chaque nouvelle forme d’aile à tester nécessite la construction d’une maquette et une campagne expérimentale. L’approche alternative repose sur une analyse théorique de l’écoulement de l’air autour de l’aile. En effet, si on en connait les caractéristiques, le calcul des forces de portance et traînée est aisé. Or, on connaît depuis le milieu du 19^e siècle les équations mathématiques qui décrivent le mouvement de l’air. Il s’agit des équations de Navier-Stokes qui traduisent les principes physiques de conservation de la masse, de la quantité de mouvement et de l’énergie, dans le contexte des fluides. C’est un système de cinq équations aux dérivées partielles : cela signifie que ce sont des relations entre les variations spatiales et temporelles des grandeurs physiques de l’écoulement (densité, pression, vitesse) en tout point de l’espace et du temps. Malheureusement, on ne sait pas résoudre ces équations, à l’exception de quelques cas extrêmement simples. Jusqu’à la fin du 20^e siècle, cette approche a donc été peu fructueuse pour les problèmes pratiques. Mais l’arrivée des ordinateurs a radicalement changé cette situation.

L’accroissement de la puissance de calcul permet en effet depuis quelques années d’approcher la solution des équations de Navier-Stokes de manière précise, à défaut de pouvoir déterminer la solution exacte. La mise en œuvre de cette méthodologie peut être complexe, mais le principe est relativement simple : on commence par découper le domaine autour de l’aile en petites zones, appelées cellules de contrôle, l’ensemble étant dénommé maillage. Typiquement, un maillage peut compter plusieurs millions de cellules de contrôle. La figure 2 ci-dessous montre un tel maillage autour d’un profil (vue de l’aile en coupe verticale). On remarque que les cellules sont d’autant plus petites qu’on se rapproche de l’aile, car les phénomènes physiques y sont plus intenses et nécessitent une résolution plus fine.

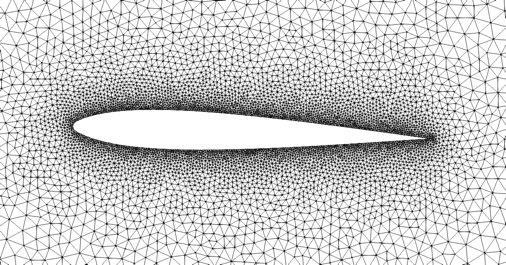
Figure 2 : Maillage autour d’un profil d’aile.

Ensuite, on suppose que les grandeurs physiques sont constantes dans chaque cellule de contrôle du maillage. À l’aide des équations de Navier-Stokes, on peut alors écrire un système d’équations reliant les grandeurs des cellules voisines. Ainsi, on contourne la difficulté mathématique en cherchant à connaître les grandeurs physiques en un certain nombre de cellules, plutôt qu’en tout point de l’espace. Plus le nombre de cellules est élevé, plus l’approximation de la solution sera précise. Par cette approche, on remplace un système de cinq équations aux dérivées partielles qu’on ne sait pas résoudre par un très grand nombre (plusieurs millions) d’équations plus simples, que l’on sait résoudre. Bien évidemment, une résolution à la main d’un si grand nombre d’équations prendrait des années à une armée d’ingénieurs ! Mais l’émergence de l’informatique a changé la donne : en traduisant les algorithmes de résolution de ces équations en programme informatique, on peut aujourd’hui calculer une solution approchée en un temps raisonnable. Cela reste cependant une approche coûteuse en temps de calcul, car une simulation peut prendre plusieurs heures à un super-ordinateur constitué de plusieurs centaines de processeurs. L’accélération de ces calculs est toujours à l’heure actuelle un enjeu de recherche, mêlant mathématiques (pour améliorer les algorithmes de résolution) et informatique (pour pouvoir utiliser efficacement des ressources de calcul croissantes).

À la recherche de la forme optimale

Résumons la situation : à partir des principes de conservation de la physique, on sait écrire les équations décrivant le mouvement de l’air, puis on simplifie ces équations de manière à pouvoir programmer un ordinateur pour obtenir une solution approchée. À partir de là, on peut facilement analyser la performance d’une forme d’aile donnée (portance et traînée). Trouver la forme d’aile idéale semble maintenant à portée de main : il suffit de faire varier les paramètres décrivant la forme de l’aile (envergure, angle de flèche, corde, épaisseur, incidence, etc.), comme illustrés sur la figure 3 ci-dessous, et de retenir la forme qui minimise la traînée, pour une portance imposée égale au poids de l’avion. Ainsi, on aura déterminé la forme d’aile idéale, permettant de faire voler l’appareil en consommant le moins d’énergie possible. Malheureusement, un calcul simple permet de montrer que cette approche naïve est impossible. Supposons que seuls les cinq paramètres mentionnés ci-dessus soient pris en compte (en réalité, il en faut beaucoup plus pour définir une aile). Si on teste seulement 10 valeurs pour chaque paramètre (ce qui est faible), il faudrait simuler 10⁵ configurations, soit réaliser 100 000 simulations. Si on suppose que chaque simulation dure par exemple 10 heures, il faudrait au total 114 années de calcul ! Même si la puissance de calcul des ordinateurs croît chaque année, cette approche systématique restera encore pour longtemps impossible.

Figure 3 : paramètres décrivant globalement une forme d’aile.

Il va donc falloir éviter de simuler toutes les configurations possibles systématiquement. Pour cela, on a recours à un algorithme d’optimisation, qui va choisir judicieusement les simulations à réaliser pour maximiser la performance. L’approche la plus classique repose sur le concept d’analyse de sensibilité, consistant à se poser la question suivante : étant donnée une forme d’aile, comment se modifient l’écoulement et la performance aérodynamique, si l’on perturbe de manière infinitésimale cette forme ? Cette question peut être formalisée de manière mathématique, en propageant une perturbation dans les équations de Navier-Stokes. Après quelques calculs, on aboutit ainsi à un nouveau système d’équations qui peut être résolu de manière analogue aux équations de l’écoulement. En inversant cette analyse — on parle alors de méthode adjointe, on peut calculer la perturbation infinitésimale de forme à appliquer pour obtenir une amélioration maximale de la performance. L’algorithme à mettre en œuvre se définit alors facilement : à partir d’une forme d’aile initiale, on simule l’écoulement, puis on réalise une analyse de sensibilité qui fournit une perturbation de forme. En appliquant cette perturbation avec une certaine amplitude, déterminée par des essais successifs, on obtient une nouvelle forme d’aile, meilleure que la précédente. Ce processus peut se poursuivre, ce qui définit une suite de formes d’aile dont la performance croît progressivement jusqu’à obtenir une forme optimale. Ce terme signifie qu’aucune amélioration de la performance ne peut plus être obtenue par perturbation infinitésimale de la forme. En pratique, ce processus itératif est stoppé dès que l’amélioration de la performance devient négligeable. Un tel exercice d’optimisation requiert typiquement quelques dizaines de simulations pour atteindre une forme optimale, ce qui reste coûteux du point de vue du temps de calcul, mais acceptable dans le contexte de la conception d’un avion qui a une durée de vie de plusieurs dizaines d’années. La figure 4 ci-dessous montre le résultat d’une optimisation de la forme d’un profil d’aile et compare les champs de pression autour du profil initial et optimal. Dans ce cas, on ne considère pas les paramètres définissant la forme globale d’une aile (cf. figure 3), mais on optimise la position de 10 points de contrôle, qui permettent de définir très précisément les courbes formant les parties supérieure et inférieure du profil. On remarque que la différence entre les deux formes est très légère, principalement concentrée sur l’avant du profil (plus fin pour la forme optimale) et le milieu de la courbe supérieure (bombée pour la forme optimale).

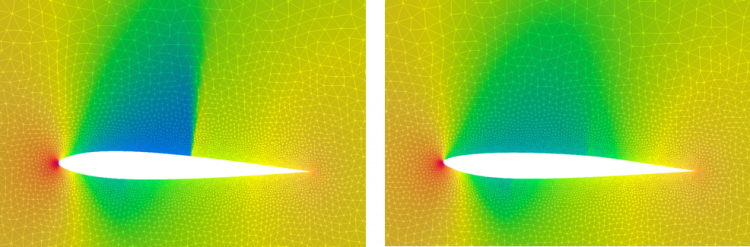
Figure 4 : simulation du champ de pression autour d’un profil d’aile (les zones bleues correspondent à des pressions basses, les rouges à des pressions élevées). À gauche, le profil initial, à droite le profil optimal. On remarque la zone en bleu au dessus du profil, représentant une zone de basse pression qui « aspire » l’aile vers le haut. Pour le profil initial, on note la présence d’un retour soudain à une pression plus forte. Il s’agit d’un phénomène d’onde de choc générant beaucoup de traînée. Pour le profil optimal, l’algorithme d’optimisation a déterminé une modification très légère de la forme permettant d’amoindrir significativement ce phénomène. Ces deux profils génèrent la même portance, mais le profil optimal réduit la traînée de pression d’environ 50 %.

Une forme idéale ?

La méthodologie décrite précédemment nous permet donc de déterminer une forme d’aile optimale, en combinant des principes physiques, analyse mathématique, algorithmes numériques et mise en œuvre informatique. A-t-on pour autant défini la forme d’aile idéale qui doit équiper tous les avions ? La réponse est malheureusement négative, et ce pour diverses raisons. Tout d’abord, la méthode d’optimisation proposée nous fournit une suite de formes d’aile, à partir d’une forme initiale, jusqu’à une forme optimale. Mais est-on sûr d’obtenir la même forme finale en partant d’une forme initiale différente ? En mathématique, cette question se rapporte au concept d’unicité de la solution. Les équations de Navier-Stokes sont non linéaires, ce qui signifie que les effets ne sont pas proportionnels aux causes qui les provoquent. Une conséquence importante est qu’un problème d’optimisation de forme tel qu’évoqué ici peut présenter plusieurs configurations pour lesquelles la performance est optimale. Ainsi, suivant la forme de départ, l’algorithme d’optimisation nous conduit à l’une ou à l’autre de ces configurations. La forme optimale obtenue par un tel procédé doit donc être analysée a posteriori avec précaution. Une seconde raison est liée au fait que la recherche de la forme optimale est conduite pour des conditions de fonctionnement fixées, comme par exemple la vitesse de l’avion, son altitude, etc. La forme optimale dépend de ces paramètres et, par la suite, à chaque type d’avion et de vol va correspondre une forme optimale. Cela explique notamment la forme particulière des ailes des avions supersoniques, comme le Concorde, caractérisé par sa voilure triangulaire. Enfin, la recherche de la forme optimale dans la construction aéronautique nécessite de prendre en compte un certain nombre de contraintes. Par exemple, il faut que la forme d’aile optimale soit constructible, qu’elle soit le moins lourde possible, ou encore que sa structure supporte les déformations et vibrations engendrées par les conditions de vol. Avec les progrès de l’ingénierie mécanique et des matériaux, ces contraintes évoluent et donc la forme d’aile optimale aussi. Ces progrès technologiques expliquent pourquoi la forme des avions est en constante évolution.

Dans le contexte actuel, marqué par la nécessité de réduire l’impact environnemental du transport aérien tout en faisant face à l’augmentation du trafic, l’industrie aéronautique doit pourtant faire plus qu’optimiser progressivement la performance aérodynamique des avions. Des concepts futuristes émergent ainsi des laboratoires de recherche, souvent inspirés de la nature, comme l’utilisation d’ailes déformables s’adaptant aux fluctuations des écoulements d’air ou encore des surfaces équipées d’obstacles micrométriques pour réduire les frottements. La conception optimale de ces nouveaux dispositifs est difficile, car elle nécessite une analyse multidisciplinaire et multiéchelle, mêlant aérodynamique, structure, matériau, et la prise en compte de critères d’optimisation multiples liés à l’ensemble de ces disciplines. Les méthodes d’optimisation classiques, comme celle présentée dans cet article, sont peu adaptées à cette problématique. Pour relever ce défi de conception, élément clé du transport aérien de demain, de nouvelles stratégies combinant mathématiques et informatique sont donc à inventer, s’appuyant par exemple sur les progrès actuels en intelligence artificielle pour analyser l’influence des paramètres de conceptions, aux différentes échelles incriminées, sur les phénomènes physiques en jeu.