La mécanique quantique comme garant de sécurité pour l’échange de clé secrète

Pour qu’Alice et Bob puissent s’envoyer des données de façon confidentielle, il faut qu’ils aient une clé secrète. Cette clé secrète peut être générée par un protocole quantique d’échange de clé comme l’ont montré Bennett et Brassard en 1984. Dans ce protocole quantique, Alice et Bob utilisent chacun un dispositif quantique qui leur permet d’encoder l’information qui est transmise entre eux. La sécurité de ce protocole est garantie par une preuve mathématique, mais afin d’utiliser cette preuve en pratique, il faut que les dispositifs quantiques soient implémentés comme le modèle mathématique l’exige. En effet, un défaut d’implémentation peut rendre le protocole vulnérable à une attaque non prise en compte par le modèle. De tels défauts peuvent être involontaires (bruit, négligence, …) mais aussi conçus intentionnellement par un adversaire ayant eu accès au dispositif (par exemple le constructeur, vendeur, …). Comment s’assurer que le protocole, même s’il n’est pas implémenté parfaitement, reste sûr ? Est-il possible de garantir la sécurité d’un protocole sans connaître les détails de l’implémentation des dispositifs utilisés ? Étonnamment, la réponse est oui grâce à une propriété de la mécanique quantique. Ainsi, à condition que les dispositifs soient bien isolés, on obtient alors un protocole dit « device-independent », c’est-à-dire dont la sécurité ne dépend pas des détails d’implémentation des dispositifs utilisés.

Jeu collaboratif à deux joueurs

La brique de base dans les protocoles « device-independent »» est un jeu collaboratif à deux joueurs (Alice et Bob) avec un arbitre. Détaillons tout d’abord un tel jeu, avant de montrer son utilisation dans le protocole d’échange de clés secrètes. Avant la partie, Alice et Bob peuvent décider d’une stratégie commune qui dépend des règles du jeu que l’on décrira plus tard. Dès que la partie commence, Alice et Bob ne peuvent plus communiquer et l’arbitre choisit une question \( x \in \{ 0,1\}\) au hasard qu’il envoie à Alice et une autre question \( y \in \{ 0,1\}\) au hasard qu’il envoie à Bob. Chacun des joueurs renvoie à l’arbitre une réponse (\(a\) pour Alice et \(b\) pour Bob) comme indiqué dans la Figure 1. L’arbitre, ayant accès aux questions et aux réponses décide alors si les joueurs ont gagné ou perdu la partie en fonction des règles du jeu décrite dans le Tableau 1.

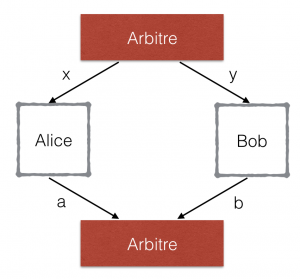
Figure 1 – Le déroulement d’une partie du jeu.

Par exemple, d’après la première ligne du tableau, lorsque Alice reçoit \(x=0\) et Bob reçoit \(y=0\) alors les réponses (\(a=0\), \(b=0\)) et (\(a=1\), \(b=1\)) sont gagnantes alors que (\(a=0\), \(b=1\)) et (\(a=1\), \(b=0\)) sont perdantes. On peut résumer la condition de gain par la formule suivante : \(x \wedge y = a \oplus b\) où \(\wedge\) représente le « et » logique et \(\oplus\) le « ou exclusif ».

Pour le jeu décrit dans le tableau, Alice et Bob peuvent choisir la stratégie qui est de renvoyer la valeur \(0\) quelle que soit la question. Avec cette stratégie, ils gagnent dans tous les cas sauf lorsque \(x=y=1\), c’est-à-dire avec une probabilité de 0.75. Mais peuvent-ils faire mieux ? Il faut bien garder en tête qu’Alice et Bob ne peuvent pas communiquer après avoir reçu leurs questions et donc Bob ne connaît pas la valeur de \(x\). Ainsi, lorsqu’il reçoit la question \(y=1\), il ne sait pas si Alice a reçu \(x=0\) auquel cas il faut satisfaire \(a=b\) pour gagner ou bien si \(x=1\) auquel cas, au contraire la condition pour gagner est \(a \neq b\). Il est assez facile de se convaincre que ce n’est pas possible de gagner à ce jeu avec une probabilité supérieure à 0.75. En effet, si on note \(A_0\) et \(A_1\) les réponses d’Alice lorsqu’elle reçoit respectivement \(x=0\) et \(x=1\), et \(B_0\) et \(B_1\) les réponses de Bob lorsqu’il reçoit respectivement \(y=0\) et \(y=1\), il suffit d’observer que pour tous les choix possibles de \(A_0\), \(A_1\), \(B_0\), \(B_1\) (toutes les stratégies déterministes possibles), au plus trois des quatre conditions du Tableau 1 sont satisfaites.

Que se passe-t-il si Alice et Bob sont autorisés à utiliser les lois de la mécanique quantique ? Dans ce cas, Alice et Bob ont chacun une particule quantique (par exemple un photon) et vont se mettre d’accord sur une stratégie quantique. Une stratégie quantique pour Alice est définie mathématiquement par deux bases orthonormées du plan : \( ( \vec{A_0}(0), \vec{A_0}(1))\) pour l’entrée \(x=0\) et \( ( \vec{A_1}(0), \vec{A_1}(1) ) \) pour \(x=1\). Et de même pour Bob, sa stratégie est définie par deux bases orthonormées \( ( \vec{B_0}(0), \vec{B_0}(1) )\) et \( ( \vec{B_1}(0), \vec{B_1}(1) ) \). Étant donnée une telle stratégie, Alice et Bob jouent au jeu de la façon suivante. Lorsqu’elle reçoit la question \(x\), Alice « mesure » sa particule dans la base \( ( \vec{A_x}(0), \vec{A_x}(1) )\) et obtient un résultat \(a \in \{ 0,1\} \) qui correspond à sa réponse. Dans le cas d’un photon, cette mesure correspond à utiliser un polariseur aligné avec la base \( ( \vec{A_x}(0), \vec{A_x}(1) )\) et la réponse est \(a=0\) si le photon passe et \(a=1\) si le photon est bloqué. Bob utilise la même procédure, mais sur sa particule et en utilisant la base \( ( \vec{B_y}(0), \vec{B_y}(1))\) s’il reçoit la question \(y\).

La découverte très surprenante du physicien John Bell est que si les particules d’Alice et Bob sont préparées dans un état quantique particulier, dit état intriqué, alors ils peuvent gagner à ce jeu avec une probabilité \( \cos ^2 \left( \frac{\pi}{8} \right) \approx 0.85 > 0.75\). On dit que l’état de deux particules quantiques est intriqué lorsque les deux particules ont une forme de corrélation forte permise par les lois de la mécanique quantique. La nature étrange de l’intrication avait été réalisée par Einstein, Podolsky et Rosen dès les années 1935, mais c’est John Bell en 1964 qui a exploité ce phénomène de manière précise à travers un tel jeu.

Si les particules d’Alice et de Bob sont préparées suivant le bon état intriqué, alors on obtient les probabilités suivantes pour une stratégie donnée. Pour les questions \(x\) et \(y\), la probabilité d’obtenir les réponses \(a\) et \(b\) est donnée par \( \frac{1}{2} \left| \langle \vec{A_x}(a) | \vec{B_y}(b) \rangle \right| ^2\). Prenons d’abord un exemple simple : si les 4 bases définissant les deux stratégies sont les mêmes, alors pour tout \(x\), \(y\), on obtient toujours \(a=b\). En effet, en utilisant l’orthogonalité de la base, on a \( \langle \vec{A_x}(a)|\vec{B_y}(b) \rangle =0\) lorsque \( a \neq b\) et \( \langle \vec{A_x}(a)|\vec{B_y}(b) \rangle =1\) lorsque \(a=b\) ; comme \(a=b\) recouvre les deux cas \(a=b=0\) et \(a=b=1\) qui sont équiprobables, la probabilité d’obtenir les réponses \(a=b=0\) est \(\frac{1}{2}\) et la probabilité d’obtenir \(a=b=1\) est également \(\frac{1}{2}\). Ceci signifie que cette stratégie est gagnante dans tous les cas sauf lorsque \(x=y=1\), ce qui donne encore une probabilité de gagner de 0.75. Pour faire mieux que 0.75, il faut construire des vecteurs tels que \( \vec{A_x}(0) \) est « proche » de \( \vec{B_y}(0) \) lorsque \(x=y=0\), ou \(x=0\) et \(y=1\), ou encore \(x=1\) et \(y=0\), mais « éloigné » lorsque \(x=y=1\). La Figure 2 illustre une stratégie qui satisfait ces propriétés. On obtient pour tout \(x\), \(y\), si \(a\) et \(b\) satisfont les conditions gagnantes du Tableau 1, alors \( \left| \langle \vec{A_x}(a) | \vec{B_y}(b) \rangle \right| ^2 = \cos ^2 \left( \frac{\pi}{8} \right) \), ce qui au total donne une probabilité de gagner de \(\cos ^2 \left( \frac{\pi}{8} \right) \approx 0.85 \).

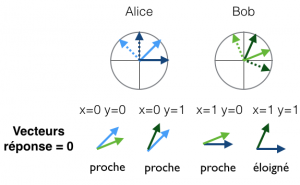
Figure 2 – Une stratégie quantique avec probabilité de gain \(\cos ^2 \left( \frac{\pi}{8} \right) \approx 0.85 \).

Les deux bases d’Alice sont représentées en bleu et celles de Bob en vert. La base en couleur claire correspond à la question \(0\) et la couleur foncée à la question \(1\). Le vecteur en continu correspond à la réponse \(0\) et le vecteur en pointillé correspond à la réponse \(1\). On dit que deux vecteurs sont « proches » lorsque le cosinus au carré de leur angle vaut \( \cos ^2 \frac{\pi}{8}\) (c’est-à-dire qu’ils forment un angle de \( \frac{\pi}{8}\) ou \(\frac{7 \pi}{8}\)) et on dit qu’ils sont « éloignés » si le cosinus au carré de leur angle vaut \( \cos ^2 \frac{3 \pi}{8} \).

Jeu collaboratif et protocole « device-independent »

Comment utiliser un tel jeu pour construire un protocole « device-independent » ? L’observation importante pour faire ce lien est de réaliser qu’un gain au jeu avec une probabilité strictement supérieure à 0.75 certifie que les dispositifs utilisés ne peuvent pas être déterministes. En effet, comme décrit précédemment, on sait que pour toute stratégie déterministe, la probabilité de gagner est bornée par 0.75. On ne peut pas a priori exactement caractériser le fonctionnement des dispositifs, mais on peut assurer que si les dispositifs sont bien isolés pendant la partie du jeu, alors les réponses \(a\) et \(b\) qui sont générées par les joueurs doivent contenir de l’aléa qui pourra être utilisé pour construire la clé secrète.

Concrètement, Alice et Bob utilisent leurs dispositifs quantiques pour jouer au jeu \(n\) fois de manière séquentielle avec les questions \(x_1, \ldots , x_n\) et \( y_1, \ldots , y_n\) qui sont générées au hasard. Alice obtient les réponses \( a_1, \ldots, a_n\) et Bob les réponses \(b_1,\ldots,b_n\). Ensuite, Alice choisit un ensemble \( T \subset \{ 1, \ldots, n\}\) au hasard et envoie \(T\), \(\{ x_i \: : \: i \in T\}\) et \( \{ a_i \: : \: i \in T \} \) à Bob. Bob compte la fraction des parties de \(T\) qui ont été gagnées :

\( \eta = \frac{| \{ i \in T \: : \: x_i \wedge y_i = a_i \oplus b_i\}|}{|T|}.\)

Si \( \eta \leq 0.75\), Bob annonce l’abandon du protocole (cela signifie que les dispositifs ne sont pas bons). Si par contre \(\eta\) > 0.75, alors Alice et Bob peuvent garantir que les séquences \( a_1, \ldots , a_n\) et \( b_1, \ldots , b_n\) contiennent de l’aléa privé. La génération de la clé secrète se fait à l’aide d’un algorithme classique (c’est-à-dire sans rien de quantique) qui utilise des techniques qui sortent du cadre de cet article (des codes correcteurs et des fonctions de hachage). Le lecteur ou la lectrice intéressé·e peut trouver des explications de cette génération dans [5,6].

À l’heure actuelle, les travaux de recherche en cryptographie quantique « device-independent » restent encore théoriques et les réalisations expérimentales se limitent à des preuves de principe. La difficulté vient du fait que même si on sait créer des états intriqués, il est important pour faire une vraie démonstration du protocole de réduire au maximum les différentes sources d’erreurs. Mais avec le développement des technologies quantiques, il ne fait nul doute que nous verrons ces protocoles d’échange de clé mis en pratique.

Références pour en savoir plus :

1. Ces deux vidéos de la chaîne YouTube « Science étonnante », de David Louapre, expliquent ce que sont les états intriqués d’une part et un jeu qui ressemble à celui présenté ici d’autre part, mais avec des gâteaux  ces vidéos accompagnent des articles de blog : L’intrication quantique (et son billet de blog associé sur l’intrication quantique ) et Le mystère des gâteaux quantiques (et son billet de blog associé sur l’expérience des gâteaux quantiques, qui ressemble au jeu décrit ici).
2. Franck Laloë, « L’argument de Einstein, Podolsky et Rosen », Bibnum [En ligne], Physique, mis en ligne le 01 octobre 2010, consulté le 11 octobre 2020.
3. Article Wikipédia sur le paradoxe Einstein, Podolsky, Rosen.
4. Ekert, A., Renner, R. The ultimate physical limits of privacy. Nature 507, 443–447 (2014).
5. Article Wikipédia sur la distribution de clé quantique (en anglais), consulté le 20 janvier 2021. Sur le même sujet, ces vidéos (en anglais) qui font partie d’un cours sur la cryptographie quantique sont d’un niveau nettement plus avancé, mais plus complet : Privacy amplification et Introduction to information reconciliation.