Le cerveau est-il un bon modèle de réseau de neurones ?
1. Question de point de vue
Au juste, que savons-nous du fonctionnement du cerveau ?
Traiter et interpréter les informations qui proviennent du monde extérieur, via les organes sensoriels, et produire, en réponse, un comportement adapté : c’est le rôle du cerveau de tous les animaux. Et pour l’espèce humaine, c’est aussi : développer des langages évolués, produire des théorèmes mathématiques, créer des œuvres d’art… Toutes ces capacités étonnantes du cerveau, force est de constater qu’on est encore bien loin de les comprendre ou de les expliquer.
Les données issues de l’imagerie contribuent à l’étude de l’activité cérébrale.
© INRIA / Photo Jim Wallace
Et pourtant, la structure du cerveau et du système nerveux en général est de mieux en mieux connue. L’acquisition de données anatomiques est continue depuis des générations, résultant par exemple d’observations d’effets post-traumatiques. De nouveaux protocoles expérimentaux et de nouvelles techniques d’imagerie sont élaborés ; les moyens de traitement informatique sont en expansion. La médecine, la biologie, la neurophysiologie se développent.
Tout cela révèle toujours plus la structure hautement complexe, différenciée et hiérarchisée du cerveau. On sait maintenant ce qui se produit dans les différentes régions du cerveau. Où précisément, par exemple, le cerveau a une activité qui correspond à la détection des contours d’une image. Cette régularité de structure a permis en particulier de mettre en évidence son aspect multi-échelles, de l’échelle des neurones à celle des réseaux de neurones, par exemple les colonnes corticales, elles-mêmes organisées en réseaux…
Décrire l’anatomie fonctionnelle du cerveau n’est pas chose facile. On observe d’abord que le cerveau est constitué de deux hémisphères, droit et gauche. On distingue ensuite des structures caractéristiques, comme le cortex, structure plissée qui couvre la surface du cerveau, ou le thalamus, structure essentielle du système nerveux central, etc.
Le cortex est composé de quatre lobes, qui sont eux-mêmes subdivisés en aires corticales. À chacune correspond une grande fonction. L’aire de Broca, par exemple, est située dans le lobe temporal (hémisphère gauche). Cette aire impliquée dans la compréhension du langage est l’une des premières à avoir été découverte.
Chaque aire est elle-même structurée selon la fonction exercée. Ainsi, les aires motrices et sensitives ont une géométrie qui correspond au corps humain, ceci au prorata de l’importance de la zone en ce qui concerne le mouvement ou la sensation. Stimuler la zone motrice déclenchera un mouvement de la partie du corps correspondante, stimuler la zone sensitive produira une impression tactile.
Si on effectue un zoom sur une partie du cortex, on découvre une autre régularité : il se présente comme une immense surface repliée. Cette surface est organisée dans sa profondeur en six couches, chaque couche ayant un rôle bien particulier. Mieux ! Elle se compose de colonnes corticales, chaque colonne étant un petit groupe de 100 à 1000 neurones dont l’activité correspond à un paramètre très précis : l’orientation d’un contour ou une couleur à un endroit de la rétine par exemple. Ces colonnes sont regroupées en cartes qui sont à la base des transformations effectuées dans le cortex.
Pour en découvrir plus sur ces aspects, nous vous recommandons l’excellent site Web Le cerveau à tous les niveaux.
La partie du cerveau correspondant à la vision est le cortex visuel. La détection des contours de l’image, de la couleur, de la profondeur, etc. s’y organisent en cartes rétinotopiques, qui reproduisent la topographie de la rétine.
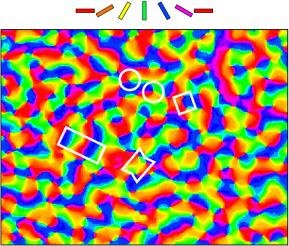
Vue d’environ 3 x 4 mm du cortex visuel primaire d’un chat.
Chaque couleur correspond à la détection d’une orientation donnée des contours de l’image observée. Chaque bloc de couleur correspond à une petite région de la rétine. Comprendre cette hyper-structure a permis de comprendre à quel paramètre du stimulus visuel correspondait l’activité du cerveau dans cette zone.
Et de cette structure, on déduit un modèle du cerveau ?
Pas si vite ! Dans les neurosciences collaborent un grand nombre de communautés, des neurophysiologistes, des biologistes, des médecins aux roboticiens, aux informaticiens, en passant par les mathématiciens et les physiciens. Et selon que l’on est biologiste, neurophysiologiste, psychologue, mathématicien ou physicien, il y a différentes façons de comprendre et d’expliquer. Les approches, les questions, et la notion même de modèle diffèrent selon les communautés. En ce sens, il n’existe pas de « bon » modèle universellement reconnu.
Nous adoptons donc ici le point de vue – subjectif et limité – d’un physicien intéressé par l’élaboration et l’analyse de modèles mathématiques de réseaux neuronaux. Ce qui n’est pas, et de loin, vous l’aurez compris, la seule façon d’étudier le cerveau.
Qu’est-ce qu’un modèle mathématique, et un « bon » modèle mathématique ?
De ce point de vue, un modèle est un jeu d’équations visant à décrire un ensemble de phénomènes, et si possible à prédire des comportements que l’on n’a pas encore observés. Une observation préalable des phénomènes réels est nécessaire avant de dégager des caractéristiques générales permettant d’établir ces équations. Suit un processus d’abstraction qui élimine en général un certain nombre de « détails » issus de ces observations pour ne garder que les éléments jugés « essentiels ». Un modèle est donc une approximation et une abstraction de la réalité. Un « bon » modèle décrit et prédit un maximum de phénomènes avec un minimum d’équations, ou une complexité minimale dans ces équations. (La situation idéale, qui porte bien son nom d’ailleurs, étant lorsqu’on peut résoudre ces équations. Notons cependant que cette résolution n’est pas forcément nécessaire pour décrire de manière satisfaisante le comportement du système d’équations.)
Envisage-t-on vraiment de mettre le cerveau en équation ?
Revenons à notre titre quelque peu provocateur. Il y a là une pointe d’humour mais aussi une mise en garde. De fait, un « bon » modèle est avant tout destiné à poser de manière précise un ensemble (limité) de questions et (éventuellement) à y répondre. Les modèles sont issus de simplifications parfois drastiques de la réalité. Néanmoins, ils nous permettent bien souvent de comprendre et d’appréhender différemment cette réalité. Certaines fois, ils nous la rendent tout simplement intelligible. Si le modèle est très performant, à la fois explicatif et prédictif, il devient une référence et la réalité est interprétée à travers son filtre. On peut alors être conduit à estimer que les « détails » que l’on a négligés dans la construction du modèle sont effectivement non pertinents, bien qu’ils soient souvent issus d’observations. Cette démarche est féconde lorsqu’elle permet de passer d’une série d’observations à une théorie ou un modèle fédérateurs. Mais elle peut également devenir trop réductrice, évacuer des détails essentiels, en oubliant qu’une théorie ou un modèle sont valides dans un certain cadre, en vertu de certaines limites. Dans le cas du cerveau, ce type de dérive peut se produire assez facilement, et il n’est pas inutile de rappeler où sont les modèles et où la référence.
L’analyse mathématique que l’on peut produire de ce qu’on appelle actuellement réseaux de neurones, représente le travail de nombreuses équipes de recherche depuis des décennies. Mais elle est loin d’une hypothétique équation du cerveau, dont l’éventuelle découverte un jour futur et l’existence même suscitent bien des interrogations. Jusqu’où les méthodes actuelles permettent-elles donc d’aller dans l’analyse mathématique de modèles de réseaux de neurones, et à quelle distance ces modèles de réseaux de neurones se situent-ils d’un « bon modèle » du cerveau ?
Insistons sur le fait que l’approche par les réseaux de neurones n’est qu’une façon d’aborder le fonctionnement du cerveau. Elle est d’une certaine façon associée à la démarche dite réductionniste que nous développons plus loin. Actuellement, on peut considérer que l’analyse mathématique de la dynamique neuronale se concentre sur trois aspects : l’étude de la dynamique de neurones isolés, ensuite l’étude de la dynamique de réseaux de neurones, sans tenir compte de la reconfiguration des connexions entre neurones au cours du temps, et enfin, en tenant compte de cette évolution au cours du temps. Dans ces trois directions, l’état de l’art de l’analyse mathématique débouche sur des questions de recherche qui demeurent ouvertes.
Mais on utilise ces réseaux de neurones pour programmer des ordinateurs !
Attention, parlons-nous bien de la même chose ? En étudiant des modèles de neurones et de réseaux de neurones, nous cherchons avant tout à faire progresser la compréhension du cerveau. Souvent simplifiés à l’extrême, des modèles de réseaux de neurones, dits formels, servent effectivement à programmer des ordinateurs. Les chercheurs qui les utilisent n’ont pas la prétention de reproduire avec exactitude le comportement de neurones réels, ils tirent parti de certaines de leurs caractéristiques. C’est pourquoi on qualifie cette branche de l’intelligence artificielle de bio-inspirée. Ainsi, des collègues de Nancy ont programmé un petit robot renifleur, qui détecte les fumées par leur odeur. Mais ceci est une autre histoire, qu’ils vous raconteront eux-mêmes bientôt.
Revenons donc à nos neurones…
2. Question d’échelle
Il y a une cinquantaine d’années, à Cambridge, en Angleterre, deux scientifiques très « british », Alan Hodgkin et Andrew Huxley, ont révolutionné le cours de l’histoire de l’exploration du fonctionnement du cerveau. Ils sont allés observer – en détail – un bout de neurone. Celui qui permet au calamar de propulser de l’eau pour avancer. Pourquoi ce neurone ? Parce qu’il est géant ! Un millimètre de diamètre, alors que les neurones de notre cerveau humain ne sont larges que de 4 à 100 micromètres. Ils ont pu alors y insérer une électrode et effectuer des mesures de l’influx nerveux. À partir de ces observations, ils ont commencé à comprendre le lien entre le fonctionnement du neurone et les phénomènes électriques et chimiques qui l’engendrent. Et ils ont écrit ce qu’ils avaient compris sous forme d’équations. Le modèle de neurone qu’ils ont ainsi constitué, connu sous le nom de modèle de Hodgkin-Huxley, leur a valu le prix Nobel, et reste encore aujourd’hui la référence en termes de modèle de neurone.
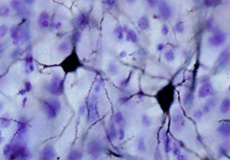
Neurones du cortex somatosensoriel d’un macaque.
Source : brainmaps.org
Depuis le début du 20e siècle, on sait que les neurones sont impliqués dans le système nerveux des différentes espèces animales, depuis des organismes élémentaires comme les vers de terre jusqu’aux espèces les plus évoluées. Ils sont en quelque sorte les « atomes » du cerveau : tout comme les atomes sont semblables dans toute la matière, les neurones des différentes espèces ont un fonctionnement comparable. Cela s’explique par la stabilité du système nerveux au cours de l’évolution. Observer et modéliser le comportement d’un neurone d’une espèce permet donc d’étudier les neurones en général.
Regardons ces coupes de cerveaux de poisson, de grenouille, d’oiseau et de primate. Comme l’a décrit Paul MacLean, on observe que les structures sont préservées au cours de l’évolution : c’est cette stabilité qui permet d’utiliser le modèle animal pour comprendre notre cerveau humain.
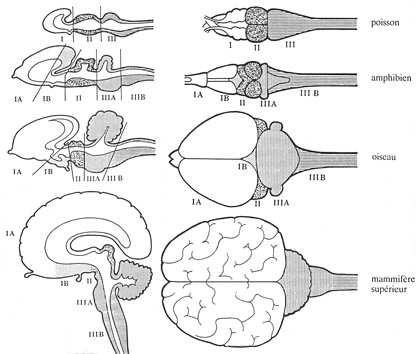
Vues comparatives du système nerveux central au cours de l’évolution.
La région IIIA, par exemple, a donné le cervelet, grâce auquel nous générons des gestes sophistiqués comme la marche. Chez l’oiseau, cette structure est superbement développée.
Notons que si chez les oiseaux le cortex est moins développé que chez les primates, leur cervelet est des plus performants, leur permettant de faire des gestes aussi extraordinaires que voler, ce qui nous sera à tout jamais interdit. Certes, nous n’avons pas de plumes, mais notre cerveau n’a pas non plus les « bons réflexes ».
Une évolution similaire de l’architecture du cerveau se produit lors de la formation de l’embryon.
Un autre exemple illustre cette stabilité neuronale. La raie a survécu lors de l’évolution des espèces en se plaquant au fond des mers pour échapper à ses prédateurs. Plutôt que d’avoir une espèce gardant toujours un de ses yeux dans le sable, l’évolution a conduit à faire émerger des poissons avec… les deux yeux sur le même côté. Pour contrôler les yeux, les mouvements du poisson sont mesurés au niveau des centres de l’équilibre près de l’oreille interne (oui, vous avez bien lu, notre oreille existe déjà chez le poisson, non pour capter les vibrations sonores, mais les vibrations de l’eau !). Évidemment, avec les deux yeux du même côté, les relations entre les mouvements du poisson et ceux des yeux changent du tout au tout. Était-il alors plus simple pour la nature de faire évoluer les paramètres du système nerveux qui contrôlent les yeux ou de bouleverser l’anatomie du crâne pour que les relations soient préservées ? La stabilité de l’architecture du cerveau veut que ce soit la deuxième option qui se soit réalisée.
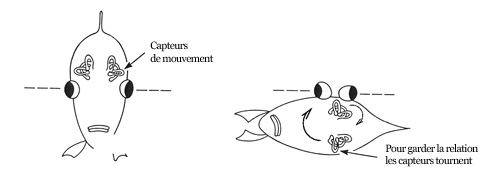
Les centres de l’équilibre du poisson suivent la position des yeux, pour que leurs relations géométriques soient préservées. Le système nerveux reste alors quasiment inchangé.
La même chose s’est produite bien plus tard dans l’évolution des espèces, quand les mammifères ont été conduits à avoir leurs yeux en position frontale (comme par exemple le chat) et non plus latérale (comme par exemple le lapin). Nous pouvons donc en conclure que le cerveau est une machinerie suffisamment complexe pour évoluer bien moins que les anatomies.
Et l’étude d’un seul neurone, que peut-elle nous apprendre sur le cerveau dans son ensemble ?
Décomposer l’objet que l’on souhaite étudier en parties élémentaires dont on va chercher à comprendre le comportement, en négligeant dans un premier temps les interactions entre les différentes parties : cette démarche scientifique, qu’on appelle l’approche réductionniste, a maintes fois fait ses preuves en physique. Et elle est pertinente aussi, jusqu’à un certain point, dans le cas du cerveau, en raison de la structure multi-échelles de celui-ci. Même si – là encore tout comme les atomes, qui ne sont pas aussi indivisibles que leur nom l’indique – les neurones ne sont pas les plus petits constituants du cerveau.
Que se passe-t-il dans un neurone ?
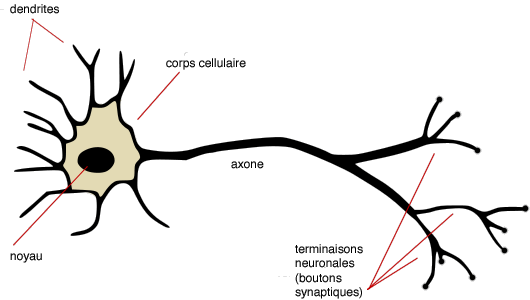
Représentation schématique d’un neurone.
Chaque neurone envoie des informations le long de son axone et en reçoit le long de ses dendrites.
Source : d’après Wikimédia
Par quels mécanismes les neurones reçoivent-ils l’influx nerveux, le transmettent-ils et surtout le transforment-ils ? Un neurone est une cellule électriquement active ; son activité se manifeste par l’émission de variations de son potentiel de membrane, on dit alors que le neurone décharge.
Les variations de potentiel émises sont appelées potentiels d’action. Dans leur modèle, Alan Hodgkin et Andrew Huxley en ont décrit l’émission et la propagation, en les reliant aux mécanismes chimiques de la cellule. L’émission dépend de l’activité conjointe d’un grand nombre de protéines de la membrane (qui à cette époque ne s’appelaient pas encore des canaux ioniques). Ces protéines, perméables aux ions sodium ou potassium, agissent comme des portes qui s’ouvrent et se ferment, faisant varier la concentration d’ions positifs à l’intérieur et à l’extérieur du neurone, donc la valeur du potentiel de membrane.
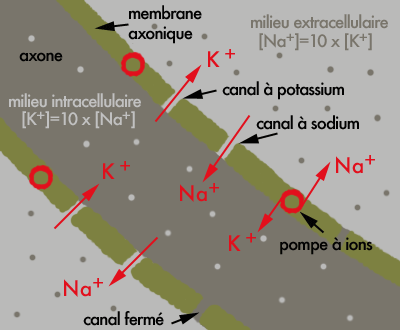
Mécanismes chimiques liés à l’activité électrique du neurone.
L’activité du neurone est contrôlée par différentes espèces d’ions, principalement sodium Na+ et potassium K+. Lorsque le neurone est au repos, la concentration en ions sodium est environ dix fois plus importante dans le milieu extérieur qu’à l’intérieur du neurone. Les ions sodium essaient donc d’entrer dans le neurone. C’est l’inverse pour les ions potassium.
Alan Hodgkin et Andrew Huxley ont décrit l’activité électrique des neurones (émission et propagation de potentiels d’action) par des équations phénoménologiques qui répondent aux lois de la physique classique (loi d’Ohm par exemple).
Dans la description faite par Alan Hodgkin et Andrew Huxley en 1952, les canaux ioniques sont constitués de portes indépendantes de trois types, qui s’ouvrent et se ferment en fonction de la valeur du potentiel de membrane. La probabilité d’ouverture de ces portes est décrite par des variables m, n et h. L’ouverture et la fermeture des portes m et h contrôlent le passage des ions sodium tandis que celles des portes n contrôlent le passage des ions potassium.
On note m la probabilité qu’une porte de type m soit ouverte (cette quantité correspond à une moyenne microscopique sur un grand nombre de canaux et sur des temps caractéristiques correspondant à un grand nombre d’ouvertures/fermetures). Cette probabilité évolue selon l’équation suivante :
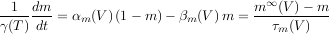
Ici, V est le potentiel de membrane ; γ(T) représente un facteur dépendant de la température ; α est une probabilité de transition ouvert/fermé et β de transition fermé/ouvert ; m∞ est la valeur asymptotique de m et τm le temps caractéristique.
De façon similaire, les équations suivantes s’appliquent pour les portes h et n :
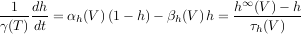
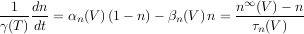
De plus, la conductivité électrique d’une portion de membrane est donnée par une fonction des probabilités d’ouverture des portes. Cette fonction a été déterminée expérimentalement par Hodgkin et Huxley. En appliquant la loi d’Ohm et la loi de Kirchoff, on obtient l’équation du potentiel de membrane :
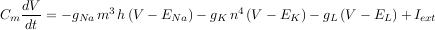
Ce système d’équations constitue le modèle local de Hodgkin-Huxley pour une portion de membrane. Le modèle spatialement étendu, qui décrit la propagation du potentiel d’action le long de l’axone, a la même structure, mais inclut un terme de couplage spatial entre portions de membrane.
Références des articles de Hodgkin et Huxley :
- A. L. Hodgkin et A. F. Huxley Current carried by sodium and potassium ions through the membran of the giant axon of Loligo. Journal of Physiology, London, 116: 449-472 (1952)
- A quantitative description of ion currents and its applications to conduction and excitation in nerve membranes. Journal of Physiology, London, 117: 500-544
Cependant, ces équations correspondent à une moyenne mésoscopique sur des phénomènes microscopiques, l’ouverture et la fermeture de « portes » dans des canaux ioniques, pour lesquels la physique classique peut ne plus être suffisante (puisqu’à cette échelle, des phénomènes quantiques apparaissent). Mais nous n’avons pas besoin d’en tenir compte ici. Nous nous focaliserons, comme Alan Hodgkin et Andrew Huxley, au niveau d’un petit morceau de membrane de neurone, mais suffisamment grand pour négliger les effets quantiques.
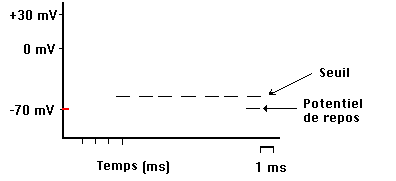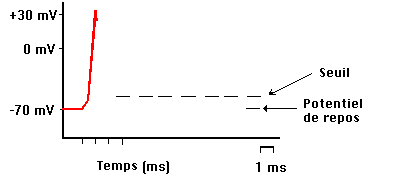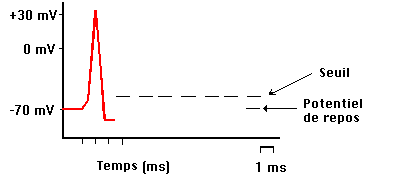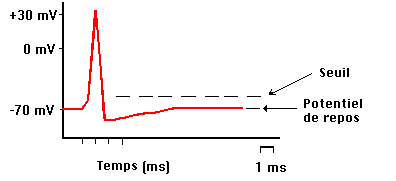
Forme d’un potentiel d’action.
Les potentiels d’action sont émis à des instants précis, par exemple lorsque le neurone est soumis à une excitation électrique suffisamment importante. La forme d’un potentiel d’action est caractéristique, une montée rapide suivie d’une descente puis d’un rebond négatif. Elle ne dépend pas de l’intensité de l’excitation émise. Les potentiels d’action se propagent le long de l’axone vers les boutons synaptiques qui assurent la communication avec d’autres neurones. Leur propagation est un mécanisme actif et non-linéaire qui permet au neurone de sélectionner une vitesse de propagation stable dépendant uniquement des caractéristiques physiques du neurone. Le modèle de Hodgkin-Huxley permet de retrouver cette vitesse de propagation avec une étonnante précision.
Et ce n’est pas tout. Outre l’émission simple d’un potentiel d’action, un grand nombre de comportements observés dans les neurones réels sont correctement décrits par le modèle de Hodgkin-Huxley, comme les modes de décharge par bouffées intermittentes ou à des fréquences variables… Un chercheur, Eugene Izhikevich, s’est amusé à faire une liste des comportements observés dans la réalité qu’un « bon » modèle de neurone doit être capable de reproduire, par exemple, la réponse à un stimulus. Eh bien, le modèle de Hodgkin-Huxley est celui qui en reproduit le plus grand nombre. C’est peut-être même un des cas, rares, où la théorie serait en avance sur l’expérimentation biologique, car certains des comportements chaotiques prédits par ce modèle n’ont pas (pas encore ?) pu être observés.
Alors, est-ce un modèle parfait ?
Malheureusement non, car ce qui fait sa qualité est aussi son principal défaut. Sa complexité est telle que son analyse mathématique n’est pas finie, elle résiste encore aux chercheurs, depuis plus de cinquante ans. Sa mise en œuvre sur ordinateur est coûteuse en termes de temps de calcul et nécessite des schémas d’intégration élaborés.
De fait, de nombreux modèles produits depuis cette époque ne cherchent pas à compléter le modèle de Hodgkin-Huxley, mais au contraire à le simplifier, tout en conservant le maximum de pertinence biologique.
Que retenir d’essentiel ?
Le modèle de Hodgkin-Huxley met en évidence une propriété fondamentale des neurones : ce que les neurones échangent entre eux, ce sont des impulsions. En effet, l’observation biologique et l’étude du modèle montrent que la forme des potentiels d’action importe peu, que leur amplitude étant toujours la même n’a pas d’influence variable. Que reste-t-il alors ? Un neurone qui à un moment précis tire une impulsion. C’est donc le temps qui est déterminant pour décrire le mode de décharge des neurones.
Certains neurones peuvent décharger bien au-delà de cent fois par seconde, ainsi que par bouffées. La fréquence de décharge des impulsions sert parfois à coder une quantité. Par exemple, dans la rétine, une image avec un fort contraste conduira les neurones à décharger à un rythme rapide. Mais la fréquence de décharge ne donne pas tout ! Nous ne sommes qu’au début de l’exploration des codes neuronaux basés sur les impulsions.
Voici un modèle de neurone. Cette applet calcule les valeurs du potentiel de membrane pour la plupart des modes de décharge des neurones.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si l’applet ne s’affiche pas correctement, ou si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
Choisissez un mode et regardez comment le neurone se comporte.
Vous pouvez aussi ajuster vous-même l’intensité du courant de 0 à 100 : vous obtiendrez soit des comportements plausibles, soit des régimes imaginaires inexistants dans la nature.
3. Question de connexion
Un neurone isolé, c’est bien joli, mais ça n’existe pas !
Les modèles de neurones isolés, issus du modèle de Hodgkin-Huxley, nous ont conduits à souligner que les neurones échangent des impulsions entre eux. C’est donc leur fonctionnement en réseau qu’il convient d’étudier maintenant. Pour appréhender comment ils transforment des stimuli en trains d’impulsions, puis ces trains d’impulsions en d’autres trains d’impulsions, et enfin ces trains d’impulsions en commandes musculaires.
L’approche réductionniste montre ici ses limites. Si le modèle de Hodgkin-Huxley est trop complexe pour un neurone, quel espoir avons-nous d’analyser le comportement des milliers de neurones qui composent une colonne corticale, sans parler des 100 milliards de neurones qu’on estime être le nombre moyen de neurones du cerveau humain ?
À ce stade-là, une démarche simplificatrice s’impose. Cette démarche est à la fois pragmatique et extraordinairement féconde si les simplifications sont bien faites. On peut constituer un réseau de neurones formels au comportement individuel rudimentaire et obtenir un comportement collectif étonnamment complexe et riche. Le système acquiert de ce comportement collectif des caractéristiques nouvelles qui ne se réduisent pas à la superposition du comportement des unités le constituant. A contrario, il n’hérite pas forcément de toutes les propriétés de ces éléments. Le phénomène ainsi mis en évidence, qui s’oppose d’une certaine façon au principe réductionniste, s’appelle l’émergence.
Regardons de plus près un réseau de neurones simplifiés, au comportement individuel le plus simple possible, et observons comment la transcription d’observations biologiques élémentaires dans un modèle dont presque toute la complexité biologique a été éliminée fait apparaître un comportement émergent.
Une caricature de neurone… qui sera bien utile !
Pour chaque neurone, on considère son potentiel de membrane. Celui-ci vaut zéro lorsque le neurone est au repos. S’il passe un seuil d’excitabilité S, de valeur fixe, il tire une impulsion, puis revient à zéro. On définit également une variable binaire qui vaut 1 lorsqu’un potentiel d’action est émis, et 0 dans le cas contraire, c’est la loi du « tout ou rien ».
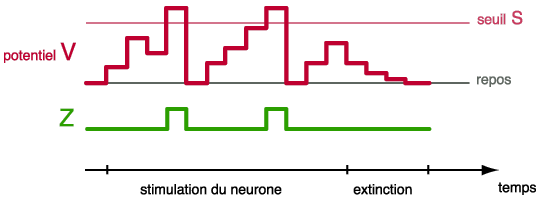
Lorsqu’on applique un courant au neurone, soit le potentiel dépasse le seuil, le neurone tire une impulsion, et le potentiel revient à zéro, soit le potentiel ne dépasse pas le seuil, il se met alors à décroître lentement, par un phénomène de fuite. On modélise ce phénomène par un coefficient k compris entre 0 et 1.
Pour étudier numériquement la dynamique du neurone, on considère le temps comme discret, avec un pas de temps de l’ordre de la période réfractaire, c’est à dire l’intervalle de temps pendant lequel le neurone ne peut pas décharger plus d’une fois. La justification du choix de ce pas de temps nécessiterait des explications qui dépassent le cadre de ce document.
En l’absence de courant, la dynamique d’un tel neurone est triviale. Elle l’est aussi si le courant appliqué est constant. Dans ce cas, si le courant appliqué est suffisant, le neurone va décharger périodiquement. On montre facilement que le courant doit être supérieur à (1-k) S pour que le neurone décharge, et que la période de décharge dépend du paramètre k, du seuil S ainsi que de l’intensité du courant appliqué. Mais si le potentiel est nul au départ et que le courant appliqué est égal à (1-k) S, alors le temps qui s’écoule avant la première décharge est infini ! Un tel système est donc impossible à observer.
Il est utile de préciser l’influence du coefficient k. En effet, ce terme permet de contrôler combien de temps un neurone va garder la mémoire de ses états précédents. Si k=0, alors le potentiel à l’instant t+1 ne dépend pas du tout du potentiel à l’instant t. A contrario, si k=1, alors l’état du neurone dépend de tout le passé. En pratique, la valeur de k qui correspond aux valeurs biologiques est de l’ordre de 0,9 à 0,95.
Ce qui rend la dynamique de chaque neurone intéressante à étudier, et engendre la dynamique du réseau, c’est qu’en pratique le courant appliqué n’est pas constant. En effet, l’évolution du potentiel de chaque neurone dépend de l’influence des neurones qui lui sont connectés. Chaque neurone qui tire connecté au neurone que nous étudions lui ajoute une petite portion de potentiel, dont la valeur est positive si son influence est excitatrice, ou négative si elle est inhibitrice. Chaque neurone peut également en déchargeant provoquer son auto-excitation.
Le potentiel du neurone i à l’instant t+1, noté Vi(t+1), est donc la somme de plusieurs termes :
- le potentiel de i à l’instant t, noté Vi(t), multiplié par k et (1-Zi(t)),
la variable binaire Zi(t) étant égale à 1 si le neurone a déchargé, ramenant donc le potentiel à 0, et égale à 0 dans le cas contraire, le potentiel étant alors réduit en fonction du coefficient k compris entre 0 et 1 qui exprime le phénomène de fuite ; - un courant extérieur, noté Ii(t), qui correspond à une excitation électrique du neurone i à l’instant t due par exemple à un stimulus ;
- et enfin, des coefficients notés Wij, qui modélisent les liens synaptiques, les potentiels d’action provenant des neurones j connectés à i qui ont déchargé à l’instant t.
On l’exprime par l’équation suivante :
Vi(t+1)= k (1-Zi(t)) Vi(t) + Ii(t) + Wi1Z1(t) Wi2Z2(t)… + WinZn(t)
Quelles variables faut-il étudier ?
Les informations échangées par les neurones, sous forme de trains d’impulsions, sont représentées par la variable binaire Z. Son tracé successif représente ce qu’on appelle le codage neuronal. Mais comprendre ce codage est loin d’être trivial. Par exemple, il est complexe d’identifier un stimulus à partir de l’observation des impulsions. Décrypter le codage neuronal dans les neurones réels est sans doute un des défis les plus importants du 21e siècle.
Et qu’en est-il du potentiel V ? Certes, la variable Z se déduit immédiatement de V, mais l’inverse n’est pas vrai. Ne faut-il pas alors également observer ce potentiel ? Heureusement, l’étude théorique de ce modèle donne une réponse qui simplifie le problème. En effet, elle montre qu’au niveau du réseau dans son ensemble, au bout d’un temps suffisamment long, il est inutile de s’intéresser au potentiel V de chaque neurone, car il devient entièrement dépendant des variables Z des autres neurones. La dynamique du réseau est alors entièrement caractérisée par les événements binaires qui se produisent.
Ce résultat peut être démontré rigoureusement dans le cas de notre petit modèle. Cependant, il n’y a pas de résultat analogue pour des réseaux de neurones où la modélisation des neurones est plus élaborée. Il se peut donc qu’une telle propriété n’existe pas. Cette remarque nous amène simplement à nous demander quelle est la « bonne façon » de modéliser un neurone : par son potentiel de membrane ou par l’émission d’événements binaires (les impulsions) ? Là encore, cela dépend des questions que l’on se pose.
Quelle est la dynamique de ce réseau ?
La réponse n’est pas immédiate, même avec deux neurones.
Considérons deux neurones, notés 1 et 2. L’évolution de ces deux neurones est donnée par un système de deux équations :
V1(t+1) = k V1(t) (1-Z1(t)) + W11 Z1(t) + W12 Z2(t)
V2(t+1) = k V2(t) (1-Z2(t)) + W21 Z1 + W22 Z2(t)
On suppose que W22 est supérieur au seuil d’excitation S ; que W12 est positif et supérieur ou égal à (1 – k) S ; que W21 est négatif.
Avec ces hypothèses, si le neurone 2 décharge une fois, alors il décharge la fois suivante par le seul effet de son auto-excitation. Mais si le neurone 1 décharge en même temps, il peut inhiber la décharge du neurone 2. Supposons donc qu’à l’instant t, le neurone 2 décharge, mais pas le neurone 1. Alors l’équation qui donne le potentiel du neurone 1 à l’instant suivant t+1 devient
V1(t+1) = k V1(t) + W12
et cela reste vrai tant que V1(t) reste inférieur au seuil S.
Si le potentiel de départ, V1(0) est inférieur au seuil S, alors tant que le potentiel à l’instant t, V1(t), reste inférieur au seuil S, le potentiel à l’instant t+1 s’écrit :
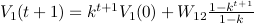
La condition V1(t) < S est équivalente à
V1(0) < f(t),
la fonction f étant définie par :
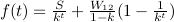
Cette fonction est strictement décroissante si W12 > (1-k) S et f(t) tend vers – ∞ quand t tend vers l’infini. Ainsi, pour W12 > (1-k) S, on calcule un temps τ (les crochets signifiant qu’on considère la partie entière) :
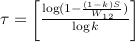
Ce temps τ est tel que quel que soit l’instant t compris entre 0 inclus et τ exclus, il existe un intervalle 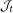 = [f(t), f(t-1)[ ∈ [0, S] tel que quel que soit V1(0) appartenant à cet intervalle
= [f(t), f(t-1)[ ∈ [0, S] tel que quel que soit V1(0) appartenant à cet intervalle 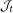 , le neurone 1 déchargera pour la première fois à l’instant t. À partir de cet instant, le neurone 1 déchargeant peut inhiber le neurone 2, qui alors ne décharge plus.
, le neurone 1 déchargera pour la première fois à l’instant t. À partir de cet instant, le neurone 1 déchargeant peut inhiber le neurone 2, qui alors ne décharge plus.
Mais par ailleurs, si W12 tend vers (1-k) S par valeur supérieure, alors τ diverge, et on peut donc retarder à volonté le premier instant de décharge. Cela génère une dynamique qui nécessite un temps d’observation arbitrairement long pour que l’on puisse prédire le futur de l’observation du passé.
Cependant, à ce stade-là, les mathématiques et en particulier la théorie des systèmes dynamiques permettent de décrire cette dynamique pour un nombre de neurones arbitrairement grand, lorsqu’un temps suffisamment long s’est écoulé. On peut ainsi montrer un certain nombre de résultats remarquables.
 |
 |
 |
|
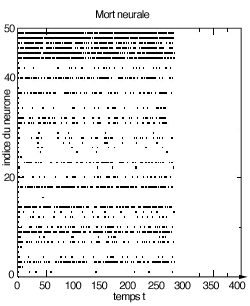
Trois types de régimes. |
||
Si le courant reçu par les neurones est insuffisant, alors les neurones cessent de décharger au bout d’un certain temps, et il ne se passe plus rien. Si au contraire le courant reçu est trop fort, les neurones déchargent de façon périodique, ils ont une activité synchronisée qui se répète sur une période de temps suffisamment longue. Entre ces deux régimes, on constate un cas intermédiaire, où l’évolution des neurones apparaît « chaotique », et pour nous imprédictible. Cela se passe lorsque le courant reçu par certains neurones est proche du seuil de déclenchement. Dans ce cas-là, une toute petite variation du potentiel de membrane peut induire de grands bouleversements. Un neurone décharge, en entraînant d’autres à sa suite…
En changeant un paramètre, par exemple l’intensité du courant extérieur appliqué à un neurone, on peut faire apparaître un comportement collectif complexe. On observe ainsi la réponse dynamique du réseau de neurones à un stimulus. Cette réponse peut correspondre à un changement drastique de comportement.
Précisons bien que ce comportement émergent n’est pas miraculeux, il ne s’agit pas de génération spontanée. Il résulte en fait du couplage d’un grand nombre de neurones et de la dynamique non-linéaire de chacun d’entre eux. Et la théorie nous apprend que ce type de régime n’est probablement pas aussi chaotique qu’il n’y paraît, il s’agirait plutôt d’un régime périodique dont la période serait trop longue pour que nous soyons capables de l’observer.
Ce type de modèle très simplifié de réseau de neurones, où les modèles de neurones sont réduits à un comportement de type tout ou rien, et où les synapses ont une structure déterminée n’évoluant pas dans le temps, permet cependant d’obtenir des résultats mathématiques importants, en combinant des méthodes de mathématiques appliquées, de physique théorique et de simulation numérique.
Et le poids du passé ?
Jusqu’à présent, nous avons négligé un facteur essentiel : le fait que la force des connexions entre les neurones évolue dans le temps. Nous avons supposé que les liens synaptiques étaient des variables indépendantes, sans corrélation entre elles. Cela revient à partir d’une situation dans laquelle on ne dispose d’aucune information préalable sur la structure du réseau et sur son passé. Or c’est en grande partie à cause de ce choix que la dynamique observée semble chaotique.
En réalité, les synapses ne sont pas figées dans le temps, elles changent d’intensité en fonction de l’activité neuronale. On appelle ce phénomène la plasticité synaptique. En raison de cette plasticité, les réseaux de neurones ont la capacité d’apprendre, ils adaptent leur structure à certains stimuli de manière à produire une réaction rapide, viable et reproductible. Dans le cerveau, cette plasticité est ainsi impliquée dans tous les changements d’état, par exemple du sommeil à l’éveil, dans l’apprentissage, dans la mémoire, etc. Sans entrer dans le détail de sa mise en œuvre biologique, le rôle principal de la plasticité synaptique est de créer des corrélations entre les activités neuronales qui dépendent à la fois de l’histoire du réseau et des stimuli auxquels il a été soumis.
Différents types de mécanismes entrent en jeu, mais ils se résument à quelques principes faciles à énoncer. Une règle, proposée par Donald Hebb en 1949, montre que des neurones qui déchargent ensemble se connectent. Un mécanisme complémentaire ajoute que des neurones qui ne sont pas synchronisés se déconnectent.
Deux neurones sont connectés entre eux par une synapse. Le coefficient de cette connexion peut être plus ou moins grand. Il peut être positif ou négatif, la synapse pouvant soit activer soit inhiber le neurone qui reçoit l’impulsion. Et surtout, les synapses ne sont pas figées dans le temps, le coefficient de connexion évolue selon des mécanismes de dépression qui le font diminuer ou de potentiation qui le font augmenter.
Comment sont régis ces mécanismes ? Deux neurones activés ensemble renforcent leur connexion, de sorte que l’activation en sera plus facile à l’avenir. Cette règle, formulée par Donald Hebb en 1949, suffit à rendre compte de la plupart des phénomènes de plasticité synaptique.
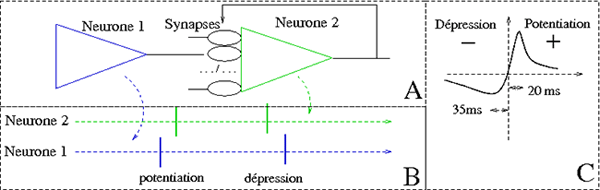
Schéma de deux neurones et de l’évolution de leur connexion.
En A, le neurone 1 (en bleu) envoie des impulsions au neurone 2 (en vert). En B, figurent les impulsions tirées par les deux neurones. Si le neurone 2 tire une impulsion juste après le neurone 1, on suppose que l’impulsion du neurone 1 a pu provoquer celle du neurone 2. Il y a alors potentiation. Mais si le neurone 2 tire longtemps après le neurone 1, il n’y a probablement pas de causalité, la connexion est dépressiée. En C, la courbe montre comment le degré de potentiation ou de dépression dépend du temps relatif entre les impulsions.
En conséquence, modifions les coefficients Wij de notre modèle. À chaque instant, on augmente un peu le coefficient Wij si j a tiré avant i, sinon on le diminue. La dynamique d’évolution de ces coefficients entraîne des corrélations entre eux, ainsi qu’une mémoire de l’activité passée puisque la modification de ces coefficients fait intervenir les instants de décharge des neurones connectés par des synapses. L’imposition d’un stimulus modifie l’activité du réseau, et la plasticité va imprimer cette modification dans la structure même du réseau synaptique.
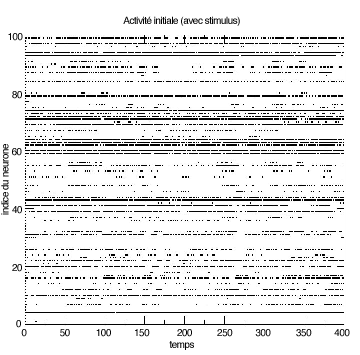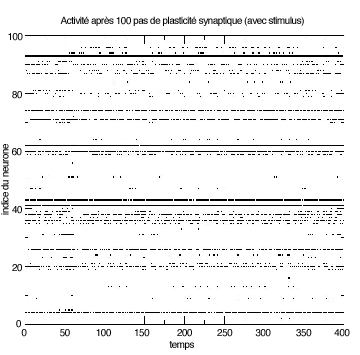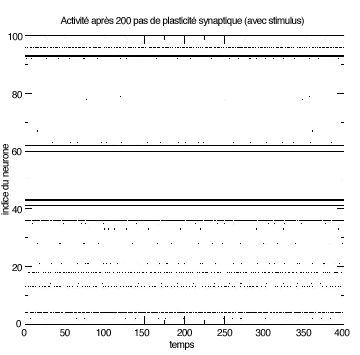
Il en découle qu’après une phase d’adaptation, le tracé des événements est beaucoup moins complexe. Le système a besoin de beaucoup moins d’information pour coder son activité, puisqu’il l’a contrainte à être adaptée au stimulus. En quelque sorte, tout se passe comme s’il connaissait déjà en partie le stimulus qui va l’activer.
 |
 |
|
Effet de la plasticité synaptique. |
|
Pour expérimenter ces mécanismes, nous vous proposons une applet qui simule l’activité d’un tel réseau, comprenant 600 neurones. La dynamique complexe représentée ici varie en fonction de différents paramètres :
- la variabilité de l’entrée, c’est-à-dire l’amplitude du stimulus qui active de l’extérieur le réseau de neurones
- la variabilité des connexions, c’est-à-dire l’amplitude des interactions internes au réseau de neurones
- la plasticité synaptique, c’est-à-dire le fait que ce réseau s’adapte aux stimulus externes et tient compte de son activité passée, ou non.
Si vous jouez sur la variabilité des connexions ou de l’entrée, vous observerez plusieurs formes d’activités : plus ou moins régulières, plus ou moins périodiques. Par exemple, une forte variabilité de l’entrée introduit une dynamique bien irrégulière, mais si la variabilité des connexions est augmentée aussi, alors cette irrégularité a tendance à se stabiliser. Si, ensuite, la plasticité synaptique est introduite, tout change, l’activité du réseau va se stabiliser dans un mode périodique qui sera peu sensible aux variations des paramètres.
Pour accéder à l’applet Java, autorisez les applets du domaine https://interstices.info. Si l’applet ne s’affiche pas correctement, ou si votre navigateur n’accepte plus le plug-in Java, mais que Java est installé sur votre ordinateur, vous pouvez télécharger le fichier JNLP, enregistrez-le avant de l’ouvrir avec Java Web Start.
L’étude des effets de la plasticité synaptique sur la dynamique neuronale reste un problème difficile, qui nécessite de prendre en compte une interaction complexe entre la dynamique des neurones, qui agit sur la structure du réseau synaptique, et la dynamique des synapses, qui modifie le comportement des neurones. Cet aspect, trop peu étudié, semble pourtant le plus important, que l’on cherche à comprendre les capacités d’adaptation, la mémoire, la généralisation des réseaux de neurones biologiques ou que l’on cherche à créer des systèmes inspirés de la biologie, en robotique, en vision artificielle, ou pour de nouvelles architectures d’ordinateurs. À partir des méthodes de la théorie des systèmes dynamiques et de la physique statistique, il est nécessaire d’inventer de nouveaux outils d’analyse.
Pour conclure… et esquisser une réponse
Du point de vue de l’analyse mathématique, le cerveau humain, abordé selon l’optique des réseaux de neurones, n’est pas un « bon modèle », car il est beaucoup trop complexe. Néanmoins, l’analyse mathématique, en développant sans cesse de nouvelles méthodes, est utile pour intégrer dans des systèmes artificiels les nouvelles connaissances acquises sur le cerveau et sa structure. Elle sert aussi à étudier le système nerveux, moins élaboré, d’organismes aussi simples que des vers de terre. On connaît par exemple entièrement le réseau neuronal d’un ver comme Caenorhabditis elegans. L’analyse mathématique d’un tel réseau, afin d’associer des comportements du ver, comme la reptation ou la recherche de nourriture, à des comportements dynamiques de son réseau de neurones, est peut-être une tâche accessible avec les méthodes mathématiques et numériques actuelles. En ce sens, le système nerveux de C. elegans est un « bon modèle » de réseau de neurones !
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Bruno Cessac

Christine Leininger
Cheffe de projet médiation scientifique à la direction de la culture et de l'information scientifiques d'Inria.
