
Le chaos linéaire : un paradoxe ?
L’effet papillon
Depuis la fin du 19e siècle, les mathématiciens se sont efforcés de comprendre la nature du chaos. Un phénomène souvent rattaché à cette notion porte le nom d’effet papillon : le simple battement d’ailes d’un papillon au Brésil pourrait causer une tornade au Texas. Autrement dit, une perturbation minime pourrait avoir à long terme des conséquences réellement significatives. En mathématique, on parle de la sensibilité aux conditions initiales.
Une autre caractéristique du chaos réside en l’existence de conditions initiales conduisant à n’importe quelle configuration du système : une navette spatiale partant d’un endroit privilégié finirait par visiter chaque recoin de l’espace. Dans le jargon mathématique, sa trajectoire porterait le nom d’orbite dense.
Le chaos en mathématique
En 1986, le mathématicien américain R. Devaney a proposé une définition du chaos qui, à première vue, impose des conditions très fortes. Selon lui, un système dynamique est chaotique s’il vérifie, à la fois, les trois propriétés suivantes :
- la sensibilité aux conditions initiales,
- l’existence d’une orbite dense,
- le passage, près de chaque point, d’une orbite périodique.
Les deux dernières conditions entraînent qu’on retrouve une orbite dense et une orbite périodique près de chaque point.

La sensibilité aux conditions initiales : une table de billard avec un obstacle. La boule, lancée au départ avec une différence d’angle très faible, suit une trajectoire très différente.
 Une orbite périodique : celle de la comète de Halley. Cette comète gravite autour du Soleil selon une orbite elliptique, sa période est d’environ 75 ans. |
 Une orbite dense dans un anneau. |
Un exemple simple
Les conditions de Devaney sont-elles trop fortes ? Au contraire, elles sont vérifiées par un système dynamique aussi simple que celui décrit par la fonction φ(x) = 1 -|2x-1| avec 0 ≤ x ≤ 1.
Un système dynamique discret est donné par une fonction φ d’un ensemble d’objets, noté X, vers lui-même. Cette fonction se note φ : X → X.
Si on appelle x0 l’état initial, les états suivants se calculent grâce à la formule xn+1 = φ(xn), avec n = 0, 1, 2… On interprète n comme le temps écoulé. L’orbite d’un point x0 est alors donnée par la suite (x0, x1, x2, x3…).
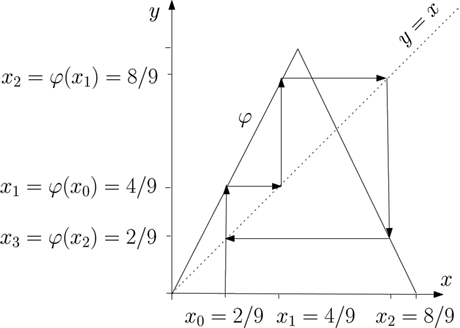
Par exemple, si nous choisissons x0 = 2/9 comme état initial, nous trouvons que x1 = φ(2/9)=4/9, puis x2=φ(4/9)=8/9 et x3 = φ(8/9) = 2/9. Comme x3 coïncide avec x0, on en déduit que l’orbite de x0 est donnée par (2/9, 4/9, 8/9, 2/9, 4/9, 8/9, 2/9…). Le point x0 a donc une orbite périodique de période 3.
Il est facile de trouver d’autres orbites périodiques. En fait, près de chaque point, on peut trouver un point avec une orbite périodique. La troisième condition du chaos selon Devaney est donc vérifiée par ce système.
Concernant la sensibilité aux conditions initiales, contentons-nous de l’illustrer par un exemple, montré dans le tableau ci-dessous. Pour l’état initial x0 = 0.16, on obtient x6 = 0.24, tandis que pour l’état x0 = 0.17 légèrement différent, on obtient x6 = 0.88, très éloigné de 0.24.
| Orbite originale | Orbite perturbée | |
|---|---|---|
| x0 | 0.16 | 0.17 |
| x1 | 0.32 | 0.34 |
| x2 | 0.64 | 0.68 |
| x3 | 0.72 | 0.64 |
| x4 | 0.56 | 0.72 |
| x5 | 0.88 | 0.56 |
| x6 | 0.24 | 0.88 |
Bien que cela soit plus difficile à voir, on peut également montrer que ce système possède des orbites denses. Le système dynamique donné par la fonction φ est donc chaotique dans le sens de Devaney. Il s’agit là d’un exemple très simple de système non-linéaire de dimension finie, mais qu’en est-il des systèmes linéaires ?
Le système défini par la fonction φ n’est pas linéaire. En effet, pour qu’il soit linéaire, il faudrait notamment que pour tous les points x et y, on vérifie φ(x+y) = φ(x) + φ(y).
Or par exemple, si x = 0.3 et y = 0.4
alors φ(x+y) = φ(0.7) = 0.6,
tandis que φ(x) + φ(y) = 0.6 + 0.8 = 1.4,
et donc φ(x+y) ≠ φ(x) + φ(y).
L’espace des nombres réels est de dimension finie, égale à 1. Il suffit de multiplier un nombre non nul, par exemple 1, pour obtenir tous les nombres. Comme la fonction φ est définie sur un sous-ensemble des réels, on parle d’un système de dimension finie.
L’existence du chaos linéaire
En 1991, G. Godefroy et J. H. Shapiro ont proposé d’accepter la définition du chaos au sens de Devaney même pour les systèmes linéaires. Ils avaient alors à l’esprit un vieux résultat de G. R. MacLane datant de 1952.
Celui-ci affirmait que l’opérateur de dérivation φ(f)=f′ qui associe à chaque fonction dérivable f sa dérivée f′ possède une orbite dense.
Le système défini par l’opérateur de dérivation est bien linéaire.
Si f et g sont deux fonctions dérivables et a est un nombre réel quelconque, alors
(f+g)′ = f′ + g′ et (af)′= af′.
L’orbite d’une fonction indéfiniment dérivable pour cet opérateur est donnée par ses dérivées successives ( f, f′, f′′, f′′′, f(4), f(5)…). Il existe donc, selon MacLane, une fonction indéfiniment dérivable f telle que pour n’importe quelle autre fonction g, il y a une dérivée n-ème de f qui approche g : f(n) ≈ g. D’autre part, il est facile de trouver des points périodiques de ce système. Par exemple, étant donné que (ex)′ = ex, la fonction exponentielle est un point de période 1. La fonction sinus, quant à elle, est un point de période 4. En étudiant plus en profondeur l’opérateur de dérivation, Godefroy et Shapiro sont alors parvenus à montrer que celui-ci possède un ensemble dense de points périodiques et qu’il est même chaotique au sens de Devaney.
Le chaos linéaire existe donc bel et bien.
Étonnamment, comme l’opérateur de dérivation le montre, il n’est même pas nécessaire de construire des opérateurs d’une grande complexité pour observer ce phénomène.
D’où provient l’ignorance du chaos linéaire ?
Imposer la linéarité à un système constitue malgré tout une restriction importante : le chaos linéaire ne peut être observé que pour des systèmes portant sur des espaces de dimension infinie comme, par exemple, l’espace de toutes les fonctions indéfiniment dérivables. C’est sans doute cette absence du chaos linéaire en dimension finie qui est à la base de sa méconnaissance. Néanmoins, dès que cette barrière est franchie, tout est possible. Un résultat de N. Feldman datant de 2001 montre qu’un système linéaire de dimension infinie peut adopter n’importe quel comportement irrégulier observé pour un système non-linéaire.
L’espace des fonctions indéfiniment dérivables est de dimension infinie, car il faut un nombre infini de fonctions de base pour représenter toutes les fonctions de cet espace.
Par exemple, les monômes f(x) = xk, avec k = 0, 1, 2… forment un ensemble indépendant infini : aucun monôme ne peut être exprimé comme une combinaison linéaire des autres monômes. Cependant, pour arriver à une base, il faut encore y ajouter d’autres fonctions !
Une théorie en pleine expansion…
Le travail de Godefroy et Shapiro a été un véritable déclencheur pour la recherche sur le chaos linéaire. De nos jours, de nombreuses équipes un peu partout dans le monde étudient ce phénomène. En 2004, deux jeunes mathématiciens français, S. Grivaux et F. Bayart, ont observé un comportement inouï : il existe des orbites, appelées fréquemment récurrentes, qui sont denses et montrent pourtant un fort aspect de périodicité. Plus précisément, si on regarde n’importe quel point de l’espace, il existe un temps n tel que l’orbite passe près de ce point au moins une fois avant l’instant n, au moins deux fois avant l’instant 2n et ainsi de suite.
Essayez un peu d’imaginer le comportement d’une navette dans notre univers si sa trajectoire vérifiait une telle propriété. Si par exemple, pour le Soleil, on avait n = 10 ans, la navette passerait près du Soleil au moins une fois en 10 ans, au moins deux fois en 20 ans, au moins trois fois en 30 ans, et ainsi de suite. De plus, la navette visiterait de la même façon chaque étoile de l’univers – avec une « période » n différente, bien sûr. Même si c’est difficilement concevable, de telles orbites existent.
… et des questions toujours ouvertes
Alors qu’un tel comportement n’avait même pas été observé auparavant pour un système non-linéaire, Grivaux et Bayart ont montré que l’opérateur de dérivation possède une orbite fréquemment récurrente. Il semble dès lors naturel de se demander si chaque système chaotique possède une telle orbite. Cependant, à l’heure actuelle, personne ne connaît la réponse à cette question.
Le chaos linéaire est loin de nous avoir livré tous ses secrets.
Une première version de ce document est parue dans le magazine « élément » de l’Université de Mons, n°05, en mars 2011.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Karl Grosse-Erdmann

Quentin Menet