Le morpion, simple comme un jeu d’enfant ?

Le morpion fait partie des premiers jeux abstraits, sans hasard ni information cachée, qui se jouent à deux et que l’on découvre dès notre plus jeune âge. À tour de rôle, deux personnes dessinent un rond (Olivia) ou une croix (Xavier) sur une case libre d’une grille \(3×3\). Celui ou celle qui réussit à aligner trois symboles identiques lui appartenant remporte la partie. Dans le cas contraire, la partie est un match nul. Il est facile de se convaincre que lorsque chacun joue optimalement, personne n’est capable d’aligner trois symboles identiques et la partie s’achève sur un nul. Cette propriété, ainsi que le faible nombre de coups possibles au morpion, n’incitent pas vraiment à enchaîner les parties entre amis !

Alors comment généraliser ce jeu afin de le rendre plus attractif dans son analyse sans pour autant dénaturer son aspect ludique ? Il y a naturellement deux paramètres du morpion que l’on peut faire varier :

• la taille \(n\) de la grille
• la longueur \(k\) des alignements qui permettent de gagner

On va noter \(M(n,k)\) le jeu du morpion généralisé défini de la façon suivante : Olivia et Xavier dessinent à tour de rôle un de leurs symboles sur une grille carrée de \(n×n\) cases. Olivia commence à jouer. Le premier joueur qui réussit à aligner \(k\) symboles identiques lui appartenant remporte la partie.

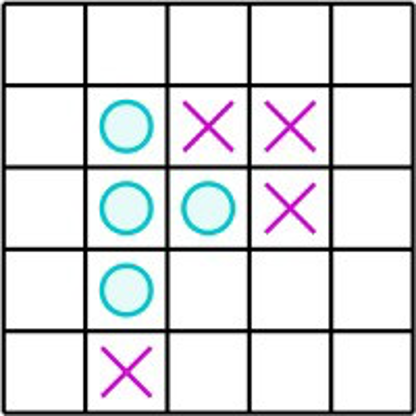
Le morpion généralisé \(M(5,4)\) en cours de jeu. Au prochain tour, Olivia gagne en jouant dans la case \((1,2)\).

Cette définition généralise clairement le morpion habituel qui correspond au jeu \(M(3,3)\). Elle recouvre également un jeu moins bien connu du grand public européen mais très présent en Chine ou au Japon : le Gomoku. Il s’agit d’aligner \(5\) pions de sa couleur sur un plateau de jeu de Go (c’est-à-dire une grille \(19×19)\). Ce jeu correspond donc au morpion généralisé \(M(19,5)\). Dans sa variante sur un plateau \(15×15\) (avec quelques contraintes supplémentaires qui permettent d’équilibrer le jeu), il possède même un championnat du monde officiel !

À l’image du Puissance \(4\), des dames ou encore des échecs, le morpion généralisé fait partie de la famille des jeux à deux, sans hasard et à information parfaite, où l’on joue sans passer son tour. Pour tous ces jeux, il n’est pas très difficile de se convaincre qu’il existe forcément une stratégie gagnante pour l’un des deux participants (quoi que fasse l’autre), ou alors une stratégie qui conduit à un nul pour les deux. Les fidèles d’Interstices l’auront d’ailleurs appris dans cet article de Rémi Coulom : il suffit en effet de construire ce qu’on appelle l’arbre de jeu (la racine est la position de départ, et l’on met un arc entre deux positions s’il existe un coup qui permette de passer de l’une à l’autre).

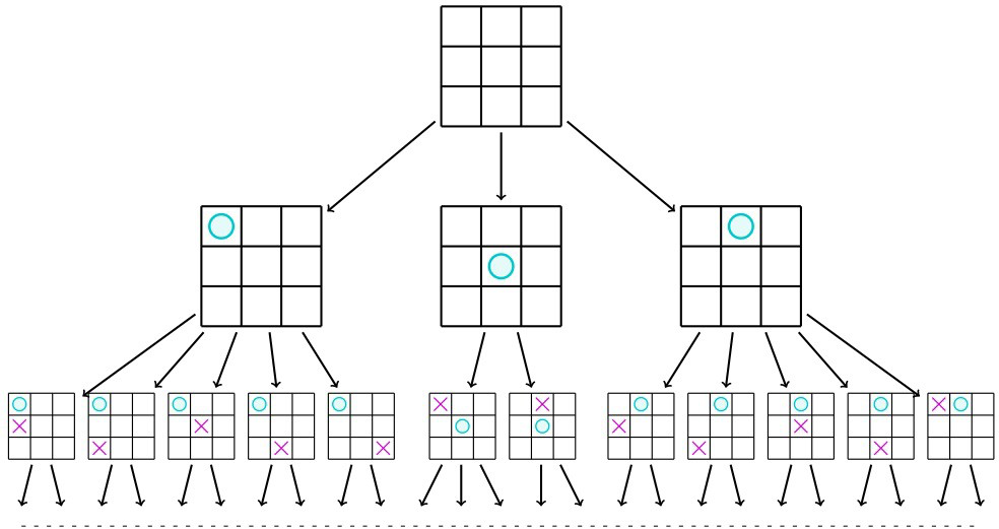
Le début de l’arbre de jeu du morpion.

En parcourant l’arbre de jeu depuis les feuilles (qui correspondent aux fins de parties) jusqu’à la racine, on peut étiqueter chaque position de jeu en fonction de celui ou celle qui gagne. L’étiquette de la racine donne ce qu’on appelle l’issue du jeu, à savoir gagnant pour Olivia, gagnant pour Xavier ou bien nul. Ainsi, un jeu dont l’issue est favorable à Xavier signifie qu’il peut toujours gagner peu importe comment joue Olivia.

La problématique majeure, à la fois en informatique et en mathématiques, devient alors de calculer l’issue d’un jeu donné. Dans des cas simples comme le morpion classique, on peut construire intégralement l’arbre de jeu et appliquer la méthode ci-dessus : comme expliqué dans l’article de Rémi Coulom cité précédemment, c’est de cette façon qu’on démontre que le morpion a pour issue une partie nulle. En revanche, dès que la taille du plateau devient un peu plus grande, l’arbre de jeu devient trop gros et il va falloir trouver d’autres approches pour calculer l’issue. Par exemple, au jeu d’échecs, le nombre de positions de jeu est estimé à \(10^{43}\), et il passe même à environ \(10^{171}\) pour le jeu de Go, ce qui est plus grand que le nombre d’atomes dans l’univers ! Construire l’arbre de jeu dans de telles circonstances n’est même pas une idée envisageable.

Nous allons voir dans la partie suivante ce que nous savons des issues pour le morpion généralisé, sans avoir à calculer l’arbre de jeu.

Ce que l’on sait sur le morpion généralisé

Faire des petits alignements

Si aligner trois symboles sur une grille \(3×3\) est une tâche impossible contre un ou une adversaire aguerri·e, dès que la grille est un peu plus grande, cela devient très facile ! En effet, en jouant sur une des quatre cases centrales sur une grille \(4×4\), Olivia pourra, à son deuxième coup, jouer une autre case centrale et créer deux pièges, ce qui lui assure une victoire à son troisième coup. Il existe donc une stratégie gagnante (triviale) pour Olivia (c’est-à-dire pour la personne jouant en premier) au jeu \(M(4,3)\) et donc à tous les jeux \(M(n,3)\) pour \(n\geq 4\).

Pour aligner quatre symboles, ce n’est pas aussi simple, mais on peut se convaincre assez facilement qu’il est possible d’aligner quatre symboles pour Olivia dès \(n=6\). Par contre, \(M(5,4)\) et donc \(M(4,4)\) ont pour issue une partie nulle.

Pour cinq symboles, la complexité augmente considérablement ! On ne peut plus résoudre ces cas à la main. Des chercheurs taïwanais ont montré en 2019 à l’aide d’un programme ayant tourné trois jours durant que \(M(8,5)\) (et donc les grilles plus petites aussi) ont pour issue une partie nulle.

Pour des grilles plus grandes, Allis, un chercheur hollandais, a utilisé en 1994 des techniques d’intelligence artificielle pour parcourir l’arbre du jeu \(M(15,5)\), et a pu démontrer avec son programme que le premier joueur avait une stratégie gagnante pour ce jeu, et donc pour toutes les grilles plus grandes. Par contre, pour des valeurs de \(n\) comprises entre \(9\) et \(14\), on ne sait pas s’il est possible de gagner à coup sûr au jeu \(M(n,5)\), cela reste une question ouverte.

Empêcher son adversaire d’aligner trop de symboles

Considérons maintenant des valeurs plus élevées de \(k\).

Intuitivement, plus le nombre de symboles à aligner est grand, plus il est facile d’empêcher son adversaire de gagner. Autrement dit, le jeu \(M(n,k)\) pour un \(k\) suffisamment grand a de grandes chances de finir en match nul. À partir de quelle valeur de \(k\) le jeu est-il toujours nul ? On donne ici une stratégie pour Xavier qui empêche Olivia d’aligner neuf ronds. Olivia pourrait faire la même chose pour empêcher Xavier d’aligner neuf croix. Ce qui revient à dire que l’issue du jeu \(M(n,9)\) est une partie nulle, quelle que soit la valeur de \(n\).

La stratégie de Xavier est la suivante. Il va commencer par paver la grille avec un motif en forme de \(H\) de la manière suivante.

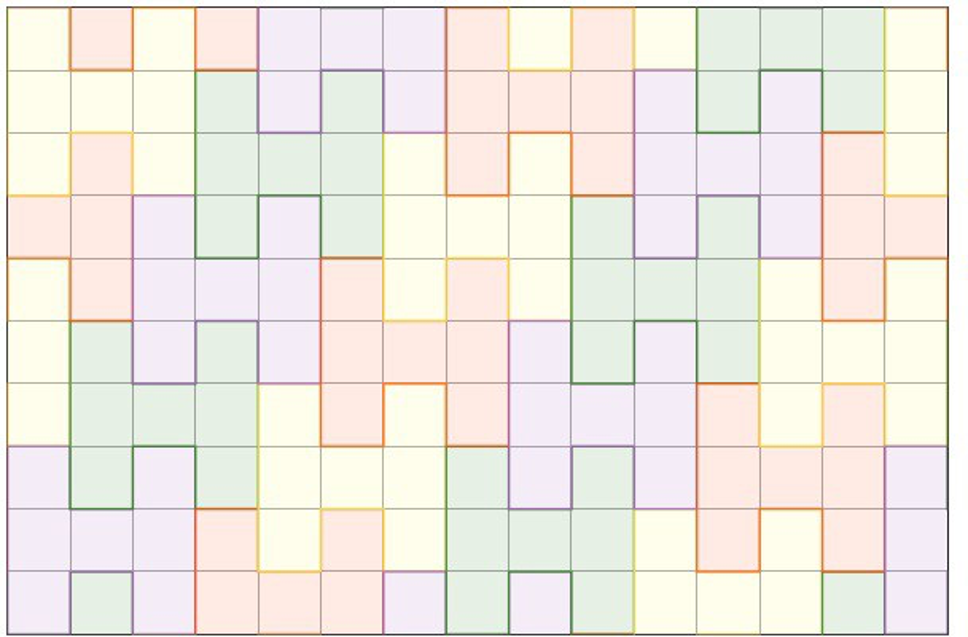
Pavage de la grille \(10×15\) avec des \(H\);

Pourquoi avoir choisi ce pavage ? C’est parce qu’il a la propriété que tout alignement de neuf cases va intersecter un motif \(H\) de l’une des manières suivantes :

• sur trois cases de l’une des diagonales ;
• sur les trois cases de la verticale de droite ;
• sur les trois cases horizontales.

Tout alignement de neuf cases rencontre le motif \(H\) de l’une de ces \(4\) manières ;

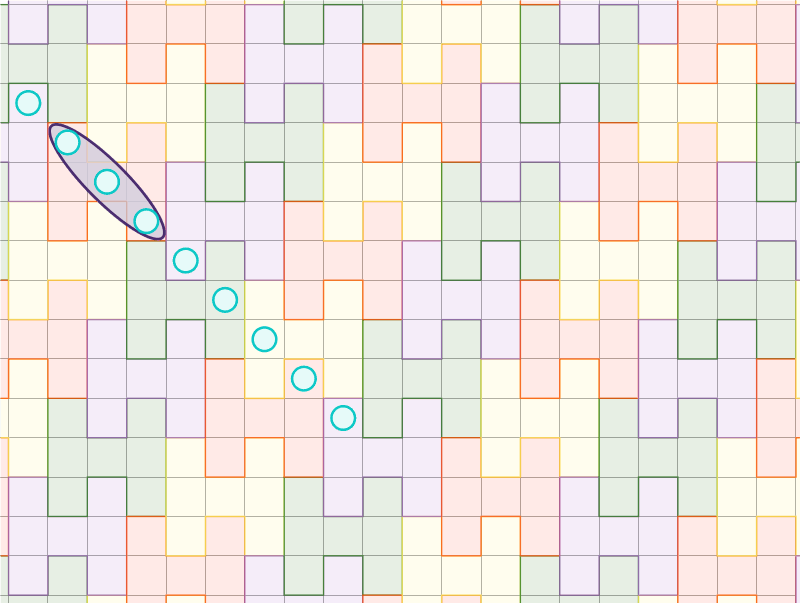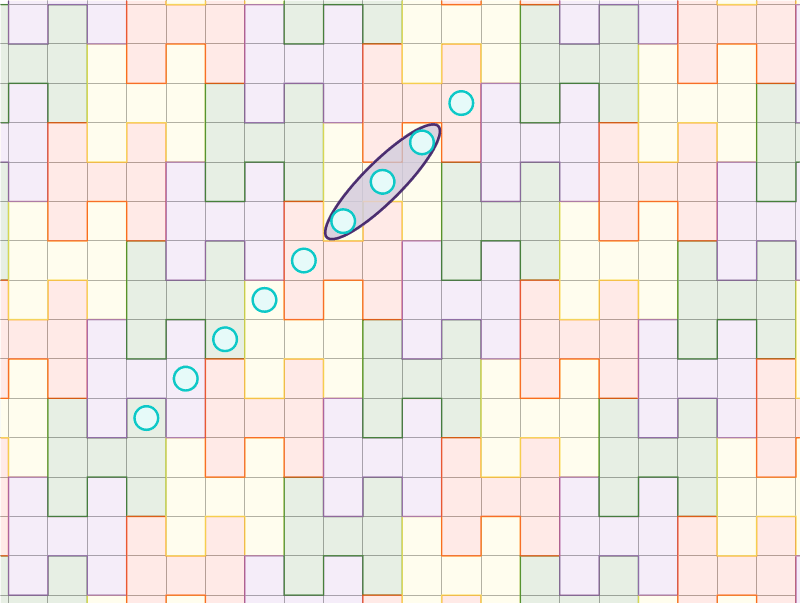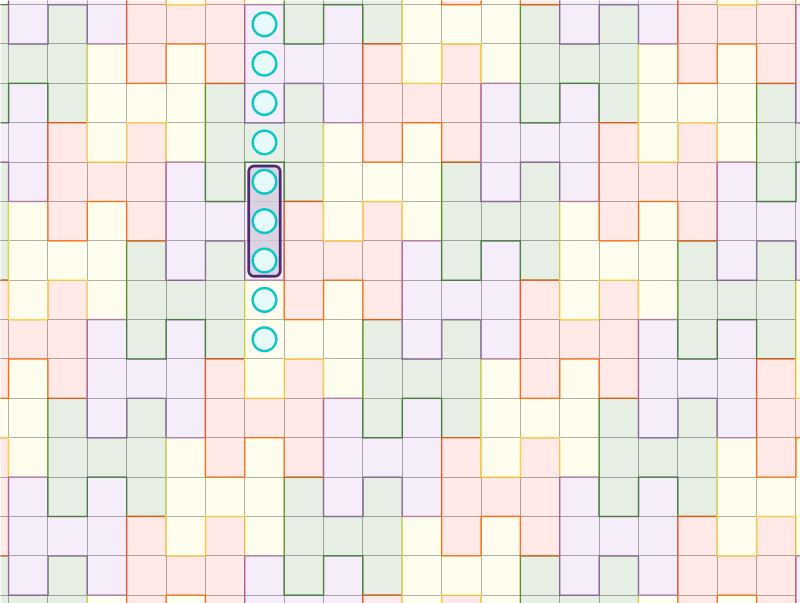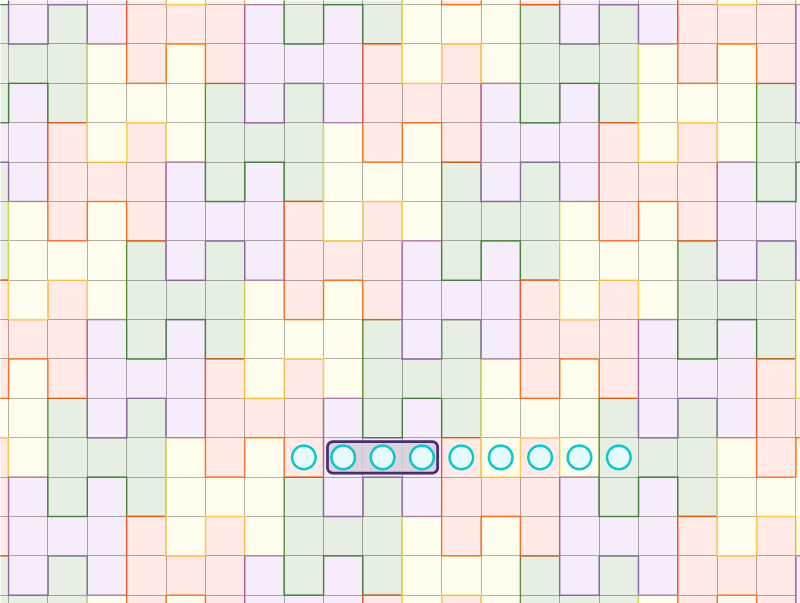
L’animation ci-dessus illustre que pour tout alignement potentiel de \(9\) ronds d’Olivia, un motif \(H\) du pavage est touché de l’une des quatre façons décrites précédemment. Ainsi pour empêcher Olivia d’aligner neuf symboles, Xavier doit juste l’empêcher d’aligner trois symboles sur chaque \(H\) selon l’un des quatre types d’alignements.

Si l’on considère un seul \(H\), ce n’est pas très compliqué de bloquer ces quatre alignements. Voilà une stratégie possible (dite stratégie du \(H\)) :

• Si Olivia ne joue pas au centre, Xavier joue au centre. Il ne reste plus que la verticale de droite à bloquer, et il reste deux coups possibles, il pourra donc bloquer la verticale dès qu’Olivia jouera dedans.
• Si Olivia joue au centre, Xavier joue la case à droite du centre. Il reste alors les deux diagonales. À ce moment-là, Xavier va « coupler » les deux cases restantes de chaque diagonale : dès qu’Olivia jouera une case d’une diagonale, il jouera l’autre.

Si le \(H\) est partiel (car au bord du plateau), Xavier n’a besoin de bloquer que les motifs complets de trois cases.

Sur la grille en entier, Xavier applique la stratégie du \(H\) sur chacun des \(H\) où Olivia joue : quand Olivia joue dans un \(H\), il répond dans le même \(H\) avec la stratégie ci-dessus. De cette manière, Xavier va empêcher les quatre alignements de trois ronds sur chaque \(H\), et donc tout alignement de neuf ronds sur la grande grille. Il assure donc le match nul !

Cela règle le cas du jeu \(M(n,9)\), et de fait de tout jeu \(M(n,k)\) pour \(k>9\) car il faudra déjà aligner \(9\) symboles avant d’en aligner plus.

Et pour des valeurs plus petites de \(k\) ? Pour \(k=8\), une stratégie similaire existe, cette fois-ci avec le pavage suivant :

Le pavage pour huit symboles.

En étudiant un peu ce pavage, on peut s’apercevoir que tout alignement de huit cases rencontre un motif sur un des dix ensembles dessinés ci-dessous. Pour empêcher un joueur d’aligner huit symboles, il suffit donc de trouver une stratégie sur le motif pour le second joueur qui permette de bloquer tous ces ensembles. Nous laissons le lecteur ou la lectrice motivé.e trouver cette stratégie ! Cela règle en tout cas le sort de tous les jeux \(M(n,8)\).

Un alignement de huit symboles croise toujours le motif sur un de ces dix ensembles.

Entre les deux ?

Comme on vient de le voir, si \(n\) est suffisamment grand, le premier joueur gagne au jeu \(M(n,k)\) pour \(k\leq 5\) alors que le jeu a pour issue un match nul pour \(k\geq 8\). Que se passe-t-il pour \(k=6\) et \(k=7\) ?

Ces questions sont actuellement ouvertes ! Existe-t-il une grille suffisamment grande où il sera possible d’aligner \(6\) ou \(7\) symboles ? La communauté de recherche sur le sujet a tendance à penser que la réponse à cette question est négative : on peut toujours empêcher un joueur d’aligner \(6\) (ou \(7\)) symboles. En effet, les stratégies pour les matchs nuls pour \(8\) et \(9\) symboles n’étant pas très compliquées, on a tendance à croire qu’elles pourraient peut-être s’étendre… alors qu’aligner six symboles semble très difficile !

Prenons un peu de hauteur

Les jeux positionnels

Le jeu \(M(n,k)\) fait partie d’une famille de jeux plus généraux : les jeux positionnels.

Les jeux positionnels sont des jeux à deux joueurs, sans hasard et à information complète. Ils se jouent sur un ensemble de points \(S\) appelés sommets. Sur cet ensemble \(S\), on définit des ensembles gagnants qui sont des sous-ensembles de sommets. Graphiquement, on représente souvent ces structures comme des points dans le plan répartis dans des « patates » (qui correspondent aux ensembles gagnants).

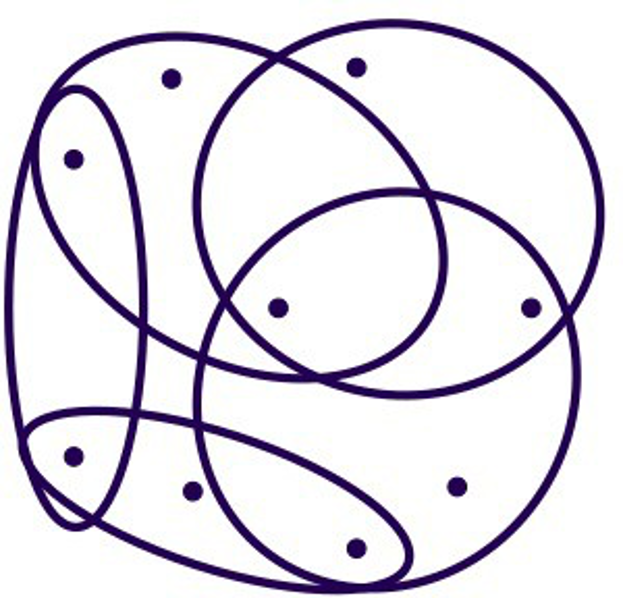
Le plateau d’un jeu positionnel : les points sont les coups à jouer, les « patates » sont les ensembles gagnants.

Les règles du jeu sont les suivantes : alternativement, Olivia (qui commence) et Xavier (second joueur) choisissent un sommet libre et le marquent avec leur symbole (respectivement \(O\) et \(X\)). Le premier joueur qui réussit à remplir un ensemble gagnant avec ses propres symboles gagne la partie. Il peut y avoir match nul si personne n’arrive à remplir un ensemble gagnant.

Comme annoncé précédemment, on constate que le morpion généralisé \(M(n,k)\) fait partie des jeux positionnels. L’ensemble \(S\) de sommets correspond aux \(n^2\) cases du plateau de jeu. Les ensembles gagnants correspondent aux alignements de \(k\) cases dans la grille. La correspondance entre les deux jeux est directe, puisque aligner \(k\) symboles dans la grille de morpion signifie bien marquer tous les sommets de l’ensemble gagnant correspondant.

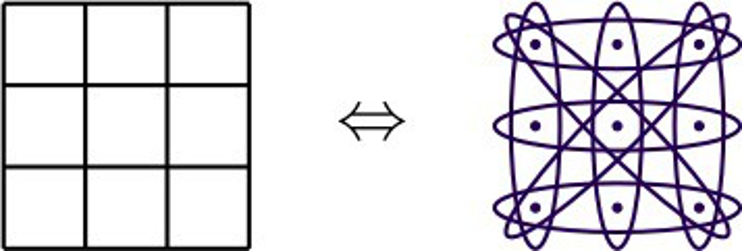
Le morpion standard vu comme un jeu positionnel.

La famille des jeux positionnels a commencé à être considérée par les communautés mathématique et informatique dans les années 1960 et 1970.

Dès lors, ces jeux ont été de plus en plus étudiés par les scientifiques, à la fois de part leur intérêt en terme de résolution, mais aussi parce qu’ils représentent souvent des jeux bien connus des joueurs. Outre le morpion et le GoMoku, on peut citer le jeu de plateau Hex, ou encore le Puissance 4 (avec une petite adaptation de la définition pour prendre en compte la gravité des pièces) qui font partie de cette famille de jeux.

Parmi les résultats bien connus du domaine des jeux positionnels, on peut citer le résultat suivant (en supposant qu’Olivia et Xavier jouent parfaitement, pour rappel) :

Théorème

Dans un jeu positionnel, le second joueur (ici Xavier) ne peut jamais gagner.

Ce résultat très élégant porte une certaine frustration pour Xavier : en tant que second joueur, il ne peut en effet pas faire mieux qu’un match nul. Dès lors, les recherches principales sur les jeux positionnels consistent à décider si l’issue du jeu est favorable à Olivia ou bien un match nul.

Plus précisément, les informaticiens et informaticiennes s’intéressent à la recherche d’un algorithme rapide qui permet de calculer cette issue. Il a été démontré que dans le cas général (c’est-à-dire avec un \(S\) et des ensembles gagnants quelconques), il est impossible de trouver un tel algorithme (on dit en informatique que le problème est PSPACE-complet). Par conséquent, la communauté scientifique va s’intéresser à des jeux positionnels particuliers pour lesquels on peut espérer trouver des méthodes efficaces quant au calcul de l’issue. C’est le cas par exemple lorsque tous les ensembles gagnants sont de taille \(3\) (comme au morpion standard), où un résultat récent de 2023 de Galliot, Gravier et Sivignon vient de prouver qu’on sait construire un algorithme efficace qui calcule l’issue. Il existe aussi d’autres situations où l’on peut construire des stratégies efficaces pour obtenir l’issue du jeu, notamment lorsqu’il s’agit d’un nul. C’est l’objet de la partie suivante.

Des stratégies pour assurer le nul

Nous donnons ici deux stratégies générales pour les jeux positionnels qui permettent d’empêcher le premier joueur (ici Olivia) de remplir un ensemble gagnant suivant certaines conditions. Nous illustrons ces stratégies avec le jeu \(M(n,k)\).

Stratégie utilisant la notion de danger

La première stratégie utilise la notion de danger. Le danger est une valeur donnée à chaque ensemble gagnant pour évaluer à quel point cet ensemble est dangereux pour Xavier. Il est élevé lorsque l’ensemble gagnant est presque rempli par Olivia, alors qu’il doit être très faible lorsqu’il reste beaucoup de sommets libres, voire nul lorsque Xavier a déjà joué dedans.

Le danger d’un ensemble gagnant \(F\) est ainsi défini de manière formelle :

• Si Xavier n’a pas joué dans \(F\), alors le danger de \(F\) est \(\frac{1}{2^{\ell}}\) où \(\ell\) est le nombre de sommets encore libres dans \(F\)
• Si Xavier a déjà joué dans \(F\), alors le danger de \(F\) est \(0\).

Ainsi le danger est situé entre \(0\) et \(1\). La valeur \(1\) correspond à une victoire d’Olivia où tout l’ensemble gagnant est rempli. Plus il y a de sommets libres, plus le danger est petit. Le danger total d’un jeu positionnel est la somme des dangers de chaque ensemble gagnant.

Sur la figure ci-dessous, Olivia a déjà joué une fois. Le danger de chaque ensemble gagnant est indiqué en rouge. Le danger total vaut \(1/2+1/4+2*1/8+1/16=17/16\).

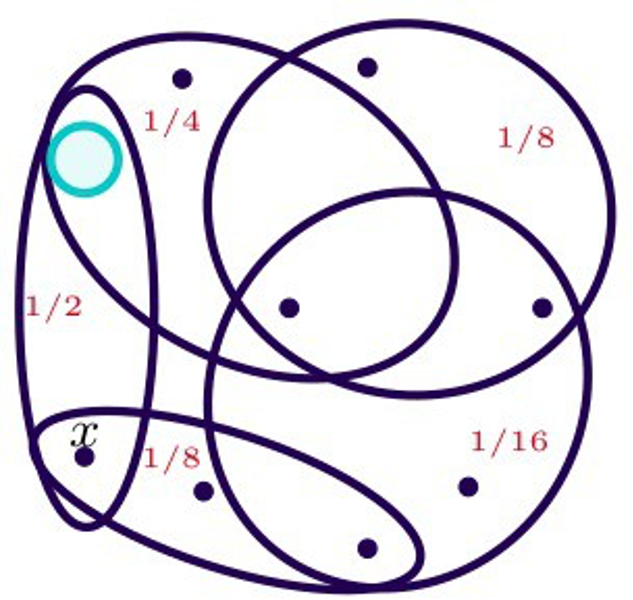
Les valeurs en rouge correspondent aux valeurs du danger de chaque ensemble gagnant.

Intuitivement, Xavier doit contrôler le danger pour empêcher Olivia de gagner. Pour cela, il peut par exemple choisir de jouer le sommet qui diminue le plus le danger total. Dans l’exemple précédent, c’est le sommet \(x\) qui fait le plus descendre le danger : en jouant ce sommet, le danger descend de \(5/8\) et ne vaut plus que \(7/16\).

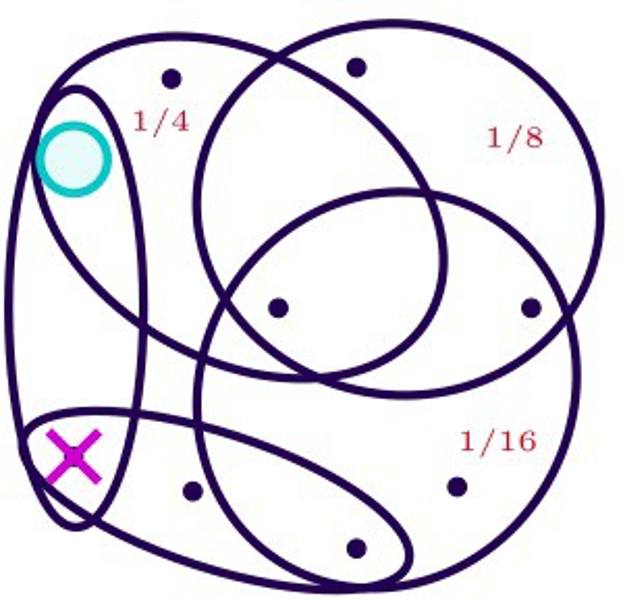
Après le coup de Xavier, il n’y a plus que trois ensembles gagnants qui sont dangereux. Le danger total vaut \(7/16\).

Paul Erdös et John L. Selfridge ont montré qu’avec cette stratégie, si avant le tour de Xavier le danger total est plus petit que \(1\), alors cette stratégie permet de gagner.

Théorème d’Erdös-Selfridge : Si c’est le tour de Xavier et que le danger total est strictement plus petit que \(1\), alors Xavier peut empêcher Olivia de gagner.

Notons que dans le théorème d’Erdös-Selfridge, c’est au tour de Xavier de jouer. Si c’est Olivia qui va jouer, il faut que le danger soit plus que \(1/2\) pour assurer une victoire. En effet, à son premier coup, Olivia peut multiplier le danger total par au plus \(2\) car le danger de chaque ensemble gagnant où elle joue est multiplié par \(2\).

Nous illustrons cette stratégie basée sur le danger avec le jeu \(M(5,5)\). Dans ce jeu, le danger de chaque ensemble gagnant est de \(1/32\). Il y a \(12\) ensembles gagnants donc le danger total vaut \(12/32=0.375<1/2\). À son premier coup, Olivia peut toucher au maximum quatre ensembles gagnants dont le danger passe à \(1/16\). Le danger total vaut alors au maximum \(8/32+4/16=0.5\). Le théorème d’Erdös-Selfridge s’applique et Xavier peut gagner en jouant toujours le sommet diminuant le plus le danger.

Dans l’application ci-dessous, nous avons programmé cette stratégie. Vous pouvez jouer le rôle d’Olivia, le programme joue le rôle de Xavier et répond selon la stratégie du danger. Les cases sont colorées en fonction de leur effet sur le danger : plus une case est rouge, plus elle le fera diminuer (pour Xavier) ou augmenter (pour Olivia). Le graphique à droite indique la valeur du danger. La partie s’arrête lorsque le danger vaut \(0\) : cela signifie qu’Olivia n’a plus aucune chance de gagner !

La condition d’avoir le danger total plus petit que \(1\) est assez rare en pratique. Cependant, jouer un coup qui a une grosse influence sur le danger est souvent un bon coup. Aussi, si à un moment donné le danger descend sous la valeur \(1\), alors on est sûr d’empêcher notre adversaire de gagner.

Par ailleurs, dans cette stratégie, Xavier ne cherche absolument pas à gagner mais seulement à empêcher Olivia de le faire. Il ne fait par exemple aucune menace avec ses coups, il se prive ainsi de certaines possibilités. Le jeu \(M(5,4)\) illustre cela. Sur ce jeu, Xavier a normalement une stratégie pour assurer la partie nulle. Cependant, s’il suit uniquement la stratégie du danger, il est possible pour Olivia de gagner. Y arriverez-vous ?

Stratégie d’appariement

Une seconde stratégie pour que Xavier assure une partie nulle est celle dite de l’appariement. Dans un jeu positionnel, si l’on parvient à construire un ensemble de paires de sommets de sorte que chaque sommet soit dans au plus une paire et que chaque ensemble gagnant intersecte les deux sommets d’une même paire, alors on dit qu’on a réussi à construire un appariement.

Par exemple, dans le jeu \(M(5,5)\) ci-dessous, il existe un appariement de \(24\) sommets avec \(12\) paires marquées de \(A\) à \(L\). Ainsi, les deux cases marquées \(B\) intersectent l’ensemble gagnant correspondant à la première ligne.

Chaque ensemble gagnant contient deux lettres identiques.

Lorsqu’un appariement existe, la stratégie de Xavier est alors la suivante : à chaque coup d’Olivia dans une paire, Xavier répond en jouant l’autre sommet de la paire. De cette façon, l’ensemble gagnant qui intersecte cette paire ne sera jamais remporté par Olivia puisque Xavier a joué dedans. En faisant cela pour chaque paire, et comme chaque ensemble gagnant est couvert par une paire, Xavier assurera bien le match nul. Notons au passage qui si Olivia ne joue pas un sommet d’une paire, Xavier peut répondre en jouant au hasard puisque cela n’impactera pas la stratégie globale.

Par définition, l’existence d’un appariement nécessite que le nombre d’ensembles gagnants ne soit pas trop grand par rapport au nombre de sommets (au plus la moitié). Dans l’exemple de \(M(5,5)\), il y a \(25\) sommets et \(12\) ensembles gagnants, ce qui permet d’espérer avoir un découpage en paires comme sur l’illustration. En revanche, si l’on considère par exemple \(M(4,4)\) avec \(16\) sommets et \(10\) ensembles gagnants, un tel appariement n’est pas possible. Cependant, il est parfois envisageable de le faire apparaître après un ou plusieurs tours de jeu (après avoir éliminé tous les ensembles gagnants touchés par Xavier lors de ses premiers coups). C’est ce que l’on a fait pour la stratégie du \(H\) précédemment.

Comparaison

Ces stratégies ont toutes les deux leurs avantages et leurs inconvénients. La stratégie du danger a l’avantage de pouvoir être calculée facilement : on peut calculer le danger de manière assez rapide avec un ordinateur. Trouver le coup qui diminue le plus le danger nécessite simplement pour chaque sommet de calculer la somme des dangers de chaque ensemble contenant ce sommet. Par contre, pour la stratégie par appariement, il faut trouver un appariement entre les sommets, ce qui est en général un problème compliqué pour un ordinateur.

Par contre, la stratégie par appariement a l’avantage d’être explicite : une fois l’appariement donné, on sait exactement où jouer chaque coup, il n’y a plus aucun calcul à faire et on sait où l’on va jouer. Ce n’est pas le cas de la stratégie par danger, pour laquelle on doit recalculer à chaque fois quel est le prochain sommet à jouer.

Enfin, la stratégie du danger a l’inconvénient de ne pas prendre en compte la structure du jeu, c’est-à-dire comment les ensembles gagnants s’intersectent. Considérons par exemple les deux jeux positionnels ci-dessous, ils ont la même valeur de danger (\(1.25\)), mais n’ont pas la même issue : la notion de danger ne prend par exemple pas en considération le fait qu’un sommet soit dans beaucoup d’ensembles gagnants. Les chercheurs du domaine essaient d’affiner le théorème d’Erdös-Selfridge pour y intégrer cela.

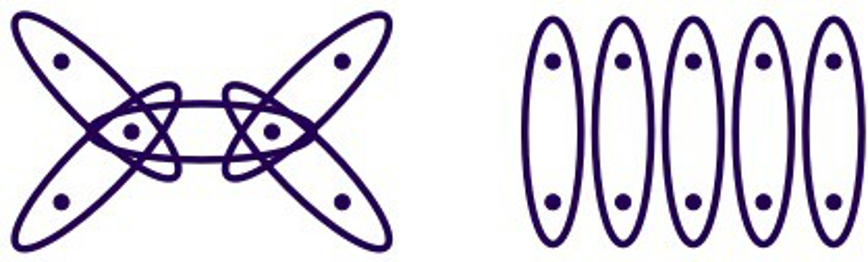
Deux jeux positionnels avec la même valeur de danger mais pas la même issue : Olivia gagne à gauche, c’est une partie nulle à droite.

Dans tous les cas, ces deux stratégies ne s’appliquent que dans des cas précis. Pour un jeu quelconque, il faudra la plupart du temps faire appel à d’autres stratégies. Elles restent tout de même utiles pour les fins de partie ou comme base pour d’autres stratégies.

Conclusion

Le morpion sous ses airs anodins est une porte d’entrée vers une collection de jeux dont la résolution est loin d’être évidente. Ainsi il suffit d’agrandir un peu la grille et le nombre symboles à aligner pour trouver des jeux non résolus à l’heure actuelle ! De plus, en considérant la famille plus générale des jeux positionnels, on découvre une communauté scientifique très active aujourd’hui qui cherche à répondre à des problèmes ouverts depuis longtemps. C’est le cas par exemple des jeux positionnels où tous les ensembles gagnants sont de taille au plus \(4\), pour lesquels on ne sait pas s’il est possible de construire des algorithmes de résolution efficaces.

Les animations présentes dans cet article ont été réalisées par Guillaume Bagan, sous la coordination des auteurs.