
Le nombre Pi est partout
Une première version de cet article est parue dans la rubrique « Logique et calcul » de la revue Pour la Science, n°464, en juin 2016.
L’ubiquité est « le fait d’être présent partout à la fois ou en plusieurs lieux en même temps. » De tous les nombres, π est celui qui jouit le plus spectaculairement de cette propriété : on le rencontre sans cesse en mathématiques et en physique. L’une des conséquences de cette ubiquité est qu’on découvre encore de nouvelles façons de calculer π. Il est devenu difficile de battre les formules qui évaluent très vite ce nombre, parce que les meilleures méthodes connues résultent de recherches approfondies, qu’elles sont d’une grande subtilité, et qu’elles sont d’une époustouflante efficacité.
Aujourd’hui, le record de calcul donne 22 459 milliards de décimales de π (voir les derniers records) et se fonde sur plusieurs formules, telle celle-ci, due aux frères David et Gregory Chudnowsky : le record de calcul donne
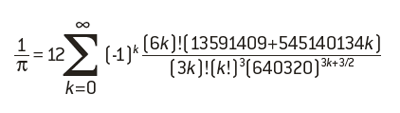
Bien que ne pouvant entrer en concurrence avec cette extraordinaire formule (en se limitant au terme k = 0, on trouve π = 3,1415926535897342…, ce qui est correct jusqu’au 14e chiffre), nous allons, pour le défi, la beauté ou même l’amusement et l’étonnement, présenter quelques-unes des étranges nouvelles méthodes de calcul de π.
Commençons par les méthodes utilisant des procédés physiques. La méthode de Monte-Carlo pour calculer π se fonde sur un principe très simple : la surface d’un disque de rayon r est πr2. Elle permet d’obtenir expérimentalement quelques décimales de π. On fait tomber au hasard des grains de sable sur un carré de côté r ; si les grains le recouvrent uniformément, la proportion de grains tombés dans le quart de disque de rayon r donne une valeur approchée de π/4 : la superficie du carré est r2, celle du quart de disque est πr2/4, donc le rapport est π/4 (voir l’encadré ci-après).
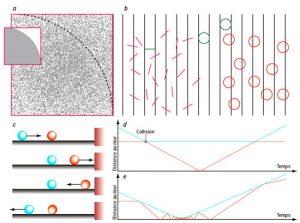
En comptant les points ou grains de sable supposés uniformément étalés sur un quart de disque inscrit dans un carré (a), et en faisant le rapport entre le nombre obtenu et le nombre total de grains de sable dans le carré, on obtient une valeur approchée de π/4. Lorsque les points sont choisis par des méthodes numériques (en utilisant par exemple des générateurs de nombres pseudoaléatoires), on parle de méthode de Monte-Carlo.
Si la répartition des points n’est pas uniforme, la méthode ne marche plus : il faut opérer un ajustement statistique. Vincent Dumoulin et Félix Thouin, plutôt que des grains de sable, ont tiré au fusil sur une cible. Le résultat de ce calcul agressif de π est 3,131.
Une deuxième méthode (b) est la méthode du naturaliste Buffon. Si on lance une aiguille aléatoirement sur un tracé constitué de droites parallèles espacées de la longueur L d’une aiguille, la probabilité de l’intersection d’une aiguille avec une droite est 2/π : en lançant beaucoup d’aiguilles et en comptant la proportion d’intersections, on en tire une approximation de π. Afin de comprendre cela, supposons que, en moyenne, le nombre de points d’intersection d’une courbe quelconque avec les droites soit proportionnel à sa longueur. Pour un cercle de diamètre L, ce nombre est toujours égal à 2 ; alors le nombre de points d’intersection pour l’aiguille sera en moyenne 2L/πL = 2/π.
Une troisième méthode exploite les chocs entre billes. Prenons une bille bleue et une bille rouge de même masse (c). La bille rouge est immobile. La bille bleue la frappe selon un choc élastique. La bille bleue s’immobilise et la bille rouge se trouve précipitée sur un mur où elle rebondit et repart vers la bille bleue. Après le choc, la bille rouge est à nouveau immobile et la bille bleue s’éloigne indéfiniment. Il y a eu 3 chocs : 3 est le premier chiffre de π (d).
Si les masses sont dans un rapport 100, au lieu de 3 chocs, il y en a 31 (e). Plus généralement, Gregory Galperin a prouvé que si le rapport des masses est 100n, alors le nombre de chocs reste fini, et c’est l’entier correspondant aux n + 1 premières décimales de π. Ainsi, pour n = 5, on aura 314 159 chocs : ce sont les 6 premiers chiffres de π.
Si par exemple on lâche 1 000 grains de sable et qu’il y en a 780 qui tombent dans le quart de disque, cela donne l’approximation
π = 4 × 780/1 000 = 3,12. En pratique, cette méthode souffre d’un grave défaut : elle suppose que l’on sache disposer des grains de sable uniformément sur le carré. Or en les lançant vers le centre, par exemple, les grains de sable auront une distribution plus dense vers le centre et plus éparse sur les bords. Le calcul sera faussé !
Il existe cependant des méthodes statistiques permettant de corriger cette non-uniformité. L’une d’elles consiste à compter le nombre de grains en affectant à chaque grain P un coefficient inversement proportionnel au nombre de grains situés dans un petit cercle autour de P. Les grains situés dans une zone dense sont ainsi comptés moins, ce qui corrige la non-uniformité.
Vincent Dumoulin et Félix Thouin, de l’université de Montréal, ont utilisé une méthode de ce type en tirant sur une cible distante de 20 mètres avec un fusil. Les expérimentateurs ont ainsi créé 30 857 trous dans la cible. Le calcul, avec correction de la non-uniformité, a donné π = 3,131, ce qui correspond à une erreur de 0,3 %.
La méthode des aiguilles de Buffon est un autre moyen de tirer de la physique des valeurs approchées de π. On lance n aiguilles de longueur L, sur un parquet dont la largeur des lattes est L ; on compte le nombre k d’aiguilles coupant les lignes parallèles de jonction entre lattes ; le quotient 2n/k est une valeur approchée de π. Cette méthode est très classique aussi nous n’y reviendrons pas. D’ailleurs, comme celle des coups de fusil, elle ne donnera jamais plus de quatre décimales exactes de π.
Le nombre de chocs avec deux billes et un mur
Plus intéressante et surprenante est la méthode physique proposée par Gregory Galperin, de l’université de l’Illinois. Elle n’utilise que des chocs entre billes qui suivent les lois de la physique classique et produisent les décimales de π les unes après les autres. Non seulement le dispositif imaginé donne π, mais il le donne écrit en base 10, et cela sans qu’aucun calculateur mécanique ou électronique ne soit mêlé à l’affaire.
Par rapport à celle de Buffon et du fusil, la méthode de Galperin a l’avantage que le hasard n’intervient pas et que le procédé déterministe de calcul de π donne donc, non pas une approximation de π, mais exactement les premiers chiffres de π… pour peu que le dispositif matériel soit exactement conforme au modèle théorique.
Pour comprendre cette méthode, commençons par le cas le plus simple. On considère deux billes A et B de même masse exactement (en fait, des masses ponctuelles, la rondeur des billes ne joue aucun rôle). La bille A est immobile à une distance L d’un mur plat M. On lance la bille B perpendiculairement au mur M dans la direction de A. Elle cogne la bille A de façon parfaitement élastique (conservation de l’énergie cinétique et de la quantité de mouvement). La bille B s’immobilise donc, et A part vers le mur M avec la vitesse qu’avait B et qu’elle lui a transmise. La bille A cogne le mur. On suppose à nouveau que le choc est parfaitement élastique. Elle rebondit, et repart vers B, toujours avec la même vitesse. La bille A cogne B, A s’immobilise et B repart en s’éloignant du mur indéfiniment. On suppose qu’il n’y a pas de frottement. Il y a eu trois chocs : deux entre les billes A et B et un entre la bille A et le mur. Le chiffre 3 est le premier de π. Ce n’est pas un hasard !
Si maintenant on refait l’expérience avec une bille B dont la masse est 100 fois celle de A (toujours en supposant des chocs parfaitement élastiques), le schéma des collisions est plus compliqué. Avant que B et A ne se séparent définitivement, le nombre de chocs entre A et B et de la bille A avec le mur est 31. Ce sont les deux premiers chiffres décimaux de π. Plus généralement, si le rapport des masses entre B et A est 102n, alors le nombre de chocs donnera exactement les n + 1 premiers chiffres décimaux de π. Ainsi, pour un rapport de masse de 10 000, il y a 314 chocs ; pour un rapport 1 000 000, il y a 3 141 chocs ; etc.
Une belle méthode, mais sans intérêt pratique
Pour les premières valeurs de n, on peut écrire de petits programmes qui confirment les affirmations indiquées. Le résultat général est cependant démontré de manière parfaitement rigoureuse (voir la bibliographie). Il nécessite juste une petite hypothèse : les 2n premiers chiffres de π ne doivent pas se terminer par n – 1 fois le chiffre 9. On sait que c’est vrai pour n plus petit que 11 229 000 000 000, puisqu’on connaît explicitement les décimales de π, mais pour n tendant vers l’infini, nul ne sait le démontrer. Cette propriété est jugée plus que probable, mais elle reste inaccessible à nos techniques de preuve.
La méthode est magnifique et a étonné les spécialistes des systèmes dynamiques, qui n’imaginaient pas que π soit présent dans des dispositifs aussi élémentaires.
Sur le plan pratique, la méthode est cependant d’un intérêt limité. Comment ajuster les masses de A et de B avec la précision exigée ? On ne peut espérer faire beaucoup plus que le nombre d’Avogadro, soit environ 1024, ce qui ne donnera que 12 décimales, et les autres mesures sont à l’avenant. Comment être certain de lancer les billes perpendiculairement au mur avec toute l’exactitude nécessaire ? Comment s’assurer que les chocs soient parfaitement élastiques et qu’il n’y ait aucun frottement ?
Pas plus que la méthode de Buffon ou du fusil, dont on ne tire jamais plus de quatre décimales de π, on ne tirera de celle de Galperin un grand nombre de chiffres de π. Si l’on veut s’en tenir à des méthodes physiques, le mieux est peut-être simplement de mesurer avec soin le périmètre et le diamètre d’un cercle assez grand et de faire le quotient. En réalité, rien ne vaut les calculs purs ne s’appuyant pas sur des hypothèses et des mesures physiques qu’on ne parvient jamais à mener avec plus de quelques chiffres significatifs. Venons-en donc aux méthodes mathématiques.
Nombre d’Archimède et conjecture de Syracuse
Le nombre π, dont Archimède a été le premier à proposer une méthode mathématique permettant d’en calculer les chiffres aussi loin qu’on le souhaite, porte parfois le nom de constante d’Archimède. Archimède est né, a vécu et est mort à Syracuse, en Sicile. En mathématiques, Syracuse est aussi le nom d’une conjecture qui intéresse beaucoup de monde à cause de sa simplicité.
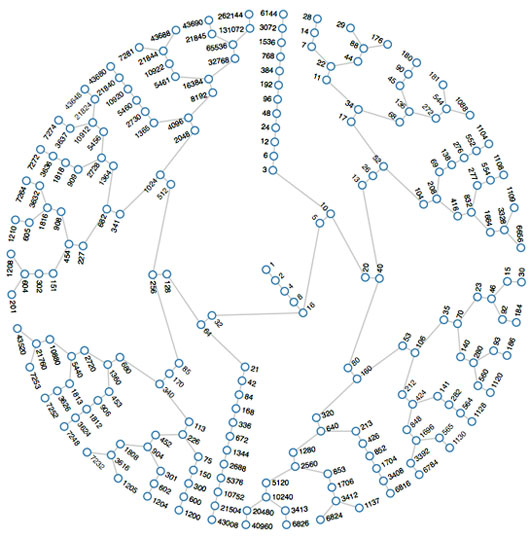
Source de l’image, site de Jason Davies.
Décrivons cette « conjecture de Syracuse » ou « conjecture de Collatz ». On part d’un entier positif quelconque n ; s’il est pair, on le divise par 2 ; s’il est impair, on le remplace par 3n 1. Et on recommence. Par exemple, de n = 13 on passe à 40, puis à 20, 10, 5, 16, 8, 4, 2 et enfin 1. La conjecture affirme que quel que soit l’entier initial n, on finit toujours par arriver à 1. Personne n’a su la démontrer. Expérimentalement, elle a été vérifiée jusqu’à 260 = 1,15 × 1018. A priori, elle n’a rien à voir avec π, malgré son nom qui semble établir un lien avec Archimède. La Syracuse qui intervient dans le nom de la conjecture est en fait la ville américaine de Syracuse, dans l’État de New York, dont l’université a été le lieu d’une étape importante dans la diffusion de la conjecture au monde entier.
Une question naturelle se pose cependant : si π est vraiment partout, n’existe t-il pas un moyen de le calculer à partir de la conjecture de Syracuse ? La réponse est oui. Le Français Roland Yéléhada a en effet mis au point une méthode de calcul de π à partir de la conjecture de Syracuse.
La conjecture de Syracuse, dont le nom provient de l’université de Syracuse, aux États-Unis – laquelle a joué un rôle important dans sa popularisation – reste ouverte. Son énoncé est compréhensible par tous : « Quand on part d’un entier positif n quelconque et que, de manière répétée, on le divise par 2 s’il est pair et on le remplace par 3n + 1 s’il est impair, on finit toujours par tomber sur 1. »
Les mathématiciens n’ont pas trouvé de contre-exemple, en dépit de recherches intensives sur ordinateur. La conjecture a occupé dans les années 1980 tant de mathématiciens que, dans l’ambiance de la guerre froide, on a émis l’hypothèse que c’était une arme soviétique destinée à occuper à cette fadaise les mathématiques américaines. L’image ci-contre figure l’arbre reliant les nombres dont la longueur de la suite aboutissant à 1 est inférieure à 20.
Archimède (de Syracuse) fut le premier à proposer une méthode de calcul mathématique de π permettant d’en connaître autant de décimales qu’on veut. Étonnante coïncidence, on vient de proposer un lien entre la conjecture de Syracuse et le nombre π.
Le principe est le suivant. On calcule la suite de Syracuse pour tous les nombres jusqu’à une certaine borne n, par exemple 100. Pour chacune des suites calculées, par exemple [13, 40, 20, 10, 5, 16, 8, 4, 2, 1], on évalue la longueur, ici 10, et la somme des éléments de la suite, ici 119. On teste si les deux nombres obtenus ont un diviseur commun plus grand que 1 ; ce n’est ici pas le cas. On prend alors le nombre a de fois où la réponse a été non, puis on divise a par n, ce qui donne un nombre b. On calcule enfin la racine carrée de 6/b = c. Ce nombre c est une valeur approchée de π.
La méthode ne donne pas très rapidement les chiffres de π, mais on a des raisons de croire qu’elle converge vers π, car la longueur et la somme d’une suite de Syracuse, à cause de comportements imprévisibles des suites, sont comme deux nombres entiers tirés au hasard. Or on sait, d’après un résultat de 1881 démontré par Ernesto Cesaro, que la probabilité que deux entiers tirés au hasard n’aient pas de diviseur commun supérieur à 1 est 6/π2. Bien qu’aujourd’hui aucune preuve mathématique rigoureuse n’ait été donnée du résultat quand n tend vers l’infini, les expériences effectuées en écrivant de petits programmes confirment qu’il s’agit bien d’une méthode de calcul de π. Pour n = 100, on obtient a = 66, b = 0,66, c = 3,01511… Pour n = 1 000, on obtient a = 606, b = 0,606, c = 3,146583…
Bien évidemment, il s’agit d’un jeu et pour disposer de beaucoup de décimales de π, ce procédé n’est pas à recommander, pas plus que les méthodes de Buffon, du fusil ou de Galperin.
Voici à présent une méthode tout aussi étonnante que les précédentes, mais plus simple encore à mettre en œuvre et qui, elle, pourra plus rapidement donner jusqu’à 5 ou 6 décimales de π.
Caché dans une figure fractale

L’ensemble de Mandelbrot est la plus célèbre des fractales.
On part d’un point c (marqué en rouge) de coordonnées (–3/4, 1/10k) et on applique la règle cn + 1 = cn2 + c jusqu’à sortir du disque de rayon 2. Les coordonnées du « carré » c2 du point c = (a, b) sont, par définition, (a2 – b2, 2 ab).
Le nombre d’étapes nécessaires est 3 pour k = 0 ; 33 pour k = 1 ; 315 pour k = 2 ; 3 143 pour k = 3 ; 31 417 pour k = 4 ; 314 160 pour k = 5 ; 3 141 593 pour k = 6. On reconnaît (à l’exception des derniers chiffres) le développement décimal de π. La preuve précise que ces calculs des chiffres de π se poursuivent jusqu’à l’infini n’a été donnée qu’en 2001, par Aaron Klebanoff aux États-Unis : π est caché de manière inattendue dans l’ensemble fractal de Mandelbrot, qui est l’ensemble des points c ne s’échappant pas à l’infini.
Sa définition, succincte, tient en quelques mots : c’est l’ensemble des points c du plan complexe tels que la suite c0 = 0, c1 = c, c2 = c12 +c,…, cn + 1 = cn 2 + c,… reste dans une partie bornée du plan ; autrement dit, c’est l’ensemble des points c tels que la distance de cn à 0 ne tend pas vers l’infini quand n tend vers l’infini.
Si vous n’avez jamais entendu parler du « plan complexe », il suffit, pour comprendre tout ce qui nous occupe ici, de savoir que le carré d’un point de coordonnées (a, b) (représentant le nombre complexe c = a + ib) dans le plan complexe est le point de coordonnées (a2 – b2, 2ab).
Les outils nécessaires à la visualisation de l’ensemble de Mandelbrot, et surtout les puissances de calcul suffisantes (en chaque point il faut calculer la suite cn), ne sont devenus disponibles qu’au début des années 1980. Grâce à quoi on a pris conscience de la richesse de cet ensemble et du découpage infiniment fin de sa frontière. Adrien Douady, de l’université Paris-Sud, et John Hubbard, de l’université Cornell aux États-Unis, ont montré en 1981 que cet ensemble est connexe, c’est-à-dire d’un seul tenant : on peut passer d’un point à un autre de l’ensemble en utilisant un chemin qui y reste tout le temps.
En 1991, Dave Boll, étudiant en informatique à l’université d’État du Colorado, explore l’ensemble de Mandelbrot et tente de savoir si un point unique sépare la partie de cet ensemble à droite du point c = (– 3/4, 0) de la partie qui se trouve à sa gauche. Il prend donc des valeurs de c de plus en plus proches du point (– 3/4, 0) et calcule combien de points de la suite il faut considérer avant que cn sorte du cercle de rayon 2. On sait en effet que dès que la suite cn sort de ce cercle, elle part inévitablement à l’infini.
Il essaie donc comme point de départ c = (– 3/4, 1) et trouve que 3 itérations suffisent pour que la suite sorte du cercle. Il essaie c = (– 3/4, 1/10), il en faut maintenant 33. Avec c = (– 3/4, 1/100), il en faut 315. Avec c = (– 3/4, 1/1 000), il en faut 3 143. Avec c = (– 3/4, 1/10 000), il en faut 31 417. Avec c = (– 3/4, 1/100 000), il en faut 314 160. Avec c = (– 3/4, 1/1 000 000), il en faut 3 141 593. Etc.
Stupéfaction ! Les chiffres des nombres calculés sont, à l’exception des derniers, ceux de π écrit en base 10 : 314159… Les calculs à programmer si vous voulez contrôler les affirmations mentionnées sont particulièrement simples. Pour chaque entier k à partir de zéro, définissez la suite de couples de nombres réels (an, bn) :
a0 = 0, b0 = 0, a1 = – 3/4, b1 = 1/10k, an + 1 = an2 – bn2 – 3/4, bn + 1 = 2anbn + 1/10k et déterminez le premier n tel que an2 + bn2 soit supérieur à 4. Les nombres n calculés seront les nombres 3, 33, 315, 3 143, 31 417, 314 160, 3 141 593, etc.
David Boll découvre aussi que, partant de (1/4 + c, 0) et en prenant des valeurs de c de plus en plus petites (cette fois, il commence par c = 1/100 et divise par 100 à chaque nouvel essai), on tombe sur les entiers suivants : 30, 312, 3 140, 31 414, 314 157, etc. À nouveau, c’est π !
Notons que rien, dans la définition de l’ensemble de Mandelbrot, n’a de rapport avec la géométrie du cercle. Pourtant, une simple itération partant d’un nombre choisi de plus en plus petit donne assez rapidement des décimales de π.
Notons aussi que, par cette méthode, calculer 20 décimales de π demanderait plus de 1020 itérations, ce qui est la limite de ce qu’on peut espérer faire aujourd’hui, même en mobilisant les plus puissants ordinateurs. Cette méthode, aussi simple et élégante qu’elle soit, ne peut donc pas rivaliser avec les meilleures méthodes connues de calcul de π (mentionnées au tout début de cet article), qui sont plus compliquées mais beaucoup plus efficaces.
Écrit en diagonale par le jeu de la vie
Un exploit de calcul d’une autre nature concernant π est lié au célèbre « jeu de la vie » de John Conway.
Une fantastique configuration des cellules du jeu de la vie a été conçue par Adam Goucher. En respectant la règle unique de fonctionnement « Naissance si 3 voisins vivants, survie si 2 ou 3 voisins vivants », elle calcule π. Bien plus surprenant, elle écrit en diagonale le résultat sous la forme d’une configuration stable qui énumère les chiffres décimaux de π. On ne peut pas ici faire apparaître les détails de son million et quelque de cellules vivantes, mais vous pouvez la télécharger et la faire fonctionner avec le logiciel gratuit Golly.
Ce réseau d’automates cellulaires est l’un des moyens les plus élémentaires de mener des calculs. Chaque case du plan infini, muni d’un quadrillage, est occupée par un microcalculateur qui ne fait qu’une seule chose extrêmement simple :
– Si, à l’instant t, il est dans l’état mort (représenté par la couleur blanche), alors le microcalculateur examine ses 8 voisins ; si 3 exactement sont vivants, il passe dans l’état vivant à l’instant t 1 ; sinon, il reste dans l’état mort.
– Si, à l’instant t, il est dans l’état vivant (représenté par la couleur noire), alors le microcalculateur examine ses 8 voisins ; si 2 ou 3 sont dans l’état vivant, le calculateur reste dans l’état vivant à l’instant t 1 ; sinon, il meurt. En résumé : « Naissance si 3 voisins vivants, survie si 2 ou 3 ».
Le pouvoir de calcul d’un tel réseau est bien supérieur à ce que l’on peut imaginer, et d’ailleurs John Conway a montré qu’on pouvait calculer avec cet automate cellulaire tout ce qui est calculable par algorithme. Pour cela, il faut placer au départ la bonne configuration et ne pas être pressé !
En 2010, Adam Goucher, prenant au sérieux le résultat théorique de John Conway, a conçu une configuration du jeu de la vie comportant 1 389 325 cases vivantes. En évoluant génération après génération, la configuration calcule les chiffres de π écrit en base 10 et, c’est le plus étonnant, va les écrire en diagonale à l’aide de cases vivantes déposées qui dessinent les chiffres en écriture habituelle.
L’exploit est inouï, mais, une fois encore, c’est un jeu : au bout de plusieurs heures de fonctionnement avec mon ordinateur, la configuration d’Adam Goucher a réussi à écrire 3,14159265. L’obtention d’autres décimales demanderait des jours ou des semaines. Le calcul utilise un produit infini et progresse en O(n6), ce qui veut dire que s’il faut k heures de calcul pour avoir n décimales, en avoir le double demandera 26 = 64 fois plus de temps (et cela à la condition que la mémoire disponible sur l’ordinateur ne fasse pas défaut).
Pour terminer, signalons deux méthodes illusoires de calcul de π, parfois présentées comme sérieuses, mais qui en réalité ne vous donneront jamais rien.
La première pourrait être qualifiée de géographique. Dans un article publié dans la revue Science en mars 1996, Hans-Henrik Stølum, de l’université de Cambridge, décrit un modèle d’écoulement des cours d’eau. Il tire de son modèle l’affirmation qu’en moyenne, le rapport entre la longueur d’un fleuve et la distance à vol d’oiseau entre la source et l’endroit où le fleuve se jette à la mer est le nombre π. En se fondant sur ce résultat, on pourrait donc tenter de calculer π en prenant un grand nombre de fleuves, et en calculant la moyenne des rapports entre leur longueur et la distance parcourue à vol d’oiseau entre la source et l’embouchure.
Malheureusement, tous ceux qui, à partir de bases de données géographiques, ont essayé arrivent à des valeurs sensiblement plus petites que π. Il semble bien que le modèle théorique soit inexact, et qu’en tout cas, pour calculer π, on ne tirera rien de la longueur des fleuves.
π n’est tout de même pas partout !
L’autre méthode illusoire est celle liée à la théorie économique de Martin Armstrong. Cet Américain est l’auteur d’une théorie (Economic Confidence Model) selon laquelle l’économie est soumise à des ondes cycliques tous les 8,6 ans et que les prendre en compte permet de prévoir les crises. La durée de 8,6 ans correspond à 3 141 jours, soit 1 000 π. On a du mal à comprendre ce que π, avec une précision de 4 chiffres, vient faire dans les cycles économiques, mais Martin Armstrong prétend avoir annoncé, grâce à sa théorie, la crise de 1987 au jour près.
Plus récemment, Martin Armstrong avait annoncé une nouvelle crise pour le 1er octobre 2015. Elle ne s’est pas produite ! Tout cela ne semble pas très sérieux et, si les mathématiciens sont bien persuadés de l’importance et de l’ubiquité de π, ils n’ont pas la naïveté de croire en de telles théories dont, d’ailleurs, aucune justification n’est présentée. C’est un plaisir de jouer avec π et de le découvrir partout, mais c’est avant tout un amusement qu’il est sage de ne pas transformer en superstition numérologique.
Quelques références vous sont proposées pour en savoir plus sur le nombre π.
- V. Dumoulin et F. Thouin, A ballistic Monte Carlo approximation of π, prépublication arXiv:1404.1499, 2014.
- G. Galperin, Playing pool with π (the number π from a billiard point of view), Regular and Chaotic Dynamics, vol. 8(4), pp. 375-394, 2003.
- A. Klebanoff, π in the Mandelbrot set, Fractals, vol. 9(4), pp. 393-402, 2001.
- H.-H. Stølum, River meandering as a self-organization process, Science, vol. 271, pp. 1710-1713, 1996.
- Dessin animé montrant les 31 chocs de deux billes dont le rapport des masses est 100, 2016 : https://www.youtube.com/watch?v=4UhPTrHIprk
- Wikipédia, Aiguille de Buffon, consulté en 2016 : https://fr.wikipedia.org/wiki/Aiguille_de_Buffon
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).