
Le plus court chemin
Heureusement, il existe des algorithmes qui évitent d'avoir à calculer tous les trajets possibles. Pour cela, ils mettent en œuvre diverses stratégies.
1. Un problème moins simple qu’il n’y paraît
Un problème vite inextricable
On représente un réseau par un graphe composé de nœuds (les sommets du graphe) et de liens orientés (les arcs du graphe). Imaginez, par exemple, un réseau composé de 20 nœuds – ce qui est très raisonnable – et comportant un lien direct entre chaque nœud (soit 380 liens orientés). Un simple calcul combinatoire montre qu’entre deux nœuds donnés, le nombre de « chemins » possibles est supérieur à 6000 milliards !
Entre deux nœuds donnés, le nombre de chemins possibles est supérieur à factorielle 18.
En effet, rien que pour les trajets passant par les 20 sommets, soit 19 liens directs, il y a 18 ! chemins.
Ainsi, à supposer qu’il faille 1 microseconde pour calculer la longueur d’un trajet, la solution exhaustive prendrait environ 6 milliards de secondes, c’est-à-dire plus de 740 000 jours… et même si on réduisait le temps de calcul d’un trajet à 1 nanoseconde, il faudrait encore 741 jours. Cet exemple est extrême, mais il montre bien la nécessité de disposer d’algorithmes évitant de calculer tous les trajets possibles, pour éviter l’« explosion combinatoire ». Heureusement, on connaît de tels algorithmes, dont les temps de calculs resteront proportionnels, dans le pire des cas, au cube du nombre de nœuds (et souvent au carré). Ainsi, pour notre exemple, le nombre de chemins calculés sera au pire de 203 c’est à dire 8000 ou même de 202 c’est-à-dire 400, selon les cas. Ce qui est nettement mieux, chacun en conviendra.
Un cas particulier d’un problème plus général
Le problème sous-jacent est celui du « chemin de valeur optimale (ou de meilleure valeur) dans un graphe valué ». L’exemple le plus connu est sans doute celui du réseau de communication : il est composé de nœuds et de liens, en général orientés, chaque lien reliant directement un nœud origine à un nœud extrémité. On imagine aisément la diversité du type de valeurs pouvant être attribuées aux liens : distances, temps (de parcours), coûts (de transferts), fiabilités (valeurs comprises entre 0 et 1), capacités (débits maximum, par exemple en kb/s), etc. Le long d’un chemin, les distances, temps, coûts vont en général s’additionner, les fiabilités vont se multiplier, les capacités vont se composer par minimum, et l’on aura tendance à rechercher un minimum dans le cas des distances, temps, coûts, mais un maximum dans le cas des fiabilités ou des capacités.
On imagine aisément toutes les applications d’un tel mécanisme : étude d’un itinéraire routier, organisation d’un réseau de télécommunication, système d’information de trafic d’un réseau ferroviaire, analyse de réseaux sémantiques (par exemple de citations bibliographiques), etc.
L’étude de ce problème générique nécessite une présentation formelle qui fait appel à des notions algébriques avancées.
Un dioïde est un ensemble E muni de deux lois de composition interne, notées ⊕ et ⊗, telles que :
- ⊕ est associative, commutative et possède un élément neutre α,
- ⊗ est associative, possède un élément neutre e, et est distributive à gauche et à droite par rapport à ⊕,
- α est élément absorbant de ⊗.
Un exemple de dioïde – utilisé pour la recherche du plus court chemin – est l’ensemble des nombres réels auquel est ajouté l’élément +∞; avec pour première loi de composition ⊕ le minimum dont l’élément neutre est α=+∞ et pour deuxième loi de composition ⊗ l’addition dont l’élément neutre est e=0.
Nous avons choisi de nous limiter ici au problème de recherche du « plus court chemin », que nous préférons appeler « chemin de valeur additive minimale ».
Le terme « chemin de valeur additive minimale » montre bien comment le problème du plus court chemin se rattache au problème général du chemin de valeur optimale. Ici, les valeurs des arcs sont des nombres réels (de signe quelconque), elles se composent par addition, et se comparent au sens du minimum.
Pour s’appliquer à un autre problème, les algorithmes obtenus dans ce contexte peuvent aisément se transformer en changeant la loi de composition des valeurs et l’opérateur de comparaison. Par exemple, un autre problème intéressant est celui du chemin le plus fiable.
Les valeurs des arcs sont des fiabilités (ou probabilités d’existence), nombres réels compris entre 0 et 1. Si deux sommets A et B sont reliés par un arc de fiabilité 0,9, par exemple, cela signifie que ce lien direct a 9 chances sur 10 d’être opérationnel.
Le long d’un chemin, les fiabilités se multiplient, et on compare selon le maximum. Toute opération d’addition de valeurs sera remplacée par une multiplication, et tout test ≤ sera remplacé par le test ≥, min sera remplacé par max, 0 sera remplacé par 1, etc.
Mieux formaliser le problème pour le résoudre plus efficacement
Précisons maintenant le problème. Nous en distinguons trois types :
- plus court chemin entre deux sommets donnés ;
- plus courts chemins d’origine fixée mais vers n’importe quelle extrémité ;
- plus courts chemins de n’importe quelle origine vers n’importe quelle extrémité.
À première vue, il semble que ces problèmes aillent du plus simple au plus complexe. En effet, le nombre de chemins à déterminer augmente. Cependant, et contrairement à l’intuition précédente, la résolution du problème (1) nécessite en général de résoudre le problème (2) ! De plus, dans le cas général, où les valeurs des liens peuvent être négatives, le meilleur algorithme connu pour résoudre le problème (3) ne demande pas plus d’opérations que le meilleur algorithme connu du problème (2). C’est pourquoi nous nous focaliserons sur cet algorithme, celui de Roy-Warshall-Floyd.
Il convient de préciser aussi ce que l’on cherche à déterminer : le premier résultat cherché est bien sûr la valeur minimale (pour chaque couple de sommets considéré).
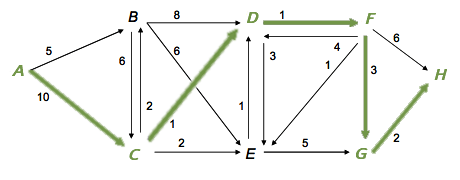
Meilleur chemin de A à H.
Par exemple, dans le graphe représenté sur cette figure, le meilleur chemin pour aller de A à H a pour valeur 17. Mais souvent cela ne suffit pas : s’il est bien de connaître la meilleure valeur possible, il est encore mieux de connaître le tracé d’un chemin ayant cette valeur. Ainsi, le meilleur chemin de A à H a pour valeur 17, et son tracé est A;C;D;F;G;H. On parle alors de routage.
Le problème étant ainsi précisé, peut-on affirmer qu’il y a toujours une solution ? La question peut paraître triviale, mais elle ne l’est pas. Supposons que les valeurs des arcs soient de signe quelconque, et que ces valeurs s’additionnent le long des chemins. Si le graphe possède des circuits, c’est-à-dire des chemins permettant de revenir au point de départ, il peut exister des chemins empruntant de tels circuits.
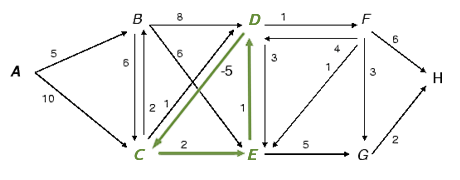
Graphe avec circuit absorbant.
Sur cette figure, par exemple, le chemin A;B;D;C;E;D;F;G;H comprend le circuit D;C;E;D. Dans cet exemple, le circuit D;C;E;D a pour valeur -2, qui est <0. Si l’on cherche les chemins de valeur minimale entre A et H, le problème n’a pas de solution. En effet, le chemin A;B;D;F;G;H vaut 19. Le chemin A;B;D;C;E;D;F;G;H est meilleur (valeur 17). Le chemin A;B;D;C;E;D;C;E;D;F;G;H, faisant deux tours, est encore meilleur (valeur 15). Et ainsi de suite : on peut trouver un chemin de valeur aussi petite que l’on veut, en « tournant » suffisamment de fois sur le circuit ! De tels circuits s’appellent circuits absorbants, et leur présence éventuelle doit être détectée par les algorithmes, qui sinon risqueraient de « boucler » indéfiniment. La question n’est pas seulement théorique, car il existe des applications concrètes où les graphes peuvent avoir des circuits dont la valeur est de signe quelconque. C’est le cas par exemple pour les problèmes d’ordonnancement (ou plannings), qui nécessitent le calcul de chemins de valeur maximale.
Les problèmes d’ordonnancement mettent en jeu des tâches ayant une durée donnée, et soumises à des contraintes temporelles. Par exemple, « telle tâche ne peut commencer avant que telle autre soit terminée ». Il s’agit alors de déterminer un « ordonnancement compatible », autrement dit un calendrier d’exécution des tâches, respectant les durées et les contraintes, et satisfaisant à certaines exigences comme, par exemple, se terminer au plus vite. Les données d’un tel problème peuvent être modélisées par un graphe, appelé « potentiel-tâche », où chaque sommet représente une tâche et chaque arc représente une contrainte. Selon la nature de la contrainte (« au plus tôt », « au plus tard », « synchronisation », etc.), la valeur attribuée à l’arc pourra être positive ou négative. La résolution d’un problème d’ordonnancement revient alors à déterminer des chemins de valeur maximale dans le graphe potentiel-tâche.
Différentes stratégies algorithmiques
Si on s’intéresse uniquement à trouver le meilleur chemin issu d’un sommet donné, il existe des algorithmes assez simples et répandus dans lesquels, par construction, il ne peut pas y avoir de circuits absorbants.
L’algorithme ordinal repose sur le principe très simple d’exploration à partir des prédécesseurs, en supposant qu’il n’y a pas de circuit, et que le sommet de départ est le seul sommet sans prédécesseur.
L’algorithme ordinal est une mise en œuvre simplifiée de l’algorithme plus général de Bellman-Kalaba. Il repose sur le principe très simple d’exploration à partir des prédécesseurs. Un sommet y pour lequel la valeur m(y) et un prédécesseur p(y) ont été calculés est dit calculé. On constate que, si tous les prédécesseurs d’un sommet x ont été calculés, alors on peut calculer x : sa valeur est m(x) = min(m(y) + v(y, x)) où y est prédécesseur de x – v(y, x) désignant la valeur de l’arc (y, x), et p(x) est un prédécesseur de x pour lequel ce minimum est atteint. Initialement, on calcule A (m(A) = 0, p(A) non défini – puisque c’est l’origine). Ensuite, tant qu’il reste des sommets non calculés, on en sélectionne un dont tous les prédécesseurs sont calculés (ceci est toujours possible car le graphe est sans circuit) et on le calcule.
/*Initialisations */
a_calculer = X-{A} ; /* ensemble des sommets du graphe, sauf A*/
m(A)=0 ;
/* Itérations */
tant que a_calculer=∅
soit x ∈ a_calculer tel que tous les prédécesseurs de x sont calculés ;
m(x)=min(m(y)+v(y,x)|y est prédécesseur de x), atteint pour p(x) ;
a_calculer=a_calculer-{x} ;
ftantque
La complexité de l’algorithme est de l’ordre de n2. En effet, s’il y a n sommets, l’algorithme nécessite exactement n – 1 étapes. À l’étape k, on recherche (dans a_calculer, de cardinal n – k) un sommet candidat, puis on calcule un minimum sur au plus k éléments, c’est-à-dire au pire n – k + k = n opérations. Il y a donc, en tout, au pire n2 opérations.
L’algorithme de Dijkstra quant à lui repose sur le principe d’« exploration à partir du meilleur », c’est à dire du meilleur prédécesseur visité. Il peut être utilisé quand tous les arcs ont une valeur non négative, correspondant à ce qui est consommé sur un trajet donné. Dans ce cas, il ne peut pas y avoir de circuits absorbants, mais il peut y avoir d’autres types de circuits, comme des liens bidirectionnels. En pratique, cet algorithme est très souvent utilisé pour résoudre des problèmes de routage dans les réseaux de télécommunication.
Ces deux algorithmes peuvent se substituer à un algorithme plus général, l’algorithme de Bellman-Kalaba (connu aussi comme Bellman-Ford). Cet algorithme ne présuppose pas l’absence de circuits absorbants sur le graphe, et peut détecter et signaler ces circuits éventuels. Il s’appuie sur un des principaux principes d’optimisation combinatoire : le principe de la programmation dynamique, formulé à l’origine par Bellman et Kalaba.
Cet algorithme date de la fin des années cinquante, c’est l’un des nombreux exemples d’application d’une méthode d’optimisation plus générale conçue quelques années plus tôt par Richard Bellman, la programmation dynamique.
Appelons longueur d’un chemin le nombre d’arcs qui composent ce chemin (attention de ne pas confondre longueur et valeur !). Le principe de programmation dynamique s’exprime ici de la manière suivante : on résout séquentiellement les problèmes P(k), où P(k) détermine les chemins de valeur minimum issus de A, de longueur ≤ k.
Soit u un chemin allant de A à un sommet x, de longueur l ≤ k, et y le prédécesseur de x sur ce chemin. Le sous-chemin u’, allant de A à y, est de longueur l– 1 ≤ k – 1. Si u est optimal, alors u’ l’est aussi. Si on note, pour tout entier k ≥ 1 et tout sommet x, m(x, k) la valeur minimum des chemins de A à x, de longueur ≤ k, (+∞ si de tels chemins n’existent pas), alors m(x, k) = min(m(y, k – 1) + v(y, x)) où le minimum est pris sur l’ensemble des y prédécesseurs de x. Ainsi, ayant résolu le problème P(k – 1), on peut résoudre P(k).
La résolution de P(1) est triviale, puisqu’un chemin de longueur ≤1 se réduit à un arc : pour tout x, m(x, 1) = v(A, x) si x est successeur de A (l’arc (A, x) existe), +∞ sinon.
Quand arrêter le calcul ? Deux situations sont possibles : Soit on atteint la stabilité (c’est-à-dire, il existe un k tel que, pour tout x, m(x, k) = m(x, k – 1). On a alors m(x, k) = m(x). Cette situation se produira nécessairement, avec k ≤ n (où n est le nombre de sommets du graphe) si le graphe n’a pas de circuit absorbant. La deuxième situation se produit lorsqu’il y a des circuits absorbants : le calcul n’est pas stabilisé à l’étape n, il faut alors l’arrêter (sinon il continuerait indéfiniment). On voit que, dans tous les cas, l’algorithme s’arrête après un nombre fini (≤ n) d’étapes.
/* Initialisations */
m(A)=0 ;
pour tout sommet x
si x est successeur de A
m(x)=v(A,x) ;
p(x)=A ;
sinon m(x)=+∞;
fsi
k=1 ; stabilité :=faux ;
/* Itérations *
/ jusqua stabilité
ou k=n
stabilité=vrai ;
pour tout sommet x
pour tout sommet y prédécesseur de x
si m(y)+v(y,x) < m(x)
m(x)=m(y)+v(y,x) ;
p(x)=y ;
stabilité=faux ;
fsi
fpour
fpour
k=k+1
fjusqua
si stabilité=faux alors "il y a des circuits absorbants" fsi
L’algorithme effectue au plus n étapes. À chaque étape, la valeur de chaque sommet est mise à jour en calculant un minimum sur l’ensemble des prédécesseurs du sommet (dont le cardinal est au plus égal à n – 1). Il y a donc, au pire, n × n × n = n3 opérations élémentaires.
Ces trois mécanismes peuvent être considérés comme des algorithmes d’exploration de la descendance du sommet, avec des stratégies différentes : tous les prédécesseurs calculés pour l’algorithme ordinal ; le meilleur visité, pour celui de Dijkstra ; et enfin par longueur successive pour celui de Bellman-Kalaba. Les deux premiers ont une complexité plus faible (de l’ordre de n2 dans le pire cas) au lieu d’être de l’ordre de n3 pour le dernier, tout comme pour l’algorithme de Roy-Warshall-Floyd. Ils sont donc utiles dans des situations où il y a un très grand nombre de sommets. C’est le cas par exemple des grands réseaux, des réseaux sémantiques (moteurs de recherche), ou encore des systèmes de recherche d’horaires. Ainsi, un graphe modélisant le système horaire des chemins de fer allemands comprend de l’ordre de 1 million de sommets et 1 million et demi d’arcs.
De plus, pour l’algorithme ordinal ou celui de Dijkstra, chaque étape nous fournit la valeur définitive d’un sommet, et on le sait. Si on s’intéresse aux chemins de valeur minimale entre le sommet de départ A et un sommet particulier B, on peut arrêter le calcul dès que B est calculé, même si tous les sommets ne sont pas calculés. On dit que la stratégie est gloutonne, ce qui signifie que certains résultats ne seront plus remis en question (un glouton est quelqu’un qui avale et ne peut pas revenir en arrière, c’est-à-dire ne peut pas remettre en cause ce qu’il vient de faire).
Pour l’algorithme de Bellman-Kalaba ou celui de Roy-Warshall-Floyd, en revanche, aucun sommet ne peut être considéré comme calculé avant que tous les sommets soient calculés : jusqu’à la fin de l’exécution (c’est-à-dire jusqu’à ce que la stabilité soit atteinte), toute valeur est susceptible d’être modifiée. Il s’agit là d’une stratégie de point fixe. Ce sont deux stratégies algorithmiques très générales que l’on rencontre ici.
2. Trouver les chemins issus d’un sommet : l’algorithme de Dijkstra
Cet algorithme est dû à Edsger W. Dijkstra (1930-2002), qui est l’un des trois ou quatre informaticiens les plus importants du XXe siècle : il reçut, en 1972, le prestigieux Turing Award, équivalent du Prix Nobel ou de la médaille Fields. Il publia l’algorithme décrit ici en 1959 (« A Note on Two Problems in Connexion with Graphs », Numerische Mathematik, vol.1, PP. 269-271, 1959), l’année où il soutint sa thèse à l’université d’Amsterdam. Un excellent article (en anglais), téléchargeable en PDF, résume ses nombreuses contributions.
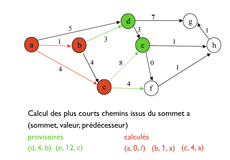
Un exemple de déroulement de l’algorithme de Dijkstra.
Principe de l’algorithme
Pour chaque sommet x, on veut calculer la valeur minimum m(x) des chemins allant du sommet de départ A à x. Pour le routage, on veut déterminer le prédécesseur de x, noté p(x), sur un chemin de valeur m(x). Ceci permet de « tracer », en le « remontant », le meilleur chemin du sommet de départ A à n’importe quel sommet x.
L’algorithme de Dijkstra repose sur le principe d’« exploration à partir du meilleur », c’est à dire du meilleur prédécesseur visité.
Cette animation Flash présente un exemple de déroulement de l’algorithme de Dijkstra. Pour la visionner, Adobe Flash Player est nécessaire.
Un sommet x est dit visité si au moins un chemin de A à x a été évalué ; un sommet visité possède des valeurs m(x), p(x) provisoires : m(x) est la valeur minimum des chemins de A à x déjà évalués, et p(x) le prédécesseur correspondant.
Un sommet est dit calculé s’il est visité et si l’on sait que ses valeurs m(x), p(x) sont définitives (et correctes).
Initialement, bien sûr, le sommet A est calculé (avec m(A) = 0, p(A) non défini puisque A est le point de départ des chemins), et chaque successeur x de A est visité, avec m(x) = v(A, x), p(x) = A.
Le principe d’« exploration à partir du meilleur » consiste à chercher, parmi les sommets visités non encore calculés, un sommet dont la valeur m(x) est minimum. On peut alors démontrer que, pour un tel sommet, les valeurs « provisoires » m(x), p(x) sont définitives (et correctes). Cette démonstration utilise explicitement le fait que les valeurs sont non négatives.
On marque donc x comme calculé et on « prolonge » l’exploration en examinant chacun des successeurs de x : chaque successeur y non encore visité devient visité, avec m(y) = m(x) + v(y, x), p(y) = x tandis que, pour chaque successeur y déjà visité, on effectue la mise à jour m(y) = min(m(y), m(x) + v(x, y)) (et p(y) = p(x) si m(y) est mis à jour). L’exploration s’arrête lorsque tous les sommets visités sont calculés (les sommets non visités sont inaccessibles, on peut considérer qu’ils ont une valeur m(x) = ∞).
L’algorithme peut s’écrire de cette façon :
/* Initialisations */
calculés = {A} ;
m(A) = 0 ;
provisoires = ∅ ;
pour tout sommet y successeur de A
provisoires = provisoires ∪ {y} ;
m(y) = v(A,y) ;
p(y) = A ;
fpour
/* Itérations */
tant que provisoires ≠ ∅
soit x ∈ provisoires tel que m(x) est minimum sur provisoires ;
calculés = calculés ∪ {x} ;
provisoires = provisoires - {x} ;
pour tout sommet y successeur de x
cas
y ∈ calculés : rien
y ∈ provisoires :
si m(x) + v(x,y) < m(y)
m(y) = m(x) v(x,y) ;
p(y) = x ;
fsi
autrement :
provisoires = provisoires ∪ {y} ;
m(y) = m(x) + v(x,y) ;
p(y) = x ;
fcas
fpour
ftantque
/* les sommets n'appartenant pas à calculés sont inaccessibles */
La complexité de l’algorithme est de l’ordre de n2, mais cette complexité peut être facilement réduite à n + m, où m désigne le nombre d’arcs du graphe, grâce à une structure de données sophistiquée.
S’il y a n sommets, l’algorithme nécessite au plus n – 1 étapes. À l’étape k, il faut calculer un minimum sur l’ensemble provisoires (de cardinal au plus égal à n – k), puis, pour le sommet choisi x, examiner ses successeurs non calculés (leur nombre est au plus égal au nombre d’arcs issus de x). Globalement, il y a donc au plus n2 + m opérations, où m est le nombre d’arcs du graphe (somme du nombre d’arcs issus de chacun des sommets). Comme m ≤ n2, le nombre d’opérations est, au pire, proportionnel au carré du nombre de sommets.
3. Le magnifique algorithme général de Roy-Warshall-Floyd
Cet algorithme est dû à R. Floyd, qui l’a publié en 1962 (« Algorithm 97 : Shortest Path », Comm. of the ACM, 5, 1962, p. 345). Il s’agit en fait d’une généralisation au cas des graphes valués d’un algorithme de calcul de fermeture transitive d’un graphe, trouvé à peu près simultanément en France par B. Roy (« Transitivité et connexité », CRAS 249, 1959, pp. 216-218) et aux États-Unis par S.Warshall (« A Theorem on Boolean Matrices », Journal of the ACM, 9(1), 1962, pp. 11-12). Il est bien difficile de savoir si chacun d’eux était au courant des travaux de l’autre, mais, malheureusement, la contribution originale de B. Roy est souvent oubliée dans les références. Nous souhaitons donc contribuer à réparer cette injustice.
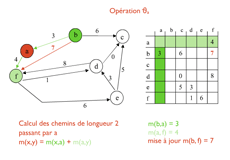
Un exemple de déroulement de l’algorithme de Roy-Warshall-Floyd.
Principe de l’algorithme
Il s’agit ici de calculer, pour tout sommet x et tout sommet y, la valeur minimale des chemins de x à y, notée m(x,y). C’est un algorithme applicable dans tous les cas, et dont la complexité est de l’ordre de n3. De plus, cet algorithme peut gérer le routage, déterminer l’ordre dans lequel les sommets sont visités.
Cette animation Flash présente un exemple de déroulement de l’algorithme de Roy-Warshall-Floyd. Pour la visionner, Adobe Flash Player est nécessaire.
Supposons que les sommets soient numérotés 1,2, …,n (ce qui est toujours possible !). Le graphe est composé de l’ensemble fini de ces sommets, et d’un ensemble de couples de sommets, appelé ensemble des arcs. Chaque arc (x,y) est doté d’une valeur notée v(x,y). Initialement, on a, pour tout couple de sommets (x,y), les valeurs m(x,y)=v(x,y) si l’arc (x,y) existe (cet arc correspond à un chemin de longueur 1, c’est-à-dire allant directement de x à y sans passer par un autre sommet – attention de ne pas confondre longueur et valeur), ou m(x,y)= +∞ si l’arc est inexistant.
Une première opération, nommée ϑ1, va calculer, pour chacun des couples de sommets (x,y), la valeur minimum des chemins de x à y entre celui de longueur 1 (l’arc (x,y)) et celui de longueur 2, sans répétition, passant par le sommet numéro 1, c’est-à-dire le chemin (x,1,y). Cette opération est très simple : elle consiste à calculer, pour tout x et tout y, la valeur m(x,y)=min(m(x,y),m(x,1) + m(1,y)).
Puis une deuxième opération, nommée ϑ2, va calculer, pour chacun des couples de sommets (x,y), la valeur minimum des chemins de x à y parmi celui de longueur 1 (l’arc (x,y)), ceux de longueur 2, sans répétition, passant par les sommets numéro 1 ou 2, c’est-à-dire (x,1,y) et (x,2,y), et ceux de longueur 3, sans répétition, passant par les sommets 1 et 2, c’est-à-dire les chemins (x,1,2,y) et (x,2,1,y). Elle consiste à calculer, pour tout x et tout y, la valeur m(x,y)=min(m(x,y),m(x,2) + m(2,y)) où les valeurs m( , ) sont celles mises à jour par ϑ1.
Et ainsi de suite, avec les opérations ϑ3, …, ϑk, …,ϑn.
On peut voir que, à l’issue de ϑk (1≤k≤n) chaque valeur m(x,y) est la valeur minimum des chemins de x à y, sans répétition, passant par les sommets intermédiaires de numéro ≤k (ces chemins sont donc de longueur ≤k + 1).
Par conséquent, à l’issue de ϑn, les valeurs m(x,y) prennent en compte l’ensemble de tous les chemins sans répétition allant de x à y (tous les sommets intermédiaires possibles sont pris en compte).
S’il n’y a pas de circuit absorbant, ces valeurs sont correctes. S’il y a des circuits absorbants (de valeur <0), ils sont détectés, puisque pour chaque sommet x appartenant à un tel circuit, on a m(x,x)<0.
L’algorithme peut s’écrire de la façon suivante :
/* initialisation */
pour x depuis 1 jqa n
pour y depuis 1 jqa n
si y est successeur de x
m(x,y)=v(x,y) ;
sinon m(x,y)= + ∞;
fsi
fpour
fpour
/* opérations ϑ */
pour k depuis 1 jqa n
/* opération ϑk*/
pour x depuis 1 jqa n
v=m(x,k) ;
pour y depuis 1 jqa n
w=v + m(k,y) ;
si w<m(x,y)
m(x,y)=w ;
fsi
fpour
fpour
fpour
si existe x tel que m(x,x)<0 "il y a des circuits absorbants" fsi
Et le tracé des chemins ?
Pour connaître l’ordre dans lequel les sommets sont visités, chaque sommet x est muni d’une table de routage R(x), qui associe à chaque sommet y la valeur R(x)[y]=successeur de x sur le meilleur chemin menant vers y (ou 0 s’il n’y a pas de chemin de x vers y).
Ces tables sont mises à jour par les opérations ϑ, et restent cohérentes avec les valeurs successives des m(x,y). Initialement, R[x](y) vaut y si y est successeur de x, et vaut 0 sinon (car seuls les arcs, ou chemins de longueur 1, ont été pris en compte à ce stade). Considérons ensuite une opération ϑk (avec 1≤k≤n). Si m(x,y) est modifié par cette opération, cela veut dire que le meilleur chemin de x à y devient un chemin passant par le sommet numéro k. Donc, pour aller de x vers y en suivant ce chemin, il faut se diriger vers le sommet k, et donc suivre le meilleur chemin de x à k. Ceci est indiqué en attribuant R(x)[y]=R(x)[k]. Il suffit d’ajouter ces mises à jour dans le texte de l’algorithme, comme montré ci-après :
/* initialisation */
pour x depuis 1 jqa n
pour y depuis 1 jqa n
si y est successeur de x
m(x,y)=v(x,y) ;
R(x)[y]=y ;
sinon m(x,y)= +∞; R[x](y)=0 ;
fsi
fpour
fpour
/* opérations ϑ */
pour k depuis 1 jqa n
/* opération ϑk */
pour x depuis 1 jqa n
v=m(x,k) ;
pour y depuis 1 jqa n
w=v + m(k,y) ;
si w<m(x,y)
m(x,y)=w ;
R(x)[y]=k ;
fsi
fpour
fpour
fpour
si existe x tel que m(x,x)<0 "il y a des circuits absorbants" fsi
L’algorithme comporte trois boucles imbriquées, chacune exécutant n pas. Il y a donc de l’ordre de n3 opérations élémentaires. Il a été prouvé que, sur un graphe quelconque, cette complexité est optimale.
Le texte de l’algorithme montre une possible amélioration : dans l’opération ϑk, si on constate que v(x,k)= +∞, alors il est inutile de lancer la boucle sur y, puisque, quel que soit y, v(x,k) + v(k,y)= +∞ qui ne peut pas être inférieur à v(x,y). D’autres améliorations seraient possibles, par exemple, si l’on sait qu’un sommet y est sans successeur, l’opération ϑy ne provoquera elle non plus aucune mise à jour, on peut donc l’omettre.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !
