
Le problème des 8 reines… et au-delà
Une première version de cet article est parue dans la revue Pour la Science, n°459, en janvier 2016.
En 1848, un joueur d’échecs allemand, Max Bezzel, pose le problème suivant : est-il possible de placer 8 reines sur l’échiquier de façon qu’aucune ne soit « en prise » (sous le feu d’une autre) ? Rappelons qu’une reine menace toutes les cases de la ligne, de la colonne et des deux diagonales passant par la case qu’elle occupe. Puisqu’il n’y a que 8 lignes horizontales sur l’échiquier, et qu’une reine au plus peut se trouver sur une telle ligne dans une solution du problème, il est certain qu’il n’y aura pas plus de 8 reines indépendantes sur l’échiquier 8 × 8 : s’il existe des solutions, elles comporteront toutes une reine par ligne au maximum. Il en va de même pour les colonnes et les diagonales.
Carl Friedrich Gauss (1777-1855) étudia le problème et le résolut partiellement en proposant 72 solutions avec, pour chacune, 8 reines sur l’échiquier de 64 cases, mais il avait oublié certaines solutions. La première solution complète fut proposée en 1850, par Franz Nauck. Il existe 92 dispositions convenables, donc 20 de plus que celles trouvées par Gauss. Elles se réduisent à 12 quand on enlève les configurations se déduisant d’une autre par des rotations ou des symétries. Deux de ces 12 solutions ont une jolie propriété : il n’existe jamais trois dames alignées, quelles que soient les droites envisagées. Essayez de les trouver (sans consulter l’encadré ci-dessous).
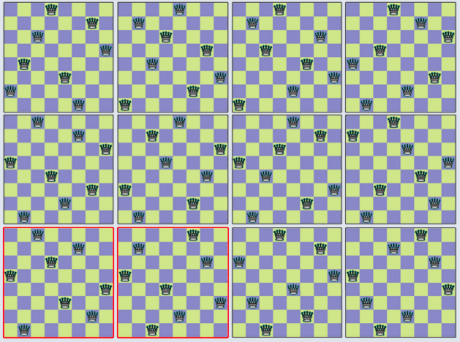
On cherche à placer le plus grand nombre possible de reines sur l’échiquier de 64 cases, sans qu’aucune de ces reines ne soit en prise sur une autre.
On ne peut en placer que 8 au plus, car il est impossible d’en mettre 2 sur la même ligne (ou la même colonne). On découvre par tâtonnements qu’il existe des configurations satisfaisantes avec 8 reines.
Il y en a 92, qui se réduisent à 12 quand on retire les configurations identiques à une symétrie près ou à une rotation près. Parmi ces solutions, 2 ont la propriété de ne contenir aucun triplet de reines alignées, ce sont les solutions dont le cadre est ici marqué en rouge.
La généralisation du problème de Bezzel consiste à envisager un échiquier carré de n cases de côté et à essayer d’y placer n reines. C’est le « problème des n reines ». On découvre sans mal que pour n = 2 et n = 3, c’est impossible. En revanche, pour n ≥ 4, cela semble toujours possible. On envisage deux aspects du problème :
(i) trouver pour tout n une solution, s’il en existe ;
(ii) trouver toutes les solutions ou seulement les dénombrer, au moins pour les premières valeurs de n.
Une solution, oui ; toutes les solutions, non
Le problème (i) est aujourd’hui parfaitement résolu, cela sans avoir besoin d’un ordinateur : on décrit un procédé général sous forme géométrique qui, pour tout n ≥ 4, construit une configuration convenable. De tels procédés sont nombreux et on en découvre régulièrement de nouveaux.
La version (ii) est bien plus délicate. Imaginer des procédés simples qui, pour tout entier n, décrivent toutes les solutions ne semble pas envisageable. On utilise donc des ordinateurs pour effectuer des calculs systématiques. C’est un exercice de programmation que tout étudiant en informatique a pratiqué au moins une fois. Il est assez facile d’écrire un programme qui traite le problème jusqu’à n = 12. Aller au-delà demande plus de soin et de patience et fait l’objet de records qui, à cause de l’explosion combinatoire, évoluent lentement. À ce jour, le décompte des solutions a été mené jusqu’à n = 26. Réussir ce décompte pour n = 27 apparaît un défi difficile : on en est à n = 26 depuis plus de cinq ans.
À défaut de connaître le nombre exact de solutions pour tout n, on essaie de minorer ce nombre, car il est intéressant de savoir (et de démontrer) que le nombre de solutions augmente très rapidement avec n. Quelques minorations sont connues et les raisonnements qui y mènent sont assez intéressants. Nous allons en présenter un et expliquer comment plusieurs mathématiciens ont été piégés et ont proposé de faux raisonnements repris parfois sans vérification dans la littérature sur le sujet. Auparavant, présentons la méthode pour obtenir au moins une bonne configuration pour chaque entier n ≥ 4.
Pour trouver une solution pour n quelconque, l’idée la plus simple, proposée dès 1874 par Emil Pauls, est de disposer les reines régulièrement selon un double parcours rectiligne de cavalier, en s’arrangeant pour qu’il y ait une reine sur chaque ligne et une sur chaque colonne.
La méthode est parfaite (voir échiquiers 1 et 2 de l’encart ci-dessous) pour tout entier n multiple de 6 (c’est-à-dire n = 6m où m est un entier), et pour tout n supérieur de 4 unités à un multiple de 6 (c’est-à-dire n= 6m + 4). Pour les nombres pairs supérieurs de 2 unités à un multiple de 6 (soit n = 6m + 2), la méthode ne convient pas à cause des diagonales (voir échiquier 3). Un autre schéma un peu plus compliqué permet de s’en tirer (voir échiquiers 4 et 5). On a donc une solution pour tout entier pair supérieur ou égal à 4.
Pour les nombres impairs, soit n = 2m + 1, on prend une solution pour le nombre pair inférieur d’une unité, soit 2m, on la place dans le coin en bas à gauche de l’échiquier de côté 2m + 1, et l’on ajoute une reine dans le coin en haut à droite (voir échiquiers 6 et7). Le problème (i) de trouver une solution pour tout entier n ≥ 4 est donc résolu… sans avoir utilisé d’ordinateur. Disposer d’une solution, c’est très bien, mais les connaître toutes ou réussir à les compter, ce serait encore mieux. À moins d’une découverte mathématique, l’ordinateur semble cette fois indispensable.
Pour montrer que le problème des n reines a au moins une solution pour tout entier n ≥ 4, il n’y a pas besoin d’ordinateur : il suffit de réfléchir. En plaçant des reines selon deux lignes obliques, on obtient un schéma qui marche parfaitement pour les nombres pairs n de la forme 6m + 4 (échiquier 1, n = 10), où m est un entier positif ou nul, et de la forme 6m (échiquier 2, n = 12), mais pas quand n est de la forme 6m + 2 (échiquier 3, n = 8).

Il faut traiter à part le cas où n est de la forme 6m + 2. C’est assez facile : on part de deux lignes obliques de reines (échiquier 4), puis on déplace 4 reines (échiquier 5).

Lorsque n est impair, la solution se déduit des solutions trouvées pour le cas où n est pair : on reprend les solutions pour les cas pairs en ajoutant une reine en haut à droite sur l’échiquier agrandi d’une ligne et d’une colonne (échiquiers 6 et 7).

Des ruses pour chercher toutes les solutions
Nous allons envisager trois façons de plus en plus « intelligentes » de rechercher toutes les solutions pour une valeur donnée de n. Cette progression de la puissance quand on améliore les méthodes illustre l’idée qu’en informatique, un programme peut être juste et fonctionner parfaitement pour les petites valeurs d’un paramètre, et pourtant être inefficace car conduisant à des temps de calcul irréalistes (des années, des siècles ou plus !) quand le paramètre augmente.
On commence par écrire un sous-programme qui, quand on lui donne une configuration quelconque de n reines, indique si oui ou non elle est satisfaisante. Un tel sous-programme est facile à concevoir, car deux dames en positions (a, b) et (a’, b’) sur l’échiquier de côté n (où a, a’, b, b’ varient de 1 à n) sont en prise l’une avec l’autre si et seulement si a = a’ (elles sont sur la même ligne) ou b = b’ (même colonne) ou a – b = a’ – b’ (même première diagonale) ou a + b = a’ + b’ (même seconde diagonale).
La première idée pour calculer toutes les solutions pour n donné consiste à placer n reines de toutes les façons possibles et pour chaque configuration, d’utiliser le sous-programme qui indiquera si la configuration est solution ou non. Il y a n2 choix possibles pour la première reine, n2 choix pour la deuxième, etc., jusqu’à la n-ième. Le nombre de configurations à tester est donc exactement (n2)n = n2n, ce qui, pour n = 8, fait environ 2,815 × 1014.
La deuxième idée consiste à remarquer que toute solution s’obtiendra en plaçant une reine par colonne, et qu’on peut même s’arranger pour que les reines placées ne soient pas sur les lignes déjà occupées au moment où on les place. Il y a ainsi n façons de placer la première reine dans la première colonne, n – 1 façons de placer la deuxième reine sur la deuxième colonne, n – 2 façons de placer la troisième reine sur la troisième colonne, etc.
Cela conduit donc à tester en tout n ! configurations de n reines. On les teste une à une avec le sous-programme décrit plus haut, qui peut d’ailleurs être simplifié puisque, par construction, les configurations qu’on lui soumet maintenant sont correctes pour les contraintes de lignes et de colonnes. Le gain entre la première méthode et la seconde est considérable. Pour n = 8, il n’y a plus que 40 320 configurations à tester, soit environ 7 milliards de fois moins qu’avec la première méthode !
On peut encore faire mieux. La troisième méthode consiste à remarquer que lorsqu’on place les reines une à une comme dans la deuxième méthode, on peut s’apercevoir rapidement qu’on est en train de construire une configuration qui échouera. Si par exemple on a placé une reine en (1, 1), puis la seconde en (2, 2), elles sont sur la même diagonale : il faut donc cesser de construire cette configuration qui ne donnera jamais de solution, quelles que soient les reines qu’on y ajoutera. Découvrir le plus tôt possible deux reines en prise dans l’énumération ordonnée de toutes les possibilités et remettre en cause le choix qui y a conduit est ce qu’on nomme la méthode de backtracking, ou retour arrière. Elle est d’usage courant dans de nombreux problèmes combinatoires.
Le gain obtenu par rapport à la seconde méthode est encore très intéressant et augmente avec n. Si l’on compte comme un essai une position où soit on a réussi à trouver une solution, soit on a découvert qu’il sera impossible d’aller plus loin, alors on trouve les 92 solutions pour n = 8 en 13 756 essais. Cela correspond à trois fois moins d’essais qu’avec la deuxième méthode. Pour n = 12, on n’effectue que 9 261 880 essais au lieu de 12 ! = 479 001 600 avec la deuxième méthode ; on a donc gagné un facteur 50. Notons que la seule façon de connaître le nombre d’essais par la troisième méthode est de l’appliquer complètement, car on ne connaît aucune formule simple donnant ce nombre.
Le record : 26 reines
Il se trouve cependant que pour battre les records, il faut non seulement utiliser une bonne méthode, donc une variante du backtracking, mais aussi :
– la programmer très soigneusement ;
– faire exécuter en parallèle les calculs (ce qui n’est pas difficile ici car la méthode s’y prête bien) ;
– fabriquer et utiliser des puces spécialisées qui iront plus vite que les processeurs généraux pour l’exécution des calculs.
C’est ainsi que fonctionne le système informatique aujourd’hui détenteur du record pour n = 26. Ce record est détenu par l’université technique de Dresde (projet Queens@TUD), en Allemagne. Les chercheurs ont conçu une méthode massivement parallèle utilisant des circuits FPGA (field programmable gate array) adaptés à ce calcul. Ce dernier a tout de même duré dix mois et s’est terminé le 11 juillet 2009. Il a abouti à 22 317 699 616 364 044 (22 millions de milliards) solutions au problème des 26 reines. Depuis, le résultat a été confirmé par un calcul effectué par des Russes, mais le dénombrement des solutions n’a pas été effectué pour 27 reines ou plus.
Notons que si l’on cherche non pas une ou toutes les solutions, mais seulement quelques solutions, par exemple une centaine, alors d’autres méthodes de programmation sont envisageables. L’une d’elles consiste à placer au hasard une reine par colonne, ce qui donne une configuration très probablement incorrecte. On corrige ensuite celle-ci en déplaçant les reines une à une, de telle sorte qu’à chaque déplacement, le nombre de conflits (c’est-à-dire de couples de reines en prise) diminue. On sait, par ce type d’algorithmes, trouver rapidement des solutions pour n = 100 ou même n = 1 000. Un algorithme quantique a aussi été présenté qui permettra peut-être de battre le record de n = 26… le jour où l’on disposera d’ordinateurs quantiques de taille respectable, ce qui n’est pas le cas aujourd’hui.
Ceux que la programmation du problème intéresse trouveront une multitude de programmes traitant des n reines, écrits dans une grande variété de langages de programmation, sur le site internet N-queens problem. À défaut de calculer le nombre exact de solutions pour tout n, on aimerait prouver que ce nombre augmente rapidement avec n (cela semble évident au vu des résultats connus de décompte jusqu’à n = 26). Nous décrirons une telle méthode, mais nous envisagerons d’abord une variante du problème des n reines introduite par le mathématicien d’origine hongroise George Pólya (1887-1985).
Pólya imagine un échiquier n × n dessiné sur un tore (la surface d’une chambre à air) (voir la figure A ci-dessous) et cherche des solutions au problème des n reines sur cet échiquier torique.

A. Partant d’un échiquier de côté n en caoutchouc, on colle le bord droit avec le bord
gauche (en rouge). On obtient un échiquier cylindrique. On colle alors les deux extrémités du cylindre (bords verts), ce qui donne un tore. Les diagonales du carré initial se sont rejointes et il y en a maintenant n dans chaque sens, chacune ayant n cases.
Les contraintes sur les lignes et les colonnes ne changent pas. En revanche, pour les diagonales, cela se complique, car les diagonales se rejoignent désormais, comme si le bord droit était collé au bord gauche et le bord du haut au bord du bas (selon un principe souvent utilisé dans les jeux vidéo). Par conséquent, une configuration résolvant le problème des n reines sur l’échiquier normal n’est plus nécessairement une solution sur l’échiquier torique (voir les échiquiers B et C ci-dessous).
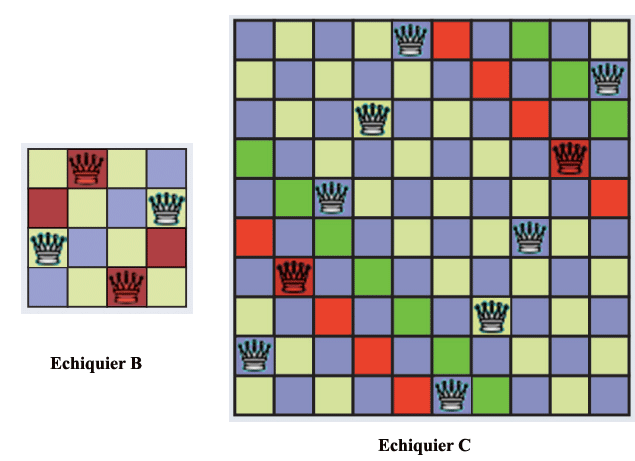
B. La diagonale rouge de cet échiquier torique contient deux reines. Cette solution au problème plan des 4 reines n’est donc pas une solution pour le problème torique.
C. Cette solution au problème plan des 12 reines n’en est pas une pour le problème torique : la diagonale rouge contient deux reines (ici, la diagonale verte n’en contient aucune).
Des reines sur un échiquier torique
Pólya a établi qu’il ne pouvait exister de solutions à ce problème que si n est de la forme 6m + 1 ou 6m – 1 pour un certain entier m. Le nombre de solutions est donné par une suite T(n) dont les premiers termes non nuls sont : T(5) = 10, T(7) = 28, T(11) = 88, T(13) = 4 524, T(17) = 140 692.
Propriété intéressante : si l’on dispose d’une solution torique et qu’on en pave tout le plan en utilisant le pavage habituel du plan par un carré, on obtient un dessin dont tout carré extrait de taille n × n est encore une solution torique du problème des n reines (voir l’échiquier D ci-dessous).

D. Pour n = 5, le problème torique a 10 solutions (l’une d’elles est représentée, avec un cadre marron). Une solution du problème torique des n reines permet d’en obtenir beaucoup d’autres : en pavant le plan par des carrés solutions du problème torique des n reines et en extrayant un carré n × n n’importe où dans le plan ainsi pavé, on obtient une autre solution du problème torique (cadres rouges).
L’intérêt des solutions toriques est surtout qu’on peut les exploiter pour construire automatiquement une multitude de grandes solutions à partir de quelques petites. La méthode est visuelle : on prend une solution du problème plan des n reines (par problème plan, nous entendons le problème habituel) et l’on remplace dans cette solution chaque reine par une solution du problème torique des m reines. Cela donne une configuration de reines sur l’échiquier de côté n × m qui est une solution au problème plan des n × m reines (les menaces qui auraient pu se produire en diagonale entre les différentes copies de la solution torique sont évitées par les diagonales allongées de l’échiquier torique).

E. La « composition » d’une solution plane des 4 reines avec une solution torique des 5 reines fournit une solution au problème plan des 20 reines. En « composant » ainsi les solutions du problème torique des n reines avec des solutions du problème plan des m reines, on obtient un grand nombre de solutions au problème plan des n × m reines.
Le nombre de solutions croît exponentiellement
La méthode de composition permet d’établir que le nombre de solutions au problème des n reines augmente exponentiellement avec n, ce que l’on a constaté jusqu’à n = 26, mais qu’il est bon de démontrer rigoureusement pour n tendant vers l’infini.
Voici un exemple de raisonnement. Puisqu’il y a 10 solutions au problème torique des 5 reines, en les combinant de toutes les façons possibles, l’une quelconque des 10 avec l’une quelconque des 10, on obtient 100 solutions au problème des 25 reines. Il est facile de s’assurer qu’elles sont différentes. En recommençant à partir de ces 100 solutions au problème des 25 reines, on obtient 1 000 solutions au problème des 125 reines, puis 10 000 solutions au problème des 625 reines, et, plus généralement, 10m solutions au problème des 5m reines. Pour les entiers n de la forme 5m, on a donc 2n fois plus de solutions que de nombre de reines. En partant de T(7) = 28, on aurait obtenu 28n solutions au problème des 7n reines, soit 4n fois plus de solutions que de reines.
On a bien une démonstration que le nombre de solutions augmente très vite lorsque le nombre de reines est une puissance de 5. En fait, le nombre de solutions comparé au nombre de reines semble croître bien plus vite encore que ne l’indique notre démonstration.
Notons, avant d’en venir aux conjectures, que la méthode décrite permet de concevoir une solution sur l’échiquier infini : du problème torique des 5 reines, on prend la solution présentant une reine au centre et on la combine indéfiniment avec elle-même, ce qui conduit à une solution (ayant une reine sur chaque horizontale, chaque verticale et même chaque diagonale) du plan infini (voir l’encart ci-après).
La méthode de composition des solutions donne aussi la démonstration qu’il existe des solutions au « problème infini des reines ». Ce problème consiste à placer des reines sur un échiquier infini de sorte qu’il y en ait une par ligne, une par colonne, une par diagonale parallèle à la droite y = x, et une par diagonale parallèle à la droite y = –x.
On procède progressivement : du problème torique des 5 reines, on prend la solution ayant une reine en son centre. On remplace chaque reine par la configuration elle-même (et l’on subdivise les autres cases). Cela donne une configuration convenable sur l’échiquier 25 × 25. De plus, cette configuration prolonge la première, en ce sens qu’on peut la voir comme l’addition de 20 nouvelles reines aux 5 reines initiales. On répète la même opération, ce qui prolonge la solution qu’on a sur un échiquier 25 × 25 en une solution sur l’échiquier 125 × 125, puis sur un échiquier 625 × 625, etc. À chaque fois, les nouvelles configurations sont compatibles avec les précédentes, ce qui autorise à « passer à l’infini », c’est-à-dire à considérer simultanément toutes les reines qui sont déposées d’étape en étape. On a la solution recherchée.
La méthode donne ici une seule solution au problème infini des reines, mais on l’adapte pour montrer qu’il existe une infinité de solutions différentes à ce problème, que cette infinité de solutions n’est pas dénombrable et qu’elle est de même cardinal que le continu : il y a autant de solutions au problème infini des reines que de points sur une droite !

La conjecture qui semble la plus probable est que si l’on note R(n) le nombre de solutions au problème des n reines, alors log R(n)/(n log n) tend, quand n tend vers l’infini, vers une constante qui vaut à peu près 0,44438… Si c’est vrai, cela signifie que R(n) augmente aussi vite que n0,44438n : c’est beaucoup plus rapide que ce que nous avons su démontrer avec la méthode des solutions toriques de Pólya.
Signalons que certains mathématiciens se sont fait piéger en utilisant la méthode de composition. Ils ont pensé que l’on pouvait remplacer les reines de la solution plane par des solutions différentes du problème torique, ce qui est faux. La démonstration des minorations obtenues est donc fausse, bien que ces minorations soient reproduites dans divers articles, dont celui de Jordan Bell et Brett Stevens de 2009, très souvent cité (voir la bibliographie), où le Theorem 2 n’est en réalité qu’une conjecture.
D’autres jeux
Les échecs sont un jeu de raisonnement et intéressent donc de nombreux mathématiciens. Cependant, les problèmes d’échecs semblent un peu trop liés aux règles précises du jeu lui-même. Aussi les mathématiciens se sont-ils amusés à concevoir des énigmes combinatoires plus pures, tels le problème des n reines ou le tout aussi populaire problème du parcours du cavalier (faire circuler un cavalier de telle façon qu’il passe par chaque case de l’échiquier une fois exactement) qui a passionné Euler. Ce ne sont pas les seules. Les livres de John Watkins ou l’énorme mémoire gratuit (en anglais et en tchèque !) de Václav Kotěšovec en mentionnent un grand nombre (voir la bibliographie). Ces problèmes ont stimulé le développement de la théorie des graphes et resteront longtemps une source précieuse de défis informatiques et mathématiques.
- S. Kapplusch, Raising the bar – New world record by exploring the 27-queens puzzle on FPGAs, 2016 (consulté le 18 novembre 2020).
- Rosetta Code, N-queens problem, 2015 (consulté le 18 novembre 2020).
- V. Kotěšovec, Non-attacking chess pieces, 2013 (PDF téléchargeable sur son site, consulté le 18 novembre 2020).
- T. B. Preußer et J. Ward, 27-Queens Puzzle: Massively Parellel Enumeration and Solution Counting, 2016 (consulté le 18 novembre 2020).
- J. Bell et B. Stevens, A survey of known results and research areas for n-queens, Discrete Mathematics, vol. 309(1), pp. 1-31, 2009 (attention, Theorem 2 n’est en fait qu’une conjecture).
- J. J. Watkins, Across the Board : The Mathematics of Chessboard Problems, Princeton University Press, 2007.
- I. Rivin et al., The n-queens problem, Amer. Math. Monthly, vol. 101(7), pp. 629-639, 1994 (attention, le théorème 2 et son corollaire sont faux).
- P. Campbell, Gauss and the eight queens problem : A study in miniature of the propagation of historical error, Historia Mathematica, vol. 4(4), pp. 397-404, 1977.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).