Le son des timbales
Dans son Journal, l’écrivain et diplomate Paul Claudel notait : « La musique est l’âme de la géométrie. » Plus prosaïquement, quand un mélomane voit un orchestre, il suit l’entrée en action des différents musiciens et, d’une certaine façon, « visualise » la partition à mesure qu’elle est jouée. Les phénomènes acoustiques qui se propagent dans l’air entre les musiciens et les spectateurs restent, quant à eux, invisibles. Pourtant, si l’on voyait les ondes sonores, on aurait directement accès aux mécanismes physiques à la base des sensations musicales. La « force sonore », par exemple, ou l’intensité subjective qui nous fait percevoir un son plus ou moins fort, dépend de l’amplitude des fluctuations de pression qui arrivent à nos tympans tandis que la « hauteur » d’une note, son caractère plus ou moins aigu, dépend de la fréquence des vibrations acoustiques. Le « timbre », qui distingue la guitare du violon, ou encore les cuivres des bois, est quant à lui le résultat d’une riche alchimie mêlant, notamment, la taille d’un instrument, sa forme et les propriétés élastiques des matériaux qui le constituent.
Trois sensations déterminent la façon dont nous percevons les sons : l’intensité, la hauteur et le timbre. L’intensité subjective, ou force sonore, est la sensation qui fait paraître un son fort ou faible. Elle croît avec l’amplitude des ondes de pression acoustiques qui atteignent le tympan de l’oreille.
Selon sa hauteur, un son est aigu ou grave. La hauteur d’un son dépend de sa période : plus la période est courte, plus le son paraît aigu. Cependant, la plupart des sons ne sont pas périodiques et il est parfois difficile de leur attribuer une hauteur. Lorsque le son est périodique ou quasi périodique, comme celui d’une flûte ou d’un piano, l’énergie de l’onde sonore se répartit sur plusieurs fréquences bien distinctes. La distance entre ces fréquences est un multiple entier d’une fréquence dite fondamentale (cette fréquence fondamentale n’est autre que l’inverse de la quasi-période du son). La plupart des instruments de percussion produisent des sons non périodiques. Dans ce cas, l’énergie sonore est répartie sur des fréquences dont les valeurs n’ont pas de relations entières ou fractionnaires entre elles. On dit que l’on a un spectre « inharmonique ». Ce type de spectre n’engendre pas de sensation de hauteur bien nette. Il peut même, comme c’est le cas pour certaines cloches, évoquer plusieurs hauteurs simultanément. Les bruits du vent ou de la mer, quant à eux, présentent des spectres continus et l’on n’y perçoit aucune hauteur.
Le timbre, enfin, dépend beaucoup de la méthode employée pour faire vibrer l’instrument. Ainsi, par exemple, on classe les instruments à cordes en fonction du mécanisme de mise en vibration : cordes pincées (guitare), frappées (piano) ou frottées (violon). Plusieurs expériences ont montré que si, dans un enregistrement, on efface le début du son (« l’attaque » de la corde), c’est-à-dire le moment où l’interaction avec l’outil utilisé pour exciter les cordes est prépondérante, on reconnaît très difficilement l’instrument.
Par ailleurs, les instruments à cordes et les percussions ont ce que l’on nomme une signature spectrale caractéristique. Celle-ci dépend de leur géométrie, de leur taille et des matériaux utilisés. Ces propriétés déterminent en effet des modes de vibration propres à l’instrument, qui sont sélectionnés et privilégiés dans l’ensemble des fréquences engendrées lors de la production d’un son. En se basant uniquement sur des critères physiques d’adaptation entre tessiture et dimensions, on aboutit alors à une géométrie « optimale » en termes de taille d’instruments. Ainsi, on cherche à favoriser plus volontiers la tessiture moyenne et grave d’un violoncelle ou d’une contrebasse, tandis que l’on favorise plutôt la tessiture aiguë pour le violon. En règle générale, plus les instruments sont petits, plus les sons produits sont aigus. Il est facile de s’en convaincre en observant les cordes d’un piano, les lames d’un xylophone ou la taille des tambours d’une batterie… Il existe malgré tout des instruments « paradoxaux » qui n’obéissent pas à cette règle. Plusieurs chercheurs, notamment la luthière et acousticienne américaine Carleen Hutchins, ont ainsi montré que certains instruments du quatuor traditionnel présentent une meilleure adaptation que d’autres entre vibrations de cordes et dimensions de la table d’harmonie et de la cavité. Prenons par exemple le cas de l’alto : comparé au violon, cet instrument est bien plus petit que sa tessiture ne le suggère et il présente une mauvaise adaptation. Pourquoi ? Probablement par tradition, mais aussi en raison d’autres critères que ceux relevant purement de l’acoustique, comme la jouabilité. Le problème est que, si l’on veut augmenter les dimensions de l’alto et lui donner des dimensions « optimales » du point de vue de l’adaptation « excitateur-résonateur », il devient difficile à jouer : soit il est trop grand pour être tenu sur le menton, soit il est trop petit pour être posé sur sa base comme un violoncelle…
Le choix des matériaux conditionne la façon dont les sons des instruments à percussion s’atténuent au cours du temps, ce qui, là encore, constitue une dimension essentielle du timbre. Le son d’un triangle, d’un vibraphone ou d’une cloche dure longtemps, car l’amortissement est relativement faible dans le métal. En revanche, le son d’une lame de xylophone en bois ou d’une peau de tambour frappée s’atténue très rapidement.
Chaque famille d’instruments a ainsi son timbre qui la distingue des autres. Une oreille douée pour l’écoute ou exercée par l’apprentissage d’un instrument est également capable de distinguer plusieurs instruments d’une même famille. Un musicien professionnel est même capable de reconnaître de subtiles différences de timbre entre plusieurs notes de même hauteur et de même intensité jouées sur le même instrument.
Faute de rendre visibles les sons produits dans une salle de concert, les nouvelles techniques de simulation numérique nous permettent aujourd’hui de suivre sur un écran d’ordinateur l’évolution de phénomènes acoustiques « virtuels » dont on vérifie qu’ils sont proches des sons réels. En établissant des modèles physiques précis de certains instruments de musique, on simule sur ordinateur les phénomènes vibratoires qui les parcourent et les ondes sonores qu’ils émettent dans l’air environnant. Ces modèles reproduisent précisément le comportement de l’air et de l’instrument au cours du temps. On les utilise pour produire un son réaliste – bien qu’ils ne proviennent pas d’un instrument réel – ou pour visualiser l’évolution des ondes sonores dans l’espace. Les mélomanes peuvent enfin « voir les sons » et étudier les phénomènes physiques qui déterminent leur qualité musicale.

Les mailloches d’un timbalier diffèrent par leur masse, la souplesse de leur manche et la rigidité du feutre qui recouvre leur tête.
Photo : Arghyro Paouri
Nous nous sommes intéressés à un instrument particulier : la timbale (voir aussi Comprendre la guitare acoustique, par A. Chaigne, G. Derveaux et P. Joly). La timbale est formée d’une membrane circulaire : cette « peau » est aujourd’hui fabriquée en mylar, un polymère synthétique. Elle est tendue sur une coque (ou fût) de forme quasi hémisphérique. Pour produire le son recherché, le timbalier frappe sur la peau avec une ou plusieurs « mailloches ». Un petit trou situé dans le fond du fût de la timbale garantit, quand l’instrument est au repos, que les pressions de part et d’autre de la membrane sont égales (sinon, la peau serait trop tendue et vibrerait mal sous la frappe du timbalier).
Vous pouvez apprécier les qualités musicales de la timbale en profitant d’un passage où le timbalier joue seul, sans être couvert par les autres pupitres : focalisez votre attention sur l’ouverture du Trouvère de Verdi, d’Ainsi parlait Zarathoustra de Richard Strauss, sur la symphonie Roulement de timbales de Haydn ou sur les premières mesures du Concerto pour violon de Beethoven. Les timbales ont une fonction rythmique, bien sûr, mais elles ont aussi une couleur musicale. Les timbales engendrent une sensation de hauteur – un coup de timbale est perçu comme plus ou moins aigu – qui, sans être aussi nette que celle d’une flûte ou d’un piano, n’en est pas moins réelle. Lorsqu’on joue de la timbale, cette sensation de hauteur est d’autant plus perceptible que le coup porté sur la peau est proche du bord. À l’inverse, en frappant la membrane au centre, on obtient un son plus sourd. La sensation de hauteur dépend aussi de la rigidité du manche de la mailloche utilisée et de la dureté de son feutre. En concert, le timbalier utilise une série de mailloches de masse et de rigidité différentes. Il choisira une mailloche légère et rigide pour produire un son clair, sec et brillant mais une mailloche lourde et souple pour produire un son plus mat et sourd.
Les systèmes analogues à la timbale sont fréquents, et nombre d’acousticiens du passé, de Hermann Von Helmholtz à Lord Rayleigh, s’y sont intéressés. Le tympan de l’oreille, par exemple, n’est rien d’autre – si l’on excepte la présence des osselets – qu’une membrane tendue devant la cavité de l’oreille moyenne (les timbales sont d’ailleurs nommées timpani, c’est-à-dire tympans, en anglais). La trompe d’Eustache, quant à elle, y joue le même rôle que l’orifice pratiqué dans le fût. Les haut-parleurs et les microphones sont également constitués de membranes tendues sur une cavité non étanche.
L’interaction de trois milieux

Lors d’un coup de timbale, trois milieux interagissent : la membrane, l’air extérieur à l’instrument et l’air enfermé dans le fût.
Infographie : Delphine Bailly
La timbale est un système où interagissent trois milieux : la membrane, l’air enfermé dans le fût et l’air extérieur. Lorsqu’on frappe la peau, il s’établit un « couplage vibro-acoustique » entre ces trois milieux. D’abord, l’impact de la mailloche produit une onde élastique : des « vagues » plus ou moins hautes progressent à la surface de la membrane. Chacun des points de la peau se déplace dans la direction verticale, tandis que les ébranlements progressent horizontalement : l’onde élastique est qualifiée de « transversale ». Cette vibration élastique crée des fluctuations de pression dans l’air, au voisinage de la peau. Par exemple, lorsqu’une région de la peau monte, la pression de l’air repoussé au dessus augmente, et celle de l’air contenu dans le fût diminue. Ces fluctuations de pression s’éloignent de la peau sous la forme d’ondes longitudinales de pression, ou ondes acoustiques, qui progressent dans tout le volume d’air disponible. Les ondes acoustiques engendrées dans la cavité sont réfléchies à la surface du fût et reviennent vers la membrane sur laquelle elles rétroagissent. Les ondes rayonnées vers l’extérieur emportent une partie de l’énergie du système dont les vibrations s’atténuent.
En simulant les phénomènes physiques qui gouvernent l’établissement du son lorsque la mailloche frappe la peau de la timbale, nous sommes en mesure de suivre, au cours du temps, les ondes élastiques engendrées sur la membrane par l’impact et, simultanément, les ondes acoustiques rayonnées respectivement dans l’espace extérieur et dans la cavité. Les résultats de ces calculs peuvent être utilisés pour dessiner, à divers instants, une carte en trois dimensions des variations de pression et des déplacements de la membrane. On obtient ainsi un film de l’évolution du son et des vibrations. À vitesse réelle, ces observations n’offriraient que peu d’intérêt tant les phénomènes sonores sont rapides : dans la réalité, des ondes qui se propagent en moins d’un centième de seconde sont si complexes qu’il faut plusieurs minutes pour en visualiser l’évolution en détail ! En revanche, en ralentissant suffisamment le défilement des images, on peut les étudier avec tout le confort visuel nécessaire. Par ailleurs, une autre façon d’exploiter les résultats des simulations est de les transformer en sons par l’intermédiaire d’un ordinateur muni de haut-parleurs.
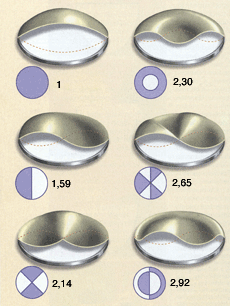
Les six premiers modes de vibration d’une membrane circulaire idéale placée dans le vide ont été représentés avec leur fréquence associée (on a choisi comme unité, la fréquence du premier mode). Pour chacun de ces modes, la membrane oscille entre deux positions : on a représenté une coupe d’une des positions (en beige) et le profil de la position opposée (ligne pointillée rouge). Sur les vues de dessus associées (en violet, par exemple les zones saillantes et en blanc les zones en creux), les secteurs de couleurs différentes se déplacent en sens opposé. Les modes propres sont des ondes stationnaires — elles ne progressent pas sur la membrane — et sont caractérisés par leurs lignes nodales, l’ensemble des points restant immobiles au cours du mouvement (lignes violettes). La peau d’une timbale réelle ne vibre pas exactement selon ces modes propres, et les fréquences qui apparaissent dans le spectre sont légèrement différentes à cause de la présence de l’air et du fût.
Infographie : Delphine Bailly
Si la peau d’une timbale était plongée dans le vide, elle vibrerait comme une membrane circulaire idéale, c’est-à-dire que son mouvement pourrait se décomposer en mouvements élémentaires appelés « modes propres de vibration », qui sont, en quelque sorte, la généralisation à deux dimensions des modes de vibration d’une corde idéale tendue entre deux extrémités fixes. À chaque mode propre correspond une fréquence précise nommée fréquence propre. En première approximation, on pourrait penser que les raies qui apparaissent dans le spectre du son d’une timbale correspondent à ces modes de vibration idéaux. Pourtant, les fréquences des modes de vibration d’une membrane circulaire idéale ne sont pas des multiples d’une fréquence fondamentale (ses vibrations sont inharmoniques), alors que le son des timbales est presque parfaitement harmonique.
Dans la réalité, l’air présent autour de l’instrument interagit avec la peau. L’inertie qu’il oppose au mouvement de la membrane rallonge la période des premiers modes, c’est-à-dire en abaisse les fréquences. Deux autres phénomènes de moindre importance interviennent. Tout d’abord, l’air qui vibre dans la cavité possède aussi ses modes propres (en trois dimensions cette fois), qui peuvent interférer avec ceux de la membrane si leurs fréquences sont proches. Ensuite, la raideur de la peau, c’est-à-dire sa résistance à la déformation, tend à accélérer le retour des points de la surface vibrante vers leur position de repos et, par conséquent, à augmenter légèrement les fréquences des modes les plus rapides. Globalement, ces mécanismes ajustent les fréquences de vibration de la timbale dans des rapports presque harmoniques, par exemple : 1/1,5/2/2,44 (pratiquement 2,5) et 2,90 (pratiquement 3).
Le dédoublement de certaines raies provient des défauts de fabrication de la timbale. La fréquence des différents modes dépend de la force de rappel qui s’exerce sur les points de la membrane lorsqu’ils s’éloignent de leur position d’équilibre. Quand la tension de la peau n’est pas homogène, pour un même mode, des points situés à des endroits différents évoluent à des rythmes légèrement différents. Tout se passe alors comme si l’on avait deux modes au lieu d’un, de fréquences très proches. Or, les musiciens le savent bien, ce type de situation produit habituellement des battements. Un mode de vibration peut donner de l’énergie à son mode jumeau de la même façon que les vibrations engendrées par le pas cadencé des soldats sur un pont peuvent faire entrer l’édifice en résonance si sa fréquence propre est proche de la cadence de la marche. Le mode qui reçoit de l’énergie s’amplifie au détriment de l’autre jusqu’au moment où le flux d’énergie s’inverse. Il s’établit alors un va-et-vient d’énergie entre les deux composantes d’une raie dédoublée. Ce phénomène se traduit par des battements que l’on peut distinguer à l’oreille et, sur le spectre sonore, par des oscillations très nettes de certaines raies au cours de leur décroissance.
Un modèle de timbale
Les simulations numériques élaborées à partir d’un modèle servent à étudier l’effet musical engendré par la modification des paramètres physiques d’un instrument virtuel. Nous pouvons, par exemple, simuler les effets d’une répartition hétérogène de la tension de la peau et en étudier les conséquences musicales, en l’occurrence l’apparition de battements sonores caractéristiques. On peut aussi imaginer la simulation d’instruments que l’on ne saurait fabriquer, une timbale de 20 mètres de diamètre, par exemple ! Ainsi, nous disposons d’un nouvel outil qui permettrait aux compositeurs de mêler des sons produits par des instruments réels et des sons engendrés par des instruments fictifs, mais de la même famille.

La simulation ci-dessus montre le mouvement de la membrane d’une timbale pendant dix millisecondes après l’impact de la mailloche. Les couleurs représentent le déplacement de chaque point par rapport à sa position d’équilibre (de – 0,25 millimètre en bleu à 0,25 millimètre en rouge).
Images : A. Chaigne, P. Joly, L. Rhaouti / Arghyro Paouri
Pour créer notre modèle de timbale, nous introduisons dans l’ordinateur les équations qui rendent compte de l’impact de la mailloche, de la propagation des ondes élastiques sur la membrane, ainsi que de la propagation des ondes acoustiques dans la cavité et dans l’air extérieur. Ces équations sont complétées par des « conditions aux limites », c’est-à-dire par des relations qui imposent le comportement des différentes grandeurs considérées, telles que le déplacement de la membrane et la pression en chaque point de l’air au voisinage de la surface du fût, mais aussi, loin de l’instrument.
En premier lieu, il faut considérer l’action de la mailloche, ce qui revient à étudier comment son énergie cinétique – proportionnelle à sa masse et au carré de sa vitesse – est transférée à la membrane. La masse et la vitesse de la mailloche sont les facteurs déterminants. Toutefois, la rigidité du feutre de la tête de mailloche a également son importance. Quand on comprime entre ses doigts le feutre d’une mailloche, il commence par se déformer facilement, puis il résiste de plus en plus. Cela signifie qu’au début de l’impact, le feutre s’écrase plus qu’il ne déforme la membrane. Il la repousse cependant de plus en plus à mesure que sa résistance à la déformation augmente. Ainsi, l’impulsion imprimée à la peau n’est pas instantanée. La force appliquée au point d’impact évolue au cours du temps, et cette évolution dépend notamment de la rigidité du feutre qui recouvre la tête de la mailloche.
À la suite de cette impulsion, des ondes élastiques transversales se propagent sur la membrane à partir du point d’impact et se réfléchissent sur les bords fixes de l’instrument. Simultanément, la vibration de la membrane crée des fluctuations locales de pression dans l’air situé de part et d’autre. Deux flux d’ondes sonores, deux « champs acoustiques », sont engendrés : l’un rayonne dans l’espace extérieur et l’autre à l’intérieur de la cavité.
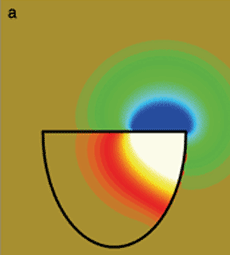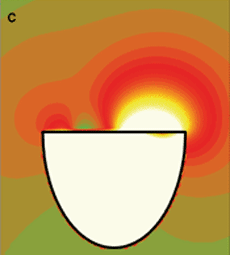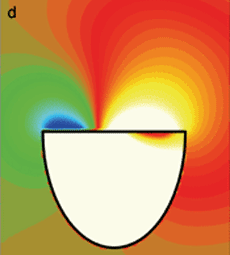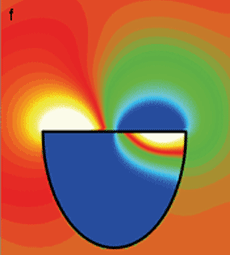
L’évolution de la pression dans l’air environnant a été calculée point par point. Ainsi, on visualise les ondes acoustiques émises à partir de la membrane à l’extérieur et dans l’instrument. La couleur brun-vert dominante sur la première image correspond à la pression ambiante. Les écarts à cette pression vont de -15 pascals (en bleu foncé) à 15 pascals (en jaune pâle). En enfonçant la peau, l’impact de la mailloche crée une dépression locale au-dessus de la membrane et une surpression à l’intérieur du fût (a). Par la suite, ces fluctuations de pression s’éloignent sous la forme d’ondes acoustiques. Cependant, les flux d’ondes acoustiques sont rendus très complexes à cause des interactions entre l’air extérieur, l’air dans le fût et la membrane. Le champ acoustique extérieur se déforme rapidement au cours des dix premières millisecondes (a à f), tandis que celui qui reste dans le fût semble stable pendant plusieurs millisecondes (b à e), puis change brutalement (f).
Images : A. Chaigne, P. Joly, L. Rhaouti
L’évolution de ces ondes de pression est identique dans les deux cas. Elle obéit à des équations de propagation en trois dimensions bien connues des acousticiens. La différence de traitement entre les deux champs acoustiques tient toute entière dans leurs conditions aux limites. Concrètement, dans le cas de l’onde interne à la cavité, on considère que les parois du fût sont parfaitement rigides et que la vitesse des particules d’air s’annule à leur contact (cette condition aux limites en trois dimensions est équivalente à celle imposée aux ondes élastiques qui parcourent la membrane dont les bords sont considérés comme parfaitement fixes).
Dans le cas de l’onde externe, on limite le volume d’espace dans lequel les ondes sont susceptibles de se propager, sinon le calcul durerait indéfiniment… On choisit alors un volume fini englobant l’instrument. Les parois de ce volume sont supposées parfaitement absorbantes pour éviter que les ondes ne s’y réfléchissent et ne reviennent vers l’instrument, ce qui compliquerait inutilement les calculs. Cette hypothèse est réaliste, puisqu’elle correspond assez bien à ce qui se passe dans une chambre dite anéchoïque, où l’on dispose des dièdres absorbants en laine de roche sur les parois afin d’absorber les ondes incidentes.
Il reste maintenant à coupler l’ensemble de ces phénomènes vibratoires (les ondes élastiques dans la membrane) et acoustiques (les ondes de pression dans l’air). Dans le cas présent, on considère que la membrane est légère et souple et que les ondes de pression qu’elle a créées réagissent sur elle et en modifient le mouvement. Quant aux ondes rayonnées vers l’espace extérieur, elles emportent l’énergie du système et contribuent à l’amortissement des vibrations de la membrane. Concernant l’atténuation, il faut tenir compte du fait que les vibrations de la membrane sont amorties dans le matériau de la peau elle-même (l’énergie mécanique des ondes est progressivement transformée en chaleur, à cause de « réarrangements moléculaires » dans le matériau constituant la membrane au cours de la vibration : c’est la viscoélasticité).
Deux heures de calculs pour trois secondes de son
La dernière étape de la modélisation consiste à découper le temps, l’espace et la membrane en petits éléments. Ainsi, à l’aide d’un ordinateur, on calcule l’évolution du système instant par instant, et de proche en proche.
L’espace dans lequel est plongé l’instrument est découpé en cubes élémentaires formant un maillage régulier. Pour que le modèle soit suffisamment fin, il faut que les cubes soient beaucoup plus petits que les longueurs caractéristiques du problème étudié. Dans la pratique, on choisit des cubes dont le côté représente environ un vingtième des longueurs d’onde engendrées au cours de l’expérience simulée (de l’ordre de 2,5 centimètres). Cependant, ce maillage ne tient pas compte de la présence des parois de l’instrument. On y ajoute donc un second maillage, constitué de facettes triangulaires qui représentent le fût et la peau de la timbale et dont on se servira pour calculer les déplacements de la membrane, mais aussi les discontinuités de pression de part et d’autre de l’instrument.
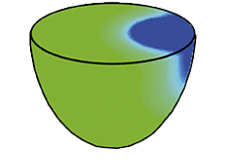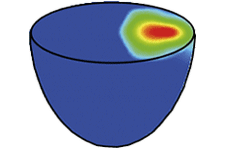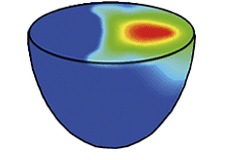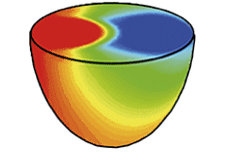
Le saut de pression de part et d’autre de la surface de l’instrument représente les forces agissant sur la membrane et sur le fût, une fois que l’interaction avec la mailloche est terminée. Leur visualisation permet d’identifier la répartition de l’action de l’air qui gouverne le mouvement de la membrane.
Images : A. Chaigne, P. Joly, L. Rhaouti
Au cours de la simulation, le temps s’écoulera par quantités finies toutes égales. Si le pas de temps est trop long, les erreurs s’additionnent rapidement et le paramètre représentant l’énergie « s’accumule » en certains points du domaine simulé : la solution numérique « explose » en un phénomène nommé instabilité numérique. Si, au contraire, le pas de temps est trop petit, les fréquences du système formé par la membrane, l’air extérieur et la cavité ne sont pas bien définies. La durée de ce pas doit donc être, elle aussi, choisie judicieusement. Tout est alors prêt pour lancer les calculs. La pression est calculée explicitement dans chaque élément de volume, à l’aide des valeurs de la pression dans les éléments voisins. Cette méthode est efficace et précise : elle permet de maintenir le temps de calcul dans des limites raisonnables.
Pour une timbale de 50 centimètres de hauteur et de 60 centimètres de diamètre, on construit un maillage de quelques centaines de facettes triangulaires. L’instrument virtuel est plongé dans un domaine cubique de un mètre de côté, subdivisé en 64 000 cubes élémentaires. Il faut alors 72 000 pas de temps, soit environ deux heures de calculs pour simuler trois secondes de son ! Les sons synthétisés de cette façon ressemblent aux sons produits par un instrument réel. La forme des ondes de pression calculées et celle des ondes mesurées en plaçant un microphone à dix centimètres au-dessus d’une timbale réelle sont presque identiques.
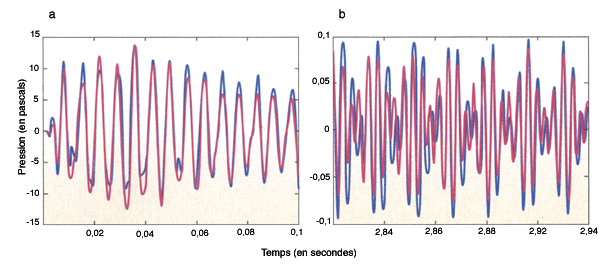
Les formes de l’onde de pression calculées (en bleu) et mesurées à l’aide d’un microphone placé à dix centimètres au-dessus d’une timbale réelle (en rouge) sont presque identiques. La correspondance est parfaite, aussi bien au cours des 100 premières millisecondes (a) qu’après trois secondes (b), alors que le son est déjà quasi inaudible. Cela signifie que la reproduction du son par le modèle numérique mis au point par les auteurs est fidèle jusque dans des détails que l’oreille humaine peut à peine percevoir.
Les simulations qui décrivent leur évolution respective dans le temps sont presque exactement superposables au son réel, aussi bien au début de l’établissement du son que lors de son extinction. Une preuve que la reproduction est fidèle jusque dans des détails que l’oreille humaine peut à peine percevoir…
D’autres analyses confirment la qualité du son simulé de façon plus spectaculaire encore. Un son quelconque n’a pas de période bien définie. Il peut toutefois être considéré comme une superposition d’ondes sinusoïdales de fréquences données. L’analyse spectrale d’un son est analogue à la décomposition de la lumière blanche en différentes couleurs : elle consiste à décomposer le son en ses constituants sinusoïdaux « purs ». Le spectre du son considéré apparaît alors sous la forme de raies de fréquences différentes, dont la hauteur représente l’amplitude (ou l’énergie) des ondes sinusoïdales correspondantes. Le spectre du son produit à l’aide d’une timbale réelle comporte sept à huit raies principales très fines et à peu près régulièrement espacées, dont certaines sont dédoublées. D’autres raies, de plus faible amplitude, apparaissent entre ces dernières. Le spectre du son simulé présente des raies d’amplitude et de position presque identiques.
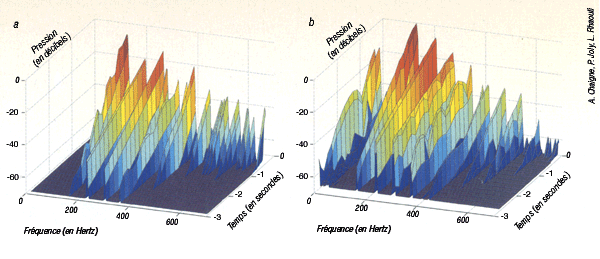
Le spectre du son de la timbale simulée (a) et celui de la timbale réelle (b) sont constitués de sept à huit raies intenses de fréquence presque identiques. Au cours de l’atténuation du son, certaines raies dédoublées décroissent en oscillant. Ces battements, que l’on peut distinguer à l’oreille, sont dus à des va-et-vient de l’énergie acoustique entre deux raies de fréquences très proches. Le modèle a révélé que ce phénomène est dû à une répartition non homogène de la tension de la peau sur le fût de la timbale.
On peut également suivre l’évolution dans le temps des différentes raies qui composent un son. L’énergie de vibration de l’instrument est évacuée par les ondes sonores et dissipée dans le matériau de la membrane. Le son s’atténue et devient inaudible environ trois secondes après l’impact. Bien que le contenu spectral soit très riche au moment de l’établissement du son, on constate – dans le son simulé comme dans le son réel – que le son de la timbale en cours d’extinction ne comporte plus que quelques raies. Ces raies sont toutes des multiples d’une fréquence dite « fondamentale » (présente ou non dans le spectre initial).
Un son composé de raies de fréquences multiples les unes des autres est dit « harmonique », et la sensation de hauteur qu’il provoque est nette. En revanche, au moment de l’attaque, on ne peut distinguer véritablement de raies dans le spectre du son de la timbale (le spectre est continu). Le son correspondant est un bruit sans hauteur bien nette. L’étude de l’atténuation des raies du spectre de la timbale montre comment la plupart des instruments de percussion produisent des sons qui ne deviennent harmoniques qu’en cours d’extinction. Par ailleurs, au cours de l’atténuation, les différentes composantes du son évoluent différemment. Certaines diminuent de façon régulière, d’autres subissent des oscillations assez prononcées, perceptibles sous forme de battements. Notre modèle nous a permis de vérifier qu’il fallait introduire une tension irrégulière de la peau pour synthétiser un son présentant les mêmes battements que le son enregistré. L’étude de l’atténuation du son virtuel illustre comment une simulation fine des phénomènes acoustiques nous permet de préciser les fondements physiques des sensations auditives provoquées par le son d’un instrument.
En disposant d’un modèle précis d’instrument, on peut étudier les effets acoustiques de variations infinitésimales de la géométrie d’un instrument ou des propriétés des matériaux qui le composent, ce qui serait presque impossible avec des instruments réels. Avec cet outil, on étudie également comment les perceptions auditives transmettent une information sur les processus qui engendrent les sons, informations dont nous tirons instinctivement profit pour évaluer notre environnement (par exemple, dans l’obscurité, il suffit parfois de tapoter légèrement la surface d’un objet pour que le son émis nous renseigne sur le type de matériau dont il est fait ou sur la présence d’une cavité).
Enfin, les calculs seront peut-être un jour assez rapides pour rendre possible la synthèse de sons en temps réel. On verra alors un percussionniste frapper des coussinets sensibles reliés à un ordinateur commandant un programme de synthèse sonore fondé sur un modèle physique de timbale. L’ordinateur délivrera alors une cascade de roulements, conférant à n’importe quel timbalier, une virtuosité encore inaccessible aujourd’hui.
Quelques références vous sont proposées pour en savoir plus sur les modélisations de la timbale.
En français
- Leïla Rhaouti, Antoine Chaigne et Patrick Joly, Modélisation numérique de la timbale (vidéo réalisée par Arghyro Paouri, produite par l’INRIA Multimédia), 1998.
- Ouvrage collectif, Les instruments de l’orchestre, Éditions Belin-Pour la Science, 1995.
- Jean-François Zygel, La leçon de musique de Jean-François Zygel – Haydn les clefs de l’orchestre, DVD chez Naïve.
En anglais
- Virginia Tech Music Department
- Percussion instrument
- Neville Fletcher et Thomas Rossing, Physics of musical instruments, Springer, 1998.
- Leïla Rhaouti, Antoine Chaigne et Patrick Joly, Time-domain modeling and numerical simulation of a kettledrum, in Journal of the Acoustical Society of America, vol. 105 (6), pp. 3545-3562, 1999.
Une première version de cet article est parue dans le dossier n°52 La modélisation informatique, exploration du réel de la revue Pour la Science, numéro de juillet/septembre 2006.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Antoine Chaigne
Responsable de l'unité d'enseignement et de recherche en mécanique ENSTA-UME.

Leïla Rhaouti