
Les réseaux bayésiens
Depuis leur introduction par Judea Pearl en 1988, les réseaux bayésiens sont devenus un outil extrêmement populaire en intelligence artificielle pour modéliser ces incertitudes et pour les exploiter dans la prise de décision. Plus précisément, ils permettent de représenter de manière très compacte sur ordinateur des probabilités et ils fournissent les clefs pour calculer efficacement celles utiles à la prise de décision.
De la bicyclette aux probabilités jointes
Lorsque l’on est confronté à un problème de décision en présence d’incertitudes, il convient en premier lieu d’identifier les facteurs incertains. Imaginons que vous devez vous rendre à votre travail et vous vous demandez si vous avez intérêt à y aller à bicyclette. Lorsqu’il n’y a pas trop de pollution, c’est plutôt un trajet agréable mais lorsqu’il y en a, cela vous provoque des crises d’asthme, que vous souhaitez éviter. Le niveau de pollution est donc une variable entrant en jeu dans votre décision de prendre ou non votre vélo. On ne connaît jamais exactement la valeur de cette variable (c’est-à-dire le niveau précis de pollution). C’est donc un facteur incertain, ce que l’on appelle généralement en mathématiques une « variable aléatoire ». Une telle variable peut prendre différentes valeurs, certaines ayant plus de chances d’arriver que d’autres. Par exemple, en Île de France, d’après les données d’AirPARIF (voir l’histogramme ci-dessous), si la variable « pollution » correspond à l’indice atmo, celle-ci peut prendre des valeurs de 1 à 10, mais on peut constater qu’il y a beaucoup plus de chances que le niveau de pollution se situe aux alentours de 3 ou 4 plutôt qu’à 1 ou 10. Si vous passez votre souris sur l’histogramme, vous observerez le nombre de jours où la pollution a atteint chaque niveau en 2016.
On peut donc associer à la variable aléatoire « pollution » une « distribution de probabilité », c’est-à-dire une fonction qui associe à chaque niveau ou indice de pollution son pourcentage de chance d’arriver. Généralement, on note cette fonction \(P(\)pollution\()\), en mettant entre parenthèses le nom de la variable aléatoire. Ici, on peut représenter cette fonction par le tableau suivant :
| distribution de probabilité de la variable pollution : |
Chacun des nombres de la colonne de droite est appelé une « probabilité ». Par exemple, le 0,4235 ou 42,35% de la troisième ligne est la « probabilité que le niveau de pollution soit égal à 3 ». (Attention à ne pas confondre la « probabilité », qui est un nombre, avec la « distribution de probabilité » de pollution qui, elle, est une fonction, pas un nombre.)
Pour déterminer la distribution \(P(\)pollution\()\), il suffit de compter, pour chaque niveau de pollution, le nombre de jours où ce niveau a été atteint et diviser ce dernier par le nombre de jours de l’année (de sorte que la somme de toutes les probabilités soit égale à 100 % : il y a 100 % de chances que le niveau de pollution soit compris entre 1 et 10).
De la même manière, on peut créer une variable aléatoire « asthme » indiquant si l’on a une crise d’asthme ou non : il s’agit donc d’une variable à deux valeurs (« crise », « pas de crise ») dont on peut déterminer la distribution de probabilité en comptant le nombre de jours dans l’année où l’on a eu une crise (ou pas) et en le divisant par le nombre de jours de l’année.
Prises isolément, ces deux variables ne sont pas très intéressantes pour votre prise de décision. En effet, c’est parce qu’il y a de la pollution que vous risquez une crise d’asthme. Il existe donc une relation, une corrélation, entre ces deux variables et c’est précisément au travers de cette corrélation que vous allez pouvoir prendre votre décision : grossièrement, lorsqu’il y a de la pollution, vous risquez une crise et vous devez éviter de prendre votre vélo. Il est donc intéressant d’exploiter, non pas la distribution de probabilité de l’une ou l’autre des variables, mais leur « distribution de probabilité jointe », c’est-à-dire la fonction de deux variables \(P(\)asthme, pollution\()\) qui associe à chaque niveau possible de pollution et chaque état possible de l’asthme une probabilité. Le tableau ci-dessous représente une telle distribution : la deuxième colonne contient ainsi les probabilités \(P(\)pollution = niveau, asthme = crise\()\), la troisième colonne contient les probabilités \(P(\)pollution = niveau, asthme = pas de crise\()\) et la somme de tous ces pourcentages est égale à 100 %.
| distribution de probabilité jointe de pollution et d’asthme : |
Grâce à cette table, on sait qu’il y a 34,00 % de chances d’avoir en même temps une pollution de niveau 3 et pas de crise d’asthme et qu’il y a 8,35 % de chances d’avoir en même temps une pollution de niveau 3 et une crise d’asthme.
Imaginons maintenant qu’on sache que le niveau de pollution vaut 3. On peut alors calculer une nouvelle distribution de probabilité de la variable « asthme » sachant que la pollution est de niveau 3. En appliquant cette notion à tous les niveaux de pollution, on obtient la distribution de probabilité d’asthme conditionnellement à pollution, ce que l’on note \(P(\mbox{asthme}|\mbox{pollution})\). À droite du signe « | », on met toutes les informations dont on dispose.
Pour calculer ces probabilités conditionnelles, on utilise la formule
\begin{equation} P(\mbox{asthme},\mbox{pollution}) = P(\mbox{pollution}) \times P(\mbox{asthme}|\mbox{pollution}). \label{eq:AetP} \end{equation}
L’interprétation de cette formule est intéressante et relativement intuitive : pour obtenir la probabilité d’avoir une crise d’asthme et un niveau de pollution donné, on multiplie la probabilité d’avoir ce niveau de pollution par la probabilité d’avoir la crise d’asthme sachant que l’on a atteint ce niveau.
Cette formule n’est pas limitée à « asthme » et « pollution » : quelles que soient les variables ou ensembles de variables \(X\) et \(Y\), on a toujours \(P(X,Y) = P(Y) \times P(X|Y)\).
Pour calculer les probabilités conditionnelles (en pourcentage) de « asthme », sachant que la pollution est de niveau 3, on fait une simple règle de trois, pour obtenir le nombre de cas avec crise et le nombre de cas sans crise, lorsqu’il y a 100 cas de pollution de niveau 3 :
\begin{equation} \left\{ \begin{array}{l} P(\mbox{asthme=crise}|\mbox{pollution=3})= \frac{34}{42,35} \times 100 = 80,28 \%, \\ P(\mbox{asthme=pas de crise}|\mbox{pollution=3}) = \frac{8,35}{42,35} \times 100 = 19,72 \%. \end{array} \right. \label{eq:AcondP2} \end{equation} Les probabilités conditionnelles, nombres entre 0 et 1, sont donc obtenues par simple division : \begin{equation} \left\{ \begin{array}{l} P(\mbox{asthme=crise}|\mbox{pollution=3}) = \frac{P(\mbox{asthme=crise},\mbox{pollution=3})}{P(\mbox{pollution=3})}, \\ P(\mbox{asthme=pas de crise}|\mbox{pollution=3}) = \frac{P(\mbox{asthme=pas de crise},\mbox{pollution=3})}{P(\mbox{pollution=3})}. \end{array} \right. \label{eq:AcondP3} \end{equation}
On a bien une nouvelle distribution de probabilité, avec la somme des probabilités qui vaut 1.
Calculer la probabilité conditionnelle \(P(\mbox{asthme}|\mbox{pollution})\) revient à diviser chaque ligne de la table ci-dessus par la probabilité du niveau de pollution de la ligne (qui est la somme des nombres de la ligne) pourvu, évidemment, que cette probabilité soit non nulle. La somme des pourcentages de chaque nouvelle ligne ainsi obtenue est donc égale à 100%. En effet, sachant le niveau de pollution, il y a 100% de chances d’avoir ou de ne pas avoir une crise d’asthme. Lorsque la probabilité du niveau de pollution de la ligne est nulle, comme c’est le cas ici pour le niveau 1 de pollution, on ne peut pas effectuer la division, mais, dans ce cas, on peut affecter n’importe quelles probabilités à \(P(\mbox{asthme=crise}|\mbox{pollution=1})\) et \(P(\mbox{asthme=pas de crise}|\mbox{pollution=1})\), pourvu que la somme de ces deux probabilités soit égale à 100%. Ici, on choisit une probabilité faible d’avoir une crise lorsque la pollution est faible. On obtient donc :
| distribution de probabilité d’asthme conditionnellement à pollution : |
De la pollution aux variables indépendantes
Supposons que vous n’ayez pas toujours accès à l’information sur le niveau de pollution (par exemple, parce que, temporairement, vous n’avez pas accès à internet et que vous ne pouvez donc pas consulter le site d’AirPARIF). Dans ce cas, les distributions ci-dessus ne pourront pas vous aider dans votre prise de décision. Aussi peut-il être intéressant de rajouter des variables aléatoires pour décrire de manière plus générale votre problème de décision. Ainsi, on peut remarquer que le niveau de pollution dépend de la densité du « trafic » routier. Or, vous écoutez peut-être une radio qui vous donne une telle information. Si vous n’y avez pas accès, vous pouvez observer si c’est l’« heure » de pointe ou non, car celle-ci vous donne de précieuses informations sur le « trafic ». De même, si votre voisin vous dit qu’il a entendu qu’il y avait un « accident » sur le trajet que vous planifiez de prendre, cela peut engendrer des embouteillages et donc une densité de « trafic » élevée. Enfin, si vous observez par votre fenêtre que la « météo » est mauvaise, même si vous n’avez pas vu votre volubile voisin, vous pouvez en déduire qu’il y a des chances non négligeables pour qu’un accident ait lieu. Il vous faut donc construire la distribution de probabilité jointe de toutes ces variables :
\begin{equation} P(\mbox{asthme},\mbox{pollution},\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo}). \label{eq:Ajoint} \end{equation}
Malheureusement, ce calcul pose un véritable problème : la taille de la table correspondante est égale au produit du nombre de valeurs possibles de chacune des variables aléatoires. Ainsi, vous pouvez constater que la distribution jointe d’asthme et de pollution correspond à une table de \(10 \times 2 = 20\) nombres. Si l’on suppose que :
- « trafic » a 4 valeurs possibles (faible, habituel, chargé, exceptionnel), comme sur le site d’information sytadin,
- « heure » a 24 valeurs (de 0 à 23 h),
- « accident » a deux valeurs : oui, non,
- « météo » a cinq valeurs (beau temps, nuageux, pluvieux, orageux, neigeux),
alors \(P(\mbox{asthme},\mbox{pollution},\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo})\) correspond à une table de \(2 \times 10 \times 4 \times 24 \times 2 \times 5 = 19200\) nombres. On peut aisément stocker autant de nombres sur ordinateur, mais si l’on rajoute encore de nouvelles variables, on arrive rapidement à une situation où la mémoire de l’ordinateur devient insuffisante pour ce stockage. C’est le cas, par exemple, lorsque la General Electric diagnostique les problèmes de performances de ses moteurs d’avions CF6 dont sont équipés certains Boeings (cf. l’image ci-dessous). On imagine aisément que de nombreux facteurs entrent en jeu dans l’estimation de cette performance (état des valves d’admission, etc.) et, effectivement, le nombre de combinaisons possibles de leurs valeurs excède 10105. Ceci implique que la distribution de probabilité jointe employée devrait nécessiter une capacité de stockage de plus de 10105 octets, ce qui dépasse largement celle de tous les ordinateurs du monde réunis.

Moteur CF6 (Source : wikipedia)
De plus, même si l’on peut stocker sur n’importe quel ordinateur moderne 19200 nombres, encore faut-il être capable de déterminer quels nombres on doit stocker. Quand nous avons vu la distribution de probabilité de « pollution » en début de cet article, celle-ci avait été déterminée en observant l’historique des mesures de niveaux de pollution sur une année. Pour obtenir des nombres relativement fiables, on considère habituellement que, dans cet historique, il faut au moins 10 fois plus de mesures que le nombre de cases que contient la table de la distribution de probabilité. Si celle-ci possède 19200 cases, il faut donc un historique d’au moins 192000 mesures, c’est-à-dire un historique créé sur une période de 21 ans si l’on effectue une mesure de chacune des variables toutes les heures. C’est tout de même trop fastidieux pour être utilisable en pratique.
Fort heureusement, en exploitant une propriété d’indépendance, on peut arriver à réduire drastiquement le nombre de mesures nécessaires. En probabilités, deux variables sont dites « indépendantes » si quelle que soit l’information que l’on a sur l’une, cela ne nous donne aucune information sur l’autre : si deux variables aléatoires ou ensembles de variables \(X\) et \(Y\) sont indépendantes, alors la probabilité de \(X\) quand on connaît \(Y\) est la même que celle de \(X\) sans connaissance de \(Y\), autrement dit \(P(X|Y) = P(X)\). La probabilité jointe de deux variables indépendantes \(X\) et \(Y\) est donc le produit de leurs probabilités : \(P(X,Y) = P(Y) P(X)\).
On met à droite du signe « | » toutes les connaissances que l’on a. Par conséquent, si l’indépendance entre \(X\) et \(Y\) n’est avérée que lorsque l’on connaît une autre variable \(Z\), alors on dit que \(X\) et \(Y\) sont indépendantes conditionnellement à \(Z\) et la probabilité de \(X\) conditionnellement à \(Y\) et \(Z\) est égale à la probabilité de \(X\) conditionnellement à \(Z\) : \(P(X|Y,Z) = P(X|Z)\).
Du vélo aux réseaux bayésiens
Maintenant, on peut combiner les probabilités jointes et l’indépendance conditionnelle pour obtenir enfin un modèle utilisable en pratique pour la prise de décision. On peut décider dans le modèle que l’« asthme » dépend de la pollution, mais que, quand on connaît le niveau de pollution, les autres variables n’apportent plus aucune nouvelle information utile. Dans ce cas, conditionnellement à « pollution », « asthme » est indépendante des autres variables. De même, on peut choisir que la « pollution » dépend uniquement du « trafic », que l’état du « trafic » dépend de l’heure (notamment du fait que l’on soit ou non en heure de pointe) et du fait qu’il y a ou non un « accident », et qu’« accident » dépend de la « météo ».
On peut créer un modèle graphique, plus visuel, qui représente la décomposition que nous avons obtenue.
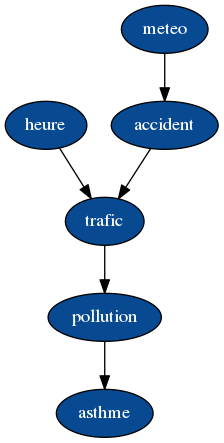
Le réseau bayésien pour décider si l’on utilise son vélo.
Dans ce graphe, les nœuds représentent les variables aléatoires, « asthme », « pollution », etc. et chaque probabilité conditionnelle est représentée par des flèches (on parle aussi d’arcs). Par exemple, \(P(\mbox{trafic}|\mbox{heure},\mbox{accident})\) est représenté par une flèche de « heure » vers « trafic » et une flèche de « accident » vers « trafic ». De plus, si l’on associe à chaque nœud sa distribution de probabilité conditionnellement à ses parents dans le graphe (par exemple on associe à « trafic » la distribution \(P(\mbox{trafic}|\mbox{heure},\mbox{accident})\)), on obtient ce que l’on appelle un réseau bayésien.
Un réseau bayésien est donc un modèle graphique probabiliste dans lequel les nœuds représentent des variables aléatoires et la distribution de probabilité jointe de toutes ces variables s’exprime comme le produit des distributions de chaque nœud/variable conditionnellement à ses parents. Toute absence d’arc entre deux nœuds représente une indépendance conditionnelle probabiliste.
En appliquant les formules de probabilités jointes et de probabilités conditionnelles, on obtient
\begin{equation} \begin{array}{lcl} P(\mbox{asthme},\mbox{pollution},\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo}) \\= P(\mbox{asthme}|\mbox{pollution}) \times P(\mbox{pollution}|\mbox{trafic}) \times P(\mbox{trafic}|\mbox{heure},\mbox{accident}) \times P(\mbox{heure}) \\
\times P(\mbox{accident}|\mbox{météo}) \times P(\mbox{météo}). \end{array} \label{eq:rb} \end{equation}
On a
\begin{array}{l} P(\mbox{asthme},\mbox{pollution},\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo}) \\ = P(\mbox{asthme}|\mbox{pollution}) \times P(\mbox{pollution},\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo}) \\ P(\mbox{pollution},\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo}) = P(\mbox{pollution} | \mbox{trafic}) \times P(\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo}) \\ P(\mbox{trafic},\mbox{heure},\mbox{accident},\mbox{météo}) = P(\mbox{trafic} | \mbox{heure},\mbox{accident}) \times P(\mbox{heure},\mbox{accident},\mbox{météo}) \\ P(\mbox{heure},\mbox{accident},\mbox{météo}) = P(\mbox{heure}) \times P(\mbox{accident},\mbox{météo}) \\ P(\mbox{accident},\mbox{météo}) = P(\mbox{accident} | \mbox{météo}) \times P(\mbox{météo}) \end{array}
L’avantage de cette décomposition est que l’on remplace une « grosse » distribution de probabilité jointe (de 19200 cases) par plusieurs « petites » distributions de probabilité conditionnelles (de, respectivement, 20, 40, 192, 24, 10 et 5 cases). On n’a donc plus besoin de faire des mesures chaque heure pendant 21 ans pour remplir ces tables, une seule année suffit amplement.
Le réseau représentant une distribution jointe, on peut l’interroger pour calculer des probabilités. Les réseaux bayésiens s’avèrent particulièrement utiles car on peut utiliser la décomposition qu’ils encodent afin d’accélérer significativement les calculs.
Par exemple, supposons que vous observiez que « météo » a pour valeur « nuageux » et que votre montre vous indique que « heure » a pour valeur 8h. Dans ce cas, votre décision de prendre votre vélo dépend de la distribution de probabilité d’« asthme » conditionnellement à « météo »=nuageux et « heure »=8h, autrement dit \(P(\mbox{asthme}|\mbox{heure}=8h,\mbox{météo}=nuageux)\). En utilisant le réseau asthme, avec le logiciel pyAgrum, on obtient le résultat après 1,26ms de calcul.
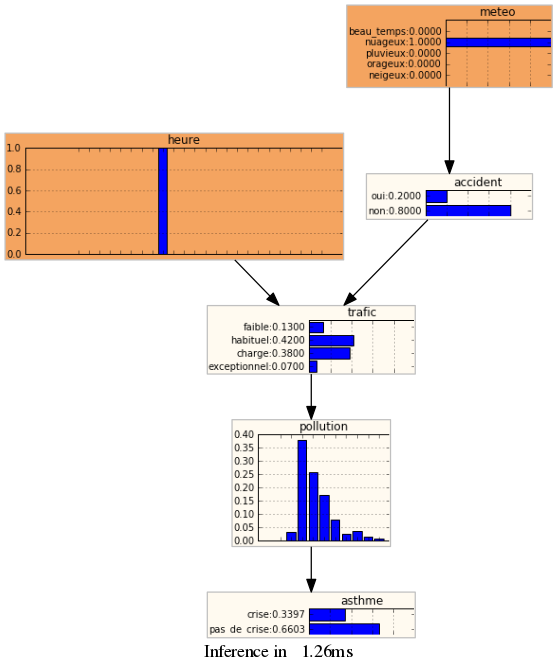
Les distributions de probabilité des variables sachant que « heure » = 8 h et « météo » = nuageux.
On voit que l’on a ici environ 34% de chances d’avoir une crise d’asthme lorsque « heure »= 8h et « météo »= nuageux. Si vous souhaitez effectuer d’autres calculs dans ce réseau, vous pouvez télécharger le notebook python/pyAgrum dont sont extraites les images ci-dessus.
Nous avons vu plus haut que, quelles que soient les variables ou ensembles de variables \(X\) et \(Y\), on a \(P(X,Y) = P(Y) \times P(X|Y)\), ce qui revient à \(P(X|Y) = P(X,Y) / P(Y)\).
En posant \(X = \mbox{asthme}\) et \(Y = \{\mbox{heure},\mbox{météo}\}\), on obtient donc :
\begin{equation}
P(\mbox{asthme}|\mbox{heure},\mbox{météo}) =
\frac{P(\mbox{asthme},\mbox{heure},\mbox{météo})}{P(\mbox{heure},\mbox{météo})}.
\end{equation}
Ici, on ne s’intéresse pas à n’importe quelle heure ni à n’importe quelle météo, mais seulement à 8h et à une météo nuageuse. On veut donc calculer \(P(\mbox{asthme}|\mbox{heure}=8h,\mbox{météo}=nuageux)\). D’après ce que l’on vient de voir, cela revient à calculer :
\begin{equation}
P(\mbox{asthme}|\mbox{heure}=8h,\mbox{météo}=nuageux) = \frac{P(\mbox{asthme},\mbox{heure}=8h,\mbox{météo}=nuageux)}{P(\mbox{heure}=8h,\mbox{météo}=nuageux)}.
\end{equation}
Si notre réseau bayésien avait encodé la distribution \(P(\mbox{asthme},\mbox{heure},\mbox{météo})\), obtenir le numérateur de cette fraction aurait été aisé : il aurait simplement fallu extraire de la table de probabilité jointe la ligne correspondant à \(\mbox{heure}=8h,\mbox{météo}=nuageux\). Malheureusement, le réseau bayésien représente une distribution jointe qui contient des variables supplémentaires : « pollution », « trafic » et « accident ». On voit donc qu’il faut « supprimer » ces variables de la distribution jointe du réseau bayésien.
Pour comprendre comment supprimer des variables d’une distribution jointe, prenons un exemple : supposons que nous souhaitions calculer \(P(\mbox{pollution})\) à partir de la distribution \(P(\mbox{pollution},\mbox{asthme})\). On comprend bien que le nombre de jours où le niveau de pollution est égal à 3 est la somme du nombre de jours où il est égal à 3 et où, en même temps, vous avez une crise d’asthme, et du nombre de jours où le niveau de pollution est égal à 3 et où, en même temps, vous n’avez pas de crise. Dans la table de la distribution jointe \(P(\mbox{pollution},\mbox{asthme})\), cela revient à additionner les pourcentages de la ligne « pollution = 3 ». Traduit en termes de probabilités, pour supprimer la variable \(\mbox{asthme}\) de la distribution \(P(\mbox{pollution},\mbox{asthme})\), il faut sommer les probabilités de la distribution jointe sur toutes les valeurs de \(\mbox{asthme}\), autrement dit :
\begin{equation}
P(\mbox{pollution}) = \sum_{\mbox{asthme}} P(\mbox{pollution},\mbox{asthme}).
\end{equation}
Cette technique est générale : pour supprimer des variables d’une distribution jointe, il suffit de sommer les probabilités de la distribution jointe sur toutes les valeurs des variables que l’on souhaite supprimer. Ainsi, dans le cas qui nous intéresse pour notre prise de décision :
\begin{equation}
\begin{array}{lcl}
P(\mbox{asthme},\mbox{heure}=8h,\mbox{météo}=nuageux) \\ = \sum_{\mbox{pollution}}\sum_{\mbox{trafic}}\sum_{\mbox{accident}} P(\mbox{asthme},\mbox{pollution},\mbox{trafic},\mbox{heure}=8h,\mbox{accident},\mbox{météo}=nuageux)
\end{array}
\end{equation}
et
\begin{equation}
P(\mbox{heure}=8h,\mbox{météo}=nuageux) = \sum_{\mbox{asthme}}
P(\mbox{asthme},\mbox{heure}=8h,\mbox{météo}=nuageux).
\end{equation}
En effectuant des multiplications, des divisions et des additions, vous pouvez donc vous servir de la distribution de probabilité jointe pour décider, quelles que soient les informations à votre disposition, si vous allez vous rendre à votre travail à vélo ou non. Les réseaux bayésiens réalisent ces calculs d’une manière très efficace. Notamment, il existe des algorithmes très perfectionnés pour réaliser les sommations mentionnées ci-dessus.
Conclusion
Les réseaux bayésiens sont des représentations compactes de distributions de probabilité de grandes tailles. Ils sont dotés d’algorithmes d’inférence très efficaces, pour calculer des distributions de probabilités a posteriori (c’est-à-dire sachant les informations à disposition) utiles à la prise de décision. Les réseaux bayésiens permettent également de déterminer efficacement l’instanciation, c’est-à-dire la valeur de l’ensemble de toutes les variables ayant la plus forte probabilité, ce que l’on appelle « l’explication la plus probable », ou bien l’instanciation d’un sous-ensemble de variables ayant la plus forte probabilité, ce que l’on appelle « maximum a posteriori ».
La profusion d’algorithmes permettant de construire automatiquement ces réseaux à partir de bases de données (SQL ou fichiers Excel) ainsi que les nombreux algorithmes d’inférence très efficaces ont fait des réseaux bayésiens un modèle incontournable quand on souhaite calculer des probabilités. C’est ce qui explique pourquoi les réseaux bayésiens sont exploités dans de nombreux domaines, allant du médical (diagnostic de maladies potentiellement rares, surveillance de patients) à l’assurance (détection de fraudes), en passant par l’énergie (prédictions de consommations), la cybersécurité (détection d’intrusions), l’automobile (géolocalisation de voitures autonomes), l’imagerie (suivi de personnes dans des séquences vidéo), etc.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Christophe Gonzales