Les systèmes de recommandation favorisent-ils la diversité ?

Les réseaux en ligne et les plates-formes de streaming sont devenus très présents dans notre vie quotidienne. La plupart d’entre nous les utilisent pour acheter des produits, pour s’informer, pour écouter de la musique, regarder des films… et ce de manière massive. Songez que chaque année, plus de 20 millions de produits sont achetés via la plate-forme Amazon, que près de 500 millions de messages sont relayés quotidiennement sur Twitter, qu’environ 3 milliards d’individus s’informent via Facebook et que plus de 5 milliards de vidéos sont visionnées chaque jour…

Ces chiffres peuvent donner le vertige mais ils révèlent surtout la quantité de données que les plates-formes ont à gérer au quotidien. C’est pourquoi celles-ci ont mis au point des algorithmes dits « de recommandation » dont le but est d’organiser ces contenus et d’en filtrer un très grand nombre afin de n’en proposer que quelques-uns à chaque internaute, en fonction bien sûr de son goût et de ses habitudes.

Si les systèmes de recommandation ont ainsi proliféré ces vingt dernières années, les algorithmes sur lesquels ils reposent ont commencé récemment à faire face à des critiques, plus ou moins virulentes, sur leurs effets indirects. Ils sont ainsi régulièrement mis en cause dans l’apparition de phénomènes d’enfermement sur les réseaux sociaux et la propagation de fausses informations.

Illustration 1 © Sacha Berna.

Mais comment mesurer proprement ces effets ?

Nous allons voir comment étudier la diversité des recommandations en faisant le lien entre graphes, marches aléatoires, distributions de probabilité et mesures d’entropie…

Graphes tripartis

Prenons le cas d’une plate-forme de streaming sur laquelle les internautes peuvent écouter de la musique, soit en allant chercher une chanson en particulier, soit en suivant les recommandations faites par la plate-forme. La question que l’on se pose est de savoir comment caractériser ces écoutes en terme de diversité.

Comme souvent en recherche, tout commence par comprendre de quelles informations on dispose et comment elles se présentent. En l’occurrence ici, la première information dont disposent les plates-formes pour identifier les centres d’intérêt des internautes, c’est leur profil d’écoute, c’est-à-dire quel titre a été écouté, par qui, quand et combien de fois. Cette information traduit donc une relation entre des utilisateurs et des chansons. Or quoi de mieux pour représenter des relations qu’un graphe ? Et même plus précisément un graphe biparti pondéré, c’est-à-dire un graphe dans lequel les sommets sont répartis en deux ensembles disjoints (les utilisateurs d’un côté et les musiques de l’autre) et les liens relient les utilisateurs aux musiques qu’ils ont écoutées par le passé, avec un poids traduisant le nombre d’écoutes.

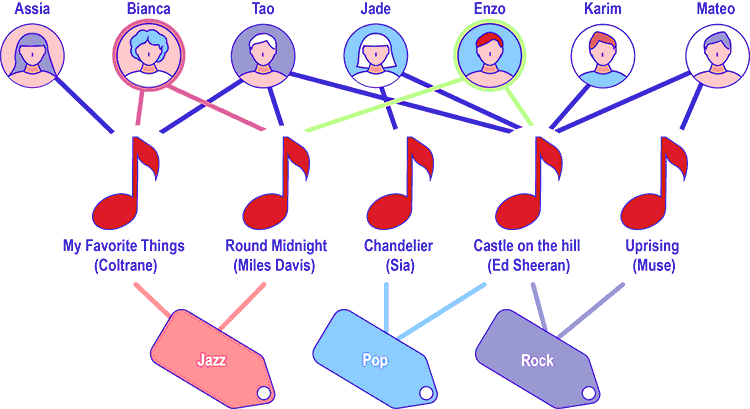
Mais les plates-formes disposent également d’autres informations, notamment des métadonnées sur les titres musicaux. Pour faire simple considérons uniquement ici les genres musicaux auxquels appartiennent les chansons (rock, rap, métal, jazz…). On voit alors apparaître un second graphe, biparti lui aussi (et éventuellement pondéré), qui relie des chansons à des catégories musicales. Au final, on a donc affaire à un graphe triparti, dans lequel des utilisateurs (premier niveau) écoutent des chansons (second niveau) associées à des catégories (troisième niveau), comme sur l’exemple suivant.

Illustration 2 © Sacha Berna.

Marche aléatoire

La question devient alors de déterminer comment exploiter ce graphe triparti pour exprimer la notion de diversité que l’on cherche à capturer ? Plus précisément, il s’agit de réussir à relier les utilisateurs à leurs univers musicaux de manière à refléter le poids relatif de ces univers dans leur profil d’écoute.

Pour ce faire, une idée simple (mais efficace !) consiste à parcourir ce graphe de manière aléatoire : partant d’un sommet « utilisateur », on se dirige vers les catégories musicales en choisissant aléatoirement le prochain sommet en fonction des liens (éventuellement pondérés) présents dans le graphe. Ceci permet donc de relier les utilisateurs aux différents univers musicaux à l’aide du niveau intermédiaire que constituent les chansons écoutées par ces derniers. L’idée est que plus une catégorie musicale est au centre du profil d’écoute de l’utilisateur, plus une marche aléatoire partant de cet utilisateur va nous ramener vers cette catégorie. En systématisant cette démarche, on peut alors déterminer la distribution de probabilité d’atteindre les différentes catégories à partir des utilisateurs.

Pour mieux comprendre, comparons le cas de Bianca et celui d’Enzo de l’illustration 2. Bien que tous deux écoutent exactement deux titres musicaux (on suppose ici que le graphe est non pondéré pour simplifier), leur profil d’écoute est très différent en termes de diversité et cela est bien capturé par les marches aléatoires. Ainsi, si on considère une marche aléatoire partant de Bianca, celle-ci a une chance sur deux de passer par le titre My Favorite Things et une chance sur deux de passer par Round Midnight. Mais quel que soit le chemin pris, ces deux titres vont tous deux mener au même univers musical, le Jazz. La distribution de probabilité sur les univers Jazz / Pop / Rock est donc de \(1 / 0 / 0\).

En revanche, partant d’Enzo, une marche aléatoire peut mener soit à Round Midnight, soit à Castle on the hill. Dans le premier cas, le chemin terminera à l’univers Jazz, mais dans le second cas, le chemin donne un nouvel embranchement pouvant mener à l’univers Pop, ou bien Rock. Au final, la distribution est cette fois-ci de \(0,5 / 0,25 / 0,25\), ce qui traduit un profil un peu plus équilibré que celui de Bianca.

Diversité

On a donc une méthode permettant de caractériser, sous forme de distribution, l’univers musical d’un utilisateur à partir du graphe décrivant ses écoutes, mais cela ne nous dit rien de précis encore sur la diversité en elle-même…

Nous ne sommes cependant plus très loin et le cas de Bianca et Enzo nous permet de préciser ce que l’on entend en réalité par diversité. L’intuition forgée par cet exemple est que le profil d’écoute d’Enzo est plus diversifié que celui de Bianca car, bien qu’ils soient tous deux reliés au même nombre de chansons, Enzo a une écoute plus équilibrée que Bianca en termes de genres musicaux.

Reste à déterminer comment mesurer à quel point une distribution (par exemple issue d’une marche aléatoire sur un graphe…) est équilibrée, c’est-à-dire à quel point une distribution est proche d’une répartition uniforme dans laquelle toutes les catégories auraient la même proportion, c’est-à-dire \( \frac{1}{3} / \frac{1}{3} / \frac{1}{3} \) dans notre exemple.

Pour ce faire, on peut par exemple calculer l’indice de diversité suivant. Étant donnée une distribution de probabilité \(p=( p_1, p_2, \ldots, p_k )\) où \(p_i\) traduit ici la probabilité qu’une marche aléatoire termine sur le sommet \(i\), on définit l’indice de diversité (d’ordre \(\alpha\)) par : \[D_{\alpha} (p) = \left( \sum_{i=1}^k p_i^{\alpha} \right) ^ {\frac{1}{1 – \alpha}} \]

Reprenons l’exemple précédent pour se faire une idée, en se focalisant sur \(\alpha=2\). En repartant des distributions observées précédemment, on peut déterminer que la diversité d’ordre 2 de Bianca est de \(1\) (\( \frac{1}{1^2 + 0^2 + 0^2} \) ) tandis que celle d’Enzo est de \(8/3\) ( \( \frac{1}{ (\frac{1}{2})^2 + (\frac{1}{4})^2 + (\frac{1}{4})^2 } \) ). Cette mesure reflète bien le fait qu’Enzo a un profil d’écoute plus diversifié que celui de Bianca.

Au-delà de cet exemple particulier, que peut-on dire de cet indice ?

Tout d’abord, remarquons que cet indice permet bien d’analyser la diversité de la distribution \(p\) vis-à-vis de la distribution parfaitement équilibrée, et ce quel que soit l’ordre de diversité choisi. En effet, si \(N\) est le nombre de catégories et \(p=( p_1, p_2, \ldots, p_N)\) est la distribution uniforme associée (c’est-à-dire telle que \(p_i= \frac{1}{N}\) pour tout \(i\)), alors quel que soit l’ordre \(\alpha \neq 1\), nous avons le développement suivant :

\[ D_{\alpha}(p) = \left( \sum_{i=1}^N \frac{1}{N^{\alpha}} \right) ^{\frac{1}{1-\alpha}} = \left( \frac{1}{N^{\alpha -1}} \right) ^ {\frac{1}{1-\alpha}} = \frac{1}{N^{-1}} = N\]

Au final, la valeur de \(D_{\alpha}(p)\) est donc comprise entre \(1\) (une seule catégorie accapare la distribution de probabilités) et \(N\) (les \(N\) catégories sont atteintes de manière uniforme), ce qui permet de positionner la valeur obtenue pour une distribution particulière \(p\) au regard de ces deux situations extrêmes. Nous pouvons donc préciser là encore les distributions obtenues pour Enzo et Bianca. Bianca obtient la plus petite valeur possible, ce qui correspond bien au fait que son univers musical est exclusivement concentré sur une catégorie, tandis qu’Enzo est très proche d’une diversité parfaite (\(3\) dans notre exemple), traduisant le fait qu’il est relié à toutes les catégories proposées, et ce de manière relativement bien équilibrée.

Au passage, notons également que la diversité d’ordre 2 prise dans l’exemple précédent n’est pas choisie au hasard. Elle est en lien direct avec un indice très connu des économistes, l’indice de Herfindahl-Hirschmann, utilisé notamment pour détecter des situations de monopole sur des marchés économiques. Diversité et monopole ne sont en fait que deux versants d’une même notion…

D’ailleurs, d’autres valeurs de \(\alpha\) correspondent également à des indices très connus. Le cas de la diversité d’ordre 1 est par exemple intéressant. Ce cas est bien sûr dégénéré puisque la définition de \(D_{\alpha}(p)\) présente une division par \(\alpha -1\), mais lorsque \(\alpha\) tend vers \(1\), \(D_{\alpha}(p)\) peut se réécrire en \[ 2 ^{ – \sum_{i=1}^k p_i \log(p_i)}\] qui n’est rien d’autre que l’exponentielle de l’entropie de Shannon, bien connue en informatique.

De même, la forme dégénérée de la définition pour \(\alpha = \infty\) correspond elle aussi à un indice connu. Elle se réécrit en effet en \( D_{\infty}(p) = \left( \max_i p_i \right)^{-1} \), qui est l’inverse de la proportion maximale observée parmi les \(p_i\). Or cette valeur est directement liée à l’indice de Berger-Parker (c’est simplement son inverse !), utilisé notamment dans les études sur la biodiversité des écosystèmes car il permet de mesurer à quel point l’espèce dominante est prépondérante vis-à-vis des autres espèces.

Quoi qu’il en soit des propriétés intrinsèques de cet indice et de ses relations avec les indices connus, on a au final une méthode complète pour mesurer la diversité : on représente le profil d’écoute des internautes sous la forme d’un graphe triparti, on effectue des marches aléatoires à partir des nœuds « internautes » vers les nœuds « catégories musicales » et on calcule l’indice de diversité de la distribution obtenue à partir de la formule précédente. En systématisant ce calcul à l’échelle de toute la plate-forme de streaming et de l’ensemble des internautes, on peut alors analyser à quel point les utilisateurs de cette plate-forme en ligne ont une écoute diversifiée.

Et les algorithmes dans tout ça ?

La démarche précédente nous permet ainsi d’analyser la diversité d’écoute des utilisateurs. Mais, en réalité, la méthode s’adapte à toute donnée qui s’exprime sous la forme de graphe triparti. Il est alors très facile d’étudier non pas le graphe décrivant quelles chansons ont été écoutées par les internautes mais quelles sont celles qui leur ont été recommandées, et donc d’analyser la diversité des algorithmes de recommandation eux-mêmes !

Et encore mieux, en comparant la diversité d’écoute des utilisateurs avant et après recommandation, il devient possible d’étudier l’effet des recommandations sur le comportement des utilisateurs et de contribuer ainsi au débat évoqué en introduction : est-il vrai que les algorithmes de recommandations s’adaptent au profil de diversité des internautes (des internautes diversifiés auraient des recommandations diversifiées) ? Les algorithmes de recommandations limitent-ils la sérendipité sur les plates-formes ou, au contraire, participent-ils à la découverte de nouvelles informations par les internautes ?

C’est ce que nous allons faire par la suite mais pour cela, essayons d’abord de comprendre comment on recommande du contenu à des internautes.

Le filtrage collaboratif

L’une des techniques les plus utilisées dans le domaine de la recommandation est très certainement le filtrage collaboratif, au cœur de nombreuses plates-formes basant leurs recommandations sur la personnalisation des contenus (Amazon, Netflix, Spotify…). L’idée de base est plutôt simple. Supposons que l’on désire faire une recommandation à un utilisateur. Plutôt que de tenter de recommander un contenu parmi ceux les plus en vogue du moment, on va tenter d’identifier quels sont les autres internautes qui ont un profil similaire, c’est-à-dire qui ont montré un intérêt pour les mêmes contenus par le passé. Dès lors, si ces individus au profil similaire ont aimé un contenu que l’utilisateur n’a pas encore visionné ou écouté, on va préférentiellement le lui proposer. On a donc sélectionné (filtrage) un contenu à partir d’autres internautes dont le comportement est proche (collaboratif).

Ainsi, dans l’illustration 2, on peut remarquer que Tao est l’internaute qui a le profil d’écoute le plus proche de celui d’Enzo. Ils ont tous les deux écouté Round Midnight et Castle in the hill par le passé. Un système de recommandation basé sur le filtrage collaboratif aura donc tendance à recommander à Enzo My Favorite Things, titre écouté par Tao mais qu’Enzo ne connaît pas encore. Inversement, Tao est aussi l’internaute ayant le profil d’écoute le plus proche de Bianca, à qui il sera suggéré d’écouter Castle in the hill.

Notons au passage que la recommandation basée sur Tao n’a pas du tout le même effet sur le profil de Bianca que sur celui d’Enzo. Dans le cas de Bianca, la recommandation l’incitant à écouter Castel in the hill a pour effet d’augmenter la diversité de son profil en lui faisant découvrir de nouveaux genres musicaux (le Pop et le Rock en l’occurrence). Dans le cas d’Enzo, l’effet est différent. Le fait de lui suggérer d’écouter My favorite Things va au contraire un peu plus déséquilibrer la distribution de probabilité issue d’une marche aléatoire partant de ce sommet utilisateur en renforçant un style musical déjà sur-représenté dans son profil d’écoute (le Jazz) au détriment des deux autres (Pop et Rock). Il en résulte que la diversité de son profil d’écoute après recommandation sera plus faible.

Les effets du filtrage collaboratif sur la diversité

Maintenant que tout le cadre théorique est en place, qu’en est-il concrètement ?

Un jeu de données public (Million Song Dataset) nous donne l’occasion de tester cette approche sur un cas réel, celui de l’écoute musicale en ligne. À partir de données liées à plus d’un million d’internautes ayant écouté environ 250 000 titres musicaux appartenant à plus de 1000 catégories, il a été possible de reconstruire un graphe triparti décrivant le profil d’écoute de ces internautes. Implémentant un algorithme classique basé sur le filtrage collaboratif, il a également été possible de proposer des recommandations personnalisées à chaque nœud internaute du graphe. Tout ceci nous permet d’analyser le comportement des internautes et des recommandations en termes de diversité.

Figure 1 : Diversité des recommandations en fonction de la diversité organique des utilisateurs (α=2). Source : Augustin Godinot & Fabien Tarissan.

La première question que l’on peut se poser est : est-ce que les recommandations suivent le profil de diversité des internautes. Autrement dit, est-ce qu’il y a une corrélation entre la diversité du profil de l’internaute et celle de ses recommandations personnalisées ? La figure 1 ci-dessus répond en partie à cette question. Cette figure compare la diversité « organique » des individus (c’est-à-dire celle correspondant au profil d’écoute) à celle des recommandations, chaque point désignant un nœud internaute différent avec son volume d’écoute (nombre de titres écoutés par le passé sur une échelle logarithmique en couleur). On voit très vite qu’il n’y a pas de lien fort entre les deux valeurs. Certains internautes ont une diversité très élevée (vers 50 et au delà) et les recommandations peinent à proposer des titres couvrant un tel éventail de catégories musicales quand d’autres internautes semblent avoir au contraire un univers musical assez restreint (diversité organique inférieure à 10) et les recommandations leur proposent de nouveaux horizons.

Ceci ne nous dit cependant rien encore de l’effet des recommandations sur la diversité d’écoute des internautes. Pour cela, comparons la diversité organique des individus à la diversité de ceux-ci s’ils suivent les recommandations qui leur sont proposées. Il s’agit ici d’une simulation dans laquelle l’ordre dans lequel les recommandations sont faites joue un rôle dans l’adhésion de l’internaute à cette recommandation (les recommandations faites en premier dans la liste ont un poids plus élevé). Le résultat est montré sur les figures suivantes (voir figure 2 ci-dessous), qui permettent également d’étudier l’effet du nombre de recommandations (10, 50 et 500, de gauche à droite) sur la diversité.

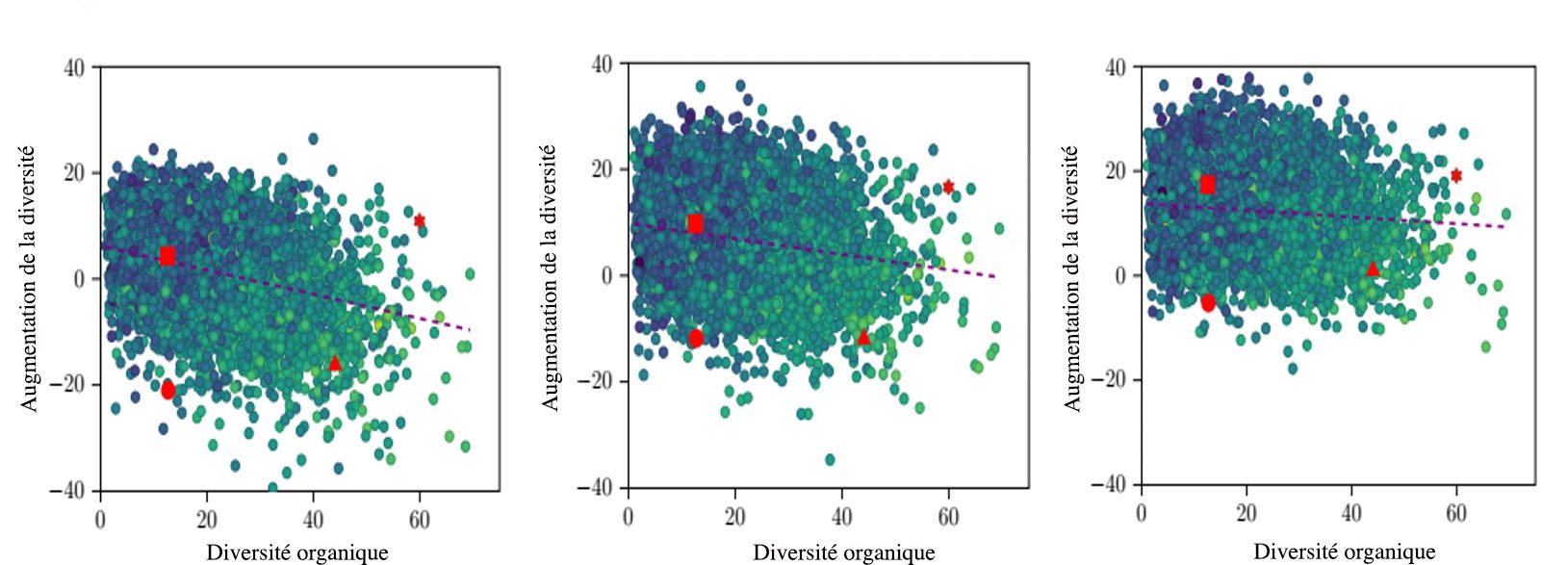
Figure 2 : Effet de 10 (gauche), 50 (milieu) et 500 (droite) recommandations sur les internautes en fonction de leur diversité organique (α=2). Source : Augustin Godinot & Fabien Tarissan.

L’effet des recommandations est alors plus clair : la capacité de l’algorithme de recommandation à accroître la diversité du profil d’écoute des internautes augmente avec le nombre de recommandations (les points sont de plus en plus haut).

Mais cet effet positif est relativisé par le fait que cet accroissement est particulièrement concentré sur les internautes qui ont un faible volume d’écoute (virant sur le bleu foncé) et/ou celles et ceux ayant un univers musical restreint (partie gauche des figures). Pour les autres, les recommandations peinent à maintenir un niveau égal de diversité, lorsqu’elles ne contribuent pas au contraire à une forme de confinement musical (accroissement négatif). Dès lors se pose alors la question de savoir comment prévoir l’effet des recommandations auxquelles sont exposés les internautes. Est-il possible de savoir, à partir d’un profil d’écoute donné, si les recommandations vont avoir tendance à favoriser ou, au contraire, restreindre, la diversité musicale de celles et ceux qui y sont exposés ? Sur ce point, il n’y a pas de réponse définitive mais l’étude individuelle de quelques cas particuliers suggère qu’il n’est pas du tout évident de prévoir l’effet des recommandations. 

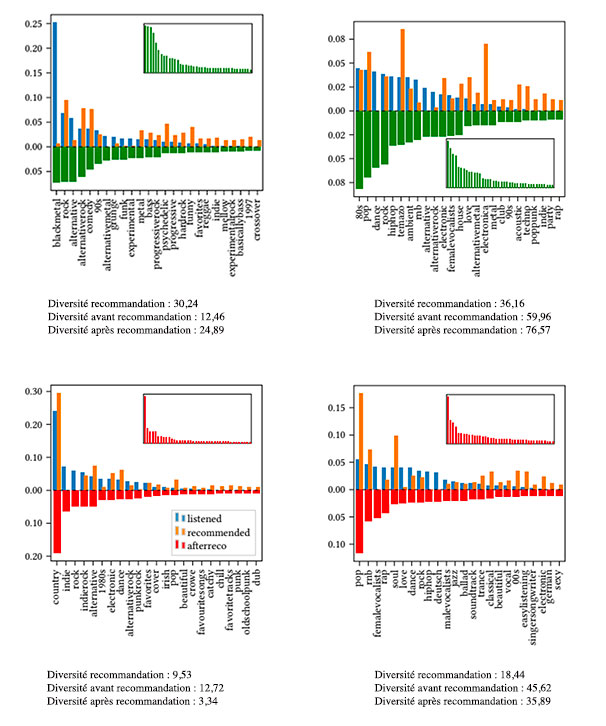
Figure 3 : Distribution du profil d’écoute pour quatre utilisateurs particuliers. Source  Augustin Godinot & Fabien Tarissan.

Ces figures montrent le cas de quatre individus dont le profil passé est faiblement (gauche) ou fortement (droite) diversifié et dont l’effet des recommandations est d’augmenter (haut) ou de diminuer (bas) la diversité des utilisateurs après exposition à 50 recommandations.

Chaque figure superpose plusieurs distributions de probabilité afin de comparer la diversité de l’internaute à différents moments : en bleu est montré le profil d’écoute « organique » de l’internaute (soit avant recommandation), en orange est représentée la distribution liée aux recommandations elles-mêmes, tandis que les distributions dirigées vers le bas montrent le profil d’écoute après recommandation, si l’internaute écoute les musiques suggérées (en rouge quand l’effet est négatif, en vert quand l’effet est positif). Pour ces trois moments, les valeurs précises de la diversité d’ordre 2 sont précisées sous les figures. Enfin, comme ces distributions sont tronquées pour permettre de voir les étiquettes des catégories les plus importantes pour chaque internaute, la distribution complète après recommandation est montrée dans un encadré à l’intérieur des figures (ici aussi en rouge ou en vert en fonction de l’effet négatif ou positif). Notons également que ces quatre individus se retrouvent dans la figure 2 puisqu’ils correspondent aux quatre symboles rouges présents dans différentes zones de la figure.

Ce que révèlent ces quatre cas d’étude est que des internautes aux profils similaires peuvent être affectés de manière très différente par les recommandations. Pour l’utilisateur en bas à gauche par exemple, la catégorie musicale la plus recommandée (country) correspond à la principale catégorie musicale écoutée par le passé, ce qui renforce le déséquilibre dans son univers musical et diminue donc mécaniquement la diversité (et ce, bien que la diversité des recommandations soit proche de celle de l’internaute !). Mais, de manière totalement inverse, l’utilisateur en haut à gauche, qui lui aussi a un univers musical particulièrement marqué, en l’occurrence le black metal, se voit exposé à des recommandations qui, au contraire, piochent très peu dans cette catégorie, choisissant plutôt d’autres univers musicaux connexes, écoutés ou non par cet internaute. Ceci a pour effet d’équilibrer un peu mieux les différentes catégories et donc d’augmenter la diversité.

Alors, que retenir de cette étude ?

Tout d’abord, et c’est le point principal, nous disposons d’une méthode objective pour quantifier la notion de diversité sur les plates-formes numériques, dès lors que celles-ci s’expriment sous forme de graphe, et cette méthode peut servir à la fois à analyser des traces laissées par les internautes dans leur utilisation des services en ligne, mais aussi à analyser les effets des systèmes de recommandations en termes de diversité.

Concernant les algorithmes de recommandation, l’analyse faite à partir d’une technique de recommandation particulière (le filtrage collaboratif) appliquée à un jeu de données particulier (contenant des profils d’écoutes musicales) a montré que les recommandations avaient plutôt tendance à améliorer la diversité des internautes (voir figure 1) et que cet effet augmente avec le nombre de recommandations (voir figure 2). Mais cette observation est nuancée par le fait que cet effet se concentre principalement sur les internautes écoutant peu de musique ou ayant un univers musical très restreint (figure 2). Pour les autres, les recommandations ont au contraire tendance à déséquilibrer le profil d’écoute et donc diminuer la diversité. Enfin, on a pu voir qu’à des profils d’écoute similaires peuvent correspondre des recommandations aux effets opposés (voir figure 3), ce qui souligne la difficulté à prévoir les effets des algorithmes de recommandation sur les internautes.

Tout ceci montre que, lorsqu’il est question de diversité, la manière dont les recommandations s’insèrent dans les habitudes d’écoute des internautes se révèle plus importante que la diversité des recommandations elles-mêmes.