L’intelligence en essaim ou comment faire complexe avec du simple ?
Mais dans la nature, on observe bien des formes d'intelligence. Pourquoi ne pas prendre en compte une intelligence qui ne serait plus individuelle, mais collective ? Les chercheurs ont ainsi conçu des systèmes « multi-agents » en s'inspirant du fonctionnement d'un groupe d'experts humains.
Une autre source d'inspiration est celle des sociétés d'insectes. Ainsi est née l'« intelligence en essaim », qui trouve des applications dans le domaine de la simulation et au-delà, par exemple en robotique collective ou pour les réseaux.
Un groupe d’experts humains qui doit résoudre un problème, ou encore une société d’insectes, peuvent devenir des sources d’inspiration pour concevoir un système informatique dont l’« intelligence » provient d’un ensemble d’entités – des « agents » – en interaction.
Dans le premier cas, lorsqu’on emploie la métaphore d’un collectif d’humains, chaque entité est supposée douée d’« intelligence ». Les agents communiquent directement en s’envoyant des messages, ils possèdent des représentations du problème à résoudre et sont capables de raisonnements élaborés. La complexité des modèles utilisés autorise à faire appel à des facultés cognitives avancées : représentation explicite et raisonnement sur les autres, raisonnement sur l’avancement de la résolution, persistance d’intentions, notion d’engagement, etc.

Formation d’un pont vivant chez la fourmi d’Argentine « Linepithema humile ».
Le comportement collectif de ces fourmis a servi de source d’inspiration au développement de techniques d’intelligence en essaim. Les informaticiens et les ingénieurs ont pu transformer des modèles du comportement collectif des insectes sociaux en méthodes utiles pour l’optimisation et le contrôle.
© CNRS Photothèque – Guy Théraulaz
Dans le second cas, au contraire, la métaphore est d’ordre biologique : les agents sont dotés de capacités restreintes de représentation et de raisonnement ; ils sont situés dans un environnement au travers duquel ils interagissent de manière indirecte en y déposant des marques. Alors que dans le premier cas, l’environnement est souvent absent, ici il joue un rôle primordial puisqu’il sert de support aux interactions entre les individus.
1. Une intelligence collective
On a longtemps cru (à tort) que les insectes sociaux étaient plus intelligents que les insectes solitaires, au vu des tâches complexes qu’ils accomplissaient. En effet, bien que ne pouvant être individuellement qualifiés d’intelligents, les membres de ces sociétés sont collectivement capables de réaliser des constructions sophistiquées, de s’adapter à des environnements changeants, de trouver le plus court chemin à une source de nourriture. Autant d’activités collectives dont la sophistication va bien au delà des simples capacités de chacun des individus : on parle alors d’intelligence collective.
Comment des termites, qui mesurent quelques centimètres, sont-elles capables de construire une termitière de plusieurs mètres de haut ?

Nid ou termitière de « Macrotermes bellicosus » dite : termitière cathédrale.
Savane de Côte d’Ivoire.
© CNRS Photothèque – Alain R. Devez
Est-ce en se concertant avec leurs congénères pour que toutes construisent les piliers à certains endroits ? On a longtemps pensé que la termite devait être capable individuellement de se représenter la termitière, de pouvoir se mettre d’accord avec ses congénères sur l’emplacement du pilier, etc. : c’est à dire que les capacités individuelles étaient du même ordre d’abstraction que la construction collective.
En fait c’est plus simple : aucune termite n’a idée de ce qu’est un pilier, ni ne communique explicitement avec ses congénères. Pour construire un pilier – ou du moins démarrer sa base – les règles suivantes suffisent :
a) construire une boulette de terre
b) poser aléatoirement la boulette avec une probabilité plus forte de la poser là où il y a déjà une autre boulette.
D’autres règles servent ensuite pour arrêter la construction.
L’intelligence en essaim
En Intelligence Artificielle, l’intelligence en essaim fait référence à cette intelligence collective des sociétés d’insectes. Elle a fait l’objet de nombreux travaux de recherche, voir par exemple ce mémoire téléchargeable en PDF.
L’intelligence en essaim consiste à étudier et à construire des sociétés d’individus artificiels simples qui sont capables collectivement de fournir une réponse complexe. Dans un tel système multiagent, chaque agent n’a qu’une vue limitée du système, mais il décide de manière autonome de ses actions. De ce fait, le système est caractérisé par un fonctionnement décentralisé : aucun agent ne décide ni ne coordonne les actions des autres.
Chaque agent est simple : il ne fait appel à aucune représentation ni mécanisme de raisonnement sophistiqué. Ainsi la résolution est le fait des interactions et de la dynamique du système : l’intelligence naît de façon collective. Le résultat global du système est donc émergent, constitué d’une succession de comportements de type « réflexes ».
Par exemple, imaginons un système multiagent dont l’objectif serait que chaque agent se dispose de manière équidistante sur un cercle de centre O et de rayon r. Cet objectif peut être atteint en dotant chaque agent de deux comportements élémentaires. Le premier comportement s’énonce ainsi : « se diriger jusqu’à une distance r du point O (perçu comme un stimulus de l’environnement) » et le second : « une fois à distance r de O, s’éloigner au maximum des autres ».
Cette applet a été développée avec NetLogo par Aurélien Saint-Dizier pour le site Interstices. Elle montre la capacité qu’ont des agents, placés aléatoirement au départ, à s’organiser seuls pour former un cercle, en se répartissant régulièrement autour de celui-ci.
Les agents, rouges à l’origine, deviendront jaunes quand ils seront dans une situation relativement stable, et verts dans une situation très stable. L’applet montre aussi l’importance du réglage des paramètres : en effet, des paramètres mal adaptés ne permettent pas d’arriver à une situation stable.
Quel est le principe ?
Les agents (points rouges à l’écran) n’ont que deux comportements très simples :
- S’éloigner ou se rapprocher d’un point de référence (le centre du cercle, le point blanc à l’écran) pour s’en maintenir à une certaine distance.
- Fuir ses voisins s’ils sont trop près.
Avec la première action, les agents vont se placer à une certaine distance du point de référence, sans se préoccuper de la position des autres agents. Du coup, tous les agents peuvent se retrouver au même endroit !
Avec la seconde action, les agents vont se repousser les uns des autres, s’ils sont trop proches. La répulsion sera alors d’autant plus forte que les agents sont rapprochés. Les agents vont donc chercher à maintenir une distance minimale avec leurs voisins.
La combinaison des deux actions va alors entrainer la formation du cercle.
Les agents vont commencer à se rapprocher du bord du cercle, et du coup, de leurs voisins. Ils vont vouloir s’en éloigner, ce qui va les repousser un peu plus loin que l’endroit qu’ils visaient. De proche en proche, les agents vont d’abord se rapprocher du bord du cercle, puis s’éloigner de leurs voisins, et ainsi de suite. Les agents vont ainsi avoir tendance à « glisser » le long du cercle pour pouvoir se placer à un endroit plus favorable :
- où ils ne seront plus gênés par leurs voisins,
- ou alors, où ils seront « coincés » entre deux voisins et ne pourront plus bouger.
Au final, les agents formeront un cercle, en ayant un minimum d’espace entre eux.
Comment agir sur le programme ?
Lorsque vous cliquez sur le bouton « action/pause », des agents (en rouge) vont apparaître à l’écran. Un point blanc au centre indique la position désirée du centre du cercle. Ce point peut être déplacé en cliquant sur la surface de la simulation (zone noire).
Le programme va alors tourner sans fin jusqu’à ce que l’on appuie à nouveau sur le bouton « action/pause »; ou que l’on appuie sur « validation », qui provoquera la réinitialisation de la position des agents, de leur nombre, et de la position du centre.
Il est aussi possible d’agir pendant la simulation sur différents aspects :
- On peut changer le centre du cercle à tout instant en cliquant dans la zone noire,
- On peut modifier la distance souhaitée entre ce centre et les agents, en déplaçant le curseur « rayon »,
- On peut choisir la distance pour laquelle les agents s’estiment trop près de leurs voisins, et vont donc chercher à s’en éloigner (curseur « distance-perception »),
- On peut déterminer avec quelle force les agents vont fuir leurs voisins, c’est à dire, à quelle vitesse ils vont partir dans la direction opposée (curseur « force-repulsion »),
- Enfin, on peut ajouter ou supprimer des agents à tout moment, en cliquant sur les deux boutons baptisés « ajouter agent » et « retirer agent ».
Points à noter
Tout d’abord, le monde des agents est sphérique. Comme sur notre planète, si l’on avance toujours tout droit, on revient sur nos pas. Pour les agents, il en va de même, s’il sortent par un bord de l’écran, ils réapparaitront de l’autre coté. En plaçant le centre du cercle suffisamment au bord de la zone de simulation, le cercle formé commencera sur un bord, et finira sur l’autre.
Les agents peuvent aussi s’enfuir très vite ! En effet, un agent en fuite peut se retrouver subitement très proche d’un autre agent en fuite. De ce fait, ils seront tellement proche que la force de répulsion (qui, rappelons-le, et d’autant plus élevée que les agents sont proches) va être très importante! On pourra alors voir des agents qui sembleront « sauter » loin d’un autre.
Quelques trucs à essayer
- Que se passe-t-il quand on met de nombreux agents sur un cercle très petit ?
- Que se passe-t-il quand on met une distance de répulsion élevée avec une force de répulsion élevée ?
- Comment jouer sur les curseurs de distance de répulsion et de force pour stabiliser le cercle sans que des agents sautent partout ?
- De même, comment obtenir un cercle régulier selon le rayon de cercle choisi ?
Il est possible de changer plusieurs paramètres à la fois. Toutefois, afin d’observer ce que l’on souhaite, il est souvent plus sage de regarder l’influence des paramètres un par un.
Vous pouvez commencer par choisir un rayon, pour lequel vous allez mener des expériences. Ensuite, vous pourrez essayer d’abord l’influence de la distance de répulsion, puis de la force, et enfin du nombre d’agents. Enfin, quand vous commencerez à deviner les comportements, essayez de prédire les paramètres qui donneront de bons résultats avec un nouveau nombre d’agents.
Aurélien Saint-Dizier
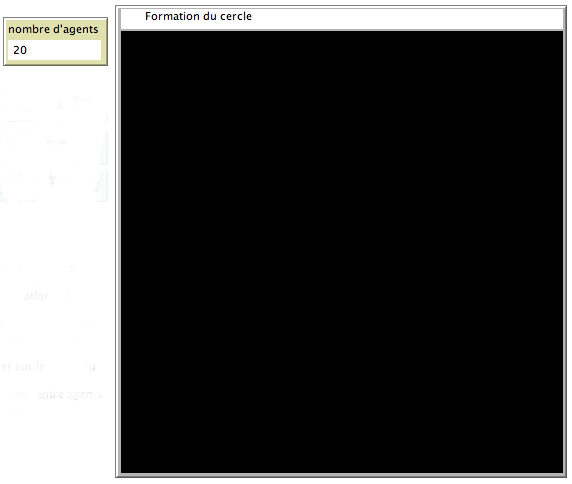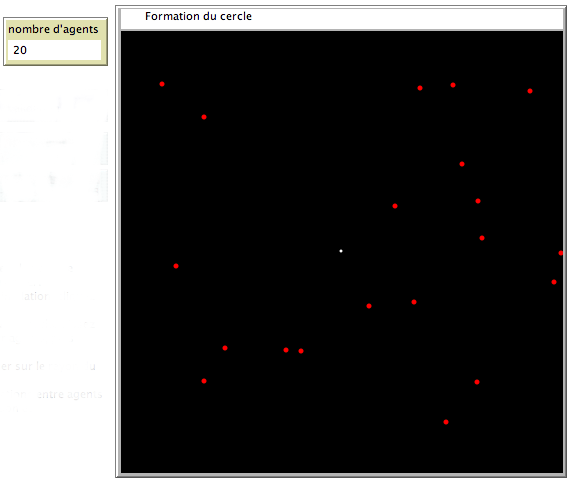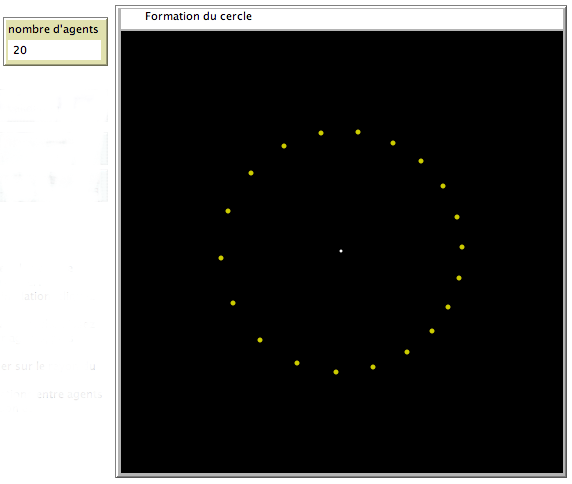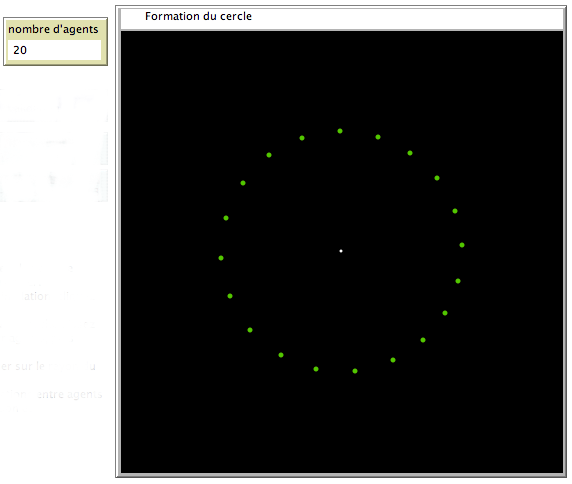
Un exemple de formation du cercle, en quelques étapes.
Avantage au collectif
De tels systèmes se caractérisent par leur adaptabilité et leur robustesse. En effet, du fait d’un contrôle décentralisé, chaque agent réagit en fonction de ses propres perceptions aux modifications de son contexte et il est capable de s’adapter continuellement aux variations de celui-ci. De plus, le nombre des agents, leur caractère interchangeable, l’absence d’entité centralisatrice rendent un tel système tolérant à la défaillance d’un de ses membres. Dans le cas de l’exemple du cercle, le nombre d’agents composant le système n’a pas besoin d’être précisé pour que le système fonctionne (on peut même ajouter ou supprimer des agents pendant qu’il fonctionne).
Ces deux propriétés permettent à un tel système de changer de comportement en cours de fonctionnement pour qu’il s’adapte aux évolutions de son environnement et d’avoir une dégradation progressive du fonctionnement collectif plutôt qu’un effondrement brutal.
Pour concevoir de tels systèmes, la difficulté principale qui se pose est de déterminer les comportements individuels, leur environnement et la dynamique qui va régir le fonctionnement du système afin qu’il produise la réponse collective souhaitée.
Cependant, les caractéristiques de ces modèles font qu’il est souvent difficile voire impossible de prédire a priori le comportement collectif à partir des comportements individuels. C’est pourquoi la mise au point de ces systèmes passe généralement par une phase expérimentale où l’on évalue le comportement global en fonction de différentes valeurs des paramètres du modèle.
2. …pour représenter et simuler des systèmes
Cette approche sert tout d’abord à représenter des comportements naturels observés, en biologie du comportement animal, en agronomie, en sociologie. Voici par exemple une simulation de la recherche de nourriture par les fourmis.
Elle se base sur la première expérience qui a permis de mettre en évidence l’intelligence collective développée par les fourmis en quête de nourriture. C’est cette expérience, menée dans les années 1980 par Jean-Louis Deneubourg, professeur à l’Université Libre de Bruxelles, qui est à l’origine du développement du domaine de recherche de l’intelligence en essaim.
Deux chemins de longueur différentes permettent aux fourmis d’accéder de leur nid à une source de nourriture. Une fourmi seule prendra indifféremment l’un ou l’autre chemin, alors qu’une colonie de fourmis choisira de manière privilégiée le chemin le plus court.
L’explication biologique de ce phénomène est assez simple. En effet, en se déplaçant, chaque fourmi marque son chemin en déposant une certaine quantité de phéromones. Au départ, les fourmis empruntent au hasard l’un des chemins. Mais celles qui ont pris le chemin le plus court retournent plus rapidement au nid, déposant donc plus rapidement une nouvelle quantité de phéromones sur le chemin du retour. Les autres fourmis sont ensuite guidées par les traces de phéromones les plus importantes. On observe donc qu’après un temps de convergence, le plus court chemin est emprunté collectivement par une majorité d’individus.
Cette applet a été développée avec NetLogo par Aurélien Saint-Dizier pour le site Interstices. Elle illustre la découverte du plus court chemin entre une fourmilière et une source de nourriture.
Des fourmis sortant à gauche vont essayer d’atteindre la nourriture à droite, en passant par l’un des deux chemins, puis chacune devra rentrer déposer la nourriture acquise. Après un certain nombre de passages des fourmis, l’une des branches deviendra très fréquentée : la plus courte entre la fourmilière et la nourriture.
Quel est le principe ?
Les fourmis, en bleu, sortent de la fourmilière. Elles ne savent pas par où passer pour trouver de la nourriture. Elles vont donc explorer le terrain à sa recherche. Afin de ne pas se perdre, les fourmis vont déposer des phéromones au fur et à mesure de leur exploration. Quand elles découvriront une source de nourriture, les fourmis vont ramener de la nourriture à la fourmilière. Elles vont pouvoir retrouver celle-ci en suivant la piste de phéromones qu’elles ont déposée en venant. (Les fourmis deviennent alors bleu clair.)
Afin que d’autres fourmis puissent trouver la source de nourriture convoitée, les fourmis sur le retour vont déposer une seconde phéromone (dite de ralliement) indiquant la présence de nourriture. A leur tour, les fourmis qui cherchaient de la nourriture vont suivre cette nouvelle piste, et accèderont plus rapidement à la source de nourriture.
Dans le cadre de cette simulation, les fourmis vont d’abord explorer aléatoirement les deux chemins, et les fourmis ayant emprunté le chemin le plus court seront les premières satisfaites. Elles emprunteront alors le chemin de l’aller en remontant la piste de phéromones leur permettant de rentrer, et déposeront une nouvelle piste de phéromones de ralliement.
Lorsque les fourmis sur le retour arriveront à proximité du nid, les fourmis sortantes vont être directement attirées par la piste de ralliement, et ne choisiront donc plus le chemin au hasard.
De ce fait, deux phénomènes vont se produire :
- une amplification de la piste des phéromones de retour, déposée par les fourmis en quête de nourriture,
- une amplification de la piste de ralliement vers la nourriture, déposée par les fourmis ramenant de la nourriture suivant la première piste.
Ceci fera qu’aux intersections, une piste sera plus concentrée que l’autre en phéromones dans les deux sens, et donc attirera un grand nombre de fourmis.
Comme la piste la plus courte donne généralement satisfaction en premier, elle sera donc rapidement la plus fréquentée.
Cependant, les phéromones s’évaporent avec le temps, ce qui permet de ne plus rallier les sources de nourriture vides.
Remarque : plus les fourmis s’éloignent de la source ou du nid, et moins elles déposent de phéromones. Ainsi, dans le cas de chemins complexes ou peu fréquentés, les fourmis peuvent suivre la piste dans le bon sens, en cherchant à aller vers l’endroit où il y a plus de phéromones.
Comment agir sur le programme ?
L’emploi de cette application est relativement simple.
- Pour commencer, il suffit de cliquer sur le bouton « action/pause », qui démarrera la simulation avec des paramètres par défaut. Pour le moment, il vous suffit de regarder et d’observer la découverte du plus court chemin.
- Pour interrompre la simulation, il suffit de cliquer de nouveau sur « action/pause » ; ou alors de cliquer sur « nouvelle simulation » pour en lancer une nouvelle.
- Les fourmis sortent de la fourmilière régulièrement au cours du temps, et partent en exploration. Grâce au curseur « nombre-fourmis », il est possible de changer à tout instant le nombre de fourmis souhaité dans la simulation. Si vous réduisez fortement le nombre de fourmis, celles qui sont en trop mourront alors. Au contraire, tant que le nombre de fourmis se promenant n’a pas atteint le nombre souhaité, de nouvelles sortiront de la fourmilière (Les fourmis sortantes sont bleues, les fourmis sur le retour sont bleu clair, et celles retournant à nouveau chercher de la nourriture sont bleu foncé).
- Un graphique permet de visualiser le pourcentage de fourmis sur chaque branche en fonction du temps. Vous pourrez y voir que même si la branche la plus longue est parfois plus fréquentée au tout début, c’est très rapidement la plus courte qui devient la piste favorite.
- Deux curseurs « évaporation-recherche » et « évaporation-retour » permettent de définir à quelle vitesse les phéromones s’évaporent une fois déposées.
« évaporation-recherche » correspond à la vitesse d’évaporation de la phéromone de ralliement, celle qui est suivie quand les fourmis sont en recherche de nourriture.
« évaporation-retour » correspond à la vitesse d’évaporation de la phéromone de retour à la fourmilière.
Le pourcentage indiqué par les curseurs donne le pourcentage de phéromones qui disparaîtra à chaque seconde.
Concernant l’affichage :
Il est tout d’abord possible de visualiser les traces chimiques des phéromones.
En cliquant sur « afficher-phéromones » un menu apparaît proposant :
- piste seule : n’affiche que la piste sous les fourmis,
- recherche : affiche un dégradé de couleur verte correspondant aux phéromones de ralliement,
- retour : affiche un dégradé de couleur rouge correspondant aux phéromones permettant le retour au nid.
Plus la couleur est claire, plus la quantité de phéromones est concentrée.
Enfin, le bouton « graphisme-fourmis » offre deux choix entre « point » et « fourmis ». Le mode « point » permet de symboliser les fourmis par de petits disques, plus simples à afficher, cela permet d’avoir une simulation plus rapide sur certains ordinateurs, surtout quand il y a beaucoup de fourmis à l’écran. Le mode « fourmis » quant à lui demande une machine plus puissante, pour que le programme ne ralentisse pas de trop.
Point à noter
La simulation a été faite pour aider les fourmis à trouver plus rapidement leur chemin (elle ne peuvent pas faire demi-tour pour changer de branche par exemple). Elles n’en ont pas besoin en pratique, mais ceci permet de constater plus rapidement le résultat, les simulations pouvant devenir beaucoup plus longues sans cette aide. Les fourmis ont donc pour indication : la nourriture est vers l’est par rapport à la fourmilière (mais elles ne savent pas où).
Quelques trucs à essayer
Vous pouvez jouer sur les curseurs d’évaporation pour observer à quel moment les fourmis ne peuvent plus retrouver facilement le plus court chemin. Voire même, quelles valeurs font que les fourmis, si elles ont commencé à visiter majoritairement la branche la plus longue, vont rester dessus, et « éviter » la plus courte.
Vous pourrez aussi jouer sur le nombre de fourmis et observer s’il y a un nombre minimum de fourmis nécessaire pour avoir une branche favorite.
Aurélien Saint-Dizier
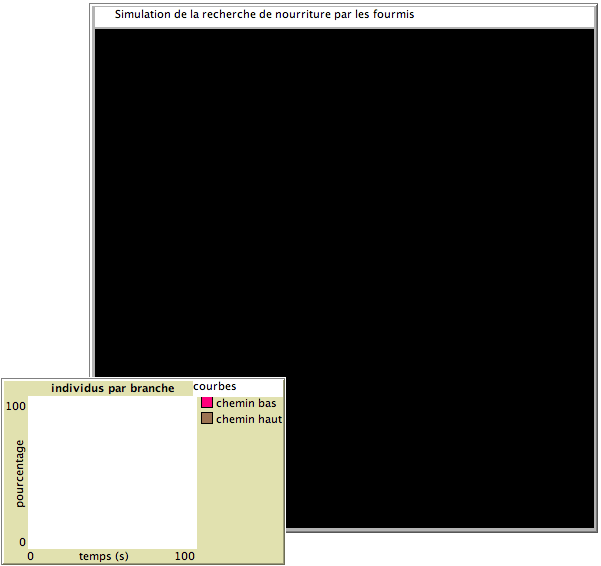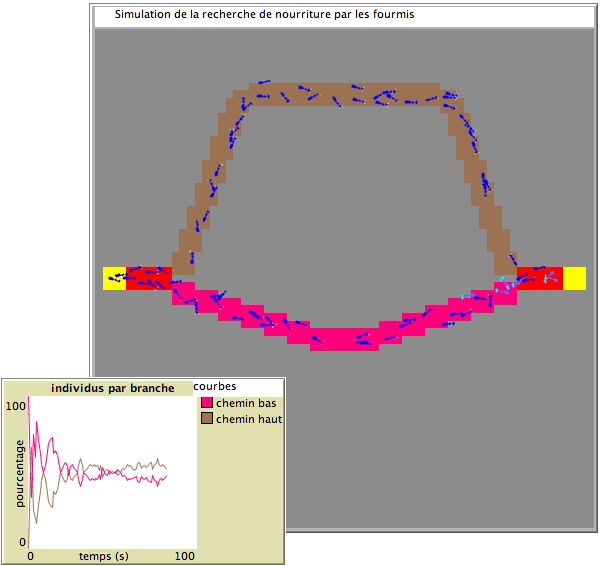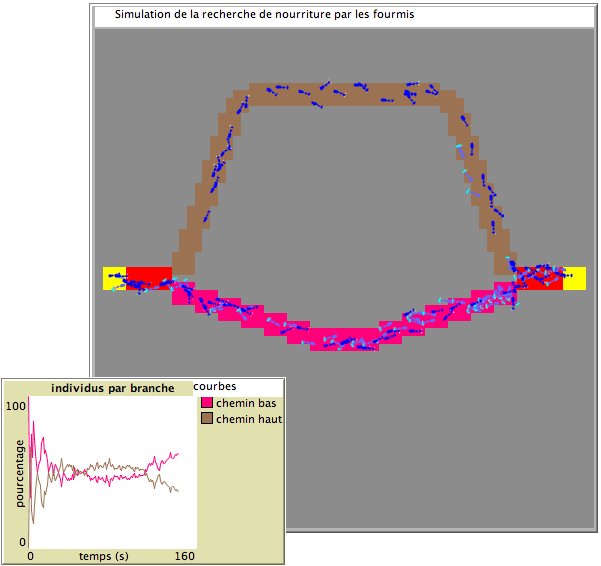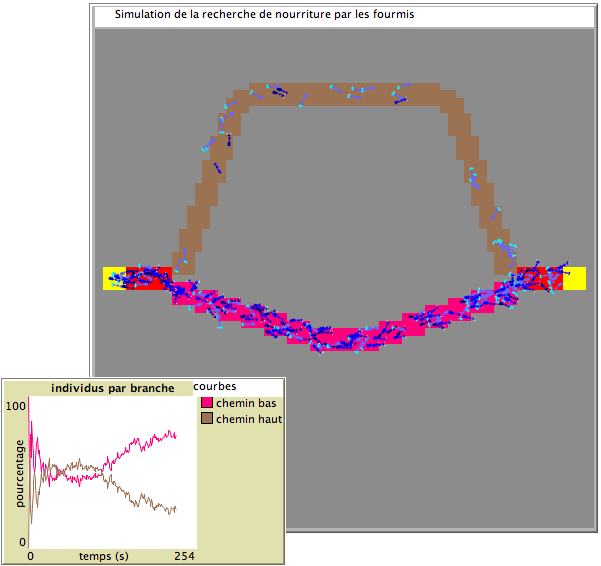
Un exemple de simulation de la recherche de nourriture par les fourmis, en quelques étapes.
Mais ce type d’approche ne se limite pas à la représentation de comportements naturels, l’intelligence en essaim est aussi appliquée à la gestion de trafics routiers urbains, à la simulation du mouvement de foule…
Ainsi, le logiciel MASSIVE (Multiple Agent Simulation System In Virtual Environnement) utilise ces principes pour créer des scènes d’animations de foules en 3D, dans le cadre du film « Le seigneur des anneaux ». Chaque agent d’une scène est défini par ses caractéristiques et ses réactions à son environnement. Les interactions entre centaines ou milliers d’agents produisent des mouvements de foule réalistes.
3. …pour résoudre des problèmes
Par ailleurs, cette approche peut être utilisée pour concevoir des systèmes de résolution collective de problèmes. Il s’agit alors de définir des comportements individuels en interaction pour que collectivement se produise une réponse qui sera interprétée comme solution d’un problème. Dans la construction de tels systèmes, les collectifs naturels servent de sources d’inspiration pour concevoir un algorithme de résolution collective de problème. Parmi tous les modèles qu’offre la biologie, les sociétés d’insectes figurent en bonne place.
L’un des tout premiers algorithmes s’inspirant du comportement d’une colonie de fourmis est dû à l’Italien Marco Dorigo, de l’Université Libre de Bruxelles. Cet algorithme, inspiré de la recherche de nourriture par les fourmis, s’applique au fameux problème du voyageur de commerce : quel est le chemin le plus court entre n villes qui passe une seule fois par chaque ville ?
Cet algorithme a servi de base pour mettre au point diverses applications, qui concernent par exemple les réseaux de communication, comme le routage d’informations dans un réseau. Les performances de ce type d’algorithmes sont comparables à celles d’approches plus conventionnelles.
Cette applet a été développée avec NetLogo par Aurélien Saint-Dizier pour le site Interstices.
Elle illustre la résolution du problème du voyageur de commerce. L’algorithme original ainsi que les paramètres expérimentaux qui ont été utilisés pour développer cette applet sont issus des travaux de Marco Dorigo, de l’Université Libre de Bruxelles.
Un voyageur doit passer par un certain nombre de villes, toutes différentes, et revenir à sa ville de départ. Il doit obligatoirement passer par chaque ville, et ne doit y aller qu’une seule fois durant son voyage. Le but est de trouver le chemin le plus court reliant toutes les villes.
L’applet montre que l’emploi d’un système de résolution basé sur le comportement des fourmis et leur capacité à trouver le plus court chemin entre deux points permet de résoudre un tel problème. Le programme donne le meilleur ordre des villes à visiter trouvé, ainsi que la longueur du trajet.
(Attention, selon la puissance de votre ordinateur, il faudra envisager d’être patient !)
Quel est le principe ?
Afin de trouver le parcours idéal, un ensemble de fourmis (autant que de villes) va être placé aléatoirement sur les différentes villes. À partir de ce point de départ, elles vont aller de ville en ville.
Les fourmis vont donc faire des tours (« cycles ») pendant lesquels elles vont se promener sur un chemin fermé reliant toutes les villes. On parlera de piste pour désigner la portion de chemin qui relie deux villes.
À chaque passage sur une piste entre deux villes, les fourmis vont déposer des phéromones ; la quantité déposée sera élevée si la piste est courte, et à l’inverse, faible, si la piste est longue.
De ce fait, pendant chaque cycle, les fourmis auront un choix à faire en arrivant dans une nouvelle ville : où aller ensuite?
Pour répondre à cette question, les fourmis vont être influencées par deux critères :
- suivre une piste ayant des phéromones,
- s’orienter vers une autre ville aléatoirement, en privilégiant les plus proches.
Cela signifie que les fourmis vont avoir une certaine probabilité d’aller dans la ville suivante. Cette probabilité sera plus élevée :
- si la piste a beaucoup de phéromones (donc est fréquentée),
- ou si la ville est proche.
À l’inverse, elle sera plus faible :
- si la piste est peu fréquentée,
- ou si la ville est loin.
Cependant, suivre une piste fréquentée augmente les risques de suivre toujours les mêmes pistes dans le même ordre et donc de suivre toujours le même chemin, en évitant des pistes aboutissant à des chemins potentiellement meilleurs. À l’opposé, suivre des pistes aléatoirement donne moins de chance de tomber sur la suite de villes idéale. C’est pourquoi les deux facteurs entrent en ligne de compte, et permettent ensemble de trouver le plus court chemin.
Afin que les phéromones ne s’accumulent pas d’un cycle à l’autre, incitant les fourmis à toujours prendre le même chemin, elles vont s’évaporer en partie entre deux cycles afin de permettre l’utilisation de nouvelles pistes.
Comment agir sur le programme ?
Pour lancer une simulation par défaut, cliquez sur « action/pause ». 20 villes vont être placées aléatoirement sur la carte.
Pour interrompre ou reprendre l’exécution du programme, cliquez sur « action/pause ».
Vous pouvez choisir le nombre de villes à placer sur la carte à l’aide du curseur « nombre-villes » et en cliquant ensuite sur « validation ».
Lors des simulations vous pouvez agir sur deux paramètres :
- « importance-aléatoire » qui détermine l’importance du critère aléatoire dans le choix de l’ordre des villes à visiter.
Quand cette valeur vaut 0, les fourmis ne suivent que les pistes ayant des phéromones, et suivront donc prioritairement les pistes les plus visitées.
Quand cette valeur vaut 6, les fourmis ne suivront pas du tout les pistes de phéromones, et choisiront les villes aléatoirement, en favorisant les villes les plus proches de leur ville courante. - « évaporation » détermine la quantité de phéromones qui va s’évaporer à chaque cycle, donc à chaque tour complet des fourmis. Plus l’évaporation est élevée, plus les pistes de phéromones vont s’effacer, et donc plus elles seront difficiles à suivre et attireront peu les fourmis. Plus elle sera faible, plus les pistes déjà fréquentées seront marquées et seront prisées lors du choix de la ville suivante.
Concernant l’affichage, il est possible d’afficher le chemin correspondant au meilleur choix trouvé, en choisissant « meilleur chemin » dans la liste « afficher ». Il est aussi possible d’afficher les phéromones en choisissant « phéromones »; les phéromones apparaîtront alors en nuances de vert, plus cette nuance est claire, plus il y a de phéromones sur ce passage.
Points à noter
Le monde des fourmis est ici entièrement plat. Les individus ne peuvent sortir par un bord de l’écran pour rejoindre l’autre bord, contrairement à la simulation du cercle.
Les facteurs d’évaporation et de choix aléatoire sont complémentaires. Bien que ceux-ci semblent avoir un effet similaire, il n’agissent pas sur les mêmes critères. L’aléatoire agit sur le choix de la ville suivante lorsqu’une fourmi cherche à faire un tour ; tandis que l’évaporation agit sur l’importance qu’a un chemin déjà exploré par rapport aux autres et donc incite les fourmis à chercher des pistes proches de ce chemin.
Il faut parfois être patient. Selon le nombre de villes, et la complexité de leur répartition, de nombreux cycles (de l’ordre de la centaine, parfois du millier) peuvent être nécessaires pour trouver la meilleure route. Il est même possible que le système ne trouve pas la meilleure route en un temps « raisonnable » pour l’utilisateur, mais une configuration très proche.
Des systèmes basés sur le même principe, mais plus avancés d’un point de vue technique donnent encore de meilleurs résultats ! Mais cela dépasse l’objectif d’illustration de ce programme.
À titre d’information, la méthode mise en place pour cette présentation, basée sur les travaux de Marco Dorigo, permet de trouver la meilleure solution pour un problème avec 30 villes différentes et avec un nombre de cycle inférieur à 3000. (Ce nombre ne représente pas la vitesse du programme, car il dépend entièrement de la machine qui fait les calculs et des conditions d’utilisation. Par exemple, la même méthode sans aucun affichage serait déjà beaucoup plus rapide.)
Quelques trucs à essayer
Essayez de favoriser le caractère aléatoire de la recherche avec peu de villes.
Vous obtiendrez sûrement d’assez bons résultats. Mais en est il autant avec beaucoup de villes?
Aurélien Saint-Dizier
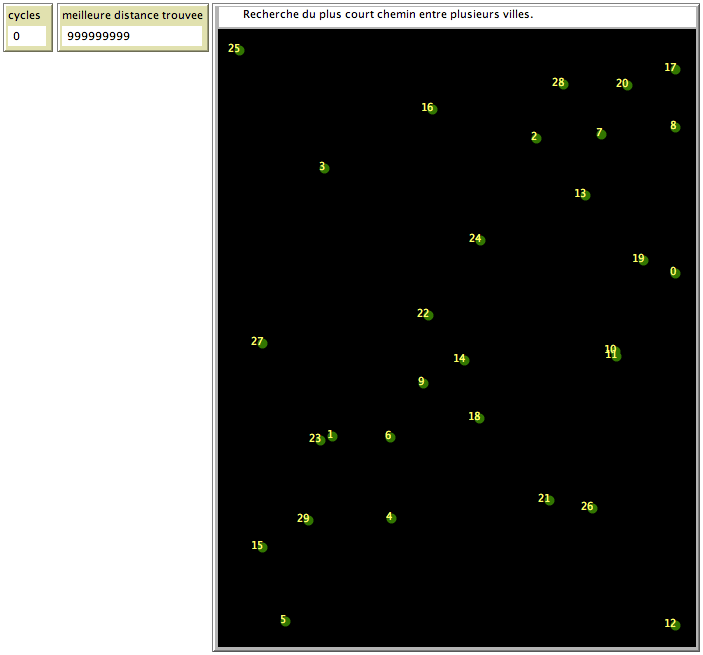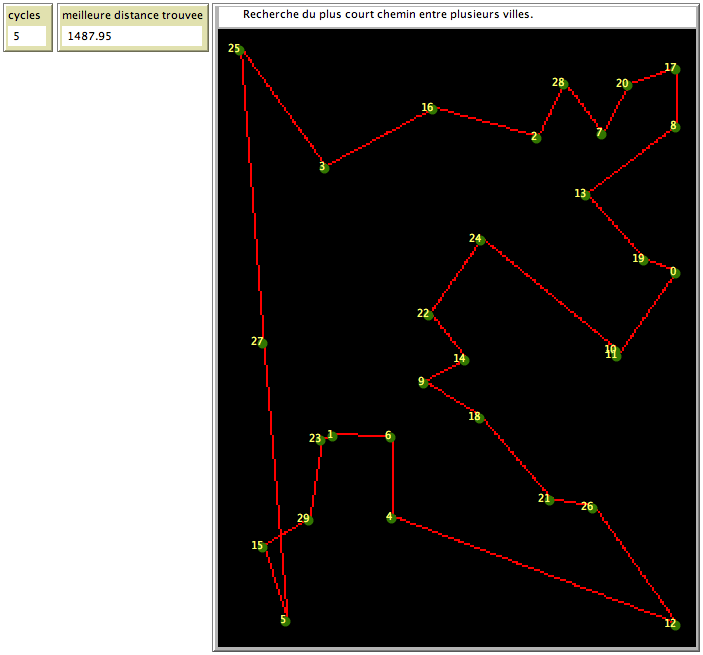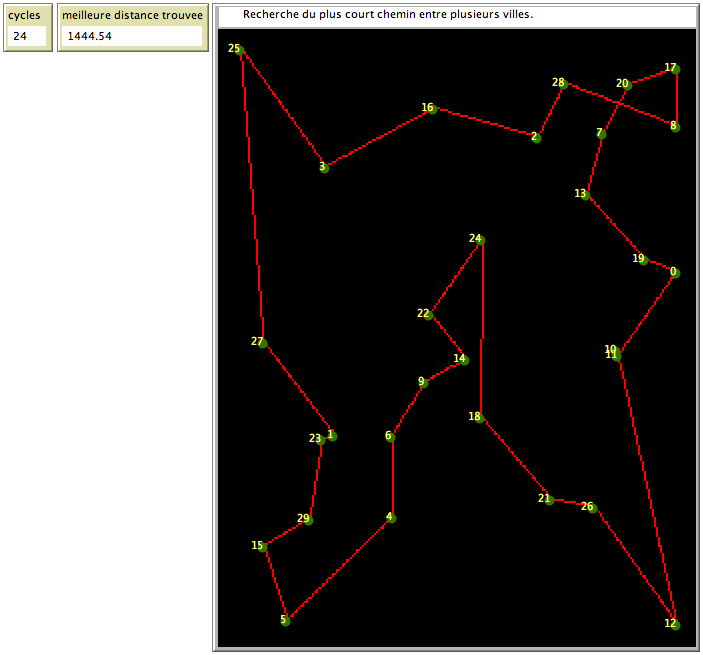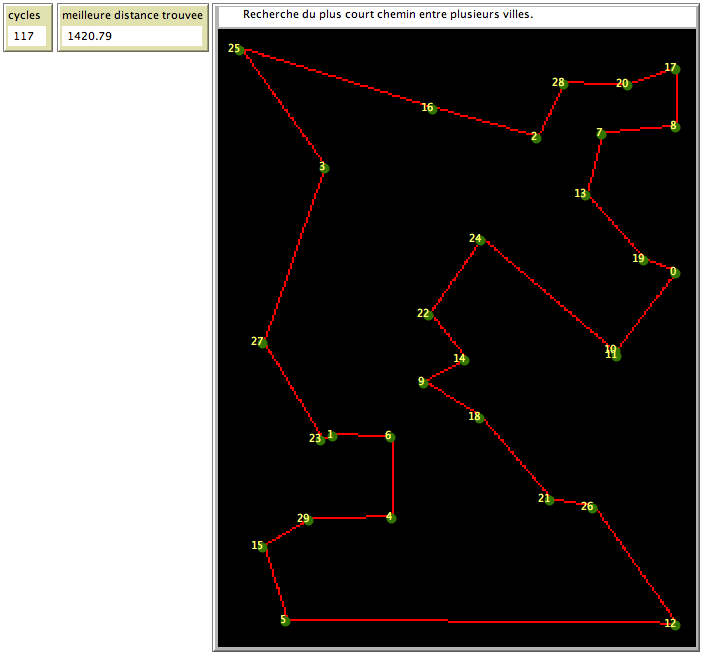
Un exemple de recherche du plus court chemin entre 30 villes, en quelques étapes.
Ces divers exemples montrent que l’approche d’intelligence en essaim est adaptée pour la modélisation de systèmes faisant intervenir un grand nombre d’entités différentes, en interaction, situées dans un environnement dynamique et fonctionnant de manière décentralisée.
C’est pourquoi elle s’applique bien à la simulation de phénomènes collectifs dont les propriétés globales ne découlent pas directement des propriétés de ses composants, en y apportant une dimension explicative.
Cependant, un grand nombre d’autres domaines de recherche actuels sont caractérisés par les éléments précédents (distribution, absence de point de vue global, environnement dynamique) et sont donc des champs potentiels d’application de cette approche, ne serait-ce qu’en robotique collective ou dans le domaine des réseaux (où la transposition du comportement collectif des fourmis a permis l’élaboration d’un algorithme efficace de routage).
Grâce aux évolutions technologiques, les systèmes informatiques sont de plus en plus omniprésents (on les retrouve dans les objets de la vie quotidienne), de plus en plus interconnectés, et toujours en fonctionnement. Cela préfigure donc des systèmes distribués, décentralisés, plongés dans un environnement dynamique et dont le fonctionnement global sera le résultat d’interactions entre les composants : un futur champ d’application pour l’intelligence en essaim ?
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Vincent Chevrier