Marchés financiers artificiels
Les marchés financiers fascinent par leur comportement imprévisible, voire exubérant, et les sommes colossales qui s’y échangent. Le moindre choc qui les secoue est porteur de conséquences sur l’économie entière, et potentiellement sur l’emploi et la consommation. Comprendre les mécanismes qui gouvernent leur dynamique est donc un enjeu scientifique majeur. Ce sera peut-être la clé de leur maîtrise. Les objectifs de la finance ? On peut en citer trois : décrire les dynamiques financières, les caractériser avec précision et les maîtriser à l’aide de méthodes et d’outils de gestion performants.
En cela, les années 1950 marquèrent la rupture avec les savoir-faire empiriques des praticiens au début du siècle précédent. La finance moderne se développa alors sous un angle scientifique rigoureux. Elle propose aujourd’hui un ensemble de modèles, mathématiques ou statistiques, dont l’usage s’est répandu bien au-delà des universités ; par exemple, la gestion de portefeuilles ou l’évaluation des options – des droits pour acheter ou vendre des actions – reposent sur une analyse précise des dynamiques boursières et sur des concepts d’optimisation. Grâce à ces avancées récentes, le couple risque-rentabilité est optimisé et on peut évaluer précisément le prix des produits dérivés, complexes ou exotiques.
|
|
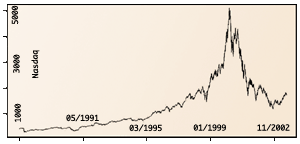
Les marchés artificiels reproduisent les places boursières réelles. Sur le New York Stock Exchange (à gauche), les opérateurs s’échangent des valeurs mondiales réelles. Leur comportement fit éclater une « bulle Internet » en 2000 : en quelques mois, le volume d’actions échangées fut divisé par deux (à droite).
Photo : skeeze via Pixabay, CC0 / Infographie : Pour la Science
Toutefois, certains rouages ou soubresauts des marchés financiers, pourtant très étudiés, nous échappent : nous n’avons pas su prévoir et éviter le krach d’octobre 1987, également connu sous le nom de lundi noir en référence au jeudi noir du krach de 1929, ni la bulle Internet à la fin des années 1990, ni prévenir certains scandales retentissants. Le premier d’entre eux est relatif au fonds d’investissement LTCM (Long Term Cash Management). Alors que deux futurs prix Nobel d’économie, Myron Scholes et Robert Merton, siégeaient à son conseil d’administration, la société a perdu des sommes abyssales en 1998, et faillit entraîner une grave instabilité du système financier mondial. Le second scandale est lié à la Barings, une des plus vieilles banques d’Angleterre. Celle-ci a participé au financement de l’achat de la Louisiane par les États-Unis à la France. Autre fait historique, c’était la banque de la famille royale britannique. En 1995, des spéculations hasardeuses faillirent provoquer la faillite de cette prestigieuse institution. Ne pouvant plus honorer ses engagements, contractés par l’opérateur Nick Leeson, la Barings fut rachetée par ING au prix symbolique d’une livre sterling. Leeson fit la une des journaux, et son histoire, contée dans un roman autobiographique intitulé Rogue Trader, fut mise en scène au cinéma en 2003 dans le film Trader.
Ces dernières années, la complexité du monde de la finance s’est accrue et pour y faire face, les analyses classiques, pourtant puissantes, sont insuffisantes. Aujourd’hui, on complète la description des phénomènes collectifs financiers par des approches théoriques centrées sur des individus et des interactions locales. La finance devient ainsi une discipline expérimentale ; parfois même, elle recourt à des expériences de laboratoire et à des simulations. Nous allons en présenter quelques-unes, en nous concentrant sur un sujet où elles sont particulièrement intéressantes : les bulles spéculatives.
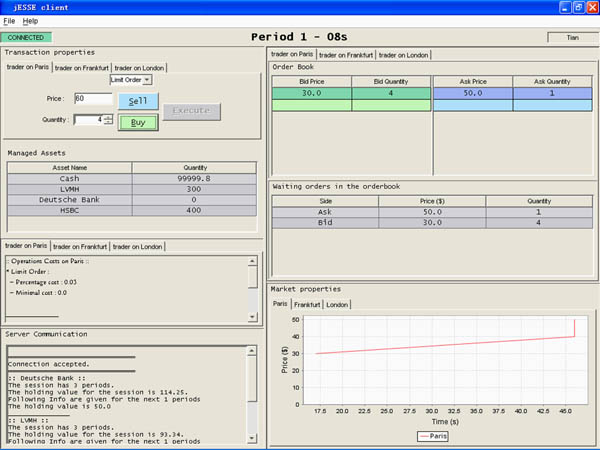
Source image : www.jessx.net
La finance moderne recourt à des expérimentations au cours desquelles les expérimentateurs (chercheurs, étudiants, etc.) peuvent se livrer à des simulations. Chacun dispose d’un ordinateur sur lequel il transmet des ordres (achat, vente, à tel prix, en telle quantité) à un ordinateur central, lequel assure la cotation (courbe en bas à droite). Cet outil est comparable à celui de places boursières informatisées, comme Paris.
Homo economicus et bulle spéculative
Avant le développement des techniques numériques sur ordinateur, la finance recourait à un autre type de simulation : les expériences de laboratoire. On doit cette idée provocante à Chamberlin, à la fin des années 1940 : à l’instar d’autres sciences, l’économie devenait alors une discipline expérimentale où on pouvait tester les théories dans des environnements contrôlés. Les toutes premières expériences de laboratoire en économie remontent au début des années 1930. Plus de 70 ans après, depuis l’obtention du prix Nobel d’économie par Vernon Smith en 2002, le recours à la simulation de laboratoire s’est généralisé.
Une grande part des théories économiques met en scène celui qu’on appelle l’Homo economicus. Cet être humain abstrait considère toutes les conséquences de ses choix, et ses décisions tendent à maximiser son bien-être. Rien ne l’affecte : ni influence sociale, ni psychologie, ni état d’âme. Ce modèle décrit les grandes lignes d’un comportement rationnel, à partir duquel toute la théorie financière s’est développée. Cet être abstrait nous ressemble-t-il ? À première vue, non. Nous ne sommes que de modestes Homo sapiens, éloignés de cette perfection. Cependant en théorie financière, on considère qu’un Homo economicus représente un individu « moyen ».
Pour vérifier le lien entre l’artefact et la réalité, intéressons-nous aux bulles spéculatives. On parle de bulle spéculative lorsque les prix observés sur un marché s’écartent de la « valeur fondamentale » des biens échangés. Imaginons que vous possédez un appartement et que vous le louez. Vous pouvez peut-être le valoriser en réalisant la délicate séquence d’opérations suivante : estimer l’ensemble des loyers que vous percevrez pendant plusieurs années, prendre en compte l’évolution du marché, les risques de non-paiement, les frais d’entretien, les impôts et les charges qui incombent au propriétaire, etc. Une fois votre calcul effectué, si vous constatez que le prix de vente de votre appartement sur le marché est supérieur à la valeur que vous avez calculée, et que cet état est généralisé à un grand nombre de biens comme le vôtre, vous êtes sans doute dans une bulle spéculative immobilière : les biens s’échangent au-delà de ce qu’on appelle « la valeur fondamentale », qui ici correspond grossièrement au calcul proposé. Il en va de même des actions : leur valeur fondamentale dépend des revenus attachés à chacune d’entre elles.
D’aucuns pensent qu’une telle bulle spéculative a affecté, à la fin des années 1990, les valeurs des secteurs liés à l’informatique et aux télécommunications. Son apogée aurait vraisemblablement eu lieu en mars 2000. Cependant, une controverse oppose théoriciens et expérimentateurs à propos de ce phénomène financier. En effet, aux yeux de certains théoriciens, les bulles spéculatives n’existent pas. Si les opérateurs financiers sont de bons Homo economicus et qu’aucun frein – des commissions de bourse ou la possibilité de trouver une contrepartie sur le marché – n’entrave leur action, alors les prix révèlent à tout moment l’ensemble de l’information disponible sur les actifs financiers. Les bulles spéculatives seraient ainsi corrigées à mesure qu’on les détecte. Néanmoins, la situation est tout autre sur un marché expérimental. L’expérience réalisée par Vernon Smith, Jerry Suchanek et Arlington Williams en 1988, est à ce titre instructive.
Dans cette expérience, des étudiants Homo sapiens échangent un titre financier pendant 15 périodes, de quelques minutes chacune. Cet échange a lieu à un prix fixé au bon vouloir de chacun. À la fin de chaque période, les titres donnent droit à un coupon dont la valeur est de un ECU (Experimental Currency Unit, ou monnaie expérimentale fictive). Au début de l’expérience, chaque titre vaut 15 ECUs, après une période d’échange 14 ECUs, etc., jusqu’à la dernière période où la valeur des titres est de un ECU. Autrement dit, la valeur fondamentale de chaque titre, égale à la somme des dividendes à obtenir dans le futur, décroît en escalier en se transformant en monnaie. Quand la cloche indiquant la clôture des échanges retentit pour la dernière fois, les actifs détachent leur dernier coupon.
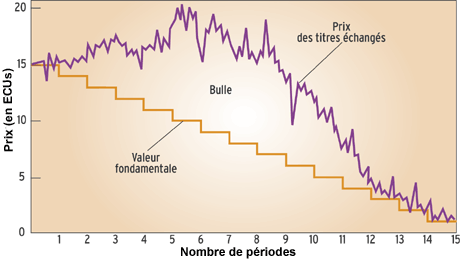
Lors de l’expérience de Vernon Smith, la vraie valeur des titres décroît au fil du temps, mais les étudiants s’échangent ces mêmes titres pour des montants supérieurs afin de réaliser des plus-values.
Infographie : Pour la Science
Avant que l’expérience ne commence, chaque participant reçoit un portefeuille, constitué de titres et de liquide, ainsi que les instructions lui donnant tous les éléments pour prendre de bonnes décisions. Pour éviter tout comportement excentrique des étudiants, V. Smith, J. Suchanek et A. Williams suscitent chez eux un comportement rationnel, au sens économique du terme : ils les rémunèrent en fonction de leurs gains relatifs obtenus à travers leurs échanges. Ceux-ci s’apprécient selon la variation de leur portefeuille initial : plus ils amassent de bénéfices, plus ils touchent une proportion importante de la somme allouée à l’expérience, en vrais dollars.
V. Smith, J. Suchanek et A.Williams s’attendaient à ce que les prix cotés par les étudiants soient voisins de la valeur fondamentale et que les volumes échangés soient faibles. Selon la théorie, même des Homo economicus attendraient passivement la fin de l’expérience pour encaisser les 15 ECUs ainsi que la rémunération correspondante. Eh bien non ! Les résultats s’avérèrent surprenants : non seulement les prix proposés par les étudiants s’écartaient durablement de la valeur fondamentale, mais le volume des transactions sur le marché était important. Une bulle spéculative apparaissait donc clairement. D’autres chercheurs ont réitéré cette expérience avec des étudiants ou des financiers professionnels, mais les résultats obtenus restent les mêmes. Les sujets expérimentaux ne cherchent pas à coller à la valeur vraie des titres. Au contraire, ils tentent de profiter de la tendance qu’ils ont eux-mêmes créée. Cette observation fait écho à John Maynard Keynes lorsqu’il affirme : « ils se préoccupent, non de la valeur véritable de l’investissement […], mais de la valeur que le marché, sous l’influence de la psychologie de masse, lui attribuera […] plus tard ».
Du laboratoire à l’informatique
Les expériences de laboratoire nécessitent un étroit contrôle de l’environnement des sujets expérimentaux et de leur motivation. Elles ne sont pas pour autant parfaitement reproductibles. Il est difficile de maîtriser la représentativité de l’échantillon, les raisons et les aversions qui ont poussé les sujets à prendre telle ou telle décision. Pour dépasser ces limites, on utilise un substitut de la réalité : la simulation informatique. Avec l’arrivée des premiers calculateurs électroniques, le terme de « simulation » a rapidement été associé à la résolution exacte ou approchée de systèmes d’équations décrivant des modèles économiques. Depuis, le sens s’est élargi, au point qu’une « simulation informatique » désigne désormais tout programme qui se substitue à une expérience.
Dans les années 1990, un nouveau genre de modélisation constituant un progrès significatif est apparu : la simulation informatique à base d’agents dotés d’intelligence artificielle. Avant de développer ce point et de montrer sa puissance de modélisation, nous allons voir quelles sont les limites des simulations et leurs applications pour la finance. Nous avons vu que la plupart des théoriciens assimilaient les acteurs économiques à des Homo economicus ; ils étudient donc un phénomène, à travers une représentation délibérément simplifiée. En outre, certaines de leurs analyses reposent sur une hypothèse forte quant au type de distribution des variations de cours, bien que les observations empiriques attestent que cette représentation est trop restrictive.
Bien sûr, la qualité des modèles, comme des simulations, s’apprécie à l’aune de leur conformité aux faits réels. Un bon modèle, une bonne simulation, doit rendre compte aussi précisément que possible de la réalité étudiée, ou tout au moins d’une partie de cette réalité. Cette condition n’est cependant pas suffisante. Par exemple, dans la physique d’Aristote, les objets « lourds » ont une tendance à rejoindre spontanément « leur lieu naturel », le bas. Ce « modèle » est bien confirmé par les faits… mais n’a plus grande pertinence dans le cadre de la physique newtonienne, qui fait intervenir, non pas une distinction entre corps lourd et léger, mais les notions de masse et d’attraction entre masses. Il convient donc de rester vigilant quant à la conformité des modèles aux faits, sans se laisser aveugler par ce seul critère. Inversement, des modèles capables de prédictions approximatives sont parfois préférés à d’autres plus précis. C’est le cas du modèle de Black et Scholes qui permet de calculer les prix des options à l’aide d’une équation semblable à l’équation de la diffusion de la chaleur. Sa marge d’erreur a longtemps été jugée tolérable au regard de sa simplicité.
Les simulations en sciences sociales sont vouées à deux grandes catégories d’applications. La première consiste à éprouver des théories ou des pratiques plus facilement qu’en situation réelle, comme l’effet d’une suspension de cotation en cas de fortes fluctuations dans le prix d’un titre financier. Un autre exemple est celui de la taxe Tobin. Suggérée en 1972 par le lauréat du prix Nobel James Tobin, cette taxation s’appliquerait sur les transactions financières et limiterait la spéculation ! Elle est difficilement testable en situation réelle. Le second champ d’utilisation est la reproduction sur ordinateur de situations artificielles. Celles-ci peuvent correspondre à des expériences de pensée. Par exemple, le modèle de ségrégation de Thomas Schelling indique comment émerge la ségrégation urbaine : il suffit que les agents d’une population hétérogène soient légèrement intolérants à la diversité dans leur voisinage pour que se forment des quartiers entiers peuplés d’individus semblables. Les situations artificielles peuvent aussi donner lieu à des interactions avec un acteur humain. Dans ce dernier cas, on se confronte à des situations plus ou moins réalistes, qui vont du simulateur pour l’enseignement à la mise en œuvre de plates-formes imitant parfaitement un marché financier. Un danger menace néanmoins le chercheur qui se repose sur une simulation : oublier qu’il ne travaille que sur un simple modèle du phénomène étudié, et non sur la réalité même. S’il observe une contradiction flagrante avec le phénomène réel, il doit réexaminer, voire rejeter le modèle.
Comme nous venons de le voir, la possibilité de simuler des situations économiques complexes ouvre de vastes perspectives. Jusqu’alors, la plupart des systèmes en finance, ou plus généralement en économie, considèrent des variables continues, et s’appuient sur des individus assez « homogènes » quant à leurs préférences, leurs anticipations ou leurs modes d’actions. À l’inverse, le monde économique est souvent discontinu et l’hypothèse d’homogénéité est discutable. Certains modèles mathématiques prennent en compte l’hétérogénéité des investisseurs en finance, mais ils deviennent rapidement insolvables ou nécessitent de multiples hypothèses simplificatrices. Par ailleurs, les phénomènes étudiés présentent une forte sensibilité aux paramètres et aux conditions initiales.
En outre, bien des modèles ne sont que descriptifs et ne se fondent pas sur une formalisation du comportement des investisseurs : c’est le cas de ceux qui prédisent les bouffées de volatilité, brusques changements de régimes dans les fluctuations des cours.
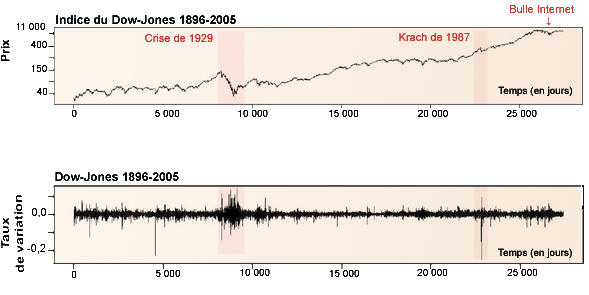
Les évolutions quotidiennes de l’indice Dow-Jones sur près de 100 ans sont représentées sur une échelle logarithmique (en haut), ainsi que ses variations quotidiennes (en bas). On peut voir des périodes de fortes fluctuations concentrées sur des intervalles de temps limités. Ces fluctuations intenses de prix, suivies de calmes relatifs, sont appelées des bouffées de volatilité. La plus importante est celle de la grande crise de 1929. Par comparaison, la bulle Internet est quasi invisible.
Infographie : Pour la Science
Grâce aux ordinateurs, on simule désormais le comportement de nombreux éléments hétérogènes en forte interaction. Cette possibilité ouvre la voie à des modélisations centrées sur des individus qui possèdent une histoire personnelle et une grande liberté de comportement : ce sont les modélisations multiagents (voir aussi La stratégie de l’araignée, par V. Chevrier et D. Chouchan). Depuis une quinzaine d’années, on a réexaminé avec ces nouvelles simulations des questions mal appréhendées jusqu’alors, notamment parce que les approches classiques devaient considérer des individus homogènes et ignorer les nombreuses rétroactions qui parcourent le système financier.
La modélisation des marchés financiers, comme leur simulation, recourt à des agents individualisés et hétérogènes.
- Un marché gouverné par une « loi de masse »
Dans ce type de modèle, l’hétérogénéité du monde est réduite à un « agent représentatif », ou « investisseur moyen » aux caractéristiques précises (l’Homo economicus). La dynamique des prix sur ce type de marchés, dans bien des modèles, est exprimée par des équations du type : Prix au temps t = prix au temps (t – 1) + aléa. Toute la difficulté réside dans la détermination de cet aléa et dans la spécification de sa dynamique propre.
- Un marché virtuel simplifié « synchrone »
Cette fois, le modèle, simulé sur ordinateur par des systèmes multiagents, tient compte de l’hétérogénéité des investisseurs. Ces derniers décident simultanément d’acheter ou de vendre en fonction d’un certain nombre d’informations : prix, historique des prix, etc.
L’équation dynamique est du type : Prix au temps t = prix au temps (t – 1) + un terme proportionnel à la différence entre la somme des achats au temps t et la somme des ventes au temps t. Tous les vendeurs et tous les acheteurs seront satisfaits à un prix qui découle de la balance de l’offre et de la demande. L’univers dans ce modèle est quasi continu (on peut échanger par exemple des fractions d’actions et les prix sont des nombres réels).
- Un marché artificiel « asynchrone » dirigé par les ordres

Dans ce type de simulations, les acheteurs et les vendeurs confrontent directement leurs enchères dans un carnet d’ordres. Celui-ci enregistre les propositions d’achat et de vente avec la limite de prix associée. La meilleure enchère « vendeur » (par exemple à 100) fait face à la meilleure enchère « acheteur » (par exemple à 95).
Si personne ne souhaite se porter contrepartie à ces prix, il se peut que le marché reste inactif et que nul ne soit servi. En revanche, il est toujours possible d’acheter immédiatement (ici à 100) ou de vendre (à 95), ou de formuler d’autres enchères plus avantageuses.
Ce type de marché artificiel implique une cotation en continu, un peu comme sur la bourse de Paris. L’univers dans ce modèle est donc discret (on ne peut échanger que des nombres entiers d’actions, et les prix ne s’expriment qu’en fonction d’un échelon de cotation, décimal le plus souvent). Le cours de l’action est cette fois-ci une conséquence des transactions effectuées à l’instant t. C’est la modélisation financière la plus fidèle à la philosophie multiagent.
Aux origines de ce courant de modélisation multiagent, Brian Arthur, un économiste à la pensée originale et controversée du Santa Fe Institute, aux États-Unis : il a marqué les esprits dans les années 1990 avec la question dite du Bar d’El Farol. Il s’agit là d’une de ces métaphores dont les chercheurs américains sont si friands !
Le bar d’El Farol

Le bar d’El Farol, selon une métaphore due à l’économiste Brian Arthur, est la sortie favorite de 100 habitants de Santa Fe. Cependant le plaisir d’y écouter de la musique est gâché lorsque la fréquentation excède 60 personnes. Quelle stratégie adopter, sachant que tout le monde prend sa décision au même moment et que les comportements sont déterministes ?
Photo © David Salazar / El Farol bar
De prime abord, le travail de B. Arthur n’a pas grand-chose à voir avec la finance : 100 personnes (des agents virtuels) se demandent toutes les semaines si oui ou non elles se rendront le jeudi suivant dans un bar de Santa Fe, le El Farol, où l’on donne des concerts de musique irlandaise. Hélas, le lieu est trop petit pour que tous puissent y tenir à leur aise : au-delà de 60 consommateurs (seuil critique de fréquentation ), le lieu devient intenable. Tous préfèrent aller au bar que rester chez eux, sauf si ce seuil critique est atteint. Cette dernière contrainte pousse les personnes à avoir des anticipations opposées : par exemple, si tous prévoient que le bar sera vide, tous décideront d’y aller ; le bar sera bondé, et personne ne sera satisfait.
Pour anticiper l’affluence au El Farol le jeudi suivant, aucun consommateur potentiel ne dispose d’un modèle théorique. En revanche, chacun possède des règles de décisions, plus ou moins élaborées, pour faire son choix. Ces règles consistent à « prédire le nombre probable de consommateurs jeudi prochain » et « en conséquence, aller ou non au bar ». Elles ne se basent que sur l’historique de la fréquentation au bar, il n’y a pas de stratégies aléatoires. Chaque agent virtuel utilise une règle, la meilleure, parmi l’ensemble de celles qui lui ont été attribuées. Le vendredi suivant (l’itération suivante), chacun examine s’il a bien fait ou non de se déplacer et reconsidère son ensemble de règles de décisions afin de déterminer celle qu’il utilisera la prochaine fois.
Les agents raisonnent de façon inductive, et leur rationalité est pour le moins limitée. Si l’on souhaite relier l’expérience de B. Arthur à la finance, on considère que les 60 places offertes correspondent à la quantité optimale de titres demandés à un prix donné. Toute demande supplémentaire de titre, au-delà de 60, entraîne un déséquilibre du rapport entre l’offre et la demande et donc une hausse des prix. Les agents obtiennent l’actif pour un prix supérieur à sa valeur fondamentale.
Avant d’aller plus loin, imaginons la fréquentation du El Farol sur un an ou deux, chaque jeudi : passe-t-elle alternativement à 100 puis 0 ? Oscille-t-elle uniformément entre ces bornes ? N’oublions pas qu’il n’y a pas de stratégie aléatoire ! B. Arthur constate que, aucun mécanisme élaboré n’intervenant, l’affluence moyenne au bar s’établit néanmoins à 60. D’après lui, ces agents limités dans leur rationalité, mais capables d’apprentissage, convergent collectivement vers le seuil critique de fréquentation. En ce qui concerne la finance, cela indique qu’une propriété jusqu’alors liée au modèle de l’Homo economicus, l’efficacité du marché financier, pourrait émerger de la forte interaction d’agents possédant une rationalité très limitée mais évolutive.
Le travail de B. Arthur a ainsi initié des modélisations multiagents, aujourd’hui en plein développement. La mise au point des premiers marchés financiers artificiels, comme le Santa Fe Artificial Stock Market, a nécessité des compétences interdisciplinaires. Créé en 1994, ce marché artificiel est le fruit de la collaboration des économistes Blake Le Baron et B. Arthur, du physicien Richard Palmer et des informaticiens John Holland et Paul Tayler. Il repose sur les mêmes bases que la simulation du problème d’El Farol, à savoir des investisseurs hétérogènes évoluant avec une rationalité limitée.
Avec ce type de simulation, on a mis en évidence des régimes de marché différents selon plusieurs paramètres, dont le nombre de règles de décision attribuées aux agents virtuels et leurs dotations financières initiales : les prix sont proches des valeurs fondamentales, ou très éloignés lors des épisodes de bulles spéculatives. Les résultats révèlent que de nombreux systèmes financiers artificiels évoluent au bord du chaos, sont sensibles aux conditions initiales et fortement influencés par les règles qui définissent la rationalité des agents.
La palette de modèles financiers multiagents est large. Les plus simples sont les toys models, où seuls quelques caractères jugés essentiels de la vie financière sont intégrés. Les simulations les plus abouties utilisent de nombreuses variables; elles « miment » la réalité avec une plus grande précision. Certaines équipes mettent au point des plates-formes où le comportement des agents est réglé par de véritables opérateurs qui mettent alors en scène leurs propres avatars. Plutôt que d’énumérer toutes les thématiques abordées par ces modélisations et simulations, nous allons poursuivre notre exploration des bulles spéculatives et évoquer ce que les financiers académiques appellent les faits stylisés, au travers du prisme particulier que nous offrent ces outils.
Une première explication des bulles spéculatives…
Un des avantages des simulations informatiques ? Elles permettent l’observation directe de la valeur fondamentale des titres échangés, alors que ce paramètre est inaccessible sur un marché réel. La caractérisation des bulles spéculatives est alors directe. Toutefois, les krachs boursiers recréés sont fondés sur des hypothèses toujours discutables : les relations entre la valeur fondamentale dans la réalité et les grandeurs macroéconomiques sont sources d’interrogation. Si on accepte cette limite, la simulation de modèles à agents hétérogènes nous renseigne sur le développement, la croissance et la mort violente de ces bulles.
Le comportement d’agents « irrationnels », mal informés ou manipulateurs, est-il à l’origine des bulles ? La population d’agents est-elle homogène, ou mêle-t-elle nécessairement différents types d’investisseurs aux stratégies opposées ? Nous n’avons pas le recul nécessaire pour répondre catégoriquement à ces questions. Cependant, certaines explications se dessinent : la formation des bulles spéculatives serait indépendante de l’irrationalité du comportement. En revanche, elle est vraisemblablement liée à la présence d’au moins deux comportements : celui d’agents « fondamentalistes », même en faible quantité, et celui d’agents « spéculatifs ». Les agents fondamentalistes cherchent constamment à profiter des décalages entre le prix de marché et leur appréciation de la valeur vraie des titres. La seconde catégorie d’agents sont des suiveurs de tendance. Désintéressés de la dynamique de la valeur fondamentale, ils sont par contre focalisés sur les mouvements d’ensemble du marché. Ces investisseurs « suiveurs de tendance » entraînent parfois les cours vers des sommets irréalistes, oubliant l’adage financier qui dit : « les arbres ne montent jamais au ciel ».
L’histoire nous montre bien que les marchés connaissent des renversements de tendance brutaux. Une baisse brutale du marché peut s’expliquer par la sensibilité du marché à la liquidité, c’est-à-dire à la possibilité pour un investisseur de vendre ses titres. Pour de nombreux théoriciens, notamment André Orléan, du Laboratoire Paris-Jourdan Sciences économiques, une des origines possibles aux paniques boursières est la peur qui saisit les spéculateurs lorsque la liquidité s’assèche. Elle les pousse à vendre de façon quasi synchrone, et par ce fait les spéculateurs accélèrent la raréfaction des contreparties possibles : le marché ne fonctionne plus si tout le monde fait la même chose ! En ajoutant ce comportement des investisseurs, on engendre des dynamiques financières qui ressemblent à certains épisodes de la vie financière passée.
… et des « faits stylisés »
Les marchés financiers renferment encore des phénomènes mal compris. Tel est le cas des « faits stylisés ». De quoi s’agit-il ?
De nombreux travaux empiriques de nature statistique se sont intéressés aux séries financières. On a dégagé des caractéristiques communes à ces séquences et on les a regroupées sous le nom de « faits stylisés ». Par exemple, les variations de cours sur un intervalle d’observation de l’ordre de la demie-heure ne sont pas corrélées, mais les valeurs absolues ou les carrés de ces variations le sont fréquemment. Elles sont concentrées par intervalles de variance très différente, les fameuses bouffées de volatilité, et ne sont pas distribuées selon une loi normale, loi représentée par une courbe en cloche qu’on appelle une gaussienne : on observe trop de rentabilités extrêmes pour satisfaire à ce critère.
Nous ne disposons pas véritablement d’explication qui décrive finement l’ensemble des mécanismes à l’origine de ces faits stylisés. Leur justification actuelle n’est pas fondée sur la définition d’un comportement spécifique des investisseurs. Nous savons les caractériser d’un point de vue statistique, mais pas encore les expliquer. Une telle explication devrait aussi prendre en compte l’organisation fine des marchés, ainsi que la nature des informations qui agite les places financières. De nombreuses équipes travaillent actuellement à la mise au point de modèles multi-agents parcimonieux, minimalistes, qui engendreraient une large variété de ces faits et en amélioreraient la compréhension. Pourquoi faire compliqué quand on peut faire simple ?
Ainsi les modélisations multi-agents rendent compte d’un univers complexe, hétérogène, dont bien des secrets résistent depuis plus d’un siècle malgré un effort de recherche constant. La perspective offerte par des simulations massives, où plusieurs millions d’agents économiques virtuels en interaction peuplent une économie virtuelle complète, s’avère prometteuse : la macroéconomie multi-agents naissante réinsérera peut-être les marchés financiers artificiels dans de vastes structures économiques où l’imbrication des organisations, des marchés, des règles et des individus sera mieux prise en compte.
En francais
- D. Goyeau et A. Tarazi, La Bourse, Éditions La Découverte, 2006
- André Orléan, Le pouvoir de la finance, Éditions Odile Jacob, 1999; voir aussi la vidéoconférence de l’Université de tous les savoirs sur le même sujet.
- Jean-Philippe Bouchaud, Les caprices des marchés financiers, une vidéoconférence de l’Université de tous les savoirs réalisée en 2000.
En anglais
- O. Brandouy et P. Mathieu, Large-scale agent-based simulations and the efficient markets hypothesis, Lecture Notes in economics and Mathematical Systems, C. Bruun (ed.), Springer Verlag, 2006
- Finance expérimentale : JessX, Java Experimental Simulated Stock Exchange
- Un exemple de simulation de marchés financiers à base d’agents sous la plate-forme NetLogo (environnement de programmation pour la modélisation / simulation des phénomènes collectifs naturels) : El Farol Bar problem.
Une première version de cet article est parue dans le dossier n°52 La modélisation informatique, exploration du réel de la revue Pour la Science, numéro de juillet/septembre 2006.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Olivier Brandouy

Philippe Mathieu
Professeur d'informatique, responsable de l'équipe Systèmes multi-agents et comportements (SMAC) du Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).