
Mieux gérer les ressources naturelles

Un banc d’albacores et quelques coryphènes pris au piège dans une senne au large des Seychelles (Océan Indien – 2006). © Ifremer-IRD/Fadio/M. Taquet.
La pression sur les ressources naturelles a commencé à s’accentuer dès le début de la révolution industrielle. À partir du XXe siècle, les avancées technologiques ont permis de créer de nouveaux produits, comme les ordinateurs ou les tablettes, très consommateurs de matières premières ayant une empreinte environnementale forte, tels le lithium ou les terres rares. Aujourd’hui, nous avons non seulement besoin d’une plus grande quantité, mais aussi d’une plus grande diversité de ressources. Cet impératif, essentiel pour le développement des pays les moins avancés autant que pour la croissance des grandes puissances, génère des tensions entre pays, comme à l’intérieur même des États.
Pour répondre aux besoins énergétiques, le premier réflexe a été de rechercher de nouvelles sources d’énergie, de nouvelles mines, de nouveaux territoires. En témoigne le choix de l’énergie nucléaire en France dans la deuxième moitié du XXe siècle. Mais l’existence d’une solution unique et globale est devenue de plus en plus improbable. On s’oriente donc vers une large adaptation des technologies, une utilisation plus rationnelle des multiples sources d’énergie (mix énergétique) et une exploitation plus raisonnée des ressources dans un souci de durabilité. Aujourd’hui, l’innovation ne réside plus dans la quête d’une solution unique, mais intègre de plus en plus une gestion durable des ressources naturelles. C’est typiquement l’idée des réseaux électriques intelligents, appelés smart grids, destinés à optimiser simultanément la production, la consommation et le stockage de l’énergie à l’échelle du réseau dans son intégralité.
Pour la gestion des milieux naturels, on s’oriente dans la même voie, vers une coexistence des usages qui permette d’utiliser dans la durée les multiples ressources disponibles. Par exemple, pour les milieux souterrains, il s’agit de faire cohabiter stockage d’énergie, ressource en eau et séquestration du dioxyde de carbone. Le stockage souterrain d’énergie peut s’effectuer sous forme thermique, en injectant de l’eau chaude en été et en la récupérant, toujours chaude, en hiver. Il pourrait être réalisé à grande échelle dans des couches géologiques suffisamment isolées des aquifères qui contiennent les réserves d’eau douce. Plus profondément, là où l’eau est naturellement salée et sans intérêt économique, on pourrait stocker le dioxyde de carbone et ainsi réduire notre impact sur le climat. La compartimentation verticale et latérale du milieu souterrain peut permettre la coexistence des différents usages.
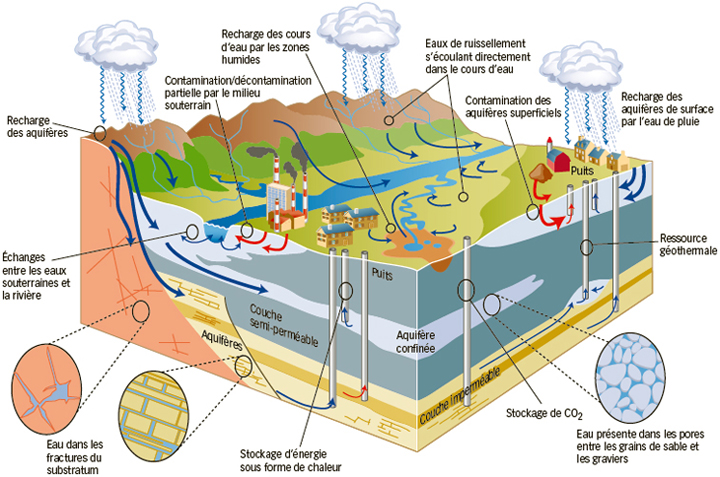
Vers une mixité des usages.
Réserve d’eau douce, stockage d’énergie, ressource géothermale et séquestration géologique du CO2 seront amenés à cohabiter.
© Vincent Landrin (d’après Natural Resources Canada).
Des apparences trompeuses
Ce concept de compartimentation est en fait très général et également pertinent pour la gestion de populations vivantes comme les ressources halieutiques. Pour éviter leur épuisement, il est nécessaire de laisser le temps à une partie des poissons de grandir et de se reproduire. Tout l’enjeu est de savoir quel est l’état de la population aux différentes périodes de l’année. Supposons que seule une partie des individus adultes puisse se reproduire, comme c’est le cas pour certaines espèces hermaphrodites de mérous. Intuitivement, on est enclin à penser qu’il faut suivre les effectifs des poissons adultes fertiles et que la proportion des poissons adultes stériles est sans réel intérêt. Le traitement mathématique rigoureux de ce problème prouve qu’au contraire c’est le comptage des poissons adultes stériles qui donne accès à la dynamique globale de la population. Cet exemple indique la nécessité de réaliser une analyse mathématique complète du problème et montre qu’un raisonnement trop simpliste peut être préjudiciable à la connaissance et donc à l’exploitation des ressources.
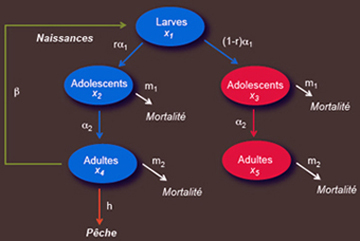
© Alain Rapaport/INRA.
Considérons une population de poissons ayant plusieurs stades de croissance : larvaire, adolescent et adulte. On suppose que cette population possède les caractéristiques suivantes. Seule une proportion r du taux de larves qui évoluent vers des adolescents donnera des individus capables de se reproduire lorsqu’ils seront adultes. Les adultes non féconds sont reconnaissables par un trait physique (ils sont par exemple de plus petite taille). Les stades adolescent et adulte sont soumis à un taux de mortalité naturelle, notés respectivement m1 et m2. Seuls les adultes féconds sont pêchés pour être commercialisés, et sont capturés avec un taux h (les adultes non féconds sont rejetés à la mer, car ils n’ont pas d’intérêt économique). La reproduction n’est pas synchronisée : à tout instant, un taux α1 de larves devient adolescent et un taux α2 d’adolescents devient adulte. Les adultes féconds se reproduisent avec un taux noté β. On peut représenter l’état de la population par le schéma d’interdépendances ci-dessus.
Si la pression de pêche sur les adultes féconds est trop importante, les naissances diminueront et on risque à terme un épuisement de la population. C’est ce que l’on appelle la surexploitation de la ressource halieutique. Il faut donc trouver un compromis pour satisfaire le marché économique sur le court terme et préserver la ressource sur le long terme, en ajustant au cours du temps la variable de décision h (par exemple en imposant un quota à certaines époques). Pour ce faire, on a besoin de prédire l’évolution des densités des cinq sous-populations.
On peut traduire le schéma d’interdépendances en un modèle mathématique qui représente l’évolution temporelle des densités (ou effectifs) de ces cinq sous-populations, notées xi (i = 1,…,5), en fonction des différents taux m1, m2, α1, α2 et β, de la proportion r et du terme de pêche h, à l’aide d’un système d’équations différentielles linéaires. Idéalement, il faudrait connaître à tout instant les cinq variables xi, l’intégration du modèle mathématique permettant alors de prédire l’évolution dans le temps de la population en fonction de la politique de pêche choisie. Le plus souvent, il est difficile voire impossible de mesurer ces densités, notamment celles des stades larvaire et adolescent, ponctuellement affectés par des événements externes non maîtrisés, donc non pris en compte dans ce modèle (prédations, pollutions, incidents climatiques, etc.). Néanmoins, le relevé des captures donne en général une estimation de la densité de la population exploitée, ici la variable x4 des adultes féconds.
Dans le vocabulaire de la théorie des systèmes, on appelle variable de « sortie », notée y(t), une variable mesurée, ici la densité des adultes féconds : y(t) = x4(t). Le problème dit d’« observation » consiste à examiner s’il est possible de reconstruire l’état complet x(t) du système à l’instant t à partir des seules mesures du passé de la variable de sortie : {y(τ), τ ∈ [0,t[}. La réponse est donnée par le calcul matriciel (en supposant les paramètres r, α1, α2, β, m1 et m2 connus). L’analyse montre que l’observation de la densité des adultes féconds (c’est-à-dire l’ensemble des mesures passées jusqu’à l’instant t), notée y(.), n’apporte pas une information suffisante pour reconstruire les autres densités. Si, à la place ou en plus, on estime la densité des adultes non féconds (en comptant les individus capturés dans les filets avant de les rejeter à la mer), ce qui revient à prendre comme variable de sortie y(t) = x5(t) ou bien y(t) = x4(t) + x5(t), alors le système est dit « observable » et on peut théoriquement estimer les densités des autres sous-populations à l’aide d’un « capteur logiciel ».
Les deux cas précédents mettent en évidence qu’on ne peut se limiter à considérer seulement la ressource, sans prendre en compte ses relations avec les compartiments ou avec les familles voisines. Un autre exemple très éloquent est fourni par l’exploitation des réserves en eau souterraine. Selon le bon sens, il ne faudrait pas pomper plus d’eau que la quantité qui s’infiltre dans la nappe, appelée recharge. C’est un raisonnement incomplet qui néglige à tort deux processus clefs. La recharge peut augmenter avec la quantité d’eau pompée : lorsque la nappe est pleine, prélever davantage d’eau stimule sa recharge. En revanche, quand le niveau de la nappe est bas, le pompage est susceptible d’avoir des effets néfastes sur la vie dans les cours d’eau, qui sont, en été, essentiellement alimentés par les nappes phréatiques. Une étude simple du bilan hydrologique montre l’interdépendance entre les réserves hydriques des cours d’eau et des nappes et souligne la nécessité de leur gestion conjointe.
Les différentes ressources sont susceptibles d’interagir les unes avec les autres. Pour se prémunir contre ces interactions, on peut séparer géographiquement l’utilisation de chacune d’elles : une zone pour la biodiversité, une pour la ressource en eau, une pour l’exploitation d’un gisement de matières premières, etc. En revanche, si on ne souhaite pas se limiter à une sanctuarisation du milieu naturel et à une segmentation stricte, il faut développer une connaissance et une maîtrise plus importante des divers compartiments et ressources les uns vis-à-vis des autres. L’intuition et le bon sens ne suffisent alors plus. Et c’est là qu’interviennent les modèles et l’analyse mathématique, à la charnière entre observations et gestion.
De multiples difficultés à surmonter
De nombreux modèles mathématiques permettent déjà de représenter et d’appréhender des systèmes complexes, mais le contexte des milieux naturels introduit quelques spécificités particulièrement contraignantes. On a vu l’importance cruciale de la dimension spatiale, de la compartimentation et des interfaces entre les compartiments. Les domaines considérés sont également très grands. Par exemple, une nappe phréatique peut s’étendre sur des centaines de kilomètres et recouvrir une grande variété de conditions géologiques. La dimension temporelle est aussi critique. La réponse des systèmes n’est parfois perceptible qu’après un temps très long : une pollution accidentelle qui percole dans le sol peut mettre plusieurs années pour atteindre un puits de pompage ; la fiabilité d’un site de stockage géologique s’évalue en dizaines, voire en centaines d’années pour le dioxyde de carbone et en millénaires pour les déchets nucléaires… Enfin, les ressources biologiques vivantes évoluent constamment face aux modifications de leur environnement. L’organisation spatiale, l’évolution temporelle et la complexité des interactions posent de grands défis à la méthodologie scientifique.
Premièrement, il est impossible de faire des expériences grandeur nature et en temps réel pour vérifier les modèles. C’est pourtant la démarche scientifique classique sur laquelle repose la fiabilité de nos systèmes industriels. Il faut donc développer un grand degré de confiance dans les modèles pour accepter leurs prédictions sans avoir la capacité de réaliser une expérience pour les tester. Une analyse mathématique poussée permet néanmoins d’avoir des indications de convergence du modèle vers la réalité. Cela souligne également l’intérêt des modèles simples comme des modèles complexes. Les modèles complexes sont plus proches de la réalité, mais sont parfois difficilement interprétables. Les modèles simples (comme celui évoqué en encart) apportent une compréhension complémentaire.
Deuxièmement, les modèles ne sont pas des représentations un pour un de la réalité car on ne peut pas décomposer le milieu naturel en un nombre limité de parties observables. Un modèle n’est pas une maquette, comme celles d’une voiture ou d’un avion, mais une représentation partielle du réel. Il est similaire à la réalité, il est cohérent avec le maximum d’observations disponibles, mais sa proximité vis-à-vis de la réalité reste inconnue. Que plusieurs modèles soient équivalents pour l’une de leurs propriétés n’entraîne pas qu’ils le soient pour une autre. Pourtant, ce n’est pas parce que les modèles sont imparfaits qu’ils ne sont pas utiles. Plutôt que de parler de maquette, on parlera d’analogue en définissant plus précisément le contenu de l’analogie. Cette notion d’analogue est notamment utilisée dans l’industrie pétrolière pour optimiser les stratégies d’exploitation. Les analogues sont régulièrement modifiés, améliorés en fonction des chroniques de production, ce qui demande à la fois une grande capacité d’interaction avec les opérateurs et une plasticité certaine pour adapter les modèles aux observations et à l’intuition des exploitants.
Probabilité versus sécurité
Les modèles ne fournissent pas une prévision, mais plutôt une prédiction, un ensemble de scénarios de référence. Ce qui signifie que l’on est capable de produire des tendances générales avec une certaine probabilité, mais pas des prévisions fixes qui se réalisent presque sûrement — exactement comme dans les prédictions d’évolution climatique pour les prochaines décennies. Toute une gamme de modèles respectent les mêmes contraintes, sont cohérents avec les mêmes observations, mais donnent des prédictions variées. Dans ce contexte, la gestion est d’autant plus délicate car le manque de vérification, l’absence d’un contrôle complet pose des questions majeures. On pense par exemple à l’exploitation des gaz de schiste ou au stockage des déchets nucléaires. Sur quel scénario doit-être prise la décision : sur celui qui est le plus défavorable mais aussi le moins probable ? sur une moyenne plus probable mais impliquant davantage de risques ? Pour les gaz de schiste, la variété des situations aux États-Unis, au Canada et en France illustre bien que la décision n’est pas seulement une affaire de connaissances, mais est aussi fonction de la culture, de la législation et de la confiance que chaque société accorde aux études scientifiques. Dans ce contexte, la rigueur et la transparence de l’analyse mathématique sont des atouts déterminants pour rechercher les solutions le plus adaptées aux problèmes complexes posés.
- D’andréa-Novel Brigitte, Cohen de Lara Michel. Cours d’automatique : commande linéaire des systèmes dynamiques. Paris : Presses des Mines, 2000.
- Bacaër Nicolas. Histoires de mathématiques et de populations. Paris : Cassini, 2009.
Cet article est paru dans la revue Textes et documents pour la classe (TDC) n° 1062 « Les mathématiques de la Terre », éditée par le CNDP, en partenariat avec Inria et à l’initiative du comité éditorial d’Interstices.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Alain Rapaport