Modéliser les interactions au fil du temps

Tout au long de la journée, vous entrez en contact avec de nombreuses personnes. Imaginez que toutes ces interactions soient enregistrées. Le matin, vous emmenez votre fils à l’école à pied. En route, vous rencontrez un de ses amis et sa maman, et finissez le chemin ensemble. Arrivés à l’école, les enfants retrouvent leurs copains. Quant à vous, vous retrouvez certains parents avec lesquels vous sympathisez, et décidez d’aller prendre un café. Une fois votre café pris, vous allez au bureau où vous retrouvez vos collègues. Vous filez à une réunion, après laquelle vous avez rendez-vous avec un collègue pour lui expliquer un projet. Pendant ce temps, les enfants sont en classe, puis sortent en récréation et jouent en petits groupes. De temps en temps, un enfant change de groupe…

Habituellement, les interactions comme celles-ci sont étudiées sous forme de réseaux, ou graphes. Les individus sont représentés par des nœuds et un lien est présent entre deux nœuds si les deux individus correspondants ont été en contact. Autrement dit, on considère des ensembles de paires (x, y) indiquant que les individus x et y ont interagi. La figure ci-dessous montre un petit exemple.

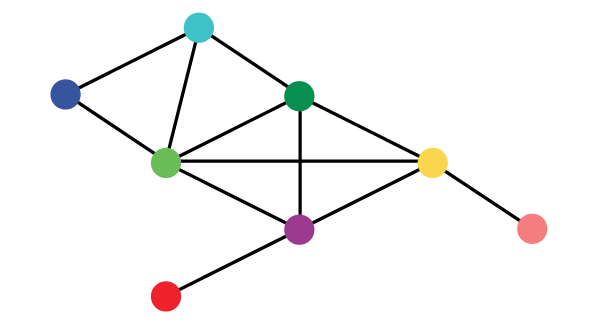
Un réseau d’interactions entre des individus. Par exemple, l’individu vert foncé est en relation avec le vert clair, le bleu clair, le violet et le jaune, alors que l’individu rouge n’interagit qu’avec le violet. Les individus vert clair, vert foncé, violet et jaune sont tous en relation les uns avec les autres. Il en va de même pour les individus bleu clair, bleu foncé et vert clair.

Dans une société, certains groupes d’individus sont densément reliés : il y a beaucoup d’interactions entre eux. C’est par exemple le cas des membres d’une famille, de groupes d’amis ou de collègues. On peut évaluer ceci par la densité d’un groupe dans un réseau : il s’agit de la probabilité, quand on choisit deux individus du groupe au hasard, qu’il y ait un lien entre eux. Autrement dit, la densité indique à quel point tous les membres du groupe interagissent entre eux : si elle est égale à 0 alors il n’y a aucune interaction, et plus elle se rapproche de 1 plus on est dans une situation où tout le monde interagit avec tout le monde dans le groupe. Ainsi, dans l’exemple ci-dessus, la densité entre les enfants est plus grande qu’entre enfants et adultes : les enfants interagissent plus entre eux qu’avec les adultes. De même, la densité entre adultes est élevée, et elle l’est également entre les membres d’une même famille.

Formellement, pour un ensemble de n nœuds entre lesquels m liens sont présents, la densité δ est égale au nombre de liens m divisé par le nombre maximal de liens possibles entre n nœuds soit n . (n-1) / 2. On a donc δ = 2 . m / (n . (n-1))

Parfois, les individus d’un groupe interagissent carrément avec tous les autres membres du groupe. Lorsqu’on prend deux individus au hasard, on est sûr qu’ils interagissent, la densité du groupe est alors égale à 1. Un tel groupe est appelé une clique dans le réseau. En voyez-vous dans la figure ci-dessus ? Elle contient en particulier une clique de 4 individus. Les cliques sont étudiées par les scientifiques depuis longtemps, car elles sont révélatrices de groupes particuliers et ont des propriétés algorithmiques extrêmement fortes.

Ces notions de réseaux, de densité et de cliques ont donné lieu à de nombreux résultats mathématiques et à des applications variées, aussi bien en bioinformatique que dans les télécommunications. Toutefois, elles ignorent un point essentiel : la dynamique des interactions, c’est-à-dire le fait qu’elles ont lieu à des moments spécifiques dans le temps. Difficile dans ces conditions d’obtenir un éclairage sur la régularité des relations, sur les événements inhabituels, sur la diffusion de maladies ou de rumeurs entre individus… Beaucoup d’information est ainsi perdue, quel dommage !

Pourquoi étudier la dynamique des interactions

De très nombreuses situations peuvent se modéliser comme des interactions au cours du temps : des appels téléphoniques, du trafic réseau, des échanges de messages, des achats en ligne, des flux financiers, des contacts physiques, même l’activité cérébrale, et bien d’autres… Mieux comprendre la structure et la dynamique de ces interactions a donc de nombreuses applications : la détection d’attaques menées par plusieurs machines sur l’internet, la lutte contre les fraudes à la carte bancaire ou le blanchiment d’argent, la distribution de contenus comme des actualités sur les téléphones mobiles, l’optimisation des services et produits proposés aux usagers, la détection de signes avant-coureurs de crises d’épilepsie…

Par exemple, dans des forums de discussion entre personnes sur l’internet, la densité des interactions révèle des événements comme des controverses ou des scissions. On peut détecter et gérer au mieux de tels événements directement en étudiant la structure et la dynamique des échanges, sans avoir besoin d’en analyser le contenu, c’est-à-dire le texte des messages. Ceci permet de préserver la confidentialité des échanges, ce qui n’est pas crucial sur un forum public mais prend une tout autre dimension si les échanges ne sont pas publics, par téléphone par exemple, ou par messagerie personnelle.

Autre exemple, les séries d’interactions denses dans du trafic réseau sur l’internet peuvent révéler des ensembles de machines se coordonnant, potentiellement pour en attaquer une autre. Prévenir de telles attaques est crucial, et être capable d’analyser finement des séries d’interactions temporelles ouvre de nouvelles perspectives très prometteuses dans cette direction.

Comment étudier la dynamique des interactions

Depuis quelques années, dans ce qu’on appelle la science des réseaux, beaucoup d’efforts sont consacrés à l’étude de la dynamique des réseaux. Beaucoup d’idées intéressantes ont été proposées, mais la plupart reviennent d’une façon ou d’une autre à couper le temps en tranches : on regarde qui a interagi avec qui pendant une première période de temps, puis qui a interagi avec qui pendant la seconde période, puis pendant la suivante, et ainsi de suite. On obtient ainsi une série de réseaux, dont on peut étudier les propriétés au fil du temps.

Pour l’ensemble de contacts de notre exemple initial, on étudiera par exemple le réseau des individus interagissant de 7 heures à 8 heures, de 8 heures à 9 heures, de 9 heures à 10 heures, etc. On obtiendra alors un réseau pour chaque tranche d’une heure, sans distinction de la chronologie des rencontres à l’intérieur de chaque tranche horaire. L’étude de la dynamique des interactions sera ramenée à l’étude de cette série de réseaux. On regardera par exemple l’évolution de leur densité, ou encore si certains groupes denses à un moment donné restent denses au cours du temps.

Dans cette approche où l’on discrétise le temps de manière uniforme, un problème bien identifié est celui de la granularité de la discrétisation. Pour plus de précision, faudrait-il considérer des tranches d’un quart d’heure, ou d’une minute ? Et pourquoi pas des tranches de taille variable ? Dans cet exemple on pourrait distinguer le temps du trajet, de 8 h à 8 h 30, puis le temps de classe, de 8 h 30 à 11h30, la pause de midi, de 11 h 30 à 13 h 30, etc.

Plus grave, une fois les interactions représentées par une série de réseaux, on ne sait pas vraiment comment étudier cette série. Par exemple, on peut regarder comment évolue la densité du réseau au cours du temps, mais comment pourrait-on définir une densité des interactions au cours du temps ?

Pour répondre à cette problématique, une nouvelle approche est actuellement développée. Plutôt que de transformer les interactions en séries de réseaux qu’on espère étudier grâce aux outils de la science des réseaux, il s’agit de développer directement une science des interactions. L’objet considéré est alors un ensemble de triplets (t, x, y) indiquant le fait que les individus x et y ont interagi à l’instant t, comme représenté sur la figure ci-dessous. De cette façon, on n’a plus à transformer les données, à se débarrasser du temps en le découpant en tranches : on intègre le temps directement à la description des interactions.

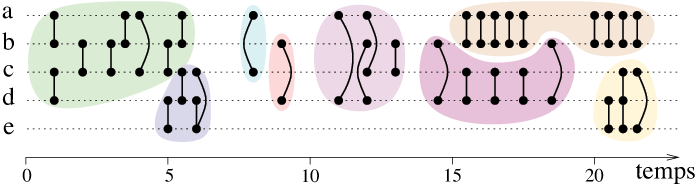
Une série d’interactions entre cinq individus. Les individus sont notés a, b, c, d et e. Le temps est découpé en instants numérotés à partir de 0. Chaque lien représente une interaction à un certain instant. Par exemple, à l’instant 5, b et c sont en interaction, ainsi que d et e. Chaque zone colorée indique un sous-ensemble d’interactions particulièrement denses. Cette densité est temporelle, les interactions sont nombreuses entre deux instants proches. Elle est aussi structurelle, les individus impliqués interagissent presque tous entre eux.

La question posée est alors de définir une notion de densité qui convienne à cette nouvelle représentation, afin de mesurer non seulement à quel point tout le monde interagit avec tout le monde mais également à quel point cela se produit tout le temps. On obtient alors une notion simple à énoncer : la densité des interactions est la probabilité, quand on prend deux individus au hasard et un instant au hasard, que ces deux individus interagissent à cet instant-là.

Formellement, on considère un ensemble de n nœuds dont on observe les interactions pendant une durée dont le nombre total d’instants est noté τ. On note T(x, y) le nombre d’instants où a été observée une interaction entre x et y. La densité δ se calcule avec la formule suivante, où x et y parcourent l’ensemble des nœuds :

\[\delta = \frac{2\cdot \sum_{x,y} T(x,y)}{n\cdot(n-1)\cdot {\tau}}\]

Une fois cette notion de densité définie, une foule d’autres notions en découlent. En particulier, une clique dans une série d’interactions est tout simplement un ensemble d’individus et un intervalle de temps tels que tous ces individus interagissent en permanence pendant cet intervalle de temps : leurs interactions ont une densité égale à 1. Ainsi, dans l’exemple des contacts sur le chemin de l’école, la densité entre vous et votre fils est égale à 1 pendant la durée du trajet : vous interagissez en permanence et donc formez une clique. Vous formez également une clique avec les parents d’élèves qui vous accompagnent prendre un café, pendant la durée de cette pause. Et ainsi de suite.

Cette nouvelle approche, qui préfère définir une science des séries d’interactions plutôt que de transformer les séries d’interactions en réseaux plus ou moins dynamiques, est en plein développement. Elle permet d’intégrer de façon cohérente la nature à la fois structurelle et temporelle des interactions : qui interagit avec qui, et quand.