
Pierre, feuille, ciseaux…
« Les mathématiciens sont comme les Français : quoi que vous leur disiez, ils le traduisent dans leur propre langue et le transforment en quelque chose de totalement différent. »
(Goethe)
Et de très intéressant… aurait dû ajouter Goethe : ainsi les mathématiciens ont transformé un jeu d’enfants Pierre-feuille-ciseaux en un riche modèle des interactions animales.

L’Américaine Andrea Farina, vainqueur du championnat du monde en 2007.
© RPS Championship
Qui n’a joué à ce jeu ? La pierre (P) casse les ciseaux, les ciseaux (C) découpent la feuille et la feuille (F) enveloppe la pierre. Deux joueurs, placent chacun leur main droite dans le dos, et choisissent l’un des trois symboles : le poing fermé pour la pierre, la main allongée pour la feuille, deux doigts en forme de ciseaux. Les deux joueurs dévoilent leur choix en avançant la main, parfois en proférant un cri. Si les deux choix sont identiques, ils recommencent, sinon le joueur qui détient le symbole le plus fort des deux a gagné le coup.
Le jeu est ancien et l’on en trouve des traces en Chine dès l’époque Ming (1368-1644). Il est connu dans le monde entier et ses variantes sont innombrables. On y joue avec un plus grand nombre de symboles, on ajoute le puits, le feu, l’eau, etc., ou alors avec d’autres triplets. Dans une version japonaise, les trois symboles sont le guerrier, le tigre et la mère du guerrier. Il y a aussi le feu, le serpent et l’eau, et encore le serpent, la grenouille et la limace.
Pierre-feuille-ciseaux est pratiqué sous divers noms : Janken ou Yakyuken au Japon, Kawi-Bawi-Bo en Corée, Jack-En-Poy ou Bato-Bato-Pick aux Philippines, Ko-papír-ollo en Hongrie, etc. Le vainqueur du championnat du monde en 2007 fut l’Américaine Andrea Farina.
Le jeu, s’il n’est joué qu’une seule fois, est une forme de tirage au sort. Aussi, en 2005, le président de la Maspro Denkoh Corporation Takashi Hashiyama, qui ne réussissait pas à choisir si la collection d’œuvres de sa compagnie (comportant des tableaux de Cézanne, Van Gogh et, de Picasso, Le boulevard de Clichy) devait être vendue par Christie’s ou Sotheby’s, organisa une séance de jeu pour fixer sa décision. Les représentants à Tokyo des deux salles des ventes furent conviés à jouer à Pierre-feuille-ciseaux. Christie’s gagna : il avait choisi les ciseaux alors que Sotheby’s avait opté pour le papier ! (Pour plus de détails voir le New York Times du 29 avril 2005). De toutes les parties de Pierre-feuille-ciseaux, c’est sans doute celle à l’enjeu le plus important : la vente portait sur une somme de plus de dix millions de dollars dont plus de 12 % sont revenus à Christie’s.
Parmi les stratégies du type « jouer P avec la probabilité x, jouer F avec la probabilité y, jouer C avec la probabilité z », nommées stratégies mixtes, la stratégie correspondant aux coefficients x = y = z = 1/3 est imbattable : si vous l’adoptez, tout joueur sera, à la longue, ex æquo avec vous ; il ne pourra ni vous battre… ni même perdre s’il le souhaitait. Cette stratégie ne résoudra pourtant pas toutes les questions que pose le jeu. D’une part, un être humain est incapable d’engendrer dans sa tête des choix vraiment aléatoires avec des probabilités fixées à l’avance : celui qui souhaite jouer la stratégie mixte 1/3-1/3-1/3 ne le peut pas ! D’autre part, les joueurs humains utilisent l’information sur les coups déjà joués : ils ne peuvent pas s’en empêcher même s’ils essayent.
Le jeu est en partie psychologique et il y a parfois mieux à faire que la stratégie 1/3-1/3-1/3. Si, par exemple, vous remarquez que votre adversaire n’utilise pas P, alors en jouant invariablement C vous gagnerez toujours (s’il joue F, vous gagnez, s’il joue C, le coup est nul). Bien sûr, il risque de s’apercevoir de votre tactique et de se mettre à jouer P, ce qui vous perdra !
Certains logiciels jouent mieux que les êtres humains, car en repérant les régularités qu’ils adoptent (même quand ils font tout pour ne pas être régulier) leur attitude donne un léger avantage à une machine attentive et bien programmée. Le programme Sagace de Christophe Meyer exploite ainsi les faiblesses humaines.
Comme nous allons le voir dans la suite de cet article, joué sur un graphe, le jeu en apparence simplet engendre des comportements collectifs inattendus et délicats à élucider. Certains mécanismes découverts lors de récentes études expliquent les phénomènes de synchronisation et d’uniformisation et éclairent le maintien de la diversité dans le monde biologique.
Les règles du combat
Dans le jeu sur un graphe, un ensemble de points est fixé, les nœuds du graphe. Sur chacun est placé un symbole de type P (pierre), F (feuille) ou C (ciseaux). Certains couples de points sont reliés par les arcs du graphe.
Cette disposition constitue la configuration initiale dont l’évolution se fait selon un processus aléatoire : un nœud N est choisi au hasard équitablement (chaque nœud a la même probabilité d’être choisi) parmi tous les nœuds et un nœud N’ directement relié à N est choisi au hasard équitablement aussi. Si les deux symboles portés par N et N’ sont de même force, rien ne se produit, sinon le plus faible des deux symboles est remplacé par le plus fort qui occupe alors les deux nœuds N et N’. On recommence, en choisissant un nouveau nœud au hasard, etc. Les combats successifs permettent au gagnant de chaque rencontre d’occuper le terrain de l’adversaire. Ce processus d’évolution est répété un très grand nombre de fois (voir un exemple sur la figure ci-dessous).
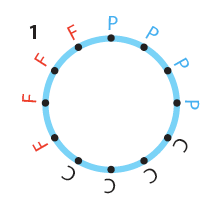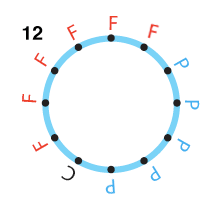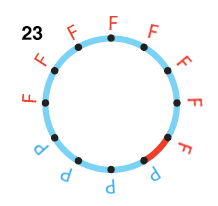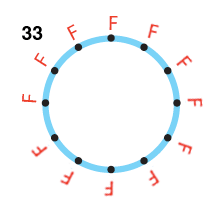 |
| Le jeu sur un anneau. Un anneau est composé de 12 nœuds chacun lié à ses deux voisins. Au départ on place 4 P, 4 C et 4 F. Le jeu consiste à tirer au hasard un arc liant deux nœuds, puis à faire jouer l’un contre l’autre les deux symboles (F l’emporte sur P, P l’emporte sur C et C l’emporte sur F). Le symbole qui gagne occupe alors les deux nœuds. Selon le hasard qui fait jouer ainsi les nœuds les uns contre les autres, soit le jeu préserve la variété, les trois symboles coexistent toujours, soit l’un des symboles finit par disparaître, ce qui entraîne la disparition d’un second symbole, tout l’anneau étant alors occupé par un symbole unique et inamovible (cette occupation unique devient quasi certaine quand le nombre de tirages d’arcs tend vers l’infini). |
Dans cet exemple, le combat revient à choisir au hasard deux nœuds voisins de l’anneau, ce qui conduit soit au statu quo si les nœuds portent le même symbole, soit à un gain de territoire pour le plus fort. Si tout s’équilibrait, les zones ne feraient que se déplacer, chacune gardant en moyenne 4 éléments et tournant dans le sens des aiguilles d’une montre. Cependant, les tirages au sort des combats ne donnent pas des résultats parfaitement réguliers : les tailles des zones tenues par les C, les P et les F fluctuent et ces fluctuations s’amplifient. Inévitablement l’une des trois zones disparaît, ce qui entraîne la disparition d’une seconde zone et il ne reste plus qu’un seul symbole sur tout le terrain. Si la zone qui disparaît en premier est celle des C, les F envahissent tout ; si la zone des P disparaît, les C envahissent l’anneau et si les F disparaissent, les P dominent totalement et définitivement.
Dans le cas d’une configuration initiale irrégulière de C, de F et de P sur un anneau (même beaucoup plus grand) qu’on remplit en tirant au hasard les emplacements des C, des F et des P, l’évolution est de même type. Les déplacements de frontières des différentes zones homogènes amènent assez rapidement une configuration uniforme.
Cette évolution à long terme vers un gagnant définitif (imprévisible) est bien plus générale et se produit pour tout graphe connexe (un graphe connexe est un graphe d’un seul tenant, c’est-à-dire tel que deux nœuds sont toujours reliés par au moins un chemin). Le résultat est : « Pour tout graphe connexe et toute configuration initiale de pierres de feuilles et de ciseaux sur le graphe, la probabilité pour que le système se retrouve au bout d’un temps fini dans un état uniforme (l’un des symboles occupant tous les nœuds) est de 100 pour cent ». (Voir la démonstration exposée ci-dessous sous le titre On peut toujours uniformiser.)
La démonstration du résultat que l’on aboutit toujours à l’uniformisation se fait en deux étapes. On établit d’abord que : « Pour tout graphe connexe et pour toute configuration initiale donnée, il existe un tirage d’arcs conduisant l’un des symboles à tout envahir. » Le raisonnement se fait par récurrence. Prenons un graphe connexe de taille n, et une configuration initiale donnée. Nous allons montrer que pour tout entier p inférieur ou égal à n, il existe une suite de tirages d’arcs conduisant (quand on effectue dans l’ordre tous les combats déterminés par les arcs) à un paquet de p nœuds rattachés (formant un sous-graphe connexe) portant le même symbole S.
- Cela est évidemment vrai pour n = 2.
- Supposons cela vrai pour p < n et considérons la séquence de choix d’arcs qui conduit à un paquet connexe de p symboles S identiques (a).
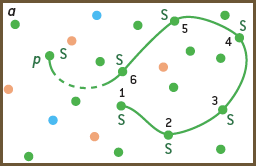
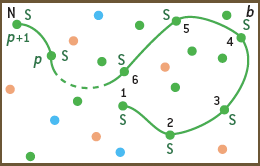
Montrons qu’on peut en déduire une suite de choix d’arcs qui conduit à un paquet connexe de p + 1 symboles identiques (d’après le principe du raisonnement par récurrence, cela nous donnera le résultat). Soit un nœud N, voisin de ce paquet : il y en a au moins un, car le graphe entier est connexe. Si ce nœud N porte le symbole S, nous avons un paquet connexe de p + 1 symboles S et le raisonnement est terminé (b). Supposons alors que N porte un symbole S’ différent de S.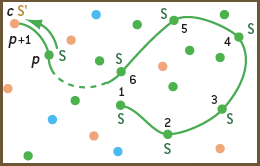
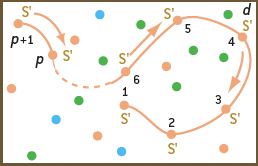
Si S’ est battu par S, on tire l’arc liant le nœud N au paquet de S et l’on a une suite de choix d’arcs (c) qui conduit à un paquet connexe de S de taille p + 1 : le raisonnement est terminé.Si S est battu par S’, on choisit la même séquence d’arcs que celle qui conduisait au paquet de p symboles S, suivie d’une suite de tirages progressifs (d) de ces arcs de proche en proche qui font que S’ envahit tout le paquet de S, lequel devient donc un paquet connexe de p + 1 symboles S’. Cela est possible car le paquet de p symboles S est connexe. On a alors un paquet de p + 1 symboles S’. Dans chaque cas possible, on dispose d’une suite des choix d’arcs conduisant à un paquet connexe de p + 1 symboles identiques. Le raisonnement par récurrence est terminé.
Notons (c’est important pour la seconde partie du raisonnement), que la longueur de la suite d’arcs qui fait passer d’un paquet de p nœuds identiques à un paquet de p + 1 nœuds identiques s’obtient en ajoutant au plus p arcs à celle nécessaire pour avoir un paquet de p nœuds identiques. Au total, si le graphe possède n nœuds, on sera certain d’avoir un graphe uniforme en utilisant une suite d’arcs déterminant les combats successifs de longueur au plus 1 + 2 + 3 + 4+…+ (n – 1) = n(n – 1)/2.
Montrons maintenant que l’uniformisation survient avec une probabilité de 100 %. Cette seconde partie du raisonnement utilise l’évidence probabiliste qu’en répétant un tirage au hasard dans l’attente d’un événement ayant une probabilité non nulle de se produire il finit par se réaliser, ou plus exactement, il se réalise « à l’infini » avec une probabilité de 100 % (en lançant un dé indéfiniment, vous finirez par tomber sur un 6 : s’il est possible, en théorie, de ne jamais avoir de 6, cet événement a une probabilité nulle : si l’on attend longtemps on est certain d’avoir un 6).
Partant d’un graphe de n nœuds dans une configuration donnée, nous savons qu’il existe une suite d’arcs qui uniformise le graphe. Cette suite a une longueur inférieure à n(n – 1)/2. La probabilité qu’un arc donné soit choisi lors d’une étape du processus d’évolution aléatoire est plus grande que 1/(nk) (un nœud est choisi avec une probabilité 1/n et un voisin avec une probabilité 1/k au plus, où k est le nombre maximum de voisins que possède un nœud du graphe). La probabilité pour qu’une suite d’arcs qui uniformise le graphe soit choisie est donc supérieure à (1/nk)n(n – 1)/2, un nombre strictement positif. À l’infini, la probabilité pour qu’au moins une fois une séquence conduisant à l’uniformisation soit choisie est donc de 100 %.
Notons que cela n’interdit pas qu’il existe des suites de tirages particuliers assurant le maintien indéfini des trois symboles sur le graphe (tout comme si vous lancez un dé, vous pouvez obtenir une série ne comportant que des 6). Si l’on considère le graphe circulaire envisagé plus haut et que les arcs sont tirés les uns après les autres en tournant dans le sens des aiguilles d’une montre, il restera toujours des exemplaires des trois symboles. Le sens du résultat d’évolution à long terme est que ce type de suites de tirages préservant la diversité possède une probabilité nulle de se poursuivre à l’infini.
Vérification expérimentale
Nous allons voir que la réalité expérimentale est encore plus intéressante que la théorie mathématique qui indique un peu sèchement qu’au bout d’un certain temps, le système s’uniformise totalement.
Nous allons d’abord observer l’évolution de graphes complets, c’est-à-dire de graphes dont chaque nœud est relié à chaque autre (graphes ayant donc n(n – 1)/2 arcs pour n nœuds). De façon à visualiser les changements nous utilisons une grille carrée où deux cases sont liées qu’elles soient côte à côte sur le dessin ou qu’elles ne le soient pas.
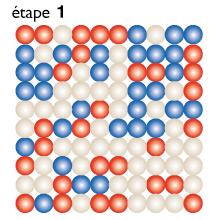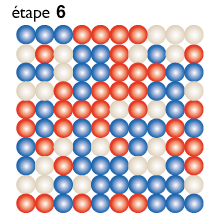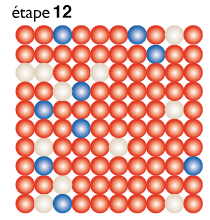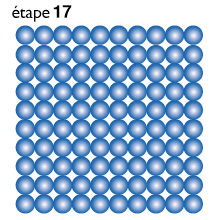 |
| Le jeu sur un graphe complet (où chaque nœud est relié à chaque autre). Pour visualiser l’évolution, on représente le graphe comme si les nœuds étaient disposés sur un damier. On part d’une configuration aléatoire des trois symboles Pierre, feuille, ciseaux (on utilise pour chacun une couleur, rouge, blanc ou bleu). On représente l’évolution en dessinant une étape du graphe tous les 100 combats. Dans un premier temps, le graphe reste à peu près homogène avec 33 pour cent de chacun des symboles. Au bout de 10 étapes (donc 1 000 combats sur un arc) la couleur bleue domine. Deux cents combats plus tard le rouge domine. Puis c’est le blanc, puis le bleu, cette fois définitivement. Dans le cas de graphes de taille plus grande, la phase d’uniformisation partielle avec domination cyclique d’un symbole dure plus longtemps avant la victoire définitive d’un des symboles. Les simulations de cette figure ont été réalisées par Rémi Dorat. |
La figure ci-dessus représente l’évolution d’un graphe complet de cent nœuds. On part d’une configuration aléatoire : rouge pour le symbole Pierre, blanc pour Feuille, bleu pour Ciseaux. Puis on tire successivement 100 arcs du graphe où les combats correspondants sont joués, ce qui donne une nouvelle répartition. Au bout de 17 étapes de 100 combats aléatoires (donc 1 700 combats) le graphe est devenu uniformément bleu : les Ciseaux ont gagné. On voit cependant que l’évolution est passée par une phase d’oscillation généralisée : sur le dixième dessin, les cases en bleu dominent largement, puis sur le dessin 12, c’est au tour des cases rouges d’être majoritaire, avant de laisser la place au dessin 14 aux cases blanches, avant enfin le retour de la domination bleue, cette fois définitive. Pour des graphes complets plus grands, le phénomène de synchronisation est encore plus net et le temps nécessaire avant son interruption par la domination totale d’un symbole devient long car la phase de domination tournante possède un très grand nombre d’étapes.
Ce mouvement tournant où chacun des trois symboles prend le dessus à tour de rôle s’explique partiellement : les Feuilles vivent en exploitant les Pierres, et si les Feuilles se mettent à dominer elles éliminent presque totalement les Pierres ; la situation créée est alors favorable aux Ciseaux qui n’ont plus à craindre les Pierres et qui rencontrent avec une fréquence croissante les Feuilles qu’ils éliminent ; les Ciseaux deviennent donc plus nombreux se multipliant aux dépens des Feuilles. Cette domination des Ciseaux est favorable aux Pierres (plus fort que les Ciseaux) qui deviennent alors majoritaires un peu plus tard, etc.
Reste que cette explication est partielle, car si elle justifie que cela tourne dès que l’un des symboles domine, elle n’indique pas pourquoi l’un des symboles prend rapidement le dessus engendrant l’oscillation synchronisée de tout le graphe : on pourrait imaginer que tout s’équilibre en gros et que les écarts s’effacent vite dès qu’ils se produisent. Nous allons d’ailleurs voir plus loin des graphes d’un autre type où l’équilibre des effectifs est préservé sur des longues périodes.
Dans la nature un tel phénomène de domination cyclique a été plusieurs fois observé. Le lézard californien, Uta stansburiana, étudié par B. Siverno et C. Lively présente ce comportement de domination cyclique car il y a trois sortes de mâles qui semblent pris dans un jeu sans fin de Pierre-feuille-ciseaux sur un graphe. L’accouplement est à l’origine du cycle car, dans cette cruciale compétition, les mâles à gorge orange l’emportent sur les mâles à gorge bleue qui eux-mêmes dominent les mâles à bandes jaunes qui à leur tour sont plus efficaces sexuellement que les mâles à gorge orange.
Les lézards
Le détail de leur curieux jeu est le suivant. Les mâles à gorge bleue possèdent des harems composés de trois femelles environ et ne cherchent à défendre que de petits territoires. Quand ils sont les plus nombreux, les mâles à gorges orange, qui eux sont particulièrement agressifs, réussissent à s’imposer faisant disparaître la presque totalité des mâles à gorge bleue. Les lézards orange ont un tempérament dominant à cause d’une forte concentration en testostérone. Cela les conduit d’ailleurs à constituer des harems ayant jusqu’à sept femelles et à exercer leur domination sur de vastes territoires. Ils se substituent donc aux mâles à gorge bleue dont le nombre faiblit rapidement sans toutefois s’annuler. Interviennent alors les mâles à bandes jaunes qui s’introduisent dans les camps des mâles à gorge orange en se faisant passer pour des femelles. Ces mâles à bandes jaunes deviennent de plus en plus nombreux et un moment arrive où ils sont majoritaires. Cela laisse réapparaître les mâles à gorge bleue, car ceux-ci savent reconnaître les mâles travestis et les chassent. Cela conduit au retour de la situation initiale avec une majorité de mâles à gorge bleue. Comme dans le cas de nos graphes complets un cycle répété de configurations où dominent successivement chacune les trois catégories de mâles se poursuit sans interruption sur les territoires étudiés.
À une échelle bien plus petite, dans le domaine de la chimie, les réactions de Belousov-Zhabotinskii peuvent s’interpréter comme la manifestation d’un jeu de Pierre-feuille-ciseaux joué à l’échelle microscopique entre composants chimiques. Dans ce cas cependant, aucun composant ne devient globalement dominant et c’est plutôt à une coexistence des compétiteurs qu’on assiste, ceux-ci se regroupant par zones homogènes mobiles créant un jeu animé de dessins étonnants qu’on a associé à l’idée même de phénomène complexe.
Il est simple d’obtenir l’équivalent de cette dynamique chimique dans le monde abstrait des graphes du jeu Pierre-feuille-ciseaux : il suffit de ne pas considérer des graphes complets, mais des graphes réguliers comme ceux correspondant aux cases d’un damier. Chaque case est reliée à ses huit voisines et non plus à toutes les cases comme précédemment.
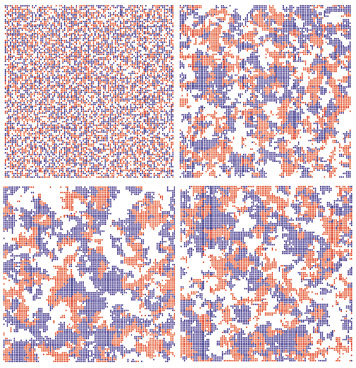 |
 |
| Le jeu sur un graphe-damier où chaque case du damier n’est liée qu’à ses huit voisins. Au départ, le damier est rempli aléatoirement par les trois symboles Pierre, feuille, ciseaux. L’évolution fait apparaître des zones homogènes, qui se déplacent tout en gardant une taille à peu près constante. Aucun symbole ne domine. En théorie, la domination totale et définitive d’un symbole se produit au bout d’un temps fini avec une probabilité de 100 %. En pratique, ce moment vient si tardivement que l’on considère que les trois symboles coexistent. Les relations de domination cyclique entre souches ou espèces dans le monde vivant sont l’une des causes du maintien de la diversité biologique. Le cas du lézard californien Uta stansburiana est frappant car trois variétés de lézards semblent y jouer à Pierre-feuille-ciseaux. |
|
La figure ci-dessus montre des configurations typiques observées après un long moment d’évolution lorsque l’on considère des graphes-damiers de ce type. Cette fois, la représentation du graphe sur un damier prend tout son sens puisque les nœuds du graphe ne sont reliés qu’aux huit nœuds correspondant aux huit cases voisines. Au début, le système est placé dans un état totalement mélangé (1/3-1/3-1/3). Rapidement apparaissent des zones homogènes des trois couleurs et ces zones se déplacent et changent de forme de manière incessante tout en gardant des caractéristiques globales stables : la taille des zones homogènes est à peu près constante, ainsi que leur vitesse de déplacement et le type de motifs dessinés. Ici, aucun symbole ne domine les autres. L’évolution se traduit par des mouvements ininterrompus des frontières interzones. La zone de séparation entre Pierres et Feuilles se déplace car les Pierres reculent devant les Feuilles ; de même, les Feuilles reculent devant les Ciseaux et les Ciseaux devant les Pierres. L’examen détaillé des effectifs montre une oscillation limitée autour de 1/3 de la proportion de chacun des symboles. Cette fluctuation apparaît comme une variation statistique inévitable qui ne prenant pas d’ampleur ne conduira en pratique jamais à la domination d’un symbole.
Temps de convergence différents
Les deux cas rencontrés, oscillation synchronisée de tout le graphe ou formation de zones homogènes mobiles, correspondent à deux modes de la dynamique d’évolution des graphes de Pierre-feuille-ciseaux. Dans les deux types de graphes, nous savons qu’à long terme l’un des états envahit tout. Cependant le temps nécessaire pour que se produise cette domination définitive est très différent dans les deux cas. Dans le cas des graphes complets, ce temps augmente lentement en fonction de la taille du graphe. Dans le cas des graphes-damiers, l’instant de la stabilisation est repoussé bien plus loin, si bien qu’en pratique, le système reste dans un état mixte où les trois symboles coexistent.
La théorie nous indique pourtant que l’un des états finit toujours par dominer ; la simulation nous montre qu’avec les graphes complets cette domination arrive rapidement, alors qu’avec les graphes-damiers, sa venue est tellement éloignée dans le temps que c’est une stabilisation avec coexistence des trois états qu’il faut considérer comme l’évolution normale à moyen terme de la dynamique du graphe. Un travail détaillé d’étude des caractéristiques de ces dynamiques a été mené par Rémi Dorat à coup de simulations massives et prolongées. Il montre que le temps d’uniformisation croit exponentiellement dans le cas des graphes-damiers.
La situation de coexistence des trois symboles est sans doute une explication du maintien de la diversité dans certaines situations biologiques. Le terrain où trois espèces se rencontrent (les dominations se conformant à un schéma circulaire du type Pierre-feuille-ciseaux), est assimilable à un graphe de type graphe-damier. La dynamique de domination montre alors sur le terrain des motifs plus ou moins semblables à ceux vus lors des simulations.
Benjamin Kerr, Margaret Riley, Marcus Feldman et JM Bohannan, dans un article de la revue Nature, proposent une telle interprétation de leur expérience réalisée avec trois souches d’Escherichia coli en relation non-transitive comme les symboles Pierre-feuille-ciseaux. La conclusion de leur étude est conforme à ce qui est montré par les simulations. Lorsque l’espace où est réalisée l’expérience est petit et, plus généralement, lorsque les relations entre souches sont assimilables à celle décrite par un graphe complet, l’une des souches domine rapidement. En revanche, lorsque les interactions se déroulent sur un espace plus grand, cette fois assimilable à un graphe de type damier, les trois souches coexistent avec des mouvements des zones occupées par chacune d’elles, mouvements assez semblables à ceux vus lors des simulations.
Des études sur des graphes intermédiaires entre les graphes complets et les graphes damiers ont été réalisées par György Szabó, Attila Szolnoki, Rudolf Izsák. Divers phénomènes de transition de phases ont pu être mis en évidence, et ils permettent de mieux comprendre toutes ces dynamiques discrètes nées d’un jeu élémentaire. La science n’a jamais fini d’étudier les jeux : même les plus simples suggèrent des modèles explicatifs utiles.
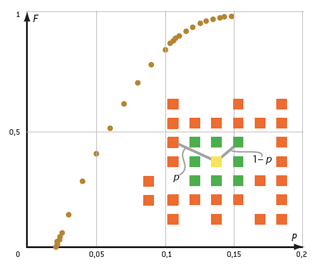
On définit une famille continue entre le jeu sur un graphe complet et le jeu sur un graphe-damier. On se fixe un paramètre p entre 0 et 1. À chaque coup on choisit un premier nœud N au hasard uniformément parmi tous les nœuds. Pour le second nœud N’, on choisit entre deux méthodes A et B, la méthode A choisie avec une probabilité p et la méthode B avec une probabilité 1 – p. Si la méthode A est choisie on prend pour N’ un nœud quelconque du graphe. Si la méthode B est retenue, on choisit N’ parmi les huit voisins de N. Les nœuds N et N’ ainsi déterminés livrent alors combat.
Pour p = 0, tout se passe comme quand on jouait au jeu sur un graphe-damier, pour p = 1, comme si on jouait sur un graphe complet. Pour p assez petit (jusqu’à 0,002) l’évolution du graphe se fait en préservant un bon mélange : les trois symboles restent présents en proportion équilibrée 1/3-1/3-1/3. Lorsque p se trouve entre 0,002 et 0,15 la proportion de chaque symbole fluctue dans le système, ce que l’on mesure par un paramètre de fluctuation F (F = 0, pas de fluctuation ; F = 1, variation maximale des effectifs). Au-delà de 0,15 le système devient violemment oscillant comme dans le cas d’un graphe complet : chacun des symboles domine à tour de rôle, le graphe passant par des états où un symbole occupe la quasi-totalité du graphe, toutes les cases du graphe sont synchronisées (ces simulations ont été menées par A. Szolnoki et G. Szabó).
- R. DORAT, Étude de la domination cyclique sur les graphes. Publication du Laboratoire d’Informatique Fondamentale de Lille, 2007.
- C. MEYER, Sagace
- G. SZABÓ, A. SZOLNOKi, R. IZSÁK, Rock-scissors-paper Game on Regular Small-world Networks J. Phys. A: Math. Gen. 37 (2004) 2599–2609
- B. SIVERNO, C. M. LIVELY, The Rock-paper-scissors Game and the Evolution of Alternative Male Reproduction Strategies, Nature, vol 380, pp. 240-243, 1996
- B. KERR, M. RILEY, M. FELDMAN, J. M. BOHANNAN, Local Dispersal Promotes Biodiversity in a Real-life Game of Rock–paper–scissors, Nature, vol 418, pp. 171-174, 11 july 2002.
- A. SZOLNOKI, G. SZABÓ, Phase Transitions for Rock-scissors-paper Game on Different Networks, Phys. Rev. E 70, 2004.
Une première version de ce document est parue dans la rubrique « Logique et calcul » de la revue Pour la Science n° 364 de février 2008.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Paul Delahaye
Professeur émérite d'informatique à l'Université des Sciences et Technologies de Lille (Lille 1) et chercheur au Centre de recherche en informatique, signal et automatique de Lille (CRIStAL).