Prédire le comportement des cellules avec la modélisation booléenne

Chacun de nous est issu d’une cellule unique, qui s’est récursivement divisée en millions de cellules, qui, de manière très organisée, ont progressivement pris une fonction particulière : sang, peau, neurone, gras, os, œil, etc. Une fois sa fonction établie, une cellule n’en change en général jamais, du moins naturellement. Cependant, certaines cellules, notamment dans le sang, peuvent adapter leur fonction en réponse à différents stimulus qui apparaissent dans leur environnement. Notre corps abrite également des cellules « pluripotentes », c’est-à-dire qui n’ont pas encore une fonction complètement définie, pour permettre de combler certains manques, au besoin.

La compréhension des processus biologiques de différenciation et de reprogrammation cellulaire, menant une cellule à adopter une certaine fonction, est une problématique fondamentale de la biologie. Dans les années 2000, des expériences ont montré qu’il est possible de perturber des cellules humaines prélevées sous l’épiderme pour les transformer en neurones. Ces expériences, qui ont valu un prix Nobel à Shinya Yamanaka en 2012, reposent sur l’activation de gènes qui vont mettre la cellule dans un état pluripotent, à partir duquel on peut forcer sa différenciation en neurone. La reprogrammation cellulaire ouvre d’importantes perspectives en médecine pour pouvoir générer des cellules manquantes à partir de cellules abondantes.

La fonction d’une cellule résulte de nombreux facteurs (on parle de son phénotype), dont sa forme et sa composition. Une cellule possède une membrane extérieure, possiblement un noyau, de l’ADN, des ARN, des protéines, etc. La connaissance actuelle ne permet malheureusement pas de décrire avec précision l’ensemble des composés et réactions d’une cellule. L’ADN des cellules animales contient des milliers de gènes et les interactions entre les protéines qu’ils génèrent ne sont pas toutes connues, et encore moins la vitesse de ces interactions.

Pour appréhender le comportement des cellules et tenter de valider ou infirmer certaines hypothèses biologiques, les chercheurs conçoivent et analysent des modèles mathématiques et informatiques d’une partie des mécanismes qu’ils jugent importants. Selon le niveau de précision choisi, ces modèles décrivent l’évolution dans le temps du nombre d’exemplaires de chaque molécule, de leur concentration, ou simplement de leur présence. Ces modèles peuvent prendre de nombreuses formes, comme des systèmes d’équations différentielles, des graphes avec des règles de réécriture… ou des formules logiques.

Introduite au cours des années 1960, la modélisation booléenne des systèmes biologiques donne une vision du comportement des cellules qui pourrait paraître simpliste : au lieu de quantifier la concentration des molécules, ou de les compter, ces modèles considèrent que les molécules sont soit suffisamment présentes (VRAI/OUI/1), soit pas assez (FAUX/NON/0), pour interagir avec le reste du système. Cette modélisation, formalisée par les réseaux booléens, est actuellement largement employée pour modéliser les interactions entre les gènes, ainsi que leurs signalisations (en réponse à l’activation de capteurs sur la membrane). En effet, ces modèles demandent un niveau de connaissance qui est proche de celui possédé actuellement en biologie, tout en apportant un éclairage sur les gènes et protéines jouant un rôle clé dans les processus cellulaires étudiés.

Et comme nous allons le voir, les comportements décrits par un simple modèle booléen sont tout sauf simplistes !

Réseaux d’influences : amis, ennemis, et cycles

Pour simplifier les choses, mettons de côté les gènes et protéines, et considérons deux individus dont nous modélisons l’humeur : heureux ou triste.

Prenons la situation où ces deux individus s’apprécient beaucoup, et où l’humeur de l’un va fortement influencer l’humeur de l’autre : si mon ami est heureux, je deviens heureux ; s’il est triste, je deviens triste.

Que se passe-t-il dans le cas où l’un des deux est heureux mais l’autre est triste ? Imaginons qu’ils conversent au téléphone : si l’individu heureux parle en premier, annonçant la bonne nouvelle, le second individu va devenir heureux à son tour. Et tout le monde restera heureux. Mais si c’est l’individu triste qui prend la parole en premier, alors tout le monde va devenir et restera triste.

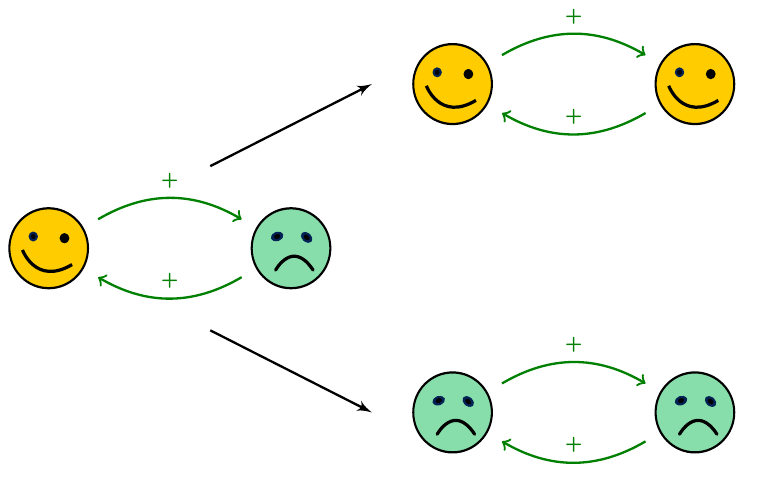
Nous avons affaire ici à un système multi-stationnaire : partant d’une configuration instable (un heureux et un triste), le système peut évoluer vers deux régimes de fonctionnement très différents, sans possibilité de marche arrière ou de changer d’avis. On peut y voir un phénomène de différenciation.

Prenons maintenant le cas où l’amitié n’est pas réciproque : l’individu de droite apprécie beaucoup l’individu de gauche, ce dernier le détestant cordialement. Si quelqu’un que je déteste est triste, je deviens heureux, et son bonheur m’attriste. Repartons de la configuration où un individu (celui de gauche par exemple) est heureux, et l’autre triste. Pour l’individu de gauche, tout va bien : son ennemi est triste. Et de même pour l’individu de droite, qui devient alors heureux. Ce qui rend triste l’individu de gauche, qui rendra à son tour l’individu de droite triste, ce qui rendra heureux l’individu de gauche : retour au point de départ.

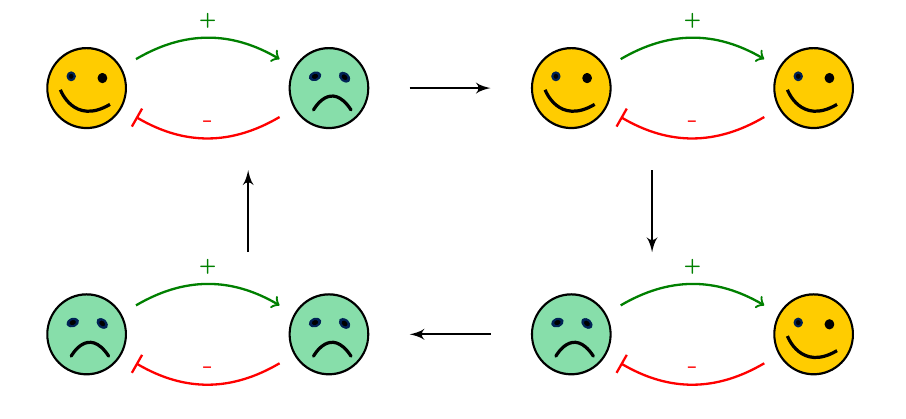
Notre système est dans ce que l’on peut appeler un régime oscillatoire stable : il va osciller pour toujours entre ces 4 configurations. Ces phénomènes d’oscillation se retrouvent dans de nombreux processus biologiques, comme le cycle cellulaire, qui rythme les étapes de la vie des cellules et de leurs divisions, et le cycle circadien, régulant l’horloge interne de l’organisme.

Nous voyons qu’avec seulement deux individus, modélisés chacun par une seule variable booléenne (heureux ou triste), nous obtenons déjà des comportements intéressants. La différence entre les deux modèles étudiés est un simple changement de signe d’une des influences, et cela se traduit par un comportement totalement différent. L’étude du rôle des signes et des cycles d’influences a abouti à des théorèmes fondamentaux sur la richesse de comportements possibles d’un système, certains théorèmes dépassant le cadre des réseaux booléens et allant jusqu’aux équations différentielles ordinaires.

Enfin, reprenons le premier exemple : que se passe-t-il si, au lieu de communiquer par téléphone à tour de rôle, les individus prennent connaissance de l’état de leur ami en même temps (chacun s’envoie un mail et le lit en même temps par exemple). Tout est chamboulé ! Les deux individus changeront simultanément d’état ad vitam æternam (la personne triste devient heureuse et la personne heureuse devient triste). Si on autorise les deux modes de communication, le système peut alors commencer par osciller jusqu’au coup de téléphone salvateur qui fera basculer le système dans une des deux configurations stables (tout le monde heureux, ou tout le monde triste).

Ainsi, la façon dont est mis à jour l’état des individus peut influencer fortement les prédictions sur le système. Dans le premier cas de figure (téléphone, un et un seul individu peut changer d’état à la fois), on parle de mise à jour totalement asynchrone, dans le deuxième cas (mail, tous les individus changent d’état à la fois), de mise à jour synchrone, et dans le dernier cas (téléphone et mail, n’importe quel nombre d’individu change d’état à la fois), de mise à jour asynchrone.

Les réseaux booléens

Remplaçons l’état « heureux » par « \(1\) » et l’état triste par « \(0\) », et numérotons chaque individu à partir de \(1\). Le changement de l’état de chaque individu peut s’écrire à l’aide d’une fonction mathématique booléenne prenant en entrée l’état de tous les individus du système et renvoyant \(0\) ou \(1\) selon ces états. Dans la suite, nous utiliserons un vecteur binaire pour représenter l’état des individus: \(\mathbf x = 01\) est un vecteur de dimension 2, où \(\mathbf x_1=0\) et \(\mathbf x_2=1\). Dans notre premier exemple (amitié réciproque), la fonction \(f_1\) pour calculer le nouvel état de l’individu \(1\) peut s’écrire comme \(f_1(\mathbf x) = \mathbf x_2\) (l’individu 1 devient heureux (1) si l’individu 2 est heureux ; triste (0) si l’individu 2 est triste). Ainsi, \(f_1(01) = f_1(11) = 1\) et \(f_1(10)= f_1(00) = 0\). La fonction associée à l’individu \(2\) est \(f_2(\mathbf x)=\mathbf x_1\). Les fonctions \(f_1\) et \(f_2\) forment alors un réseau booléen, et les individus sont appelés les composants du réseau.

Formellement, un réseau booléen à \(n\) composants est défini par \(n\) fonctions \(f_1(\mathbf x)\), …, \(f_n(\mathbf x)\) qui associent à tout vecteur binaire de dimension \(n\) une valeur booléenne : pour tout \(i\in\{1,\ldots,n\}\), \(f_i:\{0,1\}^n \to \{0,1\}\). De manière équivalente, un tel réseau booléen peut s’écrire sous la forme d’une seule fonction \(f : \{0,1\}^n\to \{0,1\}^n\), où \(f(\mathbf x) = f_1(\mathbf x)\cdots f_n(\mathbf x)\). Par exemple, avec notre réseau de dimension 2 défini dans le paragraphe précédent, \(f(01)= f_1(01)f_2(01) = 10\).

Les évolutions possibles d’une configuration \(\mathbf x\in\{0,1\}^n\) se calculent selon une sémantique ou mode de mise à jour. Parmi les nombreux modes de mise à jour étudiés, nous discuterons ici des modes suivants:

• le mode de mise à jour synchrone applique la fonction \(f\) sur la configuration : \(\mathbf x\) va évoluer en \(f(\mathbf x)\) ;

• le mode de mise à jour totalement asynchrone ne modifie l’état que d’un seul composant du réseau: \(\mathbf x\) peut évoluer vers toute configuration \(\mathbf y\) qui diffère de \(\mathbf x\) en une seule composante \(i\in\{1,\ldots,n\}\) et telle que \(\mathbf y_i=f_i(\mathbf x)\).

• le mode de mise à jour asynchrone autorise la modification simultanée de tout sous-ensemble de composants, considérant ainsi à la fois les évolutions synchrones (tous les composants sont mis à jour), totalement asynchrones (un seul composant est mis à jour), et tout intermédiaire (deux à \(n-1\) composants mis à jour) : \(\mathbf x\) peut évoluer vers toute configuration \(\mathbf y\) telle que, pour chaque composant \(i\in\{1,\ldots,n\}\), soit \(\mathbf y_i=\mathbf x_i\), soit \(\mathbf y_i=f_i(\mathbf x)\).

On peut remarquer que les modes de mise à jour asynchrone et totalement asynchrone peuvent faire évoluer une même configuration \(\mathbf x\) de plusieurs manières, selon le choix des composants mis à jour. Ce sont des modes non déterministes.

Un mode de mise à jour permet de calculer la dynamique du réseau booléen \(f\). Cette dynamique peut se représenter par une relation binaire entre les configurations, que nous noterons par une flèche : \(\mathbf x\to\mathbf y\) signifie que la configuration \(\mathbf x\) peut évoluer vers la configuration \(\mathbf y\) en une étape de mise à jour. On note \(\mathbf x\to^*\mathbf z\) si \(\mathbf x\) peut évoluer en \(\mathbf z\) en utilisant zéro étape (\(\mathbf x=\mathbf z\)), une, ou plusieurs étapes de mise à jour (c’est ce que l’on appelle clôture réflexive et transitive de la relation binaire « \(\to\) »).

Revenons à nos amis, où \(f_1(\mathbf x) = \mathbf x_2\) et \(f_2(\mathbf x) = \mathbf x_1\). Partant de la configuration \(10\), deux évolutions totalement asynchrones sont possibles : \(10\to 11\) et \(10\to 00\), ces dernières configurations ne pouvant plus évoluer. En synchrone, en revanche, on obtient \(10\to 01\to 10\) (cycle). Le graphe suivant résume la dynamique asynchrone, où les sommets sont les configurations et les arcs sont les relations de transition, étiquetées avec les composants mis à jour :

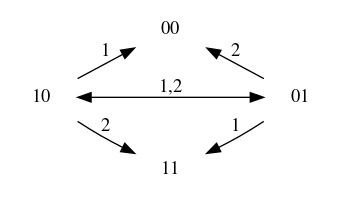
Le second exemple se modélise avec \(f_1(\mathbf x)=\neg \mathbf x_2\) (où « \(\neg\) » est la négation binaire : \(\neg 0=1\) et \(\neg 1=0\)) et \(f_2(\mathbf x)=\mathbf x_1\). Que ce soit en synchrone ou asynchrone, on prédit ici la même évolution :

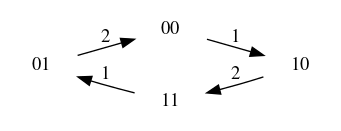
Cette représentation graphique fait apparaître des propriétés dynamiques :

• l’existence d’un chemin d’une configuration \(\mathbf x\) vers une configuration \(\mathbf z\) : on parle d’accessibilité (reachability en anglais). Dans l’exemple de l’amitié réciproque avec la dynamique totalement asynchrone, il existe un chemin de \(01\) vers \(11\), mais aucun chemin de \(01\) vers \(10\).

• des configurations « puits » (sans évolution possible) : les points fixes, qui, avec les sémantiques précédemment définies, correspondent aux points fixes de \(f\), c’est-à-dire les configurations \(\mathbf x\) telles que \(f(\mathbf x)=\mathbf x\). Dans l’exemple de l’amitié réciproque, il y a 2 points fixes en synchrone ou asynchrone : \(11\) et \(00\). Dans l’exemple de l’amitié non réciproque, il n’y a aucun point fixe.

• les composantes fortement connexes terminales : les ensembles de configurations accessibles deux à deux (cycles) dont il n’existe aucun chemin sortant : les attracteurs, dont les points fixes sont un cas particulier. Dans l’exemple de l’amitié réciproque, hormis les deux points fixes, il existe un 3^e attracteur dans la dynamique synchrone, entre les configurations \(01\) et \(10\), qui n’est pas un attracteur en asynchrone. Dans l’exemple de l’amitié non réciproque, le réseau a un unique attracteur avec les 3 modes de mises à jour : l’ensemble des configurations \(00\), \(01\), \(11\) et \(10\).

Les attracteurs modélisent les comportements stables du système : partant de n’importe quelle configuration, le système peut toujours atteindre au moins un attracteur. Une fois dans un attracteur, il ne peut plus en sortir.

Modélisation des réseaux biologiques

Un réseau booléen modélise ainsi la logique d’activation des composants du système. Si l’on revient à notre contexte biologique, cela se traduit par décrire dans quelles conditions un gène va s’activer, en fonction de la présence de ses activateurs (amis) et inhibiteurs (ennemis). Si une partie de cette logique peut se déduire des connaissances actuelles, il manque encore très souvent l’information pour définir précisément les cas où un composant peut s’activer : est-ce qu’il suffit d’un seul facteur de transcription pour activer le gène, ou est-ce que plusieurs sont nécessaires ? Est-ce que certains inhibiteurs dominent l’ensemble des facteurs de transcription ou seulement une sous-partie ?

Admettons maintenant qu’après suffisamment de recherche, nous arrivons à définir un réseau booléen \(f\) fidèle aux connaissances biologiques. Comment le valider ? Nous pouvons par exemple comparer les attracteurs du réseau booléen avec les phénotypes connus du système : un phénotype regroupe un ensemble de facteurs caractérisant une fonction cellulaire, dont par exemple l’expression (ou absence d’expression) de certains gènes. On s’attend alors qu’à chaque phénotype corresponde au moins un attracteur qui reflète les états des gènes associés. Une autre validation possible est de s’assurer que si on observe l’activation de certains gènes au cours du temps, notre modèle arrive à reproduire ces mêmes changements. Mais attention, le choix du mode de mise à jour peut modifier considérablement les prédictions du modèle, et donc sa validation ! Alors, lequel choisir ?

Le mode totalement asynchrone interdit que deux composants changent d’état simultanément, ce qui paraît restrictif ; le synchrone force à ce que tout le monde change d’état simultanément tout le temps, ce qui ne paraît pas réaliste non plus ; l’asynchrone, plus flexible, est-il suffisant ?

La réponse à ces questions dépend de ce qui est modélisé, de la nature des prédictions attendues, et de la manière dont un modèle sera confronté à la réalité pour le valider ou l’infirmer.

Pour des modèles dits « phénoménologiques », cherchant à reproduire des processus généraux comme la différenciation cellulaire, sans forcément relier les composants du modèle à des composants biologiques précis, l’étude des modes de mise à jour est un point fondamental puisqu’il permet de s’abstraire de nombreux mécanismes de régulation temporelle comme le repliement de l’ADN.

Pour des modèles « mécaniques » où les composants du réseau booléen modélisent des composés biologiques précis, dont l’état n’est en réalité pas booléen, nous avons récemment démontré que l’interprétation asynchrone n’est pas suffisante pour rendre compte de la diversité des comportements possibles (voir Paulevé et al., Nature communications, 2020).

La figure suivante illustre un contre-exemple avec un réseau à 3 gènes, dont les influences positives et négatives sont décrites dans la partie (a) :

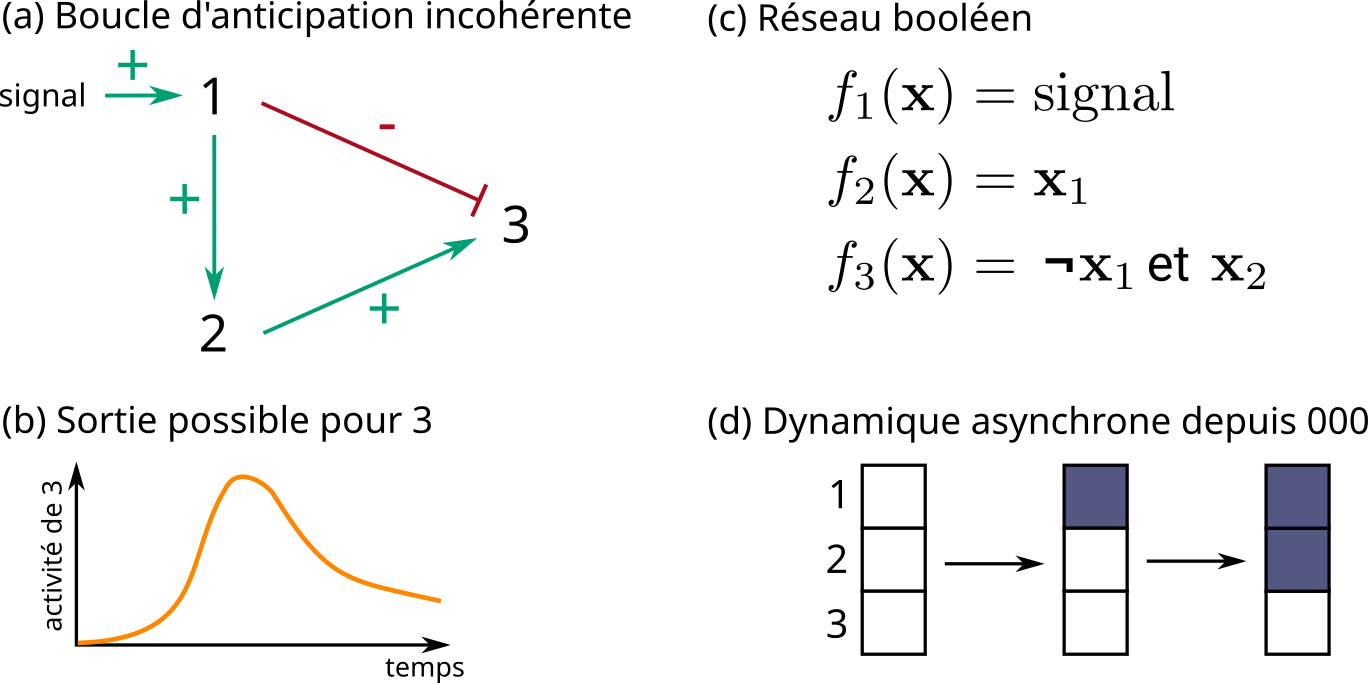
Le gène 1 reçoit un signal qui va progressivement l’activer. Le gène 1 inhibe directement le gène 3 de sortie, mais l’active indirectement via le gène 2. Ce système a été étudié à l’aide de modèles quantitatifs (systèmes d’équations différentielles) et a même été conçu avec de l’ADN de synthèse. Ces études ont montré que, selon les vitesses des influences, l’activation du gène 1 peut aboutir à activer transitoirement le gène 3, comme illustré dans la partie (b) de la figure. En effet, durant l’activation progressive du gène 1, il peut devenir suffisamment actif pour activer le gène 2 qui active à son tour le gène 3, tout en n’étant pas assez actif pour le réprimer directement. Lorsque l’activité du gène 1 dépasse un certain seuil, la répression de la sortie commence et le gène 3 va progressivement se désactiver.

La modélisation de ce système en réseau booléen est donnée dans la partie (c) de la figure. La partie (d) montre la dynamique possible depuis la configuration où tous les gènes sont inactifs (un carré blanc représente le \(0\) et un carré bleu le \(1\)) : cette dynamique est identique en synchrone, totalement asynchrone et asynchrone. Il s’avère impossible de prédire que le gène 3 peut s’activer. Même si cette activation n’est que transitoire dans le système quantitatif, intégrée dans un système plus complexe, elle peut déclencher de nombreuses réactions en cascade, modifiant profondément les prédictions sur l’évolution du système. Et pourtant, le modèle (c) est bien correct…

Heureusement, le problème ne vient pas de la simplification binaire proposée par les réseaux booléens, mais de la sémantique. Nous avons inventé une nouvelle façon d’interpréter les réseaux booléens qui garantit formellement de ne rater aucun changement d’état qui serait possible si on avait une connaissance plus précise du système, et ce sans paramètre supplémentaire (voir Paulevé et al., Nature communications, 2020). Cette sémantique, qualifiée de « Most Permissive » (MP), décompose le changement d’état d’un composant en considérant des pseudo-états dynamiques de croissance et décroissance. Lorsqu’un composant est dans un de ces états dynamiques, la sémantique considère qu’il peut à la fois être considéré comme actif et inactif selon ses influences. Ceci permet de s’abstraire complètement des différences de seuils de concentrations et des échelles temporelles des influences, qui sont rarement connues.

Les changements d’état des composants en MP suivent les règles suivantes. Un composant\(i\) dans l’état \(0\) peut aller dans l’état de croissance ↗ s’il peut lire l’état des composants du réseau de telle sorte que sa fonction \(f_i\) vaille \(1\) : un composant dans un état \(1\) ou \(0\) est lu tel quel, un composant dans un état ↗ ou ↘ est lu au choix comme \(0\) ou \(1\). Une fois dans l’état ↗, il peut changer vers l’état \(1\) sans contrainte, ou aller dans l’état de décroissance ↘ s’il peut lire l’état des composants du réseau de telle sorte que sa fonction \(f_i\) vaille \(0\). De manière symétrique, un composant dans l’état \(1\) peut aller dans l’état ↘ s’il peut lire l’état des composants du réseau de telle sorte que \(f_i\) vaille \(0\). Une fois dans l’état ↘, il peut changer vers l’état \(0\) sans contrainte, ou vers l’état ↗ s’il peut lire l’état des composants de telle sorte que \(f_i\) vaille \(1\).

La figure suivante résume les changements possibles d’états d’un composant du réseau en MP, en précisant leur condition. La fonction \(\gamma\) représente toutes les façons de lire une configuration MP.

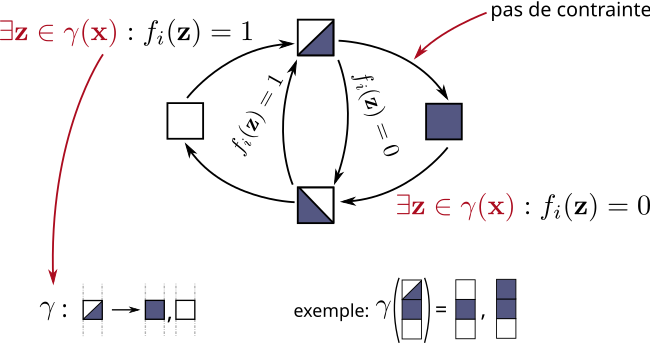
Les carrés avec le coin inférieur-droit en bleu représentent l’état dynamique croissant ↗, et ceux avec le coin inférieur-gauche en bleu l’état dynamique décroissant ↘.

La figure suivante montre une évolution possible du réseau booléen (c) selon la sémantique MP :

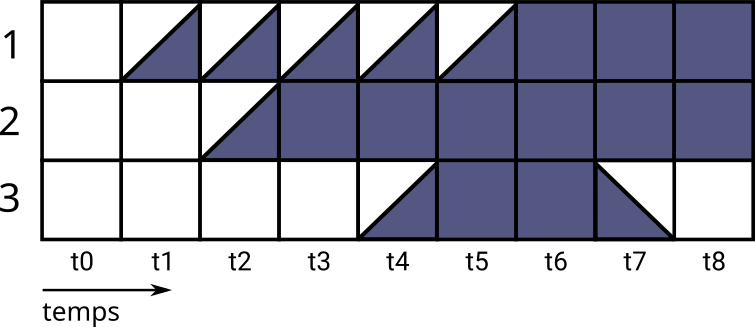
Alors que le gène 1 passe dans l’état croissant (t1), le gène 2 peut s’activer(t2-t3) et à son tour activer le gène 3 qui a le droit de considérer le cas où 1 est inactif pour lui (t4). Une fois que le gène 1 atteint sa pleine activité (t6), le gène 3 va finir par se désactiver (t7-t8).

Cerise sur le gâteau, le calcul des propriétés d’accessibilité et d’attracteur se simplifie grandement avec la sémantique MP, permettant de traiter des modèles avec des centaines de milliers de gènes. En effet, alors que deux configurations peuvent être reliées par un nombre toujours exponentiel de transitions avec les modes de mise à jour synchrone et asynchrone, il existe forcément un raccourci utilisant un nombre de transitions MP linéaire avec le nombre de composants du réseau. De plus, il existe une procédure simple pour trouver ce raccourci. Concernant les attracteurs, il s’avère qu’ils ont toujours une forme particulière en MP qui les rend plus faciles à calculer qu’en synchrone ou asynchrone.

Il est ainsi possible de raisonner formellement avec les réseaux booléens sur les comportements possibles ou impossibles d’un système quantitatif, tel qu’un système biologique. La sémantique MP suggère également qu’il y aurait de nouvelles sémantiques à explorer afin de capturer les comportements de systèmes quantitatifs plus spécifiques.

Pour aller plus loin

La modélisation avec les réseaux booléens touche à de nombreux domaines scientifiques : la combinatoire, la théorie des systèmes dynamiques, la complexité, les méthodes formelles, l’algorithmique, l’intelligence artificielle, l’ingénierie logicielle, la simulation, la biologie théorique, la biologie expérimentale, pour n’en citer qu’une partie.

En biologie, la modélisation informatique aide à comprendre les phénomènes de différenciation cellulaire et la prédiction de cibles pour la reprogrammation des cellules, ce qui est un enjeu central pour de nombreuses applications en immunologie, cancérologie, ou médecine régénérative. La problématique de la construction et de la validation des réseaux booléens avec les données expérimentales et les connaissances à ce jour est actuellement un défi majeur.