
Quarks et simulation numérique
Cet article est devenu obsolète, de par son contenu ou sa forme, il est donc archivé.
Plus d’un comptable froncerait les sourcils s’il apprenait que nous avons fait fonctionner en continu un supercalculateur durant plusieurs années pour n’obtenir qu’une dizaine de résultats. Pourtant, nous n’avons pas perdu notre temps : pour résoudre des problèmes clés de la théorie des particules fondamentales, seul l’ordinateur pouvait venir à bout des tâches que nous lui avions confiées !
Nous nous intéressions particulièrement aux problèmes nés de la chromodynamique quantique, la théorie qui décrit les interactions entre quarks d’une part et l’interaction forte entre hadrons d’autre part. Formulée dans les années 1970, cette théorie de la physique des particules stipule que les quarks s’associent par deux ou trois pour former des hadrons, c’est-à-dire des particules sur lesquelles s’exerce la force nucléaire forte. La famille des hadrons comprend les protons et les neutrons — ils composent les noyaux atomiques — ainsi que d’autres particules moins familières qui apparaissent brièvement dans les accélérateurs de particules ou dans les gerbes de rayons cosmiques. Les expériences consistant à bombarder des hadrons à l’aide d’électrons, afin de sonder la structure interne des particules, ont contribué à corroborer la théorie sur la chromodynamique quantique, qui est devenue l’une des clefs de voûte du Modèle standard, la théorie la mieux admise de la physique des particules.
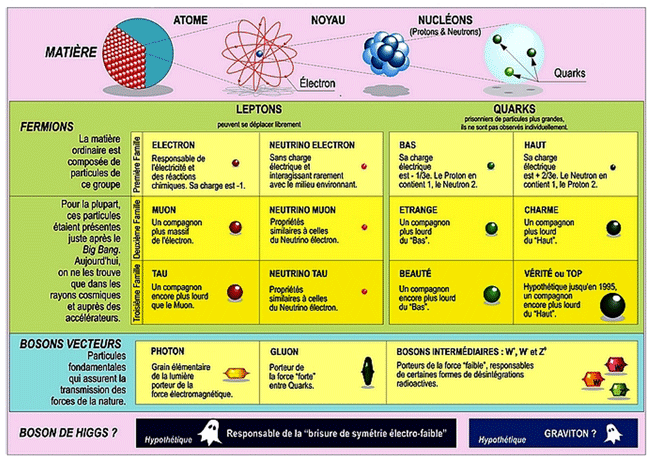
Tableau des particules élémentaires dans le cadre du modèle standard.
Source : Daniel Bonnerue / Wikipédia
Cependant, les résultats étaient imparfaits, car la chromodynamique quantique aurait dû permettre de calculer la masse du proton, du neutron ou de n’importe quel hadron (le problème étant bien de calculer la masse des hadrons et non de la mesurer, ce qui a été fait depuis longtemps ; les masses du proton et du neutron, par exemple, ont été découvertes au début du siècle dernier). Toutefois, la résolution des équations mathématiques requise pour déduire de telles masses de la théorie était largement au-delà des capacités humaines de calcul. Même les ordinateurs les plus rapides des années 1970 auraient mis plus de 100 ans pour faire ces calculs.
Aussi, en 1983, au Centre de recherche IBM de Yorktown Heights, nous avons commencé la construction d’un ordinateur parallèle spécialisé dans la résolution des équations de la chromodynamique quantique. L’ordinateur devait effectuer jusqu’à 11 milliards d’opérations arithmétiques par seconde : il devait ainsi être plusieurs centaines de fois plus puissant que les ordinateurs les plus puissants de l’époque. Aujourd’hui, une telle puissance de calcul n’a plus rien d’exceptionnel : c’est celle de 200 ordinateurs personnels équipés de la dernière puce Pentium de la Société Intel !
En 1991, après huit ans de recherches, nous avons utilisé l’ordinateur pour nos premiers calculs de chromodynamique quantique. Au bout d’un an de calcul, notre ordinateur, GF11, a produit son premier résultat, en déterminant la masse du proton et de sept autres hadrons. Les différences entre nos prévisions et les mesures expérimentales, inférieures à six pour cent, résultaient de l’algorithme utilisé pour les statistiques plutôt que des incertitudes provenant de la théorie elle-même.
 |
 |
|
Le superordinateur GF11 est composé de 566 processeurs qui calculent en parallèle. Le « permuteur » collecte et redistribue les données aux processeurs ; le contrôleur coordonne toutes les activités. Sur la photographie, les processeurs sont les cartes couleur bronze qui coulissent dans les armoires ; les câbles font partie du système contrôleur-permuteur. |
|
En novembre 1995, nous sommes arrivés au terme d’un autre ensemble de calculs, obtenu cette fois en faisant fonctionner l’ordinateur en continu pendant deux ans. En examinant une table de résultats expérimentaux du passé, l’ordinateur détermina la masse et le taux de désintégration d’une particule subatomique insaisissable appartenant à la sous-famille des hadrons, les « boules de glu ». Cette boule de glu, créée lors d’une expérience, n’avait jusque-là pas été reconnue ; c’était la première fois que des calculs massifs identifiaient une nouvelle particule.
Simultanément, ce travail sur les masses des hadrons ainsi que sur la masse et le taux de désintégration des boules de glu a confirmé la chromodynamique quantique. Il nous a fourni une nouvelle façon de traiter les problèmes de physique fondamentale. En raison des coûts exorbitants des accélérateurs de particules et de la complexité des problèmes théoriques actuels, les calculs numériques deviendront, dans certains cas, le seul recours possible pour les physiciens.
Les quarks et le champ de couleur
Pourquoi les quarks ont-ils un comportement si complexe ? En partie, parce qu’ils s’associent de multiples manières. Il existe six « saveurs », c’est-à-dire six sortes de quarks : u pour up (haut), d pour down (bas), s pour strange (étrange), c pour charmed (charmé), t pour top (vérité) et b pour bottom (beauté). Chacun de ces quarks peut porter l’une des trois « couleurs de charge » dénommées rouge, vert et bleu.
Ainsi, les caractéristiques des quarks sont décrites par 18 combinaisons possibles de saveurs et de couleurs. En outre, à chaque type de quark correspond un antiquark (de même masse mais de charge électrique opposée et de charge de couleur complémentaire). L’antiparticule nommée antiquark est donc caractérisée par son antisaveur et son anticouleur. La chromodynamique quantique stipule que les quarks ou les antiquarks ne peuvent être isolés ; aussi les physiciens déduisent-ils leurs propriétés en observant les interactions entre des paires de hadrons ou entre des hadrons et d’autres particules élémentaires, tels les électrons et les photons.
La chromodynamique quantique est complexe, parce que les charges de couleur engendrent un champ confinant, nommé « champ chromoélectrique » : les charges de couleur des quarks sont analogues aux charges électriques ordinaires, qui créent un champ électromagnétique autour des particules chargées. Tout comme un champ électromagnétique lie les électrons chargés négativement aux charges positives présentes dans le noyau d’un atome, le champ chromoélectrique lie les quarks et les antiquarks en hadrons (la matière et l’antimatière peuvent coexister pendant un temps limité avant de s’annihiler mutuellement). La chromodynamique quantique prévoit donc une vaste gamme de hadrons, qui résultent des différentes combinaisons possibles entre les 36 types de quarks et d’antiquarks existants.
Le champ chromoélectrique est toutefois plus complexe que le champ électromagnétique : il peut interagir fortement avec lui-même pour créer des agrégats variés. Dans un hadron, le champ se condense en une corde dense et fine qui contient une partie notable de la masse totale du hadron. C’est une des raisons pour lesquelles la masse d’un hadron ne peut être obtenue en additionnant simplement les masses des quarks qu’il contient. C’est aussi, en dernière analyse, la raison pour laquelle il est si difficile de déterminer la masse des hadrons par la chromodynamique quantique.
Les cordes du champ chromoélectrique peuvent aussi former une boucle fermée, créant ainsi une particule sans quark ni antiquark. Comme le champ chromoélectrique « colle » les hadrons faits de quarks, les particules composées uniquement de ce champ sont nommées des boules de glu.
Un réseau d’espace
La prévision de phénomènes physiques nouveaux à partir de la chromodynamique quantique impose une interprétation mathématique plus spécifique du comportement des quarks et du champ chromoélectrique. Les méthodes numériques appliquées sont toutes fondées sur une formulation de la théorie proposée en 1974 par Kenneth Wilson, de l’Université de l’Ohio.
K. Wilson a proposé de décrire le changement de la configuration des quarks et du champ chromoélectrique dans le monde réel au cours du temps. Par exemple, dans une configuration, un quark entrerait en collision avec un autre quark, à midi pile, à une vitesse de un mètre par seconde, le champ chromoélectrique étant nul partout dans l’espace. Dans une autre configuration par exemple, les quarks repartiraient dans des directions opposées à deux heures de l’après-midi et à 90 degrés de leur trajectoire initiale, le champ chromoélectrique étant alors devenu non nul en certains points de l’espace. La théorie de K. Wilson permet de calculer la probabilité pour la transition entre les deux configurations de survenir entre midi et 14 heures. En permettant ce calcul des probabilités de transition, la chromodynamique quantique donne des prévisions.

Les calculs de chromodynamique quantique imposent de décrire l’espace-temps par un réseau à quatre dimensions. Pour être le plus proche possible de la réalité, on fait les calculs sur des réseaux de plus en plus serrés, et de plus en plus gros. On améliore ainsi la précision globale de la représentation (ici, celle d’un tore).
Infographie : Michael Goodman
La formulation de K. Wilson s’applique à un monde assez inhabituel, où l’espace-temps, continu et illimité, est représenté par un réseau, c’est-à-dire une sorte de damier à quatre dimensions (trois dimensions pour l’espace et une pour le temps). On limite l’étendue de ce réseau, de sorte que l’ensemble de l’espace et du temps est décrit par un nombre fini de points ; à chaque point correspond une configuration spécifique des quarks et du champ chromoélectrique. C’est la raison pour laquelle la formulation de K. Wilson est nommée chromodynamique quantique sur réseau.
Comme le monde ainsi modélisé diffère du monde réel, on cherche une meilleure description en considérant des réseaux de plus en plus serrés et de plus en plus gros : on fait tendre vers zéro la distance entre deux nœuds adjacents du réseau et vers l’infini le volume du réseau.
En principe, on doit additionner un très grand nombre de termes pour obtenir la probabilité d’une transition : à chaque manière de construire un tableau, correspond un terme de la somme. Plus précisément, les colonnes et les lignes du tableau correspondent respectivement aux points du réseau et aux configurations de quarks et du champ chromoélectrique en chaque point.
Le nombre de tableaux possibles est vertigineux : pour chaque point du réseau, on doit utiliser 32 nombres réels pour représenter le champ chromoélectrique, de telle sorte que, pour un réseau de seulement dix unités de côté, dans chaque dimension, le tableau du champ est composé de 320 000 nombres réels (32 nombres pour chacun des 10 x 10 x 10 x 10 points du réseau). Pour les besoins d’un calcul d’ordre de grandeur, négligeons la nécessité de conserver en mémoire la trace des quarks au cours des calculs et supposons (ce qui n’est pas exact) que les 320 000 nombres valent seulement zéro ou un. Chaque tableau possible serait composé d’une série de 320 000 zéro et un, et le nombre total de ces tableaux possibles – c’est-à-dire le nombre total de termes dans la somme de K. Wilson – serait égal à 2320 000, un nombre qui s’écrit en système décimal par un 1 suivi de 96 000 zéros !
Casino et mécanique quantique
En 1979, au Laboratoire de Brookhaven, plusieurs chercheurs (Michael Creutz, Lawrence Jacobs et Claudio Rebbi) reprirent une idée de K. Wilson et inventèrent une méthode numérique pour venir à bout de ces calculs longs et complexes. Leur méthode est une forme d’« intégration de Monte-Carlo », qui consiste à faire une approximation de la solution d’un problème complexe par le biais d’un échantillonnage statistique, un peu comme on utilise des sondages pour prédire le résultat des élections.
Plutôt que d’additionner la totalité des termes associés aux configurations possibles du réseau, on effectue un échantillonnage et l’on estime la somme cherchée en additionnant un petit nombre de termes sélectionnés aléatoirement. Par cette méthode, on traite le cas d’un réseau de dix unités de côté en « seulement » 20 milliards d’opérations arithmétiques. En 1979, un ordinateur de puissance moyenne effectuait un demi-million d’opérations arithmétiques par seconde : la méthode de Monte-Carlo donnait alors une approximation suffisamment précise en moins d’un jour.
Pour résoudre les équations de la chromodynamique quantique sur des réseaux, les physiciens utilisent la méthode de Monte-Carlo. Ils déterminent ainsi des « amplitudes de transition », c’est-à-dire la probabilité que les quarks et le champ chromoélectrique évoluent vers un état final particulier.
Quand on jette un dé, l’amplitude de transition est simplement la probabilité d’apparition d’une des faces. Supposons maintenant que le dé soit pipé et que vous ignoriez quelles faces sont chargées. Le résultat dépend de l’orientation du dé avant le jet et du temps pendant lequel il est secoué avant d’être lancé.

Un lancer de dé ne contribue à l’amplitude de transition 1-6 que si un six est finalement obtenu (premier et troisième jets).
Infographie : Pour la Science
La méthode de Monte-Carlo consiste à lancer le dé et à observer ce qui se passe, comme un joueur le ferait lors d’une véritable partie dans un casino (d’où le nom de la méthode). Pour trouver l’amplitude de transition du dé entre la position avec un point sur la face visible et la position avec six points une minute plus tard, par exemple, vous tiendriez le dé avec la face à un point en l’air, le secoueriez pendant un moment et le jetteriez de sorte qu’il s’arrête au bout d’une minute ; puis vous regarderiez si la face à six points est sortie ou non. Vous répéteriez l’opération plusieurs fois. La proportion de lancers qui aboutissent à un six serait l’amplitude de transition désirée.
En chromodynamique quantique, la détermination des amplitudes de transition n’est pas très différente. Initialement, on spécifie la configuration du champ désirée au temps initial (ce qui correspond à l’orientation particulière du dé dans la main). L’ordinateur crée alors une série temporelle aléatoire de champs selon la dimension temps du réseau (il secoue le dé), et il s’arrête dans une configuration de champ au temps final spécifié (il lance le dé). On examine alors le résultat pour déterminer si la configuration finale souhaitée a été obtenue (on regarde si un six est sorti). La proportion de tirages conduisant à la configuration finale spécifiée donne l’amplitude de transition recherchée. Une fois l’amplitude de transition trouvée, on en déduit les masses des hadrons.
Dans les calculs de chromodynamique quantique, on confie à chacun des 566 processeurs parallèles de l’ordinateur GF11 une partie des calculs. Les algorithmes qui engendrent des champs chromoélectriques aléatoires et déterminent les mouvements des quarks sont intégrés dans des programmes qui déterminent en détail les calculs, dans la partie confiée à chaque processeur. En chaque point du réseau, le processeur « secoue » le champ chromoélectrique – l’analogue chromodynamique de l’agitation du dé – d’une façon qui dépend du champ en ce point et aux sites voisins.
Avec le GF11, nous avons comparé des masses calculées aux masses observées dans le monde réel, où la distance entre deux points adjacents du réseau tend vers zéro et où le volume du réseau tend vers l’infini. Nous avons calculé les masses pour des volumes et des mailles de réseau différents. Tout d’abord, nous avons considéré de grands volumes, en choisissant une maille de 1,5 × 10-14 centimètre, connue pour donner des résultats pas trop éloignés des masses limites obtenues quand la maille tend vers zéro. Nous avons alors calculé les masses des hadrons pour différents volumes du réseau. Les résultats obtenus pour un réseau de 16 unités de côté étaient cohérents à cinq pour cent près avec les valeurs limites pour un réseau infini, et à un pour cent près pour un réseau de 24 unités de côté. Puis nous avons entrepris de faire tendre la maille du réseau vers zéro. Nous avons calculé les masses des hadrons sur un réseau de 24 unités de côté et de maille égale à 1 × 10–14 centimètre, puis sur un réseau de 32 unités de côté et de maille égale à 0,75 × 10–14 centimètre, toujours avec un volume de 16 unités de côté. Ces trois calculs nous ont permis d’extrapoler nos prédictions à la limite où la maille du réseau tend vers zéro.
Malheureusement, on n’obtenait ce résultat qu’en appliquant une forme simplifiée de la chromodynamique quantique, dans laquelle on ne tenait compte que du champ chromoélectrique et pas des quarks. Avant d’effectuer des calculs similaires en utilisant la théorie complète, on a dû résoudre une série de problèmes techniques. En 1981, Federico Fucito, Enzo Marinari et Giorgio Parisi, à Rome, Donald Petcher et moi-même, à Yorktown Heights, et d’autres physiciens avons proposé des versions de l’algorithme de Monte-Carlo intégrant la présence de quarks. Ces divers algorithmes comprenaient notamment une mesure de la difficulté pour les quarks et les antiquarks de passer de leur configuration initiale à une configuration finale.
La prise en compte des quarks et des antiquarks imposait toutefois un accroissement excessif du nombre d’opérations arithmétiques : le plus rapide des ordinateurs de l’époque n’aurait donné des résultats réalistes qu’en un siècle et demi de calcul ininterrompu !
Cette difficulté provenait de l’énergie de chaque configuration de quarks et du champ chromoélectrique : dans toute région de l’espace où un champ chromoélectrique est présent, une énergie importante est émise quand des paires de quarks-antiquarks apparaissent fugacement, puis disparaissent.
En 1981, j’ai imaginé une technique d’« approximation de valence » pour compenser cet effet : on supprime la contribution des paires de quarks-antiquarks en divisant toutes les charges de couleur par une constante « chromodiélectrique ». Nous avons ainsi découvert qu’on atteignait une bonne description du monde réel en considérant des réseaux de 32 unités de côté par dimension ; 1017 opérations arithmétiques permettaient d’effectuer un calcul complet.
Toutefois, les ordinateurs les plus rapides du début des années 1980 exécutaient 40 millions d’opérations arithmétiques par seconde, soit 1015 opérations par an. Par conséquent, même avec la méthode de l’approximation de valence, le calcul des masses des hadrons aurait pris 100 ans. C’était encore excessif !
Enfin des prévisions
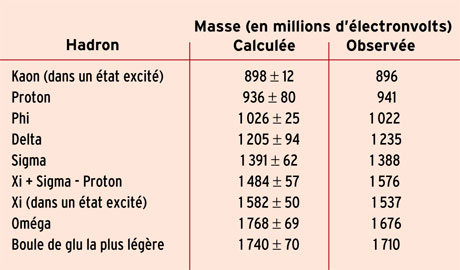
Les masses calculées des hadrons sont comparées aux valeurs mesurées expérimentalement. Les calculs sont plus simples quand on additionne les masses de la particule Xi, de la particule sigma et du proton
Source : D. Weingarten
En 1983, Monte Deneau, John Beetem et moi-même avons entrepris la construction d’un ordinateur spécialisé dans les calculs de chromodynamique quantique. Nous visions une puissance de 11 milliards d’opérations arithmétiques par seconde, soit 11 gigaflops (d’où le nom de l’ordinateur : GF11).
Pour obtenir une machine 250 fois plus rapide que les meilleurs ordinateurs de l’époque, nous avions prévu de faire travailler 566 processeurs en parallèle. La fréquence d’horloge, correspondant à la vitesse à laquelle un processeur peut exécuter une addition ou une multiplication, devait être égale à 50 milliards de Hertz, et chaque processeur, d’une capacité de 20 mégaflops, devait envoyer une donnée aux autres processeurs toutes les 200 nanosecondes (plusieurs dizaines de superordinateurs d’aujourd’hui sont plus rapides que GF11 ; le plus rapide de tous est environ dix fois plus rapide). Avec l’aide de James Sexton, j’ai réalisé les programmes du système d’exploitation, du compilateur et un jeu de programmes de diagnostic du matériel. Puis nous avons collaboré avec un groupe important du Centre de recherche IBM de Yorktown Heights pour la mise au point finale de la machine.
À la fin de 1991, nous avons fait les premiers calculs de masses hadroniques. Nous avons d’abord étudié les masses de 11 hadrons formés de combinaisons des trois saveurs des quarks et des antiquarks les plus légers, u, d et s. Les quarks u et d sont les constituants des neutrons (un u et deux d) et des protons (deux u et un d). Les quarks s sont quant à eux présents dans un grand nombre de hadrons instables. Nous avons calculé la masse de chaque hadron pour des réseaux de tailles diverses. Dans chaque cas, nous avons ajusté certains paramètres en utilisant la masse connue de trois hadrons : nous avons modifié ces paramètres jusqu’à ce que la masse calculée concorde avec la masse connue.
Il nous est ainsi resté huit prédictions de masse à faire pour chaque type de réseau. Pour trouver la valeur des masses aux limites, quand le réseau a un volume infini et une maille de longueur nulle, nous avons extrapolé les prédictions obtenues pour des réseaux de volume croissant et de maille décroissante.
La différence entre chaque prédiction et la masse déterminée expérimentalement a été, dans tous les cas, inférieure à six pour cent, ce qui était dans la gamme des incertitudes prévues, du fait de l’utilisation de la méthode de Monte-Carlo. Bien que ces résultats aient été obtenus dans le cadre de l’approximation de valence, cette approximation n’aurait probablement pas fourni huit résultats corrects si la chromodynamique quantique avait été fausse. Autrement dit, nos résultats confirment à la fois les prédictions de masse de la chromodynamique quantique et la fiabilité de l’approximation de valence.
Plus récemment, nous avons exploré les propriétés de la plus légère des boules de glu (les boucles fermées du champ chromoélectrique, mentionnées précédemment). Les premiers calculs, effectués par des ordinateurs plus lents que le GF11, étaient trop peu précis pour que l’on identifie clairement des boules de glu. En utilisant 448 des processeurs de GF11 en continu pendant deux ans, nous avons calculé la masse de la boule de glu la plus légère et étudié sa désintégration en d’autres particules plus stables. Les calculs ont montré que cette particule était apparue dans des expériences effectuées au cours des 12 dernières années ; personne ne l’avait reconnue car il n’existait pas de description suffisamment détaillée de ses propriétés. Ainsi nos calculs « découvraient » une particule subatomique.
Malgré ces succès, la chromodynamique quantique doit encore être confirmée directement, sans aucune approximation. À cette fin, on devra utiliser des ordinateurs au moins cent fois plus rapides que le GF11 (ou des algorithmes des centaines de fois plus efficaces que les meilleurs algorithmes actuels). Trois machines de cette envergure sont étudiées à l’Université Columbia, à l’Université de Rome et au Japon. On espère que ces ordinateurs expliqueront également certaines diffusions de particules observées dans les collisionneurs.
La physique théorique expérimentale
Au-delà de la découverte des masses des hadrons et des boules de glu, nos calculs sont le signe d’un changement fondamental de la physique des particules. Alors que les méthodes numériques étaient utilisées dans la plupart des disciplines, papier et crayon restaient les outils des physiciens théoriciens. Nos études numériques, toutefois, se sont imposées parce que les méthodes analytiques avaient échoué et que les ordinateurs étaient devenus assez puissants pour exécuter les algorithmes essentiels.
La simulation numérique sur réseau prend une importance croissante dans un domaine de la physique des particules nommé physique des interactions fortes. La disponibilité de moyens de calcul de puissance, rapidement croissante, permet maintenant une exploration de la chromodynamique quantique dont l’étude avait résisté à des efforts plus analytiques. Des résultats, que je qualifierais de semi-quantitatifs, ont été obtenus, qui valident définitivement à la fois la théorie et cette démarche numérique. Il est possible d’envisager dans un avenir proche, non seulement une reproduction de résultats déjà établis expérimentalement, mais aussi la prédiction de résultats nouveaux. Il faut noter toutefois que la prise en compte précise des degrés de liberté des quarks exigera des puissances de calcul encore supérieures, probablement d’un facteur 100 à 1 000.
Dans certains domaines de la physique, la simulation numérique pourrait-elle, à terme, remplacer l’expérience quand cette dernière est trop difficile ou trop onéreuse ? La simulation numérique ne peut intervenir que dans des domaines où la théorie a déjà des bases suffisamment solides, elle ne peut rien tant que les modèles physiques ne sont pas encore connus. Croire qu’un jour le calcul rendra l’expérience totalement inutile est absurde. Ainsi il est très peu vraisemblable que la simulation numérique joue le moindre rôle dans la solution d’un problème aussi fondamental que celui de la particule de Higgs.
La France est peu présente dans ce domaine d’activité, alors même que nos physiciens (en particulier au Service de physique théorique du CEA-Saclay) ont contribué de façon très importante aux premières études de la chromodynamique sur réseau. Cependant, l’absence de moyens de calcul compétitifs pendant les années 1980, au moment où le sujet s’est développé, a conduit plusieurs équipes à abandonner le domaine. La situation est aujourd’hui meilleure, mais le changement est apparu tardivement.
Jean Zinn-Justin
CEA-Saclay
Cette évolution, du papier à l’ordinateur, a toutefois des conséquences profondes, car, dans les travaux théoriques, sur le papier, chaque étape peut (en principe) être vérifiée ; en étudiant l’enchaînement logique des étapes d’un calcul, on confirme le résultat. En revanche, la physique expérimentale ou le calcul numérique ne donnent pas cette certitude, cette confiance absolue dans les résultats. Dans ces deux cas, des résultats jugés plausibles sont acceptés si suffisamment de tentatives pour les réfuter ont échoué. Nous acceptons le résultat expérimental que toute pierre tombe, et non l’inverse, car personne n’a jamais vu une pierre s’élever spontanément dans l’air ; néanmoins, du strict point de vue logique, il n’est pas certain que les pierres tombent toujours.
Notre travail a été l’analogue d’une recherche infructueuse de pierre qui ne tombe pas. Toutefois, si nous avions pu calculer la masse du proton sur un réseau à maille bien plus petite que celle que nous avons effectivement utilisée du fait de notre puissance de calcul limitée, nous aurions peut-être trouvé une valeur de 2 000 méga-électronvolts (un méga-électronvolt, ou MeV, correspond à 1,78 x 10–30 gramme), en contradiction avec notre valeur extrapolée de 1,67 x 10–27 gramme. Par conséquent, notre prédiction de la masse du proton est testée par la série de nombres entrant dans notre extrapolation, mais elle n’est pas vraiment prouvée.
Nos travaux sont ainsi, ce qui semble une contradiction, de la « physique théorique expérimentale ». Compte tenu de la complexité des théories physiques, du coût des énormes projets expérimentaux et de l’augmentation constante de la puissance des ordinateurs, cette physique théorique expérimentale pourrait, dans certains domaines de la physique, devenir la façon la plus accessible d’étudier les phénomènes naturels.
Quelques références vous sont proposées pour en savoir plus sur les quarks.
- I. Montvay et G. Munster, Quantum fields on a lattice, Cambridge University Press, 1994
- F. Butler, H. Chen, J. Sexton, A. Vaccarino et D. Weingarten, Hadron mass predictions of the valence approximation to lattice QCD, in Physical Review Letters, vol. 70, n° 19, pp. 2849-2852, 10 mai 1993
- M. Creutz, Quarks, gluons and lattices, Cambridge University Press, 1993
- H.J. Rothe, Lattice gauge theories, World Scientific, Singapour, 1992
- D. Weingarten, Lattice quantum chromodynamics, in Particles, Strings and Supernovae, sous la direction de A. Jevicki et C.-I. Tan, World Scientific, Singapour, 1989
- Ta-Pei Cheng et Ling-Fong Li, Gauge theory of elementary particle physics, Oxford University Press, 1984
Une première version de cet article est parue dans la revue Scientific American. Traduction et mise à jour effectuée pour le dossier Pour la Science n°52 La modélisation informatique, exploration du réel, numéro de juillet/septembre 2006.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Donald Weingarten