
Qu’est-ce que Fourier peut nous dire aujourd’hui ?
Une première version de cet article est parue dans la Gazette des Mathématiciens, n°141, en juillet 2014.
En novembre 2012 avait lieu dans l’amphi Henri Cartan à Orsay la remise des diplômes de licence. Pierre Pansu, comme maître de la cérémonie, avait pensé qu’elle devait inclure une conférence générale, et m’avait demandé de l’assurer. Je venais de parler à Nancy, dans le cadre d’un séminaire consacré au rôle des erreurs en mathématiques, des erreurs de Fourier et sur Fourier. C’était un sujet possible. Mais il me fallait savoir où aller, quelle pouvait être l’utilité de la conférence pour les étudiants. J’ai posé la question à Pansu, et la réponse était claire : il faut leur donner confiance.
J’avais donc la matière et le but. Donner confiance devait être le message final. Et cela me plaisait. Je parlerai un peu des erreurs de Fourier et beaucoup des erreurs sur Fourier, et des erreurs sur ses erreurs. Et je donnerai la parole à Fourier quand, dans le « discours préliminaire » à la Théorie analytique de la chaleur, il décrit sa démarche et sa vision optimiste des relations entre la nature, la science, et la raison humaine.
J’ai donc parlé et je n’ai pas conservé de notes. Mais Pierre Pansu est un extraordinaire auditeur et rédacteur, et j’ai trouvé avec surprise le contenu de ma conférence mis par écrit de façon impeccable. La Gazette l’a découvert à son tour, et elle m’a demandé d’en faire un article. La rédaction de Pansu a la vivacité d’un premier jet, j’ai essayé d’en conserver le ton en l’étoffant un peu.
Fourier méconnu
Oui, Fourier a été méconnu. Sa vie est passionnante. La notice nécrologique écrite par Arago après sa mort en 1830 se lit comme un roman : comment un enfant pauvre et orphelin, né en 1768, finit comme secrétaire perpétuel de l’Académie des sciences, à travers l’Ancien régime, la Révolution, l’Empire et la Restauration. Arago parle de son œuvre scientifique majeure, la Théorie analytique de la chaleur. Mais pas un mot sur la méthode introduite par Fourier pour le traitement des équations de la chaleur, les séries et intégrales trigonométriques.
Or, si le nom de Fourier est célèbre aujourd’hui, c’est bien à cause des séries de Fourier, des intégrales de Fourier, de la transformation de Fourier et en particulier de la transformation de Fourier rapide, et de façon générale de l’Analyse de Fourier. D’où vient donc qu’Arago ait occulté toute la partie trigonométrique de l’œuvre de Fourier ?
Arago parle avec éloquence de la vie de Fourier. Élève au Collège militaire d’Auxerre, interdit d’armée par le ministre de la guerre (« Fourier n’étant pas noble ne pourrait entrer dans l’artillerie, quand même il serait un second Newton »), voué à l’église, rompant ses vœux à la faveur de la Révolution pour devenir « instituteur salarié par la nation », élève à l’École normale de l’An III, où il rencontre Monge, Laplace et Lagrange comme professeurs, puis professeur à l’École polytechnique, participant avec Monge à l’expédition d’Égypte, nommé par Bonaparte préfet de l’Isère, destitué, rétabli, destitué de nouveau par Napoléon lors des Cent jours, puis, revenu à Paris comme directeur du bureau des statistiques, membre de l’Académie des sciences et de l’Académie française. En entrant dans le détail de son existence, on ferait un film historique saisissant.

Source gallica.bnf.fr
Arago parle également de son œuvre scientifique et des conditions dans lesquelles elle s’est fait jour : la théorie des équations, sous l’angle de la localisation et du calcul des racines, l’« analyse indéterminée », c’est-à-dire la théorie des inéquations, et surtout la théorie de la propagation de la chaleur. C’est pendant qu’il était préfet de l’Isère, donc isolé de Paris et responsable d’un département difficile, chargé en plus de la présentation de la monumentale « Description de l’Égypte », qu’il a rédigé sa « Théorie analytique de la chaleur ».
Arago ne parle pas des séries trigonométriques. Fourier y attachait de la valeur ; c’était l’« analyse spéciale » qui lui permettait le traitement des équations de la chaleur. Mais il a dû se battre pour les faire admettre. Lagrange, le plus respecté des mathématiciens de l’époque, y était complètement opposé. Il s’était intéressé à la question 50 ans auparavant, lors de la controverse sur les cordes vibrantes qui avait opposé D’Alembert, Euler et Daniel Bernoulli. Ce dernier décomposait des fonctions en séries trigonométriques. Tous les autres, Lagrange compris, avaient condamné cette approche. Or, curieusement, j’en dirai un mot, elle était très bien adaptée aux problèmes considérés par Fourier.
Fourier, de Grenoble, envoya à l’Institut une première version en 1807. Pas de réaction. Fourier, ayant eu vent des réticences, tenta par lettres à Laplace et à Lagrange de montrer le bien-fondé de sa méthode. Le sujet de la propagation de la chaleur fut alors proposé pour un prix en 1811. Fourier concourut, il obtint le prix, mais les considérants, tout en appréciant la mise en équations, furent réticents sur leur traitement, qui « laisse encore quelque chose à désirer, soit relativement à la généralité, soit même du côté de la rigueur ».
Arago avait alors 25 ans et il était déjà membre de l’Institut, comme astronome. Il enregistra ces réserves, il n’était donc pas question, ni alors, ni plus tard, de parler de séries trigonométriques à propos de Fourier.
Fourier non fiable du côté de la rigueur, cette appréciation a perduré. Fourier eut beau entrer à l’Académie des sciences et en devenir secrétaire perpétuel, publier intégralement sa Théorie analytique de la chaleur et revenir au sujet à plusieurs reprises, se faire reconnaître comme un maître par les jeunes mathématiciens de l’époque, Dirichlet, Sturm, Navier, la suspicion resta qu’il n’était pas un vrai mathématicien. Il fallut la caution de Riemann dans sa thèse sur les séries trigonométriques de 1854 pour reconnaître qu’avec Fourier « une nouvelle ère s’ouvrit pour le développement de cette partie des mathématiques ». Mais cette thèse fut publiée tardivement, en 1867, elle fut traduite en français en 1873, et sa partie historique, excellente à tous égards, n’eut pas le succès de lecture qu’elle mérite, en France du moins.
En 1862, d’exil à Guernesey, Victor Hugo publia « Les Misérables ». Le chapitre sur l’année 1817 commence par une série de flashes. L’un d’eux concerne Fourier : « Il y avait à l’Académie des sciences un Fourier célèbre que la postérité a oublié et dans je ne sais quel grenier un Fourier obscur dont la postérité se souviendra ». Hugo connaissait bien Arago, il ne se trompe pas sur la date, Joseph Fourier est entré à l’Académie des sciences en 1817, il se trompe sur le jugement de la postérité, mais à peine. Dans l’édition d’Encyclopedia universalis que j’ai chez moi, et qui date de 1974, il y a un article sur l’utopiste Charles Fourier, pas d’article sur Joseph Fourier. Il y a à Paris une rue Charles Fourier, pas de rue Joseph Fourier. Il n’y a pas d’édition complète des œuvres de Fourier. Quand Darboux a édité une partie de son œuvre, il a laissé de côté ce que Fourier appelait l’analyse indéterminée et qui introduisait ce que nous appelons aujourd’hui l’analyse convexe et la programmation linéaire. Darboux explique que Fourier attribuait à ce sujet une importance « exagérée ». On découvre aujourd’hui que Fourier a expliqué l’effet de serre, c’était resté ignoré quoique publié.
Cette méconnaissance de Fourier est maintenant datée. Elle ne s’est maintenue en France qu’à la faveur d’un divorce entre mathématiques et physique qui est aujourd’hui complètement résorbé. L’une des plus grandes universités françaises, à Grenoble naturellement, porte le nom de Joseph Fourier. Le livre de Dhombres, mathématicien, et Robert, physicien, « Fourier, créateur de la physique mathématique », qui date de 1998, fait excellemment le point sur l’époque, la vie et l’œuvre de Fourier. L’année 2005, qui fut l’année internationale de la physique, fut l’occasion pour l’Académie des sciences d’honorer Fourier comme physicien et de constater, sous ma plume, « le retour de Fourier ». Il est clair, et j’en suis un exemple, que ceux qui s’intéressent à lire Fourier ne le lisent pas aujourd’hui comme ils le lisaient autrefois. Autrefois j’aimais à repérer les bizarreries et ce que je prenais pour des erreurs, aujourd’hui je suis admiratif devant tout ce qu’il écrit. La plus grave erreur est de méconnaître Fourier. J’ai indiqué deux sources : la méfiance devant les séries trigonométriques, et le divorce entre physique et mathématiques. On va regarder de plus près la première.
Fourier et les séries trigonométriques
Le point de départ est un problème d’équilibre thermique. L’équation de Fourier, l’équation de propagation de la chaleur à l’intérieur d’un solide, quand on la débarrasse des coefficients qui en font l’importance en physique, s’écrit :
\[\frac{\delta u}{\delta t}=\Delta u.\]
L’établir occupe toute la première partie du mémoire de Fourier. La fonction u = u(x, y, z, t) est la température en (x, y, z) au temps t. Prenons une barre dont la base est une bande horizontale et dont les parois verticales sont des demi-plans :
on l’écrit
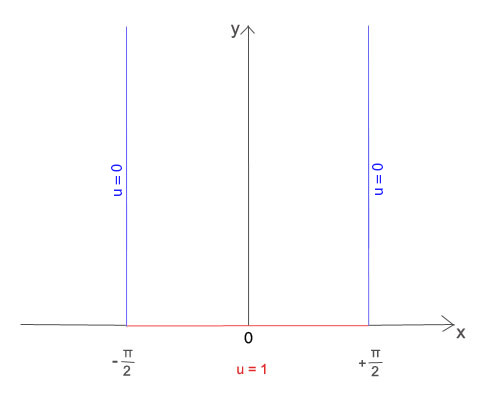
Si l’on omet la seconde donnée, on a pour solution
(1) u = a cos x · exp(−y) + b cos 3x · exp(−3y) + ···
Fourier a l’idée surprenante de décomposer la fonction constante 1 sur l’intervalle (−π/2, π/2) comme somme d’une série
(2) 1 = a cos x + b cos 3x + ···
et il en déduit l’expression de la solution sous la forme (1).
Ses contemporains ont eu du mal à digérer cette idée. Il faut dire que Fourier écrit comme il pense : il écrit la formule (2) et montre comment on peut calculer les coefficients a, b, etc. En reportant les valeurs de ces coefficients dans (1), il obtient une série rapidement convergente quand on fixe y > 0. C’est ce qui pour lui justifie la méthode. Quant à la démonstration de la validité de (2), il l’établit quelques pages plus loin, et le lecteur hâtif que j’étais autrefois ne la découvre pas d’emblée. La suite du mémoire, sur 50 pages, consiste à exprimer toute une série d’exemples de fonctions comme sommes de séries trigonométriques. À la fin, il énonce que toute fonction est développable en série trigonométrique sur un intervalle convenable, avec des coefficients donnés par des intégrales.
Il ne donne la démonstration que dans quelques cas, mais ces cas sont typiques et la méthode est générale : elle consiste à écrire les sommes partielles comme convolution de la fonction et de ce que nous appelons aujourd’hui le noyau de Dirichlet. C’est exactement la méthode par laquelle Dirichlet, en 1829, établira le premier théorème général sur la convergence des séries de Fourier. Et sur les cas particuliers, la démonstration de Fourier est impeccable.
Cependant, c’est sur un tel cas particulier que Lagrange a cru réfuter le résultat de Fourier. Cela apparaît sur une feuille dans les manuscrits de Lagrange conservés à la Bibliothèque de l’Institut, et j’ai découvert cette feuille d’après les indications que donne Riemann, qui lui-même tenait son information de Dirichlet. Curieusement, cette feuille est suivie d’une autre feuille, de la main de Fourier, qui réfute la réfutation. Lagrange part de l’expression que donne Fourier de la fonction f (x) = x/2 comme somme de sinus d’arcs multiples sur l’intervalle (0, π), il fait une série de calculs, et la contradiction à laquelle il aboutit consiste en fait à dire que l’expression n’est pas valable quand x = π. Fourier examine les calculs de Lagrange en détail, précise que l’expression est valable sur l’intervalle ouvert (−π, π) et qu’on ne doit pas la prolonger au-delà et il conclut qu’« en général on ne peut pas séparer l’usage d’une équation de ce genre de la considération des limites entre lesquelles les valeurs de la variable doivent être considérées ».
Préciser l’ensemble de définition est une idée forte de Fourier. Le terme d’intervalle ouvert lui est bien postérieur, mais il précise les inégalités strictes que la variable doit respecter. D’ailleurs c’est à lui que l’on doit d’écrire l’intégrale définie comme nous le faisons, en précisant les bornes. Fourier non rigoureux ? C’est à voir.
Par exemple, Darboux relève une absurdité dans une formule de Fourier. C’est page 234 au chapitre III des Œuvres, une façon concentrée d’écrire que la fonction est somme de sa série de Fourier :
\[F(x)=\frac{1}{\pi}\int F(\alpha) \mathrm{d}\alpha \left ( \frac{1}{2} + \sum \cos i(x-\alpha) \right ) \]
et Darboux observe que la parenthèse n’a aucune signification. Or voici ce qu’écrit Fourier : « L’expression 1/2 + ∑ cos i (x − α) représente une fonction de x et de α telle que, si on la multiplie par une fonction quelconque F(α) et si, après avoir écrit dα, on intègre entre les limites α = −π et α = π, on aura changé la fonction F(α) en une pareille fonction de x, multipliée par la demi-circonférence. On verra par la suite quelle est la nature de ces quantités, telles que 1/2 + ∑ cos i (x − α), qui jouissent de la propriété que l’on vient d’énoncer. »
Dans la suite du mémoire en effet Fourier utilise librement ce que nous appelons aujourd’hui les séries de Fourier et intégrales de Fourier de la mesure de Dirac et de ses dérivées. Abus d’écriture en son temps, mais vision prophétique d’autre part.
À nos yeux ce qui reste comme erreur de Fourier est d’avoir écrit que le couplage des formules
et
Or, Dirichlet l’a d’abord observé, comme les coefficients de la série sont donnés par des intégrales, il faut que la fonction F soit intégrable. Cette remarque porte très loin. Elle établit le lien entre séries de Fourier et théorie de l’intégrale. Pour Dirichlet, il fallait que la fonction soit continue sur un intervalle. Puis Riemann a défini l’intégrale et donné son critère d’intégrabilité à l’occasion de sa thèse sur les séries trigonométriques. Puis Lebesgue a donné comme première suite à son intégrale son cours Peccot sur les séries trigonométriques. Puis Denjoy a développé sa totalisation dans les quatre volumes de ses « leçons sur le calcul des coefficients d’une série trigonométrique ». Puis Wiener a tiré la série de Fourier du mouvement brownien de ce qu’on appelle l’intégrale de Wiener. Puis Schwartz, dans son premier article sur les distributions, indique dès le titre l’application à la transformation de Fourier. Et dans ces dernières années le « compressed sensing » de Candès et Donoho commence par la reconstitution d’un signal à partir d’un petit nombre de ses coefficients de Fourier. Il y a plusieurs notions d’intégrale, et celle de série de Fourier dépend de la notion choisie : il y aura donc les séries de Fourier-Riemann, de Fourier-Lebesgue, de Fourier-Denjoy etc, mais dans aucun cas on ne pourra prendre pour F une fonction arbitraire.
Quant à la convergence de la série de Fourier, c’est depuis Fourier l’objet de recherches qui ne sont pas achevées. Dirichlet a donné en 1829 un premier théorème général, et il espérait revenir au sujet en démontrant la convergence dès que F est une fonction continue. Un contre-exemple est venu avec Paul du Bois-Reymond en 1873. Jusqu’en 1966 on pouvait se demander s’il existait une fonction continue dont la série de Fourier diverge partout. En effet, il existe une série de Fourier-Lebesgue qui diverge partout (Kolmogorov 1926). Alors est venu le théorème de Carleson disant que, si F est de carré intégrable, la série de Fourier de F converge presque partout. Un problème non résolu est l’estimation de l’ordre de grandeur des sommes partielles d’une série de Fourier-Lebesgue presque partout.
Le plus important a été de changer le point de vue. Au lieu de la convergence ponctuelle, la convergence dans un espace fonctionnel s’impose à bien des titres. D’autre part, au lieu de s’attacher uniquement aux sommes partielles, on peut considérer des procédés de sommation des séries ; c’est le sujet introduit par Fejér en 1900.
Riemann insiste sur l’importance du couplage des deux formules F = ∑ et c = ∫. Fourier les a présentées comme ayant une valeur universelle, et il avait tort si on les traite comme un théorème. Mais il avait raison si on les considère comme un programme. Donner des conditions pour leur validité, et des extensions dans des cadres plus étendus, cela a été un ressort constant dans l’analyse de Fourier, et au-delà.
Quelques citations de Fourier
Les citations qui suivent sont extraites du Discours préliminaire à la Théorie analytique de la chaleur.
Il s’agit d’abord de l’intérêt des recherches sur la propagation de la chaleur.
… Ces recherches intéressent les sciences physiques et l’économie civile, … les progrès des arts, … le système du monde … les grands phénomènes qui s’accomplissent près de la surface du globe terrestre …
Suivent deux pages d’explications, puis une série de questions, un aperçu de la théorie, et une réflexion d’ensemble sur les sources et la portée de l’analyse mathématique.
… telles sont les questions principales que j’ai résolues … Les principes de cette théorie sont déduits, comme ceux de la mécanique rationnelle, d’un très petit nombre de faits primordiaux … Les équations différentielles de la propagation de la chaleur expriment les conditions les plus générales, et ramènent les questions physiques à des problèmes d’analyse pure, ce qui est proprement l’objet de la théorie …
Après avoir établi ces équations différentielles, il fallait obtenir les intégrales … Cette recherche difficile exigeait une analyse spéciale, fondée sur des théorèmes nouveaux. La méthode qui en dérive ne laisse rien de vague et d’indéterminé dans les solutions ; elle les conduit jusqu’aux dernières applications numériques, condition nécessaire de toute recherche, et sans laquelle on n’arriverait qu’à des transformations inutiles.
L’étude approfondie de la nature est la source la plus féconde des découvertes mathématiques. L’analyse mathématique est aussi étendue que la nature elle-même … Elle rapproche les phénomènes les plus divers, et découvre les analogies secrètes qui les unissent. Elle semble être une faculté de la raison humaine destinée à suppléer à la brièveté de la vie et à l’imperfection des sens.
J’interromps ici les citations du Discours préliminaire. Elles peuvent être mises en regard d’une belle lettre du jeune Jacobi à Legendre, son ainé de cinquante ans, juste après la mort de Fourier. Jacobi apprécie beaucoup Fourier, mais réagit à l’utilisation par Poisson d’une phrase de Fourier regrettant qu’Abel et lui, Jacobi, ne se soient pas occupés du mouvement de la chaleur.
… M. Fourier avait l’opinion que le but principal des mathématiques était l’utilité publique et l’explication des phénomènes naturels. Mais un philosophe comme lui aurait dû savoir que le but unique de la science, c’est l’honneur de l’esprit humain, et que sous ce rapport une question de nombres vaut autant qu’une question de système du monde.
Quand j’étais jeune, et c’est encore le cas aujourd’hui parmi les jeunes, « l’honneur de l’esprit humain » sonnait plus glorieux que « l’étude approfondie de la nature ». Cependant la philosophie de Fourier me paraît plus proche que jamais de l’évolution actuelle des mathématiques et de leur portée, qualifiée parfois de « déraisonnable », dans les sciences de la nature. Voici d’ailleurs ce que dit Fourier dans un manuscrit inédit (BN 22501 page 10) :
Les progrès que la raison a faits dans les derniers siècles ne permettent plus de comparer cette époque à aucune de celles dont l’Histoire nous a laissé le souvenir. Nous ne pouvons pas juger par l’Histoire de l’influence que les sciences auront sur le bonheur des hommes et sur l’état des sociétés.
Fourier a été mêlé au tourbillon de la vie publique en France à son époque. La confiance dans la raison a été sa boussole. À l’heure actuelle, il n’est pas certain que tout le monde fasse confiance à la raison. Les sciences et les mathématiques en particulier, qui ont fait des progrès bouleversants depuis Fourier, ne sont pas associées spontanément au bonheur des hommes et aux progrès des sociétés. C’est plutôt la défiance à leur égard qui s’exprime le plus souvent, au point parfois de les tenir responsables des désordres économiques et financiers dans lesquels nos sociétés sont engluées. Personnellement, j’ai assez confiance dans les ressources de l’humanité pour se sortir des ornières et retrouver le chemin du bonheur et du progrès. Le chemin n’est pas tracé, il est à découvrir, et c’est un défi pour la raison humaine. Nous avons tous à y œuvrer, et les jeunes qui s’engagent vers les mathématiques y ont une part originale et essentielle.
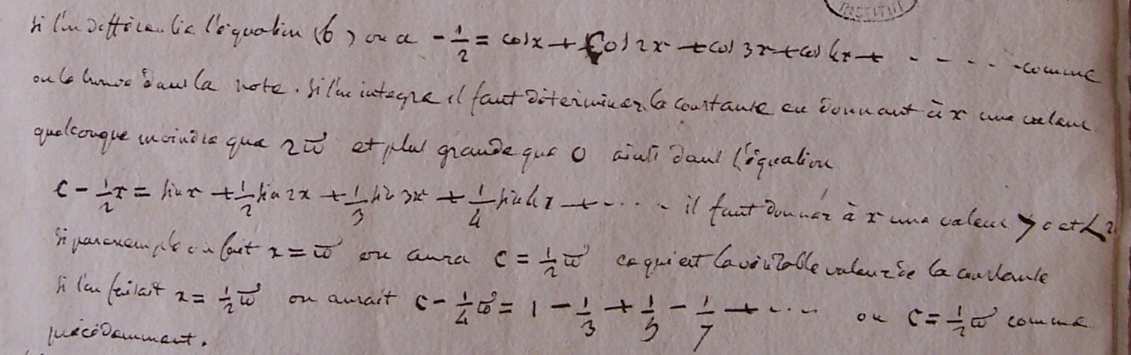
Extrait de la page de Fourier dans les manuscrits de Lagrange. Reproduit avec l’aimable autorisation de la Bibliothèque de l’Institut.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Pierre Kahane