Reconnaître un animal : notre cerveau est plus rapide que nous !

Alors, comment notre cerveau catégorise-t-il des objets ? Le mieux, c’est que vous veniez faire l’expérience vous-même.

Venez : nous allons faire un test

Allons au Centre de Recherche Cerveau et Cognition, ce laboratoire de l’université Paul Sabatier à Toulouse où le professeur Simon Thorpe nous accueille volontiers.

Dispositif de mesure de l’électroencéphalogramme.

Asseyez-vous, ici, face à ce grand écran ; la jeune femme qui vous sourit sur votre droite est le docteur Holle Kirchner, et la petite caméra  qu’elle ajuste devant vous va permettre de filmer le mouvement de vos yeux, pour détecter à quel instant votre cerveau va réagir à l’image qui va vous être présentée. Les inoffensives électrodes qui viennent d’être posées sur votre crâne sont les mêmes que celles qui ont permis de vérifier que vous ne souffriez pas d’épilepsie il y a quelques années : elles mesurent l’électroencéphalogramme (EEG), ces courants générés par votre cerveau lors du déroulement de votre pensée.

Ne perdons pas de temps : une image vient d’apparaître sur l’écran pendant 10 millisecondes. Oui, ce « flash » lumineux était une vraie photo, une scène naturelle. D’ailleurs, nous avons une question : « Y avait-il un animal présent dans la scène ? » Vous n’avez pas eu le temps de voir ? Mmm. Je crois qu’il vous faut tout de même fournir une réponse. S’il vous plaît, appuyez sur le bouton vert pour signifier « oui » et le rouge pour « non ». Après tout,  vous avez seulement une chance sur deux de vous tromper ! Il vous est même demandé de répondre le plus vite possible en appuyant sur l’un des deux boutons.

Écoutez, je ne voudrais pas vous vexer, mais, avant vous, un compagnon du petit macaque que vous vous êtes amusé à venir saluer en arrivant au labo a déjà réalisé cette expérience des heures durant avec le professeur Michèle Fabre. Lui s’est visiblement passionné pour ce jeu visuel sensori-moteur qui semble vous rebuter.

Alors, on y va. Oui, il y aura plusieurs dizaines de flashes, et vous de presser le bouton vert ou rouge sans relâche, même si,  d’évidence,  tout cela se passe un peu trop vite pour que vous ne sembliez faire autre chose qu’un jeu de hasard.

Alors ? Ce n’était pas si terrible, finalement ? Comme quoi. Maintenant, venez dans la pièce à côté. Holle a lancé les logiciels qui analysent vos données. Le jeune ingénieur devant l’ordinateur est Jong-Mo Allegraud. Avec Simon, il participe à une jeune pousse technologique, SpikeNet, qui valorise ce résultat stupéfiant que vous êtes à une seconde de découvrir.

Sur ces images, la présence d’un animal est bien détectée ;	sur celles-ci, l’absence d’animal est bien détectée ;	sur ces dernières, la présence d’un animal est mal détectée.

À votre avis, quel a été votre nombre de réponses exactes ? Une sur deux ? Un peu plus ?

Regardez, mais regardez donc : 99% de réponses exactes !!! Oui, c’est bien cela qui s’est passé : pendant que vous pressiez au mieux ces boutons, votre cerveau catégorisait les images sans aucune hésitation ! Pire : il le faisait à une vitesse presque incroyable : moins d’un dixième de seconde ! Regardez le tracé de votre électroencéphalogramme : environ 100 millisecondes après que l’image est apparue, les aires de votre cerveau où se réalise la reconnaissance d’objets avaient déjà rendu leur verdict.

Que dites-vous ? Le singe ? Ah oui, le petit primate a réalisé cette expérience avec le même succès que vous ! Il a même été un peu plus rapide, humilité oblige, et… tout aussi précis. Il faut dire que ça se comprend aisément : les animaux qui ont été amenés à survivre à leurs prédateurs ou à profiter de leurs proies sont sûrement ceux dont le cerveau était doté du mécanisme de reconnaissance le plus efficace possible.

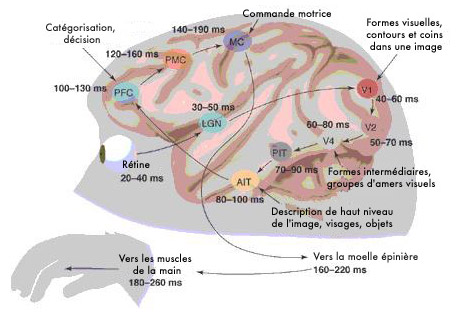
Schéma de l’information visuomotrice dans le cerveau d’un singe lors de la catégorisation rapide.
Image : Simon Thorpe et Michèle Fabre-Thorpe.

Maintenant, si Simon Thorpe est connu internationalement pour un ensemble de travaux extrêmement détaillés sur ces mécanismes de catégorisation rapide, c’est qu’il a proposé un modèle qui bouleverse complètement les idées admises sur le sujet. Il a remarqué qu’en 100 millisecondes,

1. sachant que chaque neurone a besoin d’environ 10 millisecondes pour traiter les signaux qui arrivent,
2. et sachant qu’il y a justement entre la rétine et le centre cérébral qui catégorise les objets, environ 10 couches de neurones,

la seule chose, le seul calcul que le cerveau a été en mesure de faire, c’est de propager en vrac à toute vitesse une énorme quantité de valeurs correspondant à chaque élément de l’image à cette zone du cerveau, qui a dû en une seule étape de traitement classer ce gigantesque vecteur de valeurs dans la catégorie « animal » ou « pas d’animal ». Simon remarque aussi deux autres choses :

1. seules les valeurs qui ont été calculées le plus vite sont retenues, car elles correspondaient aux aspects les plus évidents, les plus saillants, les autres arrivent trop tard de toute façon ;
2. d’une valeur à l’autre, dans le cerveau, il y a forcément une grande marge, car dans un calcul aussi rapide, un petit nombre seulement de valeurs différentes peuvent être considérées.

En effet, l’information dans les neurones est codée sous forme de trains d’impulsions : des « spikes ». C’est un codage temporel, où les valeurs les plus élevées sont émises d’abord. Et un tel spike dure environ 1 milliseconde. Dans une fenêtre temporelle de 10 millisecondes, seules 10 valeurs différentes peuvent être considérées. Ce mécanisme a aussi été simulé sur ordinateur, ce qui est à l’origine de la jeune pousse technologique que nous avons citée.

Sur cette base, le cerveau s’entraîne depuis quelques millions d’années, au fur et à mesure de l’évolution des espèces. Mais les scientifiques actuels se demandent bien par quel mécanisme mathématique on peut attacher à un paquet de valeurs en vrac une étiquette aussi sophistiquée.

Pour avancer, voyageons de Toulouse à Nancy. Là-bas, au LORIA, il y a un jeune informaticien, Yann Guermeur, qui sans le savoir encore, détient la clé de ce mécanisme que Simon Thorpe étudie quotidiennement.

Les machines à vecteurs supports : un outil algorithmique que les ordinateurs utilisent avec succès

Yann prend un air désolé, ce qu’il a à nous expliquer est un peu compliqué. Le livre original de Vapnik qui en 1995 développait cette théorie est basé sur une trentaine de théorèmes, et près de 300 pages de démonstration. Depuis, une petit centaine de mathématiciens de par le monde ont complété, décuplé, corrigé aussi d’ailleurs, ces milliers de lignes de calculs. Des calculs qui permettent de mettre à la disposition des ordinateurs la méthode actuellement la plus performante de classification de données : les machines à vecteurs supports.

Yann Guermeur est un des rares spécialistes qui maîtrise cette théorie à laquelle il a largement contribué.

Une méthode, compliquée certes, mais finalement très simple à utiliser : prenons – par exemple – une bonne centaine de petites séquences vidéo. Dans certaines d’entre elles, la personne filmée marche normalement (« walk » diront les anglo-saxons), dans d’autres elle marche « militairement » (les anglo-saxons diront alors « march »). C’est presque la même chose, mais un cerveau humain fait sans conteste la différence, vous pouvez le vérifier dans les images ci-dessous. En utilisant des machines à vecteurs supports implémentées sous forme de réseaux de neurones biologiquement plausibles, l’ordinateur a su lui aussi catégoriser ce stimulus compliqué.

Exemples de séquences de « walk » et de « march ». Image : Martin Giese et Tomaso Poggio.

Pour cela, dans une première phase d’apprentissage supervisé, enregistrons dans la mémoire de l’ordinateur des exemples de « walk », « march », etc., en lui indiquant ce qui est quoi. Comme dans le cerveau, l’ordinateur va très rapidement calculer, à partir de ces séquences vidéo, des indices liés aux contours et aux mouvements d’une image à l’autre, et fabriquer pour chaque séquence un vecteur de valeurs en vrac, qui représente les données en entrée. Mais comme Simon Thorpe l’avait remarqué pour le cerveau, dans ce calcul, seules vont être prises en compte :

• les valeurs les plus saillantes, disons environ un millier parmi les quelques millions de valeurs issues de la séquence vidéo,
• en se limitant à des valeurs séparées par une marge suffisante.

Eh bien imaginez, nous propose Yann Guermeur, que chaque séquence vidéo est un point dans un espace de très grande dimension, où chaque valeur correspond à un des paramètres qui ont été retenus précédemment.

Distinguer une façon de marcher telle que « walk » revient alors à trouver une frontière telle que tous les points qui correspondent à « walk » sont du même côté de la frontière. Pour illustrer ce point, dans la petite applet Java ci-dessous, on a symbolisé chaque façon de marcher par un point de couleur différente. Appuyez sur « Calcul » pour afficher la frontière trouvée par le classificateur.

Sélectionnez un classificateur, puis cliquez sur « Calcul » pour afficher la frontière trouvée.
« Raw » tient compte de la distance à chaque point, « YG » s’inspire de la méthode de Yann Guermeur en s’appuyant sur un choix de prototypes, « YG-polynomial » est une variante plus complexe du précédent.

Nous vous proposons deux exemples à tester. Pour observer le fonctionnement de ces classificateurs sur d’autres exemples, vous pouvez effacer tous les points en cliquant sur « Effacer » puis choisir dans le nuancier une couleur, placer de nouveaux points, choisir ensuite une autre couleur, placer d’autres points, etc., et lancer le calcul sur l’exemple que vous aurez ainsi défini.

Pour séparer les points en fonction de leur couleur, le calcul a dessiné cette frontière en tenant compte de la distance à chaque point. Mais ce n’est pas la meilleure façon de faire. Un meilleur calcul va, parmi tous ces exemples, ne garder que les plus utiles, éventuellement en les modifiant. Ils seront les prototypes qui serviront de support pour séparer les différentes catégories. Et cette frontière est calculée sur une base très simple : maximiser la marge par rapport aux prototypes, pour éviter autant que possible de se tromper dans le classement.

Pour visualiser cette nouvelle méthode de classification, à la place de « Raw » choisissez « YG » (les initiales de Yann Guermeur, car nous avons implémenté là une variante de sa méthode, en utilisant des mécanismes biologiquement plausibles basés sur les modèle de Simon Thorpe), et relancez « Calcul » : la frontière qui apparaît est bien plus simple. Elle effectue la classification, mais en recherchant un modèle de complexité minimale.

À partir de l’une ou l’autre de ces frontières, quand une nouvelle séquence va être présentée, il suffira de regarder de quel côté de la frontière elle se trouve dans cet espace et « instantanément » il sera possible de reconnaître à quelle catégorie elle appartient. C’est là toute la puissance du mécanisme, qui explique sa redoutable efficacité : il s’applique à la reconnaissance de protéines, à la reconnaissance d’un alphabet de sourds-muets, etc.