S’aider des graphes pour élaborer une notice de montage

La version originale de cet article a été publiée sur The Conversation.

Une fois les matériaux et les outils en main, il ne vous reste plus qu’à démarrer les travaux. Certes, mais par où commencer ? Dans quel ordre mener les nombreuses opérations qui permettront de métamorphoser ce tas de planches, tuiles, vitres, serrures, isolants et câbles électriques en une magnifique cabane de jardin qui fera votre fierté ?

Réaliser un projet en n étapes

Prenons un peu de hauteur de vue, et examinons la situation de manière plus abstraite. Il s’agit clairement de réaliser un projet, composé de tâches, que l’on notera T1, T2… Tn : monter les murs, creuser des fondations, poser des tuiles, etc. Avec, toutefois, une particularité. Il n’y a qu’une seule ressource pour exécuter toutes ces tâches : vous.

Avant de débuter, il convient de savoir dans quel ordre exécuter les n tâches. Tous les ordres ne se valent pas : poser des tuiles alors que les murs ne sont pas édifiés serait absurde. Il faut respecter des contraintes. Quelles sont-elles ?

On distingue principalement les contraintes de « précédence ». Une telle contrainte, écrite sous la forme T’->T, indique que la tâche T ne peut pas débuter tant que la tâche T’ n’a pas été achevée (c’est le cas par exemple si la tâche T a besoin du résultat de celle de T’ pour pouvoir démarrer). Attention, il est possible que T dépende de plusieurs tâches. Dans ce cas, T ne pourra commencer que lorsque chaque tâche X avec X->T aura été exécutée, soit immédiatement après, soit plus tard, mais en tout cas pas avant.

Un ordre d’exécution valide

L’objectif est d’élaborer un ordre d’exécution valide de toutes les tâches respectant toutes les contraintes de « précédence ».

Première question à se poser : est-il toujours possible de trouver un tel ordre valide ? La réponse est non s’il y a des contraintes circulaires. Imaginons que le système contienne les contraintes A->B, B->C, C->A. Traduisons-les en langage courant : la tâche A ne peut se faire qu’une fois la C bouclée, laquelle ne peut être exécutée sans que la B soit achevée, mais cette tache B elle-même n’est réalisable qu’une fois la A finie. En résumé : pour débuter la tâche A, il faut attendre qu’elle soit terminée ! Bien entendu, c’est impossible. Nous supposerons donc dans la suite qu’il n’y a pas ce type de circularité dans les contraintes.

Ceci étant posé, existe-t-il toujours au moins une solution ? D’autres conditions pourraient constituer un blocage. Ce n’est toutefois pas le cas ici. Lorsqu’il n’y a pas de circularité dans les contraintes, il y a une solution – voire plusieurs. Autre bonne nouvelle : plusieurs algorithmes efficaces sont connus pour les trouver. Nous allons nous contenter d’en décrire un.

Des tâches et des contraintes

Considérons le système suivant de contraintes où les tâches sont simplement représentées par des nombres entiers allant de 1 à 9.

1->8, 3->1, 3->2, 3->5, 4->2, 4->3, 5->6, 5->8, 7->5, 9->5.

À partir des tâches et contraintes, il est possible de construire un graphe orienté qui les représente. Une contrainte X->Y est dessinée sous la forme d’une flèche orientée, que l’on appelle arc du graphe, du sommet X vers le sommet Y. Voici celui correspondant aux contraintes précédentes.

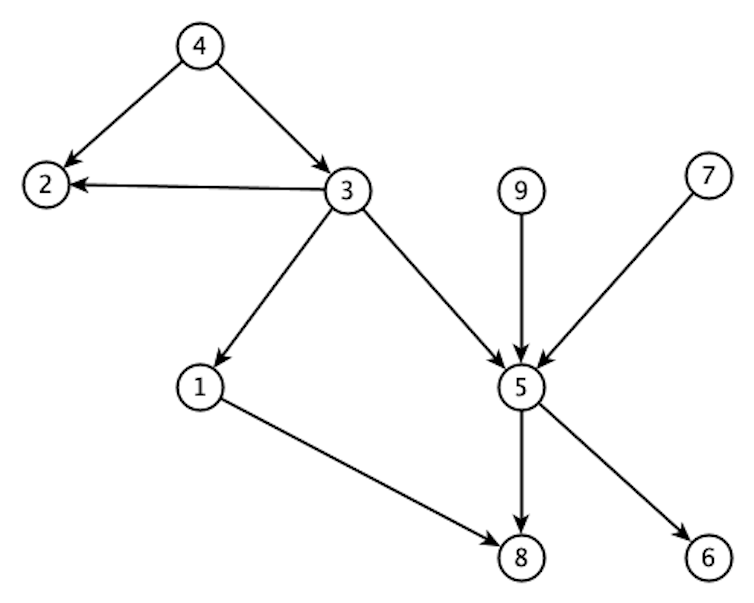
DAG Tri Topologique. © Christian Laforest

Comment trouver au moins un ordre valide ? Comment réaliser cette opération automatiquement ?

Ce dernier point est du ressort de l’informatique. Il s’agit de proposer un algorithme prenant comme entrée un graphe des contraintes (sans circuit) et donnant comme résultat un ordre valide.

L’aide des algorithmes

Notons d’abord que tous les ordres ne sont pas valides. Par exemple 1, 2, 3, 4, 5, 6, 7, 8, 9 ne l’est pas : en effet, la tâche 1 ne peut pas être la première tâche exécutée, étant donné qu’elle requiert que la tâche 3 ait déjà été accomplie. Voyons donc quelle tâche peut être exécutée en premier. Ce ne peut être la 1, comme nous venons de le voir. On peut aussi éliminer les tâches 2, 3, 5, 6 et 8, elles aussi associées à des contraintes. Restent les tâches 4, 7 ou 9.

Choisissons de commencer par la 4. On libère alors les contraintes 4->2 et 4->3, et les arcs correspondants disparaissent. Du coup, les tâches pouvant suivre 4 sont à la fois 7 et 9, mais aussi la 3, qui n’avait pas d’autre impératif pour être réalisable que l’exécution de la tâche 4 (dans le graphe obtenu par la suppression de 4, la tâche 3 se retrouve sans arc entrant). Il est alors possible de continuer ainsi jusqu’à ce que toutes les tâches aient été traitées. L’algorithme suivant, décrit de manière simplifiée, reprend ces idées et construit un ordre valide sous la forme d’une liste L des tâches.

• Au départ, la liste L est vide.

• Tant que le graphe contient au moins un sommet faire :

• Choisir un sommet u n’ayant aucun arc entrant.

• Ajouter u à la fin de la liste L.

• Supprimer u de G, ainsi que tous ses arcs.

Retourner la liste L comme résultat final.

Appliquée sur l’exemple précédent, cette méthode permet de trouver la solution 4, 9, 3, 2, 7, 5, 6, 1, 8 ou la solution 9, 4, 3, 7, 2, 5, 1, 8, 6 (ou d’autres) en fonction du choix réalisé parmi les tâches candidates à chaque étape.

Prenons la première solution, et re-dessinons le graphe dans l’ordre produit.

DAG Tri Topologique. © Christian Laforest

Les arcs sont tous orientés de la gauche vers la droite : c’est bien une solution valide, appelée ordre topologique.

L’algorithme présenté ici est particulièrement simple à « dérouler à la main » sur un petit graphe. Il en existe néanmoins un autre, très élégant mais moins simple à comprendre, basé sur un parcours en profondeur du graphe.

De très nombreuses variantes du problème initial sont possibles (nombre de ressources d’exécutions plus grand, tâches demandant plusieurs ressources simultanées pour être exécutées, etc.) mais toutes ne sont pas aussi faciles à résoudre. Pour certaines, aucune méthode efficace n’est connue (problèmes NP-complets).

Quoi qu’il en soit, vous n’avez maintenant plus aucune excuse pour ne pas démarrer votre projet de cabane au fond du jardin !