Un exemple de modélisation : le condensat de Bose-Einstein
Imaginez qu’un matin, en effectuant le geste rituel de mélanger votre café avec une petite cuillère, le liquide refuse obstinément de tourner. Hautement improbable ? Pas tout à fait si le café, fluide de son état (comme tous les liquides et les gaz, il obéit aux lois fondamentales de la mécanique des fluides), est remplacé par un superfluide. Dans ce dernier, l’absence de toute forme de frottement entre molécules fait que la mise en rotation s’effectue suivant un scénario qui défie notre intuition (voir les deux photographies ci-dessous) : pour des rotations faibles, l’absence de forces de viscosité fait que le superfluide reste immobile ; pour des rotations importantes, des tourbillons quantifiés (ou vortex) apparaissent. Ces tourbillons sont des zones dépourvues d’atomes, autour desquelles le superfluide tourne localement. En augmentant progressivement la vitesse de rotation, de plus en plus de tourbillons apparaissent, s’organisant dans un réseau triangulaire qui porte le nom d’Alexei Abrikosov (prix Nobel de physique en 2003).

Quand un superfluide remplace un fluide. © Ionut Danaila.
Lorsqu’un liquide classique est mis en rotation (tasse à café, à gauche), les forces de frottement impriment une rotation en bloc. Le superfluide (simulé numériquement, à droite), se met en rotation par nucléation de tourbillons quantiques, qui apparaissent comme des petits trous désertés par les atomes du fluide (cercles noirs).
Comment obtenir un « café » superfluide ?
L’idée est de réduire l’agitation moléculaire, et, par la même occasion, le frottement entre molécules, en réduisant drastiquement la température du fluide. Comme l’eau reste figée sous forme de glace solide en dessous de 0 °C, il va falloir la remplacer par un gaz pour atteindre des températures inférieures et garder le même état fluide de la matière. On sait que la température est une mesure de l’agitation atomique (ou moléculaire) d’un gaz et que le « zéro absolu » ou 0 kelvin (équivalent à – 273,15 °C) correspond au gel de toute agitation moléculaire. Ce qui est surprenant, c’est le fait qu’il est possible de discipliner le mouvement, habituellement désordonné, des atomes quand la température descend à quelques milliardièmes de degré au-dessus du zéro absolu, soit quelques nanokelvins (même l’espace interstellaire est maintenu par le rayonnement cosmologique à une température plus confortable d’environ 3 kelvins).
Cette discipline s’impose naturellement par la « condensation » des atomes dans le même état quantique fondamental, caractérisé par la même longueur d’onde. Car la mécanique quantique ne regarde plus les atomes comme des petites billes rondes, mais comme des ondes. Et pour ces températures horriblement froides, les ondes individuelles se recouvrent pour n’en faire apparaître qu’une seule. La valse des atomes est parfaitement synchronisée et l’on parle ainsi d’une onde géante ou d’un superatome pour décrire de manière imagée un nouvel état de la matière : le condensat de Bose-Einstein. Notons que les atomes forment un réseau fixe dans un solide ; ils se déplacent suivant des trajectoires chaotiques dans un gaz et glissent les uns sur les autres dans un liquide. Dans un condensat de Bose-Einstein, ils oscillent avec la même longueur d’onde, ce qui est l’une des rares manifestations des propriétés quantiques de la matière à l’échelle macroscopique.
Prédite par Einstein en 1925, suite à un calcul inspiré par les travaux du physicien indien Satyendra Nath Bose, la condensation d’un gaz ultrafroid a dû attendre soixante-dix ans pour être réalisée expérimentalement. Les Américains Carl Wieman et Eric Cornell, et l’Allemand Wolfgang Ketterle ont obtenu pour la première fois, en 1995, un condensat de Bose-Einstein. Cette réalisation, attendue avec impatience par le monde scientifique, a été récompensée rapidement par le prix Nobel de physique en 2001. Quatre ans plus tôt, le même prix était attribué au Français Claude Cohen-Tannoudji et aux Américains William Phillips et Steven Chu pour la mise au point des techniques de refroidissement des atomes par laser, techniques qui ont ouvert la voie à la réalisation du condensat.
Aujourd’hui, il existe dans le monde plus de trente laboratoires de recherche pouvant réaliser le condensat de Bose-Einstein, dont deux en France : le laboratoire Kastler-Brossel de l’École normale supérieure et l’Institut d’optique d’Orsay. Néanmoins, une telle expérience reste très coûteuse, avec un coût de l’équipement supérieur à 100 000 euros, ce qui devrait nous « refroidir » dans notre tentative, même imaginaire, de réaliser le « café » superfluide.
Un autre système manifeste des propriétés superfluides : l’hélium liquide, quand il est refroidi « seulement » à une température inférieure à 2,2 kelvins (soit environ – 271 °C). La nature de la superfluidité, dans ce cas, est différente de celle décrite par Einstein pour la condensation gazeuse.
La simulation numérique comme outil d’exploration
La formidable cohérence du condensat de Bose-Einstein et sa haute contrôlabilité laissent présager des applications qui pourraient apporter une véritable révolution technologique. La construction d’un laser à atomes pour graver des circuits électroniques à l’échelle atomique, l’amélioration — d’un facteur inimaginable de 100 milliards — de la précision des instruments de mesure du temps (horloges utilisées, par exemple, dans les GPS) ou de la position (gyroscopes laser pour les avions et les sondes spatiales) font partie des applications envisageables. On parle aussi du condensat de Bose-Einstein comme étant une voie possible pour la réalisation d’un objet technologique qui tient actuellement de la science-fiction : l’ordinateur quantique.
Il faut néanmoins savoir que le condensat produit en laboratoire est un objet minuscule d’environ 0,1 millimètre (ou 100 micromètres), entouré d’un nuage d’atomes non condensés. L’observation expérimentale est d’autant plus délicate que cette assemblée atomique est placée dans un piège magnétique. En effet, pour atteindre des températures proches du zéro absolu, les atomes ne doivent pas entrer en contact avec des parois, d’où la nécessité de les mettre en suspension dans un champ magnétique fort, généré par deux grosses bobines.


En haut (© Jean Dalibard / CNRS) : expérimentation en rotation rapide (plus la vitesse est importante, plus le contraste est faible ; voir figures e, f et g). En bas (© Ionut Danaila) : simulation numérique en 3D de l’expérience en laboratoire, montrant l’évolution du réseau de tourbillons quantifiés vers une structure particulière, avec un trou au centre.
Pour prendre des photographies, le piège magnétique est coupé, puis un bref éclair lumineux est envoyé à travers l’assemblée atomique afin de mesurer son absorption et d’évaluer ainsi sa densité. Malgré la difficulté de la tâche, les photos expérimentales montrent remarquablement bien la structure du condensat, en particulier la présence de tourbillons quantiques (voir les photographies ci-dessus). Cependant, certains régimes, comme celui de la rotation rapide, sont difficiles à explorer expérimentalement. La simulation numérique peut alors apporter un complément d’information nécessaire à la compréhension des phénomènes et à la validation des théories physiques ; elle permet aussi une exploration détaillée de la structure tridimensionnelle (3D) du condensat et des lignes de tourbillon, ce qui est difficile — voire impossible — à visualiser dans les expériences de laboratoire.
Si l’on ajoute à l’argumentaire précédent le fait que le développement vertigineux des ordinateurs a rendu le coût de la simulation numérique très accessible, on peut se demander légitimement pourquoi l’expérimentation numérique ne remplace pas complètement l’expérience en laboratoire. Tout simplement parce que l’approche numérique est soumise à une série d’approximations (modèles physiques et mathématiques), tandis que la vraie « physique » des phénomènes est observée en laboratoire. Parfois, même les plus puissants ordinateurs d’aujourd’hui ne peuvent pas offrir la capacité de calcul nécessaire à la résolution précise des modèles utilisés. Pour ces raisons, l’expérience en laboratoire et le calcul numérique restent des outils complémentaires dans l’exploration de la physique. En revanche, il existe des domaines où la simulation numérique est privilégiée par rapport à l’expérience et la remplace partiellement (conception des avions, automobiles) ou même totalement (essais nucléaires).
Au cœur du dispositif numérique
Le point de départ de l’aventure numérique est constitué par l’équation modèle qui décrit mathématiquement le phénomène physique. C’est habituellement le rôle des physiciens de mettre en équation les lois de la nature. Le modèle mathématique ainsi obtenu se présente généralement sous la forme d’une équation aux dérivées partielles, ou d’une équation intégrale. Les dérivées partielles sont généralement celles de la fonction inconnue par rapport aux variables d’espace (x, y, z) et de temps (t). La forme intégrale des équations est plus appropriée pour exprimer les lois de conservation de la physique (conservation de la masse, de l’énergie, etc.).
Les propriétés intrinsèques de l’équation modèle (existence, unicité des solutions, etc.) sont ensuite étudiées par les mathématiciens dans un cadre théorique abstrait. Les informations ainsi fournies sont utilisées en mathématiques appliquées ou en physique pour proposer des méthodes numériques adaptées à la résolution sur ordinateur de l’équation modèle. Les dernières étapes de la simulation numérique sont constituées par l’implémentation sur ordinateur (programmation de la méthode), le calcul proprement dit (qui peut varier de quelques secondes à plusieurs mois, en fonction de la complexité du problème) et l’exploitation des résultats.
Regardons ces étapes en détail dans le cadre de la simulation d’un condensat de Bose-Einstein. Nous nous rappelons que les atomes du condensat oscillaient avec la même longueur d’onde. Cette caractéristique permet de décrire le condensat en oubliant sa composition atomique (microscopique) et en utilisant une seule variable à l’échelle macroscopique. Cette variable est un nombre complexe, appelé « fonction d’onde » et noté par Ψ. L’équation qui décrit l’évolution de la fonction d’onde est due à deux physiciens, l’Américain Eugene Gross (1926-1991) et le Russe Lev Pitaevskii (actuellement professeur à l’université de Trente, en Italie). L’équation de Gross-Pitaevskii est une forme particulière de l’équation de Schrödinger, bien connue dans la mécanique quantique.
Une fois l’équation connue et son analyse mathématique réalisée, on passe à sa résolution numérique. Comme les ordinateurs fournissent des valeurs discrètes, on ne peut calculer qu’une approximation de la vraie solution. Seul un nombre fini de points du domaine du condensat sera donc calculé. Ces points sont distribués dans un « maillage ».
Il s’agit ici d’une représentation schématique d’une grille de calcul (ou maillage) en deux dimensions (x, y) de l’espace, pour deux méthodes représentatives du calcul numérique.
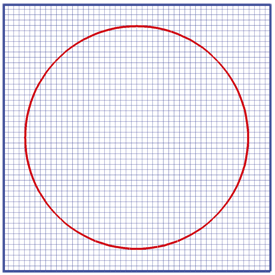
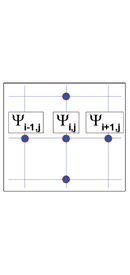
La « méthode des différences finies » utilise un quadrillage rectangulaire du domaine de calcul qui englobe le domaine occupé par le condensat (cercle rouge). La variable inconnue Ψ sera calculée aux points discrets identifiés par deux indices (i, j), suivant les directions x et y. La forme différentielle de l’équation modèle est utilisée pour cette méthode.
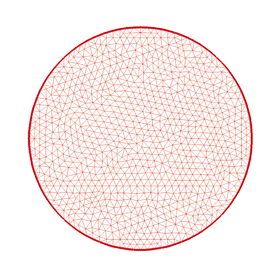
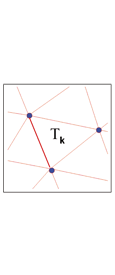
La « méthode des éléments finis » offre plus de flexibilité dans la définition du domaine de calcul, qui peut avoir des frontières de forme complexe. Dans cet exemple, des éléments triangulaires sont utilisés pour couvrir exactement le domaine du condensat. La variable inconnue Ψ sera calculée aux sommets de chaque triangle Tk. La méthode utilise une forme intégrale de l’équation modèle.
Ces deux méthodes peuvent être généralisées en 3D : les cellules rectangulaires deviennent alors des briques parallélépipédiques et les triangles des tétraèdres.
Images © Ionut Danaila.
L’implémentation des méthodes et algorithmes passe par une phase de programmation qui génère des « codes de calcul ». Ces programmes fournissent les données numériques qui seront assemblées pour reconstituer l’image numérique du condensat. Comment savoir que les nombres fournis par l’ordinateur sont pertinents ? Tout d’abord, c’est l’analyse numérique – une branche des mathématiques appliquées – qui fournit la preuve que les méthodes et les algorithmes utilisés sont corrects. Ensuite, la validation ultime des résultats est donnée par la confrontation avec les mesures expérimentales.
Plus loin que l’expérience en laboratoire
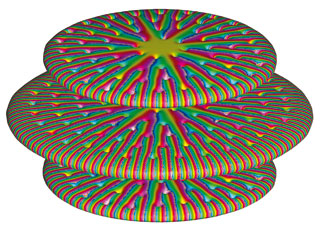
La plus grande satisfaction d’un « numéricien » est de voir ses équations et ses lignes de code se métamorphoser en vrai banc expérimental. Une fois le système numérique validé, il peut être utilisé dans l’expérimentation numérique, c’est-à-dire pour calculer des situations non explorées en laboratoire, permettant ainsi d’aller plus loin pour approfondir la connaissance des phénomènes simulés. Les deux figures montrent des configurations simulées mais non réalisées, pour l’instant, en laboratoire. Imaginer et simuler de nouvelles configurations permet de stimuler les développements théoriques et de suggérer de nouvelles applications.

Réseau en rotation de trois condensats en forme de galette (en haut, à droite) et vortex géant (ci-dessus). Les couleurs mettent en évidence les discontinuités introduites par les tourbillons quantifiés.
Si la simulation numérique est devenue un outil incontournable dans tous les domaines de la science, nous sommes néanmoins loin de l’image véhiculée dans les films de science-fiction, avec des programmes d’ordinateur intelligents qui renvoient immédiatement à l’écran une jolie image tridimensionnelle du problème simulé, comportant toutes les valeurs nécessaires à son analyse. Un important travail mathématique et informatique ainsi que beaucoup de savoir-faire sont encore nécessaires pour obtenir ce genre d’informations. Même si la recherche fondamentale dans ces domaines contribue, chaque jour, à se rapprocher de cet idéal, l’expertise du chercheur reste un facteur primordial dans la réussite d’une simulation numérique.
- DALIBARD Jean, « La condensation de Bose-Einstein en phase gazeuse », in Images de la physique, 2001.
- DANAILA Ionut, « Tourbillons en fluides et superfluides : une exploration numérique », mémoire de HDR (habilitation à diriger des recherches), 2008.
- « Le condensat de Bose-Einstein : la matière qui vient du froid », in Science & Vie, hors série n° 228, septembre 2004.
Cet article est paru dans la revue Textes et Documents pour la Classe n°997 L’informatique éditée en partenariat avec l’Inria.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Ionut Danaila
Maître de conférences au laboratoire Jacques-Louis Lions, Université Pierre et Marie Curie.