Vérifier la sécurité de nos communications

De plus en plus de communications sont dématérialisées du fait de l’essor des moyens de communications numériques : email, messagerie instantanée, commerce en ligne, etc. Afin d’assurer la sécurité de ces échanges, de nombreux protocoles utilisant la cryptographie ont vu le jour. Il existe deux familles d’algorithmes de chiffrement : les algorithmes symétriques comme le chiffrement historique de Vigenère [4] ou AES [7] et les algorithmes asymétriques aussi appelés algorithmes à clé publique comme RSA [10].

Le chiffrement symétrique

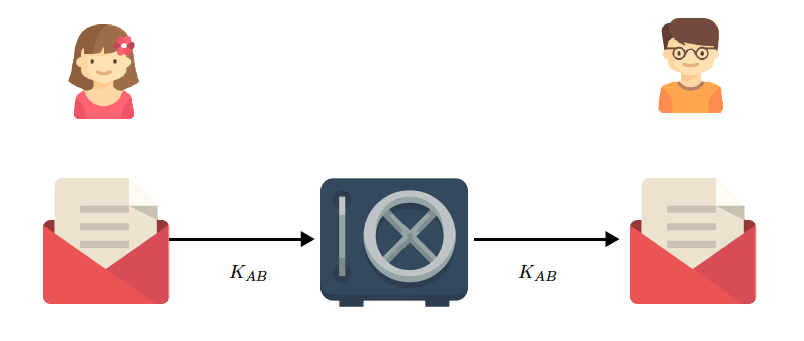
Dans un chiffrement symétrique, deux personnes souhaitent communiquer de manière chiffrée. Ici Alice et Bob, que nous identifions respectivement par A et B, possèdent la même clé symétrique K_AB. Ainsi, comme expliqué sur le dessin ci-dessous, Alice chiffre avec la clé K_AB son message puis l’envoie à Bob. Une fois le message chiffré reçu, Bob peut le déchiffrer en utilisant la même clé K_AB puis le lire. Ces chiffrements sont dits symétriques car la même clé est utilisée pour chiffrer et déchiffrer.

Le chiffrement asymétrique

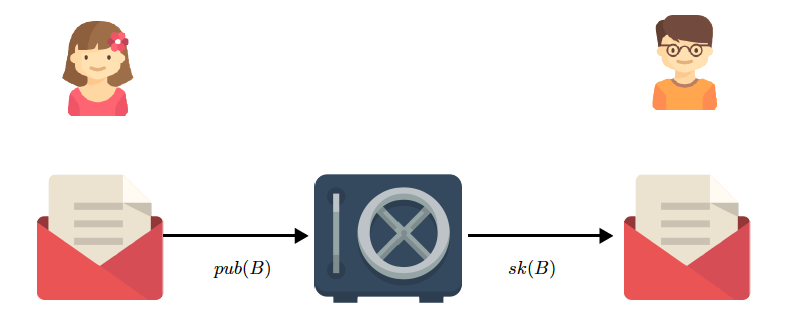
Le chiffrement asymétrique fonctionne différemment. Chaque participant possède une clé publique et une clé secrète. Pour Alice, nous noterons pub(A) sa clé publique et sk(A) la clé secrète associée. Tous les participants connaissent les clés publiques de tous les autres car elles sont publiées dans des annuaires sur Internet. Chaque participant a intérêt à publier sa clé publique car elle sert à générer des messages chiffrés pour lui. Par exemple, si Alice veut envoyer un message chiffré à Bob, il lui suffit de trouver la clé publique de Bob, pub(B), sur Internet, puis de chiffrer le message avec celle-ci et de l’envoyer à Bob. Une fois le message reçu, Bob utilise la clé secrète sk(B) pour déchiffrer le message. Seul Bob peut lire le message car lui seul possède la clé secrète pour le déchiffrer.

Le problème de l’échange de clé

La cryptographie à clé publique permet à une personne d’envoyer une information chiffrée sans aucun échange au préalable, en utilisant par exemple le chiffrement RSA. Malheureusement, toutes les communications ne peuvent pas s’effectuer avec un tel chiffrement. En effet, il faut environ 30 secondes avec un ordinateur de bureau pour chiffrer un message de 10 Mo avec RSA, alors qu’il ne faut que 0,1 secondes pour chiffrer avec AES.

Afin d’avoir le meilleur des deux mondes, nous allons utiliser la cryptographie à clé publique pour échanger une clé symétrique entre Alice et Bob. Ainsi ils pourront communiquer en toute sécurité en utilisant cette nouvelle clé. Les protocoles cryptographiques permettant cela sont appelés protocoles d’échange de clé.

Le protocole de Needham-Schroeder

En 1978, un an après la publication de RSA, le premier chiffrement à clé publique, R. Needham et M. Schroeder [9] proposèrent un protocole d’échange de clé symétrique entre deux participants, Alice et Bob. Ces deux participants veulent échanger en toute sécurité une nouvelle clé symétrique K. Le protocole utilise un algorithme de chiffrement asymétrique et il fonctionne comme suit :

a) Alice envoie à Bob un message chiffré par la clé publique de Bob, pub(B). Il contient son identité A et un nombre aléatoire N_A« fraîchement » choisi par Alice, aussi appelé nonce.
b) Une fois ce message reçu, Bob choisit une nouvelle clé symétrique, notée K pour communiquer avec Alice. Il répond à Alice en envoyant cette nouvelle clé K, ainsi que le nonce N_A précédemment reçu, dans un message chiffré par la clé publique d’Alice, pub(A).
c) Alice confirme à Bob qu’elle a bien reçu le message, en lui renvoyant le K chiffré par pub(B), la clé publique de Bob.

Une fois le protocole terminé, Alice est convaincue d’avoir effectué une session du protocole avec Bob, car il lui a renvoyé son nonce N_A. De même, Bob pense avoir communiqué avec Alice. Ils partagent alors une information commune K qui sera la clé publique utilisée dans leurs communications futures. Ils pensent également qu’ils sont les seuls à connaître la clé symétrique K.

L’attaque « de l’homme du milieu » de Gavin Lowe

Ce protocole est célèbre car, dix-sept ans après sa publication, une attaque fut découverte. Elle fit prendre conscience qu’un protocole, dont toutes les informations transmises sont cryptées par un chiffrement asymétrique sûr mais qui utilise un canal de communication accessible à tous, n’est pas nécessairement un échange de messages sûr. De par la conception même du protocole, des informations confidentielles peuvent être découvertes par un intrus.

Gavin Lowe trouva cette attaque en utilisant un outil automatique de vérification de protocoles cryptographiques [8]. Cette attaque permet à un intrus, appelé Charlie et identifié par C, d’obtenir la clé secrète K échangée par Alice et Bob.

Cette attaque est un exemple d’intrusion connu sous le nom de « man in the middle », car Charlie est placé entre Alice et Bob. Il joue en parallèle deux sessions du protocole, une avec Alice et une avec Bob. Il peut par exemple se placer entre les deux interlocuteurs qui communiquent en utilisant une communication sans fil, ou bien simplement se placer sur le réseau. Voyons plus précisément comment l’attaque fonctionne.

Alice commence une session du protocole avec Charlie en suivant la première étape du protocole. Elle utilise la clé publique de Charlie et lui envoie un premier message. Charlie peut alors déchiffrer le message avec sa clé secrète. Il récupère ainsi l’identité d’Alice A et son nonce N_A. L’intrus peut ensuite commencer une deuxième session avec Bob, en se faisant passer pour Alice. Il envoie à Bob un message chiffré avec la clé publique de Bob contenant l’identité d’Alice A et le nonce N_A, comme l’indique la première étape du protocole.

D’après le message qu’il a reçu, Bob pense parler en toute sécurité à Alice, alors qu’il communique en fait avec Charlie. Il répond donc, comme l’indique la seconde étape du protocole, en envoyant un message qui contient le nonce N_A et la clé symétrique K qu’il vient de générer, et en chiffrant ce message avec la clé publique d’Alice. Charlie ne peut pas le déchiffrer, n’ayant pas la clé secrète d’Alice. Il le transfère donc à Alice.

Après avoir déchiffré le message reçu, Alice renvoie la clé K comme cela est spécifié dans le protocole. Ainsi Charlie reçoit le message, et le déchiffre, car Alice a utilisé la clé publique de l’intrus. Celui-ci conclut alors le protocole initié avec Bob, en envoyant K chiffré avec la clé publique de Bob.

Rappelons que le protocole sert à échanger la clé symétrique K entre Alice et Bob. L’intrus connaît maintenant cette clé, il peut alors continuer sans aucun problème à écouter les messages envoyés par Bob à Alice, les déchiffrer et même, se faire passer pour Alice. En effet, il peut répondre à Bob en chiffrant ses réponses grâce à la clé symétrique K.

Correction de la faille de sécurité

Afin de corriger cette attaque, il suffit que Bob ajoute son identifiant dans sa première réponse à Alice. Il envoie donc son identifiant B, le nonce N_A, et la clé symétrique K. Quand Alice reçoit le message, elle s’aperçoit qu’elle discute avec deux personnes à la fois, car la clé associée à l’identifiant B ne correspond pas à la clé publique de Charlie pub(C). Alice arrête le protocole et empêche l’intrus d’apprendre le secret. L’attaque ne fonctionne plus.

Vérification formelle pour les protocoles cryptographiques

Utiliser un algorithme de chiffrement incassable est un prérequis indispensable pour assurer la sécurité mais n’est pas suffisant, comme illustré ci-dessus avec le protocole de Needham-Schroeder. En effet, en combinant plusieurs échanges de messages, un intrus peut obtenir de l’information si le protocole est mal conçu. Par exemple, l’attaque de Gavin Lowe permet de récupérer la clé secrète du chiffrement symétrique. Ce genre d’attaque est appelée attaque logique.

Pour attaquer un protocole cryptographique, il existe une autre approche, qui consiste à essayer d’obtenir de l’information sur les messages chiffrés échangés, par exemple en les déchiffrant ou en cherchant à obtenir la clé utilisée. Ces attaques sont appelées cryptanalyses et portent sur la sécurité de l’algorithme cryptographique employé [6].

La sécurité des protocoles de communication utilise des fonctions mathématiques pour chiffrer les messages. Bien que nécessaires, ces techniques n’assurent pas forcément le secret des communications, comme le montre l’attaque sur le protocole de Needham-Schroeder. Construire de tels protocoles de manière sécuritaire n’est pas une tâche facile et dépasse largement les capacités humaines.

Pour le protocole de communication de Needham-Schroeder qui n’a que trois messages, il a fallu dix-sept ans pour découvrir une attaque, qui une fois présentée semble relativement simple. Sa découverte fut le point de départ de la vérification formelle pour les protocoles cryptographiques. Depuis, les chercheurs ont développé avec succès des techniques de vérification automatique. Ces outils permettent de garantir l’absence de faille de sécurité face à un intrus, ou bien de découvrir des failles et de les corriger.

Pour vérifier qu’un protocole cryptographique est sûr, il faut modéliser plusieurs éléments : le protocole, la propriété de sécurité et l’attaquant contre lequel le protocole doit être sûr. Chacune de ces étapes nécessite de trouver le bon niveau d’abstraction, c’est-à-dire le bon compromis entre abstraction et efficacité de la vérification. Il existe de nombreux outils de vérification [1, 3, 2, 5], qui permettent aujourd’hui de vérifier automatiquement le secret et l’authentification. Ces outils ont par exemple permis de vérifier un protocole d’échange de mails [11].

Il reste encore de nombreuses techniques à développer pour vérifier automatiquement les propriétés de sécurité des protocoles à venir de par les nouvelles fonctionnalités désirées, mais aussi la complexité des protocoles et primitives cryptographiques utilisés…