Qu’est-ce qu’un algorithme ?

Le mot « algorithme » vient du nom du grand mathématicien persan Al Khwarizmi (vers l’an 820), qui introduisit en Occident la numération décimale (rapportée d’Inde) et enseigna les règles élémentaires des calculs s’y rapportant. La notion d’algorithme est donc historiquement liée aux manipulations numériques, mais elle s’est progressivement développée pour porter sur des objets de plus en plus complexes, des textes, des images, des formules logiques, des objets physiques, etc.

De la méthode

Un algorithme, très simplement, c’est une méthode. Une façon systématique de procéder pour faire quelque chose : trier des objets, situer des villes sur une carte, multiplier deux nombres, extraire une racine carrée, chercher un mot dans le dictionnaire… Il se trouve que certaines actions mécaniques – peut-être toutes ! – se prêtent bien à la décortication. On peut les décrire de manière générale, identifier des procédures, des suites d’actions ou de manipulations précises à accomplir séquentiellement. C’est cela, un algorithme. En tant que méthode, il répond donc à des questions du type : « comment faire ceci ? », « obtenir cela ? », « trouver telle information ? », « calculer tel nombre ? ». C’est un concept pratique, qui traduit la notion intuitive de procédé systématique, applicable mécaniquement, sans réfléchir, en suivant simplement un mode d’emploi précis.

Un exemple commun est par exemple la recherche d’un mot dans le dictionnaire. On regarde d’abord la première lettre du mot, et on la compare avec celle des mots de la page où le dictionnaire est actuellement ouvert. Suivant la position relative des deux lettres en question dans l’ordre alphabétique, on tourne alors les pages en avant ou en arrière, jusqu’à ce que les premières lettres coïncident. Puis on reproduit la même procédure avec la deuxième lettre du mot, puis la troisième, et ainsi de suite… Cet algorithme familier nous indique que les objets manipulés ne sont pas nécessairement des nombres ou des objets mathématiques. Ici, ce sont des mots, ou des lettres. De plus, on comprend que pour qu’un algorithme soit applicable, il faut que les objets manipulés se présentent sous un format bien précis, qui assure à la fois l’efficacité et la généralité du procédé. En l’occurrence, s’il s’agit d’un dictionnaire français, il faut que les mots recherchés soient des mots français écrits en lettres latines, et surtout que, dans le dictionnaire, les mots soient bien classés par ordre alphabétique !

Du nombre à l’information

La vertu essentielle des algorithmes est de permettre l’exécution optimisée de procédés répétitifs, essentiellement grâce à la formalisation et à la description des enchaînements logiques à un niveau plus abstrait, et donc plus général. Ils s’étendent ainsi à des domaines de la société toujours plus nombreux et plus inattendus. Cette généralisation a accompagné le développement des langages de programmation depuis les années soixante, qui permettent aujourd’hui la manipulation de structures et d’objets ayant des propriétés et des comportements analogues à ceux du monde ordinaire. Leur relation avec les couches profondes du traitement informatique est assurée après coup par le compilateur, de manière transparente pour le programmateur et le concepteur d’algorithmes.

En définitive, le codage numérique des objets manipulés (au niveau informatique) est devenu secondaire pour l’algorithmique. L’essentiel est de percevoir les éléments clés d’un processus de calcul, ou d’un procédé quelconque, et d’imaginer les suites d’opérations logiques les plus astucieuses et les plus efficaces pour le mettre en œuvre de façon automatique et performante. L’algorithme est donc en réalité le squelette abstrait du programme informatique, sa substantifique moelle, indépendante du mode de codage particulier qui permettra sa mise en œuvre effective au sein d’un ordinateur ou d’une machine mécanique.

L’importance des ordinateurs

Bien avant le premier ordinateur électronique, dans les années trente, les mathématiciens ont découvert un modèle général de machines procédant de manière logique (Logical Computing Machine) – les fameuses machines de Turing, capables d’effectuer mécaniquement tous les algorithmes possibles et imaginables, déjà découverts ou qui le seront jusqu’à la fin des temps. La thèse, dite de Church-Turing, selon laquelle tous les algorithmes sont représentables et effectuables sur une Machine de Turing, est aujourd’hui universellement acceptée. Il a même été démontré de manière formelle que les mécanismes de toutes les machines obéissant aux lois de la physique classique (newtonienne), aussi complexes soient-ils, ne pourront jamais réaliser des opérations qui ne soient pas assimilables (moyennant les correspondances adéquates) à un calcul sur une machine de Turing.

Or une telle machine n’est pas un monstre de complexité que l’humanité devra attendre des millénaires avant de posséder. C’est un modèle d’une simplicité extrême, et nos ordinateurs actuels sont bien plus complexes, dans leur conception et dans leur fonctionnement, qu’une machine de Turing élémentaire. Voilà pourquoi ce qu’une telle machine peut faire, tout ordinateur moderne peut également le faire : calculer tout ce qui est calculable, mettre en œuvre n’importe quel algorithme. Les seules limitations ne sont ni mathématiques, ni conceptuelles, mais liées à la physique : il s’agit de la vitesse de calcul et de la mémoire disponible qui, même si elles augmentent chaque année de manière vertigineuse, ne seront jamais infinies.

D’où l’importance d’identifier des algorithmes efficaces, et de représenter les données utiles de la manière la plus adéquate possible.

Algorithmes en recherche d’efficacité

Quelle que soit leur puissance théorique, les machines informatiques réelles sont soumises à des limitations physiques touchant à la puissance de calcul, c’est-à-dire le nombre d’opérations élémentaires pouvant être effectuées chaque seconde, ainsi qu’à la mémoire disponible, c’est-à-dire la quantité d’informations qu’un programme peut avoir à disposition, ou auxquelles il peut accéder à tout moment en un temps raisonnable.

On peut ainsi évaluer le « coût » d’une opération informatique ou d’un calcul, au sens large, par le temps et la mémoire que nécessite son exécution. Une part importante de la recherche en algorithmique consiste à élaborer des algorithmes de plus en plus efficaces, c’est-à-dire ayant un « coût » le plus faible possible. Il apparaît souvent qu’un effort d’analyse important au moment de la conception permet de mettre au point des algorithmes extrêmement puissants vis-à-vis des applications, avec des gains de temps exceptionnels.

Prenons l’exemple, non mathématique, de l’art du découpage japonais. Pour produire un motif géométrique compliqué dans une feuille de papier, on peut naïvement faire des trous aux ciseaux, un peu partout. Mais cette manière de procéder est à la fois difficile, longue et imprécise. Une autre méthode consiste à effectuer d’abord des pliages astucieux, pour ne donner ensuite que deux ou trois coups de ciseaux dans un coin (ce qui est très facile), et déplier la feuille. Le résultat sera invariablement plus précis (la symétrie étant automatique), et obtenu plus rapidement, avec bien moins de coups de ciseaux. La difficulté a été déplacée dans l’identification du bon algorithme, c’est-à-dire ici la succession et la localisation des pliages et des coups de ciseaux adéquats.

Pour résoudre un même problème, on peut souvent utiliser différents algorithmes, qui n’ont pas tous la même complexité. Ainsi, le calcul du PGCD (plus grand commun diviseur) de deux nombres entiers naturels non nuls peut être effectué de bien des manières. Il est possible de trouver le résultat en essayant la division par tous les entiers, mais le mathématicien grec Euclide a trouvé une méthode plus élégante, connue sous le nom d’algorithme d’Euclide. L’idée est la suivante : on divise le plus grand des deux nombres par le plus petit des deux, puis le plus petit des deux par le reste de la première division euclidienne. On recommence jusqu’à ce que le reste (qui diminue sans cesse) devienne nul. Le PGCD cherché est le dernier reste non nul (ou le premier diviseur, si le premier reste est nul).

L’algorithme d’Euclide. Animation HTML5/JS réalisée par Ouest-INSA.

Parallèlement à l’optimisation des algorithmes, une part importante de la recherche porte sur l’évaluation précise de leurs performances, et notamment sur la façon dont ces performances évoluent avec la taille des objets manipulés. La recherche systématique d’efficacité, si importante lorsqu’il s’agit de résoudre des problèmes complexes ou de fournir des réponses rapides, passe également par la recherche de nouveaux types de représentations ou d’organisations des données. On a vu l’influence des modes de rangement avec l’exemple du dictionnaire. Dans ce cas particulier, comme dans beaucoup d’autres, une structure « en arbres » se révèle particulièrement adaptée.

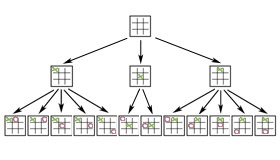
Image d’un arbre de jeu pour le Tic-Tac-Toe.

Un autre exemple, très différent, de l’utilisation de la structure d’arbres en informatique est la notion d’arbre de jeu (game tree) qui permet de modéliser pour un jeu à deux joueurs l’ensemble des enchaînements des différents coups possibles et de leurs ripostes jusqu’à une certaine profondeur.

Donald Knuth, professeur émérite à Stanford, auteur de l’ouvrage de référence sur l’algorithmique, en plusieurs volumes, intitulé « The Art of Computer Programming » (« L’art de la programmation informatique »), considère d’ailleurs les arbres comme « la structure la plus fondamentale de toute l’informatique ».

Si les progrès de la technologie des ordinateurs sont bien connus, avec l’accroissement exponentiel de la puissance de calcul et des capacités de stockage, ceux de l’algorithmique ne sont pas moins extraordinaires. Qu’on pense par exemple aux algorithmes de compression des images ou du son, ou à ceux permettant de calculer la suite des décimales de pi. Si on est passé de quelques milliers de décimales dans les années cinquante, à plus d’un trillion fin 2002, c’est à peu près à part égale en raison des avancées technologiques et algorithmiques.