
Reconstruire des surfaces pour l’imagerie
Lorsqu’on sonde le sous-sol en certains endroits pour connaître la configuration des différentes couches géologiques, ou lorsqu’on veut cartographier un fond marin, le nombre de points de mesure est nécessairement fini. Or il faut reconstruire, à partir des ces données en nombre restreint, les surfaces correspondantes. La situation est analogue avec tous les systèmes d’imagerie informatisés (scanners, télémètres, imageurs tridimensionnels, etc.) utilisés en médecine, dans l’industrie, en archéologie, etc.

Reconstruction d’une turbine.
Comme point de départ, il y a un objet réel – qui peut être une partie du corps humain, une pièce mécanique, un vestige archéologique, une structure géologique, ou autre. De cet objet réel, les instruments ne peuvent enregistrer que certains points à partir desquels on doit reconstruire virtuellement la forme de l’objet. Tel est le problème dit de la reconstruction de surfaces. Il consiste donc à exploiter un nombre fini de points pour fournir une représentation géométrique et informatique de l’objet, ce qui permettra de le visualiser sur un écran, de l’archiver dans la mémoire de l’ordinateur, de procéder aisément à des calculs, voire de modifier l’objet ou d’en télécommander l’usinage d’une copie. Bref, une fois que la forme d’un objet réel est numériquement enregistrée, et ce, avec suffisamment de précision, on dispose de maintes possibilités d’action et de calcul.
Les enjeux économique et industriel du problème de la reconstruction de surfaces, ainsi que son caractère fondamental du point de vue scientifique, ont conduit à de nombreux travaux depuis une vingtaine d’années. Mais ce n’est que très récemment que les spécialistes ont formalisé en termes mathématiques le problème, ce qui leur a permis de concevoir des algorithmes efficaces et fournissant une reconstruction fidèle. Le transfert vers l’industrie de certains de ces résultats de géométrie dite algorithmique s’est alors opéré de manière très rapide au travers de la création de jeunes pousses (comme Raindrop Geomagic aux États-Unis, ou Geometry Factory issue de notre équipe de recherche) ou le lancement de nouveaux produits par les leaders de la conception assistée par ordinateur ou de l’imagerie médicale (Dassault Systèmes, Siemens Medical).
Diagrammes de Voronoï et triangulation de Delaunay, deux outils géométriques indispensables

Diagramme de Voronoï et triangulation de Delaunay associée.
Le diagramme de Voronoï est modifié à chaque ajout de point.
Pour reconstruire une surface à partir d’un nuage de points qui l’échantillonnent, la grande majorité des algorithmes utilisent un outil central en géométrie algorithmique : la triangulation de Delaunay, nommée d’après Boris Delone (1890-1980), mathématicien russe dont le nom a été francisé en Delaunay.
La triangulation de Delaunay se définit naturellement à partir de ce qu’on appelle le diagramme de Voronoï, du nom du mathématicien russe Georgi Voronoï (1868-1908). Considérons un ensemble fini de points dans l’espace, et appelons-le E. Le diagramme de Voronoï de E est une division de l’espace en cellules convexes (en vert sur la figure ci-contre), où chaque cellule est constituée des points de l’espace plus proches d’un point de E que des autres points de E. Les cellules – ce sont des polyèdres convexes – sont ainsi définies de manière univoque. Maintenant, relions par des segments de droite les points de E dont les cellules de Voronoï sont adjacentes. L’ensemble de ces segments (en bleu sur la figure) constitue la triangulation de Delaunay associée à E.
L’animation suivante montre la construction du diagramme de Voronoï et de la triangulation de Delaunay à partir des points que vous choisissez.
Animation en HTML5/JS réalisée par Marc Delorme d’après une applet Java de Paul Chew, adaptée en français pour Interstices avec son aimable autorisation. Accéder aux sources.
Pour définir des points, cliquez dans la fenêtre rouge. Le menu du haut vous permet d’afficher soit le diagramme de Voronoï (sur fond rouge), soit la triangulation de Delaunay (sur fond vert), en conservant les points que vous avez choisis. Utilisez le bouton Effacer pour repartir à zéro. Le menu du bas vous permet de visualiser en surimpression les cercles circonscrits ou les arêtes.
Ces structures se définissent dans des espaces de dimension quelconque ; c’est le cas de la dimension trois – l’espace usuel – qui est le plus intéressant pour la reconstruction de surfaces. Les diagrammes de Voronoï figurent parmi les principaux sujets d’étude de la géométrie algorithmique, et c’est dans les années quatre-vingts que l’on a établi leur lien avec la théorie des polytopes (analogues des polyèdres dans les espaces de dimension supérieure à trois). Leur étude dans le contexte de l’échantillonnage des surfaces est beaucoup plus récente.
Quel est l’intérêt des diagrammes de Voronoï et des triangulations de Delaunay ? Si E est un échantillon de n points pris sur une surface S, on peut montrer que son diagramme de Voronoï et la triangulation de Delaunay correspondante contiennent beaucoup d’informations sur cette surface. Lorsque l’échantillonnage est suffisamment dense, on peut fournir des approximations précises de la surface. Par exemple, le vecteur qui joint un point P de E au sommet le plus éloigné de sa cellule de Voronoï est une bonne approximation de la normale à la surface S au point P.
Il faut s’assurer que les temps de calcul resteront raisonnables, que les algorithmes sont fiables
C’est ainsi que l’on connaît aujourd’hui plusieurs algorithmes de reconstruction capables, à partir d’un échantillon fini de points d’une surface S, de construire une surface S’ qui approxime correctement la surface réelle S. Qui plus est, la théorie de ces algorithmes permet de calculer une borne qui dépend évidemment de la densité d’échantillonnage.
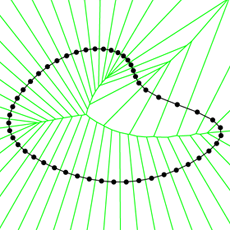
Diagramme de Voronoï d’un ensemble de points pris sur une courbe (image : Dominique Attali).
Comme les jeux de données fournis par les instrument de mesure comportent généralement plusieurs centaines de milliers de points, voire des millions, les questions combinatoires et algorithmiques jouent un rôle critique. Il est par exemple important de savoir si la quantité de calculs que nécessite la triangulation de Delaunay restera ou non dans une limite raisonnable. Dans les cas les plus défavorables, le nombre T d’étapes de calcul (c’est-à-dire, en fin de compte, le temps de calcul) peut être quadratique ; autrement dit, T est au pire proportionnel au carré du nombre de points de l’échantillonnage. On suppose toutefois que cette situation ne se produit pas dans le cas de surfaces bien échantillonnées. Des résultats plus précis ont été démontrés récemment dans le cas de surfaces S polyédriques, c’est-à-dire constituées uniquement de facettes polygonales : pour de telles surfaces et pour des conditions d’échantillonnage faibles, la taille du calcul de triangulation est, au pire, proportionnelle au nombre de points échantillonnés. Le cas des surfaces lisses est plus délicat ; il fait actuellement l’objet de recherches actives.
Les bornes théoriques ne sont pas tout, reste à savoir calculer effectivement et rapidement la triangulation d’un jeu de données. On connaît de nombreux algorithmes. Les plus efficaces sont dits « randomisés » car ils effectuent certains tirages aléatoires au cours de leur déroulement. La théorie des algorithmes randomisés s’est développée très rapidement dans les années quatre-vingt-dix et a conduit à des analyses précises, validées expérimentalement. Dans bien des cas, et le calcul de la triangulation de Delaunay en est un, l’introduction d’une part de hasard autorise à ne pas chercher à résoudre de manière optimale le cas le pire (qui est peu probable) et conduit à des algorithmes simples et très efficaces en moyenne. Aujourd’hui, on réalise le calcul exact de la triangulation de Delaunay tridimensionnelle de un million de points en une minute (avec un processeur à 1,7 GHz et 1 gigaoctet de mémoire).
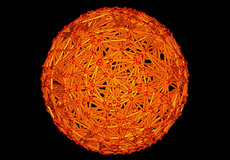
Triangulation de Delaunay 3D calculée par la bibliothèque CGAL.
Si calculer vite est important, calculer de manière fiable l’est encore plus. Cette question est délicate, car les ordinateurs ne savent généralement représenter le nombres qu’avec une précision finie (un nombre fini de décimales). Ainsi, il est impossible de donner une représentation à la fois numérique et exacte de nombres comme π ou √2 qui comportent une infinité de décimales. L’accumulation des erreurs d’arrondis peut alors conduire à un comportement anormal des programmes. Si ces comportements sont bien connus, ils sont difficiles à maîtriser, et la réalisation et la maintenance d’algorithmes fiables sont très coûteuses. Une part importante de la recherche récente en géométrie algorithmique porte sur ces questions et mêle algorithmique, calcul formel (où l’ordinateur manipule des symboles, et non des nombres explicites) et arithmétique des ordinateurs. Elles ont d’ores et déjà débouché sur le développement de bibliothèques de logiciels permettant une programmation facile, efficace et sûre, telle que la bibliothèque CGAL (Computational Geometry Algorithms Library) développée par une collaboration internationale d’universités et d’organismes de recherche.
Une première version de ce texte est parue dans la brochure « L’explosion des mathématiques » éditée par la SMF et la SMAI.
- J.-D. Boissonnat et M. Yvinec, Algorithmic geometry (Cambridge University Press, 1998)
- J.-D. Boissonnat et F. Cazals, « Smooth surface reconstruction via natural neighbour interpolation of distance functions », dans Proceedings of the 16th Annual ACM Symposium of Computational Geometry (2000)
- F. Cazals, J. Giesen, « Delaunay Triangulation based Surface reconstruction : Ideas and Algorithms », Rapport de recherche INRIA (novembre 2004), téléchargeable en pdf.
- le service reconstruction de GEOMETRICA
- le grand projet italo-américain Michelangelo
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Jean-Daniel Boissonnat