Le problème du sac à dos

Cette animation a été réalisée par Ouest INSA, à partir de l’applet réalisée dans le cadre d’un projet étudiant de l’École Polytechnique de l’Université de Tours, par Li Yifang, encadrée par Yannick Kergosien et Jean-Charles Billaut.

Comme vous l’avez peut-être remarqué, le niveau maître n’est déjà pas très facile. Pourtant, il n’y a pas beaucoup d’objets. Ce problème devient vite très compliqué à résoudre de tête lorsque le nombre d’objets est très important. Même les meilleurs algorithmes en informatique ont leurs limites lorsque le nombre d’objet est vraiment grand.

Historique

Ce problème fait partie des 21 problèmes NP-complets identifiés par Richard Karp en 1972. Ces 21 problèmes sont réputés comme les problèmes les plus difficiles en optimisation combinatoire. Un grand nombre d’autres problèmes NP-complets peuvent se ramener à ces 21 problèmes de base.

Nous pouvons retrouver le problème du sac à dos dans de nombreux domaines :

• en cryptographie, où il fut à l’origine du premier algorithme de chiffrement asymétrique en 1976 ;
• dans les systèmes financiers, où l’idée est la suivante : étant donné un certain montant d’investissement dans des projets, quels projets choisir pour que le tout rapporte le plus d’argent possible ;
• pour la découpe de matériaux, afin de minimiser les pertes dues aux chutes ;
• dans le chargement de cargaisons (avions, camions, bateaux…) ;
• ou encore, dès qu’il s’agit de préparer une valise ou un sac à dos pour une randonnée.

Formulation mathématique

Toute formulation commence par un énoncé des données. Dans notre cas, nous avons un sac à dos de poids maximal W et n objets. Pour chaque objet i, nous avons un poids w_i et une valeur p_i.

Pour quatre objets (n = 4) et un sac à dos d’un poids maximal de 30 kg (W = 30), nous avons par exemple les données suivantes :

Ensuite, il nous faut définir les variables qui représentent en quelque sorte les actions ou les décisions qui amèneront à trouver une solution. On définit la variable x_i associée à un objet i de la façon suivante : x_i = 1 si l’objet i est mis dans le sac, et x_i = 0 si l’objet i n’est pas mis dans le sac.

Dans notre exemple, une solution réalisable est de mettre tous les objets dans le sac à dos sauf le premier, nous avons donc : x₁ = 0, x₂ = 1, x₃ = 1, et x₄ = 1.

Puis il faut définir les contraintes du problème. Ici, il n’y en a qu’une : la somme des poids de tous les objets dans le sac doit être inférieure ou égale au poids maximal du sac à dos.

Cela s’écrit : x₁.w₁ + x₂.w₂ + x₃.w₃ + x₄.w₄ ≤ W
ou plus généralement pour n objets :

\begin{align*}\sum_{i=1}^{i=n} x_i . w_i ≤ W\end{align*}

Pour vérifier que la contrainte est respectée dans notre exemple, il suffit de calculer cette somme : 0 × 13 + 1 × 12 + 1 × 8 + 1 × 10 = 30, ce qui est bien inférieur ou égal à 30, donc la contrainte est respectée. Nous parlons alors de solution réalisable. Mais ce n’est pas nécessairement la meilleure solution.

Enfin, il faut exprimer la fonction qui traduit notre objectif : maximiser la valeur totale des objets dans le sac.

Pour n objets, cela s’écrit :

\begin{align*}\text{ max } \sum_{i=1}^{i=n} x_i . p_i\end{align*}

Dans notre exemple, la valeur totale contenue dans le sac est égale à 10. Cette solution n’est pas la meilleure, car il existe une autre solution de valeur plus grande que 10 : il faut prendre seulement les objets 1 et 2 qui donneront une valeur totale de 11. Il n’existe pas de meilleure solution que cette dernière, nous dirons alors que cette solution est optimale.

Méthodes de résolution

Il existe deux grandes catégories de méthodes de résolution de problèmes d’optimisation combinatoire : les méthodes exactes et les méthodes approchées. Les méthodes exactes permettent d’obtenir la solution optimale à chaque fois, mais le temps de calcul peut être long si le problème est compliqué à résoudre. Les méthodes approchées, encore appelées heuristiques, permettent d’obtenir rapidement une solution approchée, donc pas nécessairement optimale. Nous allons détailler un exemple d’algorithme de résolution de chaque catégorie.

Méthode approchée

Une méthode approchée a pour but de trouver une solution avec un bon compromis entre la qualité de la solution et le temps de calcul. Pour le problème du sac à dos, voici un exemple d’algorithme de ce type :

• DEBUT
• calculer la valeur (p_i / w_i) pour chaque objet i,
• trier tous les objets par ordre décroissant de cette valeur,
• sélectionner les objets un à un dans l’ordre du tri et ajouter l’objet sélectionné dans le sac si le poids maximal reste respecté.
• FIN

Déroulons cet algorithme sur notre exemple :

• Première étape :
  

  Objets	1	2	3	4
  pi / wi	0,54	0,33	0,37	0,30

• Deuxième étape : l’ordre des objets est donc le suivant : 1, 3, 2, et 4.
• Troisième étape :
  • Objet 1 : on le met dans le sac (qui est vide au départ).
  • Objet 3 : on le met dans le sac car l’addition du poids de l’objet 1 et de l’objet 3 est inférieure à 30.
  • Objet 2 : on ne le met pas dans le sac car le poids total (33) dépasse le poids maximal du sac.
  • Objet 4 : on ne le met pas dans le sac pour la même raison que pour l’objet 2.

La solution trouvée est donc de mettre les objets 1 et 3 dans le sac, ce qui donne une valeur de 10. Cette solution n’est pas optimale, puisqu’une solution avec une valeur totale de 11 existe. Néanmoins, cet algorithme reste rapide même si le nombre d’objets augmente considérablement.

Ce type d’algorithme est aussi appelé algorithme glouton, car il ne remet jamais en cause une décision prise auparavant. Ici, lorsque l’objet 2 ne peut pas entrer dans le sac, l’algorithme n’essaie pas d’enlever l’objet 3 du sac pour y mettre l’objet 2 à sa place.

Hormis les algorithmes gloutons, il existe un grand nombre de méthodes approchées : les méthodes de recherche « tabou », les algorithmes génétiques, les algorithmes de descente locale, ou même des algorithmes à base de fourmis artificielles.

Méthode exacte

Pour trouver la solution optimale, et être certain qu’il n’y a pas mieux, il faut utiliser une méthode exacte, qui demande un temps de calcul beaucoup plus long (si le problème est difficile à résoudre). Il n’existe pas une méthode exacte universellement plus rapide que toutes les autres. Chaque problème possède des méthodes mieux adaptées que d’autres. Nous allons présenter un exemple d’algorithme de ce type, nommé procédure par séparation et évaluation (PSE), ou en anglais branch and bound. Nous n’exposerons ici qu’une version simplifiée d’une PSE.

Une PSE est un algorithme qui permet d’énumérer intelligemment toutes les solutions possibles. En pratique, seules les solutions potentiellement de bonne qualité seront énumérées, les solutions ne pouvant pas conduire à améliorer la solution courante ne sont pas explorées. Pour représenter une PSE, nous utilisons un « arbre de recherche » constitué :

• de nœuds ou sommets, où un nœud représente une étape de construction de la solution
• d’arcs pour indiquer certains choix faits pour construire la solution.

Dans notre exemple, les nœuds représentent une étape où un certain nombre d’objets auront été mis dans le sac, d’autres laissés en dehors du sac, et d’autres objets pour lesquels aucune décision n’a encore été prise. Chaque arc indique l’action de mettre un objet dans le sac ou au contraire de ne pas le mettre dans le sac. La figure suivante représente une partie de l’arbre de recherche.

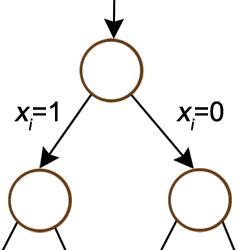
À partir d’une étape N, l’algorithme construit deux nouvelles étapes : dans celle de gauche, on conserve toutes les décisions prises à l’étape N et on ajoute la décision de mettre un nouvel objet (ici l’objet i) dans le sac ; dans celle de droite, on conserve également toutes les décisions prises à l’étape N et on ajoute la décision de ne pas mettre l’objet i.

L’arbre de recherche commence par un seul nœud, où aucune décision n’a été prise pour les objets. Une fois tous les objets sélectionnés, les nœuds finaux, aussi appelés nœuds feuilles, représentent chacun une solution finale. La figure suivante reprend l’exemple précédent et représente l’arbre de recherche induit.

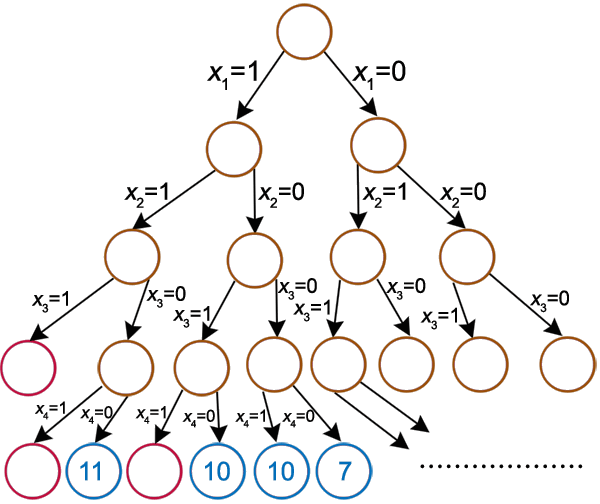
Les nœuds en rouge représentent une solution impossible. Par exemple, pour le nœud tout à gauche en rouge, il est impossible de prendre les trois premiers objets à cause du poids maximal à ne pas dépasser. Il n’est donc pas nécessaire de développer l’étape suivante avec le dernier objet. Les nœuds en bleu sont des nœuds feuilles correspondant à une solution réalisable. À la fin de l’algorithme, il suffit de calculer la valeur du sac pour chaque nœud feuille et de prendre la solution avec la plus grande valeur. La figure n’expose pas tous les nœuds feuilles, étant donné qu’il y en a beaucoup seulement avec 4 objets. Et plus le nombre d’objets augmente, plus le nombre de feuilles augmente rapidement. On parle de croissance exponentielle.

Il existe de nombreuses techniques d’amélioration de parcours de ce type d’arbre. Ces techniques ont pour but de diminuer la taille de l’arbre et d’augmenter la rapidité.

Un élément essentiel dans une PSE est le calcul de bornes, inférieures et supérieures, de la fonction objectif.

• une borne inférieure est une valeur minimum de la fonction objectif. Autrement dit, c’est une valeur qui est nécessairement inférieure à la valeur de la meilleure solution possible. Dans notre cas, une configuration du sac réalisable quelconque fournit une borne inférieure.
• une borne supérieure est une valeur maximale de la fonction objectif. Autrement dit, nous savons que la meilleure solution a nécessairement une valeur plus petite. Dans notre cas, nous savons que la valeur de la meilleure solution est nécessairement inférieure à la somme des valeurs de tous les objets (comme si on pouvait tous les mettre dans le sac).

Nous allons voir maintenant l’utilité de ces bornes. Supposons que la borne inférieure soit initialisée par l’algorithme heuristique vu précédemment. Pendant la recherche à chaque nœud, nous pouvons déterminer une borne supérieure : la somme de toutes les valeurs de tous les objets déjà mis dans le sac plus la somme des valeurs des objets restants dont on ne sait pas encore s’ils seront dans le sac. À partir d’un nœud et de sa borne supérieure, nous savons que les solutions descendantes de ce nœud ne pourront pas avoir une valeur plus grande que cette borne supérieure. Si jamais, à un nœud donné, la valeur de la borne supérieure est inférieure à la valeur de la borne inférieure, alors il est inutile d’explorer les nœuds descendants de celui-ci. On dit qu’on coupe l’arbre de recherche.

En effet, si à partir d’un nœud, nous savons que nous ne pourrons pas faire plus de 20 (borne supérieure calculée) et que la borne inférieure existante est à 21 (on a déjà une solution de valeur 21), alors les solutions descendantes de ce nœud ne sont pas intéressantes.

Enfin, dernière remarque, la valeur de la borne inférieure peut être actualisée lorsqu’est trouvée une solution réalisable qui possède une valeur plus grande.

Ce système de calcul de bornes demande un faible coût de temps de calcul, et permet d’augmenter la rapidité de la PSE puisqu’elle coupe des branches d’arbre pour ne pas perdre de temps à les explorer.

D’autres techniques servent à diminuer la taille de l’arbre et à augmenter la rapidité. Par exemple, elles sont basées sur l’ordre dans lequel on prend les décisions sur les objets, ou sur une évaluation à chaque nœud, ou encore sur des propriétés du problème qui permettent de déduire des conclusions sur certains objets.

Un autre type de méthode exacte qui s’adapte bien pour ce problème de sac à dos est la programmation dynamique. Ce type d’algorithme s’appuie sur le fait que le problème peut se décomposer en sous-problèmes de même nature. L’idée est de fournir une expression de la valeur de la solution optimale sous la forme d’une fonction de récurrence basée sur les valeurs des solutions optimales des sous-problèmes.

Dans le cas du sac à dos, en ne considérant que les i premiers objets, le problème peut être résolu de manière optimale grâce à la solution optimale obtenue avec les i-1 premiers objets. En effet, en notant H(i) la valeur du sac obtenue et en ne considérant que les i premiers objets, les deux solutions pour H(i) sont :

• soit l’objet i est mis dans le sac, donc H(i) = H(i-1) + p_i
• soit l’objet i n’est pas mis dans le sac, donc H(i) = H(i-1)

Cela suppose de connaître la résolution du sous-problème correspondant à H(i-1).

Au final, pour n objets, en partant de H(0)=0, la solution optimale de ce problème du sac à dos correspondrait à H(n). Dans le processus de calcul de la solution optimale, il faut bien évidemment tenir compte de la capacité maximale du sac, à ne pas dépasser.

Un problème toujours d’actualité

Dans la recherche en informatique, le problème du sac à dos et ses dérivés sont encore beaucoup étudiés. Il en existe de nombreuses variantes : sac à dos multi-dimensions (plusieurs poids par objet), plusieurs fonctions objectif, etc. De nombreux algorithmes exacts et approchés sont proposés pour ce type de problèmes. Les chercheurs ne sont pas près de partir en vacances…