
Modélisation géométrique des matériaux nanostructurés
Faire tenir tout le contenu de l’encyclopédie Britannica sur la tête d’une épingle et réorganiser la matière atome par atome… Tel est le défi lancé dans les années soixante par le prix Nobel de physique Richard Feynman. À l’époque, les scientifiques étaient loin de se douter que quarante ans plus tard, cela serait réellement possible. Depuis une dizaine d’années, les nanotechnologies s’immiscent en effet partout et sont devenues en peu de temps un des enjeux scientifiques de demain. Nombreux sont les chercheurs qui, tous domaines confondus et dans le monde entier, travaillent à l’échelle nanométrique. En informatique notamment, les scientifiques travaillent sur de multiples propriétés des nanotechnologies. Dans le cas présent, nous nous intéresserons plus particulièrement à la modélisation de nanomatériaux.
Nanomètre, nanosciences, nanotechnologies

Une boîte de billes ?
Avant de commencer, un petit rappel : un nanomètre (symbole nm) vaut 10-9 m dans le Système International (S.I). Ce milliardième de mètre est à notre échelle une unité extrêmement petite correspondant à la longueur d’une dizaine d’atomes mis bout à bout. Malgré sa taille minuscule, un objet de quelques nanomètres ou même un simple atome est aujourd’hui directement observable grâce au microscope électronique ou à effet tunnel. En outre, il est possible de construire et de manipuler ce type d’objets, obtenant ainsi des propriétés physiques inconnues jusqu’à présent.
Imaginez une boîte remplie de billes plus ou moins grosses, comme celles représentées sur la figure (à droite). En fait, ces billes représentent de manière simplifiée des grains de forme quelconque dont la taille varie typiquement entre 3 et 30 nm. Ces grains sont immergés dans une « matrice » ou « joint de grains » (invisible sur la figure), et la distance entre deux grains n’est jamais inférieure à 1 ou 2 nm. L’agrégat formé par ces grains est modélisé ici par un pavé de dimension 120 x 150 x 150 nm. Mais à quoi peuvent bien servir ces agrégats de grains ?
Comme bien souvent, la nature est un précurseur dans ce domaine et les exemples n’y manquent pas. Ainsi, l’ormeau ou oreille-de-mer (abalone en anglais) est un mollusque dont la coquille nanostructurée évite la propagation de fissures à l’intérieur de celle-ci, ce qui la rend particulièrement résistante. Dans le monde végétal, les feuilles de lotus sont tapissées d’un fin duvet de taille nanométrique qui repousse l’eau, ce qui permet un autonettoyage naturel et lui donne cet aspect immaculé.
L’homme a de fait longtemps utilisé des matériaux nanostructurés sans le savoir. Au Moyen-Âge par exemple, certains vitraux en étaient constitués, ce qui explique leurs superbes variations de couleurs. La réelle prise de conscience des possibilités offertes par cette échelle de taille, on la doit à Richard Feynman, lors de sa célèbre conférence intitulée There is Plenty of Room at the Bottom (« Il y a plein de place en bas ») en 1960. Visionnaire, ce physicien entrevoyait déjà la possibilité de manipuler individuellement des atomes afin de construire de minuscules structures ayant des propriétés remarquables, ou encore de créer des circuits électriques à l’échelle du nanomètre. Bien qu’il n’ait pas vraiment été pris au sérieux à cette époque, la plupart de ses intuitions sont devenues réalité : lithographie des puces en silicium, techniques de microscopie en champ proche, récents circuits d’ordinateurs, etc.
Au cours des deux dernières décennies, de nombreuses sciences et technologies sont entrées dans l’ère « nano » parmi lesquelles l’électronique mais aussi l’optique, la mécanique, la chimie ou la biologie. Malgré les craintes que les nanosciences et nanotechnologies peuvent inspirer, de nombreux progrès sont attendus dans notre environnement quotidien : habitat à surfaces autonettoyantes, textiles offrant un meilleur confort ou une meilleure résistance, voitures plus légères donc moins gourmandes et moins polluantes, sans oublier de nouveaux médicaments se comportant comme des capteurs ou des robots minuscules à l’intérieur du corps humain…
Nanomécanique, matériaux nanostructurés, procédé SMAT
La nanomécanique se propose d’étudier et de caractériser le comportement mécanique de nanostructures en réponse à diverses conditions de charge. L’objectif principal de cette nanoscience est de mieux comprendre et de concevoir de nouveaux matériaux plus légers, plus durs, plus résistants à l’usure, à la fracture et à la fatigue. Les applications potentielles concernent de nombreux secteurs dont l’automobile, l’aéronautique, l’espace, les industries de mise en forme des matériaux, le textile et l’habillement, la médecine, la défense et l’énergie.
 |
 |
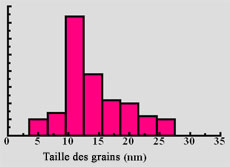 |
| À gauche, une vue par microscopie d’un échantillon de cuivre AVANT nanostructuration. Au centre, une vue APRÈS nanostructuration et à droite, un histogramme de la taille des grains dans ce dernier cas. |
||
Ces matériaux, dits nanostructurés, peuvent être obtenus par divers procédés chimiques, thermiques et/ou mécaniques. Parmi ces derniers, le procédé SMAT (Surface Mechanical Attrition Treatment) permet de générer des nanostructures en surface des matériaux par des déformations plastiques aléatoires et cycliques. En effet, l’observation d’un matériau ordinaire par microscopie montre généralement des grains polyédriques de quelques micromètres (ci-dessus, à gauche). Le procédé SMAT réduit la taille des grains d’un facteur 1000 (passant ainsi à l’échelle du nanomètre) et augmente la proportion des joints de grains (voir la vue par microscopie après nanostructuration ci-dessus, au milieu, et l’histogramme de la taille des grains ci-dessus, à droite). Ce procédé renforce considérablement les matériaux bien qu’il se limite à leur surface. Dans la plupart des cas, la dégradation des matériaux — endommagement, fatigue, corrosion, etc. — s’amorce uniquement en surface. En termes d’amélioration de la durée de vie, ce traitement superficiel produit l’équivalent d’un nanomatériau massif. De plus, si l’on introduit des contraintes résiduelles de compression importantes dans ce matériau, l’effet est encore plus efficace. Par exemple, pour un matériau donné, la nanocristallisation superficielle permet d’améliorer considérablement les propriétés mécaniques des tôles minces.
 |
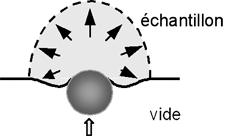 |
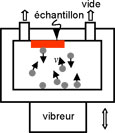
| À gauche, une schématisation du procédé SMAT et à droite, les déformations et contraintes produites par l’impact d’une bille sur l’échantillon. | |
Plus précisément, le procédé SMAT consiste à bombarder dans des directions aléatoires la surface du matériau avec des billes dont l’énergie cinétique est fournie par un vibreur (à gauche). La figure de droite illustre l’impact d’une bille sur la surface du matériau ainsi que la déformation plastique introduite. Ces impacts multidirectionnels permettent d’obtenir une nouvelle classe de matériaux nanostructurés dont la taille des grains varie typiquement entre 3 et 30 nanomètres, sur une épaisseur d’une dizaine à une centaine de micromètres (1 µm = 10-6 m).
Simulation numérique et modélisation géométrique par remplissage
Compte tenu des tailles extrêmement faibles mises en jeu, la simulation numérique du comportement de ces matériaux nanostructurés est indispensable à la compréhension de leurs propriétés mécaniques. Cette simulation requiert à la fois une loi de comportement et une modélisation géométrique de la couche nanométrique. Cette loi de comportement s’obtient généralement à partir d’expériences réelles : traction, compression, etc. En revanche, la modélisation géométrique a fait l’objet de plusieurs études dans lesquelles le domaine nanostructuré est décrit par un rectangle en 2D ou un parallélépipède en 3D, contenant des disques ou des boules dont les rayons sont définis par une distribution donnée. Les disques ou les boules représentent les grains et les espacements entre ceux-ci les joints de grains. Dans la réalité, les grains observés expérimentalement ressemblent plutôt à des polyèdres.
La modélisation des grains par des disques en 2D ou par des boules en 3D simplifie considérablement les calculs géométriques. En outre, elle offre une bonne approximation pour des problèmes complexes où les calculs avec les formes réelles des grains sont très difficiles à réaliser. Plus exactement, cette modélisation simplifiée d’une nanostructure consiste à remplir le domaine avec des disques ou des boules, de telle sorte que :
- la distribution des rayons de ces disques ou boules soit respectée,
- les grains soient séparés par des joints de grains d’épaisseur minimale spécifiée,
- la structure soit la plus dense possible,
- l’assemblage des disques (ou boules) soit le plus irrégulier possible (pas de périodicité pour ne pas fausser la réalité).
Cet assemblage de disques (ou boules) peut éventuellement être transformé via des techniques de triangulation en une structure composée de cellules de Voronoï reflétant mieux la forme polyédrique des grains réels.
Les méthodes de remplissage peuvent être classifiées en deux grandes familles : les dynamiques d’un côté et les constructives de l’autre. Les techniques dynamiques sont basées sur des bougés et/ou des changements de taille des particules. Les mouvements de ces particules peuvent être calculés soit par des modèles purement géométriques (relativement simples), soit par des modèles dynamiques (plus complexes) où chaque particule est dotée d’une ou de plusieurs propriétés physiques lui permettant de trouver une position d’équilibre en fonction de ses interactions avec les autres particules. Les méthodes dynamiques sont souvent très coûteuses en temps de calcul car la position et/ou la taille de chaque grain doit être réévaluée tout au long du processus de remplissage. Cet inconvénient rend ces méthodes moins utilisées que les techniques constructives. Dans ces dernières, les calculs considérés sont purement géométriques, et la position ainsi que la taille des grains sont conservées une fois pour toutes.
Remplissage par une méthode frontale

Maillage frontal 2D. Cette animation illustre la génération d’un maillage d’un rectangle par une approche frontale (les images successives montrant l’évolution du front). Pour lancer l’animation, placez le curseur sur l’image.
Parmi les approches constructives, la méthode frontale offre un moyen puissant pour assurer localement une densité maximale des grains au cours du remplissage. Les grains constituent un front qui se propage du bord vers l’intérieur du domaine ou vice versa, jusqu’au remplissage complet du domaine. Cette approche a été utilisée par plusieurs auteurs sous différentes formes, en particulier les méthodes closed front et inwards packing réciproquement proposées par Feng et Bagi (voir la bibliographie en fin d’article). La méthode closed front commence par construire un front initial réduit à un triangle, ce dernier étant formé par trois particules placées au centre du domaine. Ensuite, chaque nouvelle particule est ajoutée au domaine en l’attachant à deux particules préexistantes. Dans le cas de la méthode inwards packing, le front initial est un ensemble de segments formés par des particules posées contre le côté interne des frontières du domaine. Le remplissage se fait alors vers l’intérieur en suivant une spirale fermée.


À gauche, un remplissage frontal par des disques en 2D et à droite, un remplissage frontal par des boules en 3D. Pour lancer les animations correspondant à chacun des cas, placer le curseur sur chaque image.
Nous proposons une nouvelle variante de la méthode frontale, généralisable en trois dimensions, s’inspirant des techniques de génération de maillage utilisant une approche similaire (ces techniques de maillage frontal et cette nouvelle approche de remplissage frontal ne seront pas détaillées ici mais vous pouvez retrouver les références dans la bibliographie). Rappelons que ces techniques de maillage consistent essentiellement, en supposant qu’une discrétisation du contour du domaine est déjà construite, à appliquer d’une manière itérative les procédures suivantes :
- définir un front constitué de quelques entités du maillage,
- placer des points internes d’une manière optimale par rapport à ce front,
- connecter les nouveaux points générés aux autres entités du maillage déjà existantes, et générer ainsi un nouveau front.
(Revoir l’animation Maillage frontal 2D.)
L’analogie entre cette approche frontale pour le maillage et la nouvelle variante pour l’algorithme de remplissage consiste à assimiler les nœuds à des disques (représentant les grains) et les arêtes (les connectivités du maillage) à des couples de disques voisins. Les rayons des disques sont générés aléatoirement tout en respectant la distribution imposée. Le schéma général de l’algorithme est le suivant :
En plaçant des disques contre la frontière, construire un front initial constitué de segments représentant les couples de disques voisin. Tant que le front n’est pas vide, faire :
- Générer un rayon aléatoirement dans la distribution
- Sélectionner un premier segment du front
- Positionner le disque à insérer par rapport au segment sélectionné
- Détecter les conflits (intersections avec d’autres disques)
- S’il n’y a aucun conflit, accepter le disque, actualiser le front avec les nouveaux couples de disques voisins, et aller en 1
- Sinon, sélectionner un autre segment actif et aller en 3
Le remplissage par la méthode frontale conduit souvent à une hétérogénéité de la densité locale dans la structure, en d’autres termes, certains endroits sont plus denses que d’autres. Ce phénomène peut avoir une incidence directe sur les résultats des simulations numériques des structures granulaires. Ainsi, un algorithme de bougé de disques est appliqué pour rétablir l’homogénéité de l’ensemble. Il s’agit d’une adaptation de l’algorithme de bougé de points, utilisé lui aussi dans le domaine de la génération de maillages. Dans le cas présent, une triangulation est générée à partir du nuage de points formé par les centres des disques. Pour chaque point P de ce nuage, les triangles de sommet P déterminent localement une position idéale P*. Le point P est alors remplacé non pas par P* mais par un point P’ situé sur le segment droit [PP*], cette relaxation ayant pour but d’assurer la convergence de l’algorithme. Le remplacement de P par P’ est effectué à condition que le disque déplacé en P’ ne chevauche aucun disque voisin. À l’issue de cette boucle pour chaque point du nuage, un procédé de bascules d’arêtes assure la régularité de la triangulation.

Diagramme de puissance (ou de Laguerre) généré à partir des disques précédents.
Cette procédure de bougés et de bascules est renouvelée plusieurs fois, produisant finalement une homogénéité globale des disques en 2D ou des boules en 3D.
Pour transformer les disques représentant les grains en cellules polygonales, il suffit de générer un diagramme de puissance (ou de Laguerre) qui est une généralisation du diagramme de Voronoï. En effet, de même que ce dernier est le dual de la triangulation de Delaunay, le premier est le dual de la triangulation de Delaunay pondérée (TDP). Les sommets de cette TDP sont les centres des disques générés précédemment et les poids sont les rayons de ces disques.
Le modèle géométrique continu se fait discret
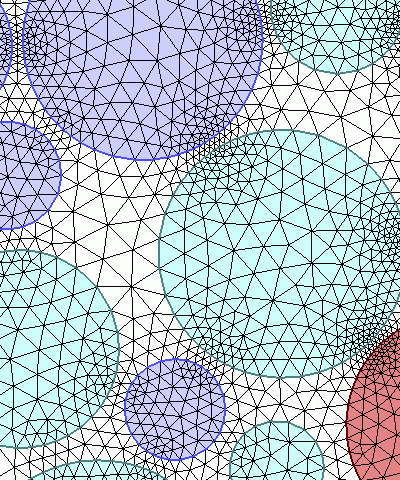

Maillage plan d’un domaine nanostructuré (à gauche) et maillage surfacique d’un autre domaine nanostructuré (à droite). Pour lancer les animations correspondant à chacun des cas, placer le curseur sur chaque image.
Pour effectuer des simulations numériques par la méthode des éléments finis, une discrétisation spatiale – ou maillage – est nécessaire. Par exemple, chaque cercle doit être approché par un polygone et chaque sphère par l’assemblage des faces triangulaires d’un polyèdre. Ce passage d’un modèle continu à un modèle discret est effectué à l’aide des trois logiciels BL2D, BLSURF et GHS3D, développés par l’équipe-projet GAMMA de l’INRIA. Le premier logiciel est un mailleur adaptatif de domaines plans, dans lequel la génération des points internes suit une méthode frontale et la connexion entre ces points est de type Delaunay généralisé. Le deuxième génère des maillages de surfaces composées de carreaux paramétrés, en particulier des sphères, des cônes, des cylindres ou la plupart des surfaces représentées dans les systèmes de CAO (Conception Assistée par Ordinateur). Enfin, le troisième génère des maillages volumiques s’appuyant sur un maillage de surface. Dans ce cas, un nombre très important d’éléments est généré, de l’ordre de plusieurs dizaines de millions de tétraèdres. Ainsi, il est nécessaire de mettre au point des algorithmes de partitionnement de domaine, dans le but de paralléliser tant la construction du maillage que la simulation numérique effectuée sur ce modèle discret. Des études sont en cours afin de réaliser cet objectif.
Les nanostructures générées dans les zones proches de la surface augmentent la résistance des matériaux mais en contrepartie diminuent leur ductilité sur les faces externes. De tels traitements surfaciques permettent de créer de nouveaux matériaux plus résistants pour l’aéronautique, l’automobile, etc. Cependant, un traitement volumique s’avère nécessaire pour l’amélioration de la ductilité. Dans ce cas, de nouveaux procédés de colaminage de couches nanostructurées sont en cours d’élaboration. Le nouveau matériau ainsi fabriqué sera composé de plusieurs couches « soudées » entre elles et présentera des propriétés quasi équivalentes dans tout le volume. La modélisation et la simulation du comportement de ce dernier type de matériaux, composés de grains à l’échelle nano et micro, ainsi que la mise au point de procédés industriels innovants, présenteront des grands défis en mécanique des structures dans les années à venir.
En francais
- A. Nouailhat, Introduction aux nanosciences et aux nanotechnologies, Hermès-Lavoisier, 2006.
- J.D. Boissonnat, M. Yvinec, Diagrammes de Voronoï, part. 5, pp. 425-513, in Géométrie algorithmique, Ediscience international, 1995.
- R. Löhner, La méthode frontale, chap. 3, pp. 105-138, in Traité en Mécanique et Ingénierie des Matériaux – Méthodes Numériques – Maillage et adaptation, sous la direction de P.L. George, Hermès, Paris, France, 2001.
- H. Borouchaki, La marche unité, chap. 4, pp. 139-171, in Traité en Mécanique et Ingénierie des Matériaux – Méthodes Numériques – Maillage et adaptation, sous la direction de P.L. George, Hermès, Paris, France, 2001.
- A. Benabbou, H. Borouchaki, P. Laug, J. Lu, Modélisation géométrique, maillage et simulation de structures granulaires. Application aux nanostructures (Rapport de Recherche INRIA, à paraître).
- P.J. Frey, P.L. George, Maillages : applications aux éléments finis, Hermès, 1999.
En anglais
- C.P. Poole, F.J. Owens, Introduction to nanotechnology, Wiley, 2003.
- W.K. Liu, E.G. Karpov, H.S. Park, Nano Mechanics and Materials – Theory, Multiscale Methods and Applications, Wiley, 2006.
- Y. T. Feng, K. Han and D. R. J. Owen. Filling domains with disks: an advancing front approach. International Journal for Numerical Methods in Engineering. Volume 56, Issue 5, Pages 699 – 713, 26 Nov 2002.
- K. Bagi. An algorithm to generate random dense arrangements for discrete element simulations of granular assemblies. Granular Matter (2005) 7: 31–43.
- H. Borouchaki, P. Laug, P.L. George, Parametric surface meshing using a combined advancing-front — generalized-Delaunay approach, International Journal for Numerical Methods in Engineering (IJNME), Wiley, vol. 49, no. 1-2, pp. 233–259, Sept. 2000.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Houman Borouchaki
