Nombres premiers et cryptologie : l’algorithme RSA

Les nombres premiers ont depuis toujours fasciné les mathématiciens. Pourquoi ? Parce que bien qu’ils soient définis par une propriété simple — un nombre premier est un entier naturel défini par le fait d’avoir exactement deux diviseurs distincts, 1 et lui-même —, il existe une infinité de nombres de ce type, et leur répartition, qui ne semble être régie par aucune règle, paraît très irrégulière. Ces nombres sont particulièrement importants en arithmétique, la branche des mathématiques qui traite des nombres entiers. Mais ils font également l’objet d’une actualité brûlante dans les nouvelles technologies, en particulier dans la cryptographie, pour le codage des informations. Avec le développement d’internet, le besoin de transmettre des informations confidentielles de façon sécurisée, par exemple des numéros de carte bancaire, est en effet devenu primordial… C’est là notamment qu’intervient l’algorithme RSA, un algorithme de cryptographie basé sur une propriété simple des nombres premiers.

Principes de la cryptologie

La cryptologie, science du secret, englobe la cryptographie — le codage secret d’un message — et la cryptanalyse — le décodage d’un message codé. La cryptologie est une technique très ancienne. Ainsi, Jules César utilisait déjà un algorithme que nous appelons aujourd’hui le chiffrement par substitution, qui consiste à décaler d’une valeur constante les lettres dans l’ordre alphabétique. Mais la cryptologie est aussi une science qui se renouvelle. Depuis les années 1970, elle est devenue un thème de recherche scientifique académique.

Le principe de la cryptographie ? Définir une transformation des symboles d’un langage (les lettres ou les mots par exemple) qui soit difficilement inversible, de telle sorte que retrouver le mot original à partir du mot codé devienne une opération difficile à effectuer. Il existe deux grandes familles d’algorithmes de cryptographie : les algorithmes symétriques (à clé secrète) et les algorithmes asymétriques (à clé publique). La clé, en cryptographie symétrique, est l’information qui permet de coder (on dit aussi chiffrer) et de décoder un message. Ainsi, l’algorithme de décalage des caractères utilisé par Jules César est un algorithme à clé privée dont la clé est l’algorithme de codage : si l’on sait que les lettres utilisées ont été décalées d’une valeur constante (c’est-à-dire chaque lettre est remplacée par la n-ième lettre après dans l’ordre alphabétique, avec la convention de bouclage qui dit que la lettre suivant le z est le a) alors on sait aisément décoder le message. La machine Enigma qui fut utilisée par les Allemands durant la seconde guerre mondiale était également basée sur les substitutions, mais avec un mécanisme beaucoup plus sophistiqué.

Cryptographie à clé publique

Le principe de la cryptographie asymétrique (ou à clé publique) est basé sur l’existence d’une fonction dite à sens unique, pour transformer un message en message codé. Il faut que cette fonction soit simple à appliquer à un quelconque message, mais qu’il soit difficile de retrouver le message original à partir du message codé. La cryptographie à clé publique permet de coder un message secret et aussi d’authentifier l’émetteur d’un message.

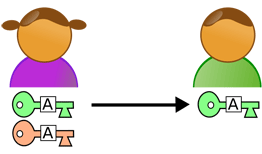
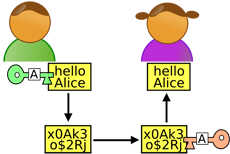
Principe de la cryptographie asymétrique. Alice génère deux clés : la clé publique (verte) qu’elle envoie à Bob et la clé privée (rose) qu’elle conserve précieusement sans la divulguer à quiconque.		Bob chiffre son message avec la clé publique d’Alice et lui envoie le texte chiffré. Alice déchiffre le message grâce à sa clé privée. Source : Wikipédia

Le principe est proche de celui d’un coffre à deux serrures. Lorsque l’une des deux serrures est fermée, la seule façon d’ouvrir la boîte est d’utiliser l’autre serrure. La clé d’une des deux serrures est publique, c’est-à-dire que tout le monde peut l’obtenir, tandis que l’autre est privée, et seule une personne la possède. Par exemple, admettons qu’un émetteur, appelé Bob en accord avec les conventions de l’analyse cryptographique, décide d’envoyer un message secret à Alice qui possède une telle boîte à deux serrures. Dans ce cas, Bob met dans la boîte d’Alice son message et referme la boîte avec la clé publique. Seule Alice pourra ouvrir la boîte, puisqu’elle est seule à posséder la clé privée. Elle seule pourra ainsi lire le message de Bob. Par ailleurs, pour signer un message, Alice le met dans la boîte qu’elle referme à l’aide de sa clé privée. Tous les destinataires pourront alors ouvrir le message, et seront certains que le message provient d’Alice, car elle est la seule à posséder la clé privée.

Le but de la cryptologie asymétrique est donc de construire un « coffre à deux serrures » virtuel. Nous allons étudier plus précisément un tel système, qui est très fréquemment utilisé et s’impose chaque année davantage dans le monde des communications informatiques. Il s’agit du système RSA, dont le principe est basé sur l’utilisation d’une propriété simple des nombres premiers.

Le système RSA

Inventé par Ron Rivest, Adi Shamir et Len Adleman, le système RSA (nommé d’après les initiales de ses auteurs) fut présenté pour la première fois en août 1977, dans la chronique mathématique de Martin Gardner de la revue Scientific American. Les circonstances de sa découverte sont assez amusantes : ces trois auteurs avaient décidé de travailler ensemble pour démontrer l’impossibilité logique des systèmes cryptographiques « à clé publique ». Ils échouèrent donc en découvrant un système de cryptographie à clé publique, le système RSA. Mais cet échec n’en est pas vraiment un : l’efficacité du système RSA à clé publique est depuis lors reconnue et a assuré la renommée de ses auteurs !

Le système RSA est aujourd’hui un système universel servant dans une multitude d’applications. Sa technique est protégée par un brevet dans certains pays (aux Etats-Unis, ce brevet a expiré en septembre 2000). Elle a été vendue à près de 350 entreprises et on estime que plus de 300 millions de programmes installés peuvent utiliser le RSA, les transactions sécurisées via internet par exemple l’emploient pour la plupart. Internet fait un usage systématique du RSA pour assurer la confidentialité du courrier électronique et authentifier les utilisateurs.

Le coin des matheux

Le protocole RSA est fondé sur un résultat d’arithmétique dont la démonstration prend quelques lignes. Mais prenons d’abord le temps de définir quelques notions importantes sur les nombres entiers. Rappelons qu’un nombre premier n’est divisible que par lui-même et par un. Il en existe une infinité, {2, 3, 5, 7, 11, 13, 17, 19, 23, 29…}. Ces nombres sont d’une importance particulière dans l’étude des nombres entiers, notamment par le fait que chaque nombre entier s’écrit de façon unique (à l’ordre des facteurs près) comme un produit de nombres premiers.

On dit que p est un diviseur du nombre entier n s’il existe un nombre entier q tel que n = p × q. Deux nombres entiers p et q sont dits premiers entre eux si le plus grand entier divisant à la fois p et q est 1. Dans ce cas, le théorème de Bezout nous assure qu’il existe deux nombres entiers relatifs (l’un positif, l’autre négatif) m et n tels que m × p + n × q = 1. Forts de ces résultats, énonçons la propriété fondamentale du fonctionnement du RSA.

Théorème. Soient p et q deux nombres premiers, et posons n = p × q.
Soit e est un entier premier avec (p – 1) × (q – 1), alors il existe un entier d > 0 et un entier m tels que e × d + m × (p – 1)(q – 1) = 1.
Notons au passage que si on choisit d positif et inférieur à (p – 1)(q – 1), alors d est unique.

On note a^k le nombre a élevé à la puissance k, c’est-à-dire le nombre a multiplié par lui-même k-1 fois.

Pour tout entier a < n premier avec n, le reste de la division de a^e×d par n est égal à a.

Démonstration

Le reste de la division de x par n vaut y s’exprime en langage mathématique : x est congruent à y modulo n et se note x ≡ y [n]. Cette notation est utilisée dans la suite de ce document. On appelle φ la fonction indicatrice d’Euler, c’est-à-dire la fonction qui associe à tout entier naturel n le nombre de nombres premiers avec n dans l’ensemble {1, . . . , n}. Pour un nombre premier p, on a φ(p) = p – 1 car seuls 1 et p ne sont pas premiers avec p dans l’intervalle {1, . . . , n}. D’autre part, on a φ(p×q) = (p – 1) × (q – 1) pour p et q deux nombres premiers distincts. En effet, les seuls nombres entiers compris entre 1 et p×q qui ne sont pas premiers avec p×q sont les multiples de p ou de q. Il y a exactement p multiples de q dans {1, . . . , p×q} et q multiples de p. L’entier p×q est à la fois multiple de p et de q, donc on a p + q – 1 diviseurs de p×q distincts dans l’ensemble {1, . . . , p×q}, donc φ(p×q) = p×q – p – q  + 1 = (p – 1)(q – 1).

Le petit théorème de Fermat généralisé nous assure que pour tout entier a premier avec un entier n, on a : a^φ(n) ≡ 1 [n].

Comme e est supposé premier avec (p – 1)(q – 1), on sait d’après le théorème de Bezout qu’il existe un entier d tel que e × d = 1  + m × (p – 1)(q – 1). Soit a un nombre premier avec p×q. On a
a^ed = a^{1 + m×(p – 1)(q – 1)}
= a × (a^φ(p×q))^m
≡ a×1^m [p×q]
≡ a
en utilisant le petit théorème de Fermat généralisé.

De ce théorème, on déduit alors le protocole RSA pour le codage.

Protocole RSA pour le codage

On suppose qu’Alice doit recevoir des messages cryptés. D’après le théorème précédent, voici quelle sera la procédure qu’elle pourra suivre :

• Elle calcule deux nombres premiers p et q, choisit e un nombre premier avec (p – 1)(q – 1) et d tel qu’il est défini dans le théorème, c’est-à-dire tel qu’il existe un nombre entier relatif m tel que :
  e × d + m × (p – 1)(q – 1) = 1Pour ce faire, elle peut utiliser un algorithme de calcul très connu depuis l’Antiquité (vers 300 ans avant Jésus-Christ) appelé algorithme d’Euclide.Elle calcule également n = p × q.
• Alice rend publics les nombres n et e (par exemple en les publiant dans un annuaire, sur un site internet ou bien en les communicant directement à l’expéditeur, Bob). Elle conserve secrètement et bien cachés les nombres p, q et d, et peut même détruire p et q car ils ne serviront plus à personne.
• Bob, qui veut transmettre une information secrète à Alice, transforme son information en un nombre entier A inférieur à n (ou en plusieurs nombres si nécessaire) avec un codage connu de tous.
• Bob élève ensuite A à la puissance e, et prend le reste de la division du nombre qu’il a obtenu, A^e, par le nombre n que lui a également fourni Alice. Il envoie ce reste, que nous notons B, de façon non protégée.
• Alice élève alors le nombre B que Bob vient de lui envoyer à la puissance d, qui est sa clé secrète, et obtient en prenant le reste de la division de B^d par n, par application du théorème du RSA, le message original que Bob lui a envoyé (car B^d ≡ (A^e)^d [n] ≡ A^ed[n] ≡ A [n] d’après le théorème du RSA).

Ainsi, la clé publique est constituée par les nombres e et n. Bob, s’il veut coder un message, le transforme en fermant la serrure publique. Fermer la serrure publique consiste tout simplement à élever le message (transformé en un ou plusieurs nombres entiers inférieurs à n) à la puissance e et à en prendre le reste par la division par n. Une fois cette opération effectuée, le message n’est plus compréhensible. La seule façon de retourner au message initial est de posséder la clé privée d. Pour obtenir le message original et ouvrir la serrure privée, il s’agit simplement d’élever le message obtenu à la puissance d et de prendre le reste de ce résultat par la division par n. Le protocole symétrique permettra à Alice d’authentifier un message. On a donc bien créé un « coffre à deux serrures » virtuel !

Exemples d’utilisation du RSA

Tout d’abord, un exemple trivial qui vous permettra de vérifier le fonctionnement de ce système même si vous n’avez pas de calculatrice sous la main.
Prenons par exemple les nombres p = 3 et q = 5. Nous calculons alors n = p×q = 15 et (p-1)×(q-1) = 8. Dans ce cas, e = 3 est premier avec 8. On peut choisir d = 3 puisque e×d = 3×3 = 9 = 8×1 + 1.
Soit enfin le nombre à coder A = 2. Nous avons A^e = 2³ = 8, donc A^e est congruent à 8 modulo 15. Le nombre codé est donc B = 8.
Pour décoder, nous prenons le reste de la division de B^d par n. B^d = 8³ = 512. En faisant la division euclidienne de 512 par 15, nous obtenons : B^d = 512 = 34×15 + 2. Le reste est donc 2, c’est-à-dire A, le nombre que nous avons codé au départ.

Imaginons maintenant un exemple un peu plus complexe. L’auteur de ce document, adepte du chiffrement RSA, sait qu’il doit recevoir de la part de ses lecteurs des messages hautement confidentiels d’une grande importance. Il choisit d’utiliser le système RSA, et génère deux nombres premiers, p = 17 et q = 11. Il choisit également le nombre e = 7 qui est premier avec (p – 1) (q – 1) = 160. Il calcule à partir de ce nombre e sa clé privée qu’il ne divulguera jamais. Pour ce faire, il doit chercher un nombre d tel qu’il existe un entier m tels que ed +  m (p – 1) (q – 1) = 1. Il décide de le faire par tâtonnement plutôt que d’utiliser l’algorithme d’Euclide, et cherche le plus petit m > 0 tel que m (p-1) (q-1) +  1 soit divisible par e = 7. Pour m = 1, il observe que m (p – 1) (q – 1) + 1 = 161 = 7 × 23. Sa clé privée ultra-secrète sera donc d = 23.

L’auteur rend aussi publique une correspondance entre lettres et chiffres afin de coder des messages textuels, et choisit la convention suivante :

L’espace entre deux mots sera codé par 00. L’auteur envoie donc à tous ses honorables correspondants la clé (n = 187, e = 7), appelée clé publique et garde pour lui seul, bien caché, le nombre d = 23, appelé clé privée.

Un des lecteurs de ce document, appelons-le Bob, décide de communiquer un message ultra-secret à l’auteur : « les maths, c’est génial ! ». Bob va donc coder ce message avec la clé publique (n, e). Pour commencer, il convertit les lettres en chiffres, en utilisant la correspondance convenue, et obtient ainsi le nombre :
1205190013012008190003410519200007051409011240

Il regroupe ce nombre en tranches de chiffres strictement inférieurs à n = 187 :
120 51 90 013 012 008 19 000 34 105 19 20 000 70 51 40 90 112 40

Chacun de ces nombres inférieurs à n sera codé en utilisant la clé privée. Il s’agit donc pour Bob d’élever chaque nombre à la puissance 7 et d’en prendre le reste par la division par 187. Il utilise pour cela une calculatrice ou un ordinateur, afin de gagner du temps. Il note chaque mot codé en ajoutant des zéros à gauche afin que chaque nombre soit composé de trois chiffres et il obtient le code :
120017095106177134145000034096145147000060017116095073116
C’est ce message codé qu’il envoie à l’auteur du document.

Toute personne recevant ce message est incapable de retrouver le message original envoyé par Bob, s’il ne connaît pas la clé secrète. Néanmoins, l’auteur, lui, possède la clé secrète d = 23. Pour décoder le message, il lui suffit de découper le message en tranches de nombres à trois chiffres, de prendre chaque nombre de cette décomposition, de l’élever à la puissance d puis de diviser le résultat par n et de noter le reste obtenu. Il va alors retrouver 120 pour 177, 51 pour 146, et ainsi de suite. L’auteur va ainsi obtenir le message non codé. Il ne lui reste plus qu’à prendre son tableau de correspondance alphabétique pour retrouver le message original « les maths, c’est génial ! ».

Bien entendu, codage et décodage se font sur ordinateur, en raison de la longueur des opérations. Mais si le reste de la division d’un nombre par un autre peut se calculer informatiquement de façon très efficace en utilisant l’algorithme d’Euclide, et que le temps de calcul est linéaire en fonction du nombre de chiffres du nombre à diviser, il n’en est pas de même pour le problème de la factorisation d’un nombre (c’est-à-dire le problème de décomposer ce nombre en produit de facteurs premiers). Il n’existe pas de méthode connue pour le diviser en temps polynomial, c’est-à-dire dont le temps de calcul croîtrait comme une puissance de la taille du nombre à factoriser. Supposons donc maintenant qu’un ennemi de l’auteur aimerait bien connaître le message envoyé par Bob. Il connaît la clé publique (n = 187, e = 7), il ne peut cependant pas décrypter le message car il lui faudrait avoir la clé secrète d = 23. Pour l’obtenir, il doit décomposer n en facteurs premiers, ce qui est certes facile avec 187, mais impossible actuellement — à moins d’y consacrer des siècles et des milliers d’ordinateurs ou de recourir à la divination — avec un nombre de 150 à 200 chiffres.

Animation interactive

Nous vous proposons une animation pour tester la génération de clés ainsi que le codage et le décodage des messages. La conversion des lettres en nombres s’y fait un peu différemment de l’exemple précédent, mais la génération et l’utilisation des clés sont semblables.

Sécurité du RSA

La sécurité de l’algorithme RSA repose sur deux conjectures. La première, considérer que pour casser le RSA et donc découvrir la clé privée, il faut factoriser le nombre n. La deuxième est de considérer que la factorisation est un problème difficile, c’est-à-dire qu’il n’existe pas d’algorithme rapide (de complexité polynomiale) pour résoudre cette question. Aucune de ces deux conjectures n’est prouvée. Il se peut donc que les deux soient fausses. Si c’est effectivement le cas, alors RSA n’est pas un algorithme de cryptographie sûr.

La génération de quadruplets (p, q, e, d) avec des nombres premiers p et q de quelques dizaines ou centaines de chiffres est une tâche facile et rapide, ce qui est essentiel pour une utilisation réelle du système cryptographique. On obtient sans peine des nombres premiers de cette taille par des algorithmes probabilistes de primalité. On peut ensuite choisir e au hasard et vérifier si le nombre obtenu est premier avec (p – 1) (q – 1), ce qui est une opération facile et rapide en utilisant l’algorithme d’Euclide qui fournit dans le cas où e est premier avec (p – 1) (q – 1) la clé privée d en même temps. Avec les techniques utilisées aujourd’hui pour programmer les systèmes RSA, on estime que le doublement de la longueur des clés multiplie le temps de génération des clés par 16 et le temps de codage et décodage par 4.

L’usage du système RSA est donc dit polynomial : le temps de calcul se comporte comme un polynôme de la longueur de la clé ; en revanche, on fait l’hypothèse que casser le RSA nécessiterait des algorithmes bien plus longs que polynomiaux. Certains en déduisent que plus les machines seront puissantes, plus l’écart se creusera entre la puissance de calcul disponible mise en œuvre pour créer et utiliser des clés plus longues et la puissance requise pour casser le RSA. Autrement dit, plus le temps passe, plus le RSA devient robuste et sûr. La confiance dans la sécurité du système RSA ne repose pas sur une démonstration. Elle vient plutôt de l’échec répété depuis plus de 25 ans de toutes les tentatives pour casser ce système.

Nouveaux angles d’attaque

Sur le plan théorique, la situation est décevante et le restera longtemps encore. Dès que l’on sait factoriser n en p×q, on trouve immédiatement d. Si on connaît n, e et d, on peut trouver rapidement p et q. Cependant, les difficultés pour casser le RSA ne sont pas nécessairement liées à la factorisation de n, il est probable que l’on puisse casser le RSA sans passer par des factorisations. Des arguments proposés récemment indiquent même que ce type d’attaque doit être sérieusement envisagé : en 1998, Dan Boneh, de l’université de Stanford, et Ramarathnam Venkatesan, de la société Microsoft, ont établi que pour des exposants e petits, casser le RSA n’est pas équivalent à factoriser n.

Une autre attaque très astucieuse du RSA, proposée par Paul Kocher, consiste à mesurer minutieusement le temps mis par des cartes à puce pour décrypter les messages qu’on leur soumet, et à exploiter ces résultats pour retrouver la clé secrète. Mais on se prémunit aisément de cette attaque en faussant le temps de calcul apparent en attendant un certain temps (variable) à la fin du décodage.

Enfin, en 1994, Peter Shor a montré qu’avec un ordinateur quantique, on peut factoriser très efficacement les nombres entiers (en un temps proportionnel à la longueur de la clé).

Même si aujourd’hui l’ordinateur quantique est encore du domaine de la fiction, sa mise au point étant estimée à quelques décennies, l’avancée de certains services spéciaux n’est pas à exclure. Finalement, les cassages déjà réalisés du RSA sont tous liés à des faiblesses dans la mise en œuvre et non à l’attaque du noyau mathématique. Il ne s’agit là que d’observations pratiques tirées du constat que toutes les tentatives répertoriées d’attaque du RSA échouent quand les conditions de sécurité sont respectées. Ce constat n’interdit pas de penser que le risque théorique lié au RSA est grand puisque l’on ne sait pas démontrer la difficulté de la factorisation d’un nombre, ni même qu’il faut passer par la factorisation pour casser le RSA.

Plusieurs fois dans l’histoire de l’espionnage, un système de codage a été considéré comme inviolable par ses utilisateurs alors qu’un service ennemi lisait tranquillement tous les messages qui tombaient entre ses mains. Ainsi, pendant la première guerre mondiale, les services français décodaient les messages destinés aux sous-marins allemands et agissaient en conséquence. Pendant la seconde guerre mondiale, le code de la célèbre machine allemande Enigma a été craqué. Or les centaines de personnes ayant participé à ce décryptage sont restées muettes pendant plus de 30 ans. On sait aujourd’hui que des agences de renseignement puissantes consacrent des moyens considérables au décryptage du RSA. On doit donc envisager sérieusement le risque que des spécialistes, quelque part, connaissent une façon de casser le RSA et se taisent. En l’absence de résultat prouvant mathématiquement la sécurité du RSA, comme de bien d’autres méthodes de cryptage, il est sage de ne pas faire trop confiance à ces méthodes et de combiner les systèmes admis comme sûrs.

Animation HTML5/JS réalisée par Ouest INSA, adaptée de l’applet proposée par Roger Morrison.