Commander les robots

1. Quelle commande pour quels robots ?

Commander un robot, fort modestement, consiste ici à s’intéresser à la seule exécution des consignes (notion que nous préciserons par la suite), c’est-à-dire sans faire référence à une quelconque intelligence ou autonomie décisionnelle du robot.

Mais le monde des robots est peuplé de nombreuses espèces qui diffèrent par leur taille (du nano-robot à l’engin de chantier), leur structure, et donc par les mouvements qu’ils sont susceptibles d’effectuer, par exemple pour se déplacer. Ainsi, un robot mobile à roues ou à chenilles ne se pilotera pas de la même façon qu’un hexapode, un quadrupède ou un humanoïde.

Si, comme dans la nature, le problème de la locomotion des robots a donné lieu à des solutions conceptuellement extrêmement différentes, le mouvement des bras chez les robots s’effectue au contraire à l’aide d’un petit nombre de structures mécaniques articulées généralement assez semblables. C’est pourquoi nous nous intéresserons exclusivement à celles-ci au cours de ce petit voyage dans le monde de l’automatique, périple qui nous permettra d’admirer au passage quelques jolis paysages dans les domaines de la géométrie, de la mécanique classique et des équations différentielles.

Bouger les bras

Il existe différentes raisons qui nous font exécuter des mouvements avec les bras, de façon volontaire ou non : par exemple s’équilibrer en marchant, faire des signes de la main, attraper un ballon, se protéger d’une chute, écrire, jouer d’un instrument… La dextérité, la force, la précision, la vitesse requises sont à chaque fois différentes, et, pourtant, ce sont les mêmes dispositifs qui sont utilisés à chaque fois : bras et mains, affublés parfois d’un « outil » externe supplémentaire, et cela, avec une admirable et optimale utilisation des ressources disponibles, muscles, squelette et sens.

La commande d’un bras de robot, même si ce dernier est moins mobile qu’un bras humain, sera soumise au même impératif : comment utiliser au mieux un dispositif donné pour réaliser des tâches suffisamment variées ? Dans le cas d’un robot, ce problème sera résolu simplement en tentant de séparer explicitement les deux aspects : d’une part, spécifier une « tâche » à effectuer dans un espace adéquat, et d’autre part, faire bouger un système mécanique articulé en connaissant ses propriétés dynamiques. Commençons donc par ce dernier aspect.

Qu’est-ce qu’un bras de robot ?

Robot RX90 Stäubli. © INRIA / Photo A. Eidelman

Sur le plan technologique, un bras de robot classique est constitué d’un assemblage de segments reliés par des articulations, elles-mêmes généralement motorisées. Les robots industriels (parfois appelés bras manipulateurs) distinguent souvent la partie « porteur », qui réalise de grands déplacements dans l’espace, de la partie « organe terminal », constituée de préhenseurs ou d’outils amovibles, installés sur un poignet articulé.

Les liaisons sont des articulations soit rotoïdes (elles permettent d’effectuer un mouvement de rotation autour d’un axe), soit prismatiques (elles permettent un mouvement de translation le long d’un axe). Les « muscles » du robot, ses actionneurs, utilisent une énergie électrique, hydraulique ou pneumatique, et les forces et mouvements produits par les moteurs sont transmis aux articulations par divers dispositifs : réducteurs à engrenages, vis à billes, bielles, courroies ou tout autre système issu de l’imagination fertile des concepteurs.

Dans la terminologie de la mécanique, un bras de robot constitue une chaîne cinématique, qui peut être simple (les articulations se suivent une à une, comme dans le bras humain), ou arborescente (il existe des branches indépendantes, comme les doigts dans une main), ou même présenter des boucles, c’est-à-dire des sous-ensembles mécaniques refermés sur eux-mêmes (comme c’est le cas pour ma lampe de bureau).

Mais quelle que soit l’architecture considérée, et avant même de vouloir faire bouger ce robot, il importe de savoir comment le repérer, c’est-à-dire caractériser d’une manière géométrique sa position et sa relation à la tâche à accomplir. Et ce n’est pas aussi simple que l’on pourrait le croire.

Ainsi, lorsque je me penche pour ramasser la pomme que je viens de faire tomber, mon corps adopte une certaine forme, la « posture », qui est la solution d’un calcul d’optimisation réalisé implicitement par mon système nerveux. Et si je suis perclus de rhumatismes, la posture adoptée sera certainement différente de celle choisie si je suis champion de France de gymnastique, alors que la tâche effectuée est identique. Ceci montre qu’en l’espèce, il existe plusieurs solutions au problème posé. Il apparaît ainsi à nouveau la nécessité de séparer la spécification de ce problème de sa résolution par un système robotique.

Une question de configuration

Intéressons-nous donc en premier lieu à la question de la posture. Pour un robot, la posture sera appelée « configuration ». Qu’est-ce donc que la configuration ? D’une façon générale, la configuration d’un système est la valeur de ses paramètres de position, et l’espace de configuration (noté E_c) est l’ensemble des positions possibles dudit système.

Nous voilà assez peu avancés avec cette définition ! Prenons plutôt quelques exemples :

• Soit un point matériel dans l’espace. Sa position dans un repère fixe est donnée par 3 coordonnées, par exemple, si l’on utilise un GPS, la latitude, la longitude et l’altitude. Son espace de configuration théorique est donc l’espace tridimensionnel, appelé ℜ³ (facile : ℜ pour indiquer un nombre réel et 3 pour la dimension !).
• Prenez la souris sans fil de votre ordinateur. D’abord, pour ce qui est du spot sur l’écran, c’est simple : si l’écran est plat et en faisant abstraction de la résolution, sa position peut être repérée par deux valeurs : par exemple, sa distance horizontale par rapport au bord gauche de l’écran et sa distance verticale par rapport au bord inférieur ; son E_c est donc de dimension 2 et n’est autre que ℜ² ; mais comme le spot ne peut pas sortir de l’écran, cet E_c est en fait un sous-ensemble de ℜ².
  Et la souris elle-même ? Si l’on oublie un instant sa fonction de souris, il s’agit d’un objet rigide potentiellement libre dans l’espace, un peu comme un avion. Donc son E_c (de même que celui de l’avion) comporte deux parties : la position, comme pour le point matériel, soit ℜ³, et, ce qui est nouveau, l’orientation. Celle-ci comporte trois dimensions de rotation, qui peuvent être nommées par exemple, pour reprendre l’image aéronautique, le roulis, le tangage et le lacet. L’espace associé est noté par les mathématiciens SO(3).Pour le lecteur qui n’a pas le mal de mer, on résumera l’espace de configuration complet d’un objet physique capable de se déplacer et de s’orienter librement dans l’espace par la formule : E_c = ℜ³ × SO(3), soit une dimension 6 au total.
  Bon, mais la souris vole mal, et sa vocation est de se promener sur un tapis, dit de souris, justement… Son mouvement est donc restreint par le fait qu’elle doit rester dans le morceau de plan que constitue le tapis. Son espace de travail réel est de ce fait une portion de ℜ², mais que l’on peut voir maintenant comme un sous-espace de ℜ³ × SO(3) (une souris libre comme l’air) défini par les contraintes de sa fonction de souris (reste sur le tapis !).
• Finalement, dans le cas d’un bras de robot, on a affaire à une suite de corps, chacun avec au départ un espace de configuration propre de dimension 6, les contraintes réduisant ces espaces étant cette fois engendrées par les articulations qui relient les corps.
  Un exemple illustre cela dans la vidéo ci-dessous.

Faites l’expérience : construisez un bras articulé.
Durée : 2 min 18 s.

Résumons-nous à présent. Un bras articulé de robot, s’il doit positionner et orienter un corps dans l’espace, doit avoir six degrés de liberté actionnés. S’il est fixé au sol, il devra donc avoir au moins six articulations. Pour la suite, nous supposerons donc que notre bras de robot type a six articulations actionnées, disposées de façon à atteindre un sous-ensemble de ℜ³ × SO(3) qui est son espace de travail, limité par la structure du robot. Cet espace est de dimension 6 (on aura généralement trois articulations dédiées au positionnement de l’organe terminal et trois à son orientation).

Mais comment, en pratique, repérer son espace de configuration, en choisir les paramètres ? En fait, il suffit de choisir n’importe quel ensemble de six variables indépendantes liées au système ! Le plus simple consiste à choisir directement les coordonnées articulaires, qui seront donc nos six variables à commander, et de les rassembler dans un vecteur noté q.

2. Ca y est, on va le faire bouger

Lorsque l’on pose la main sur la souris, on lui applique en fait des forces qui vont permettre son déplacement. L’étude du mouvement des corps soumis à des forces aussi diverses que la pesanteur ou l’action d’un moteur s’appelle la dynamique. Choisir les forces à appliquer pour obtenir le mouvement que l’on souhaite, tout en tenant compte du mouvement réel que l’on observe, est un problème de commande. C’est ce que nous allons à présent étudier, dans le cas particulier où le système mécanique n’est autre que notre bras de robot.

Le pendule de Tournesol

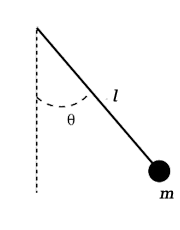
Schéma du pendule de Tournesol.

À ce stade, il était nécessaire de convoquer une éminente personnalité scientifique pour nous expliquer quelques rudiments de dynamique et de commande. Nous avons eu la chance de rencontrer le célèbre Professeur Tournesol, au moment où il travaillait sur son fameux pendule. Voici un verbatim de notre entretien.

Professeur Tournesol : Un peu plus à l’ouest…

Interstices : Professeur, pouvez-vous nous parler de la dynamique de votre pendule ?

Professeur Tournesol : De la dynamite, où ça ?

Interstices : De la DYNAMIQUE !

Professeur Tournesol : Ah oui… Eh bien voyez-vous, si je ne bouge pas la main, et en assimilant le fil à une tige rigide sans masse de longueur l, mon pendule est en quelque sorte un système à deux rotations, dont l’extrémité (une masse ponctuelle de valeur m) se déplace sur une portion de sphère. Mais pour simplifier, je vais en bloquer une et le laisser osciller dans un plan vertical. Son mouvement résultera alors de l’action de mon fluide magnétique personnel…

Interstices : Professeur, je vous en prie…

Professeur Tournesol : Bon, oublions cela. Mon pendule, qui est à présent un système à une dimension, repéré par l’angle (\theta\) [theta] de sa tige avec la verticale, est soumis à plusieurs forces, dont essentiellement la pesanteur et l’inertie. L’équation de son mouvement ressemble à la fameuse équation \(F – m \gamma = 0\) [\(F\) moins \(m\) gamma égale zéro], qui exprime que l’accélération \(\gamma\) [gamma] d’un corps de masse \(m\) est d’autant plus élevée que la force \(F\) qu’on lui applique est importante. Je dirais même plus, l’équation du mouvement du pendule est [il sort de je ne sais où un bout de papier chiffonné et un minuscule crayon, puis griffonne à toute vitesse en marmonnant] :

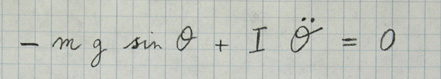
[moins \(mg\) sinus de theta plus \(I\) dérivée seconde de theta égale zéro].

Interstices : ? ? ?

Professeur Tournesol : Quelle tête vous faites ! On dirait le capitaine Haddock devant une bouteille d’eau minérale… Bon, je vais essayer de vous expliquer. Dans le cas de mon pendule, quelle est la force appliquée \(F\) ? C’est juste la pesanteur, qui fait tomber la boule, puisque vous refusez d’admettre la puissance de mon fluide. Et vous voyez bien que si le pendule que je tiens est vertical, celle-ci est nulle, alors qu’elle est maximale à l’horizontale : d’où \(F=-mg \sin \theta\) , où \(m\) est la masse de la boule et \(g\) l’accélération de la pesanteur, égale à 9,81 m/s², \(mg\) étant alors tout simplement son poids. Quant à l’accélération, le seul mouvement présent est la rotation, définie par l’angle \(\theta\). C’est donc l’accélération de celle-ci qui est considérée, c’est-à-dire sa dérivée seconde, qu’on note \(\theta\) surmonté de deux points, la dérivée première étant la vitesse, qu’on note \(\theta\) surmonté d’un point.
Et pour finir, rappelez-vous que, quand on tourne, c’est l’inertie qui compte, et non la masse seule… C’est ce que j’appelle \(I\), qui dépend d’ailleurs de la masse de la boule et de la longueur du fil, elle vaut ici \(ml^2\).
Et le tout s’appelle une équation différentielle, c’est-à-dire une équation dont l’inconnue n’est pas une valeur mais une fonction – c’est l’angle de rotation qui varie – et dont les termes font intervenir les dérivées de la fonction. Ici, elle est du deuxième ordre, car comme je l’ai dit, elle implique une dérivée seconde, l’accélération.

Interstices : Bien. À présent, j’ai un moteur, et je voudrais positionner le pendule à un angle donné \(\theta_d\) [theta indice d]. Comment faire ?

Professeur Tournesol : En fer ? Non, plutôt en alliage, c’est plus léger.

Interstices : COMMENT MOTORISER LE PENDULE ?

Professeur Tournesol : Oui, oui, j’ai compris, je ne suis pas sourd… Installons donc votre moteur sur l’axe, et supposons qu’il soit capable de fournir un couple \(C\). Nous voulons donc positionner notre pendule à l’angle \(\theta_d\), c’est notre consigne. Alors c’est tout simple, il suffit de trouver le « bon » couple \(C\).

Interstices : Ben voyons… Et où le trouve-t-on ce « bon couple »? Un peu plus à l’ouest ?

Professeur Tournesol : Pas exactement. En fait, utiliser un moteur revient à ajouter une force extérieure \(C\) à la pesanteur, et la dynamique du pendule est à présent [il modifie la formule sur son papier] :

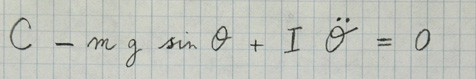
[\(C\) moins \(mg\) sinus de theta plus \(I\) dérivée seconde de theta égale zéro].

En regardant le pendule, on devine bien que, d’abord, le couple doit être positif si \(\theta\) est plus petit que \(\theta_d\) et négatif dans le cas contraire, juste histoire de tourner dans le bon sens. Et l’on a envie de corriger d’autant plus fortement que l’écart sera important. Donc, on introduit un coefficient \(k_p\) positif qui « règle » l’ampleur de la correction, et on obtient un truc du genre \(C=\k_p (\theta_d -\theta)\)
[\(C\) égale moins \(k\) indice p facteur de theta indice d moins theta].

Interstices : C’est tout ?

Professeur Tournesol : Ah, cette toux ? Oui, j’ai un peu pris froid. Mais pourquoi changez-vous sans cesse de sujet ? Ce n’est pas fini : si on en reste là, le pendule va dépasser \(\theta_d\), puis revenir en arrière, et ainsi de suite… et cela n’en finira jamais. On va donc ajouter un machin pour le freiner : c’est un terme qui dépend de la vitesse (dérivée de l’angle), et dont l’intensité de l’action est réglée par un autre coefficient, le coefficient positif \(k_v\), appelé « coefficient d’amortissement ». Ce qui freine, c’est donc le produit de ce coefficent d’amortissement \(k_v\) et de la vitesse angulaire dérivée de \(\theta\). Et finalement le couple de commande à appliquer est calculé ainsi
[il reprend son papier, saisit son crayon et ajoute en dessous de l’équation précédente] :

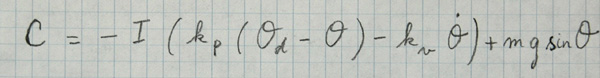
[\(C\) égale moins \(I\) facteur de entre parenthèses \(k\) indice p facteur de entre parenthèses theta indice d moins theta fermer la parenthèse moins \(k\) indice v dérivée de theta fermer la parenthèse plus \(mg\) sinus de theta]

Interstices : Euh, attendez… je retrouve bien le truc – \((k_p (\theta_d – \theta))\), le machin \(k_v\) dérivée de \(theta\), mais vous avez aussi rajouté des choses bizarres…

Professeur Tournesol : Eh bien quoi ? C’est évident, non ? Le dernier terme, dans l’expression du couple calculé \(C\) qui constitue la commande, permet d’annuler l’effet de la pesanteur dans cette expression, c’est-à-dire le poids de la boule ; c’est en quelque sorte une pesanteur inversée ! Quant à l’introduction de l’inertie \(I\) dans la commande, elle permet d’avoir également un comportement indépendant de la valeur de \(I\). Avec cette commande, vous remplacez ma boule en acier par une bille de plastique, ça ne change rien du tout.

Et, finalement, en appliquant la commande donnée par la première équation au système donné par cette deuxième équation, on obtient ce que l’on appelle un système bouclé, dont l’équation se réduit à [et il ajoute une troisième ligne de pattes de mouche] :

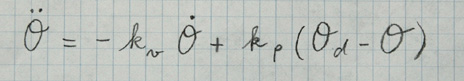
[dérivée seconde de theta égale moins \(k\) indice v dérivée de theta plus \(k\) indice p facteur de theta indice d moins theta]

Interstices : Et alors ? Rien ne prouve que ça marche, votre affaire !

Professeur Tournesol : Mais il faut tout vous dire ! Il s’agit, là encore, d’un magnifique spécimen d’équation différentielle linéaire du second degré. Je vais vous expliquer ce qu’elle signifie, c’est-à-dire vous montrer que le pendule va se comporter comme nous l’avons prévu en choisissant notre commande.
Grâce à cette équation, l’angle \(\theta\) va évoluer vers \(\theta _d\) d’une façon bien déterminée. Oublions tout d’abord provisoirement le terme en vitesse dérivée de \(\theta\). On voit que l’accélération dérivée seconde de \(\theta\) sera proportionnelle à l’écart entre la valeur instantanée et la valeur désirée de l’angle : plus on sera loin, plus on va accélérer pour s’approcher de la valeur cible, et inversement.
Supposons maintenant que l’on soit très près de cette valeur désirée. Alors, on peut oublier un moment à son tour le terme \((\theta_d – \theta)\) qui est petit, et s’intéresser au terme \(-k_v\) dérivée de \(\theta\). L’accélération dépend donc de la vitesse à laquelle on se trouve. Si celle-ci est grande et dans le bon sens, alors on va freiner fortement, comme lorsque l’on arrive trop vite à un péage autoroutier.
Inversement, si la vitesse est grande et dans le mauvais sens (c’est-à-dire tendant à éloigner l’angle de sa valeur désirée), alors on accélère très vivement pour la remettre dans le bon sens. Comme je vous l’ai déjà dit, tout ceci se « règle » en modifiant les paramètres positifs \(k_p\) et \(k_v\), que l’on appelle les gains de l’asservissement. Et finalement, comme disent les professionnels, nous avons ainsi réalisé ici une commande proportionnelle dérivée avec, de plus, une compensation de la dynamique du pendule qui marche bien grâce aux termes \(I\) et \(-mg \sin \theta\) de la commande.

Interstices : Mais…

Professeur Tournesol : Bien évidemment, ceci suppose que nous soyons capables de mesurer l’angle \(\theta\) et la vitesse angulaire dérivée de \(\theta\) de notre pendule. Il faut donc disposer de capteurs, par exemple intégrés dans les moto-réducteurs.

Interstices : Les motos ?

Professeur Tournesol : Un moto-réducteur, c’est un moteur particulier, avec des engrenages intégrés pour mieux démultiplier sa force et contrôler la position ou l’orientation d’un degré de liberté…

Interstices : Merci Professeur. Et je suppose que tout ceci se généralise très bien à des systèmes articulés plus complexes ?

Professeur Tournesol : Bien sûr que non, ceci se généralise très bien à des systèmes articulés plus complexes, et d’ailleurs à toutes sortes de systèmes comme le contrôle de la température avec un thermostat ou celui du niveau d’eau dans un réservoir. Cela s’appelle de l’automatique. Bon maintenant rendez-moi mon pendule.
Un peu plus à l’ouest…

Il ne fut pas possible de tirer plus du Professeur. Mais nous avons gardé précieusement ses formules.

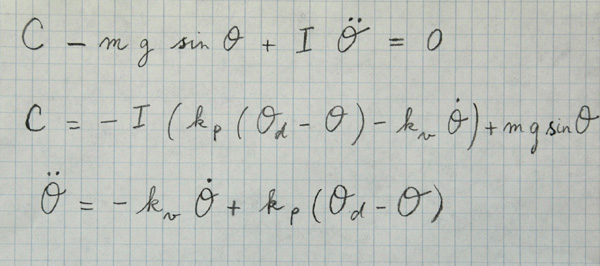
Et les chercheurs en automatique et en robotique confirment qu’effectivement, la démarche peut se généraliser à des chaînes cinématiques comme celles constituant un bras de robot. En voici un aperçu.

Dynamique et commande articulaires

C’est à Joseph-Louis Lagrange que sont dues les équations qui en robotique permettent d’obtenir explicitement le modèle dynamique, multidimensionnel, d’un bras articulé. Après Isaac Newton, et avec son contemporain Leonhard Euler, ce grand mathématicien, né à Turin en 1736 et mort à Paris en 1813, a, entre autres, inventé la mécanique analytique.

Le modèle basé sur les équations de Lagrange peut être vu comme une généralisation de la formule classique de la dynamique déjà citée \(F-m\gamma = 0\). Pour l’illustrer, imaginons que l’on assemble bout à bout \(n\) pendules rigides du type Tournesol modifié Interstices ®. Et si l’on essayait, en première approche, d’empiler les modèles de chacun (selon l’équation déjà évoquée, avec cette fois un indice \(i\) pour chacun) pour obtenir le modèle du tout ?

Allons-y : on rassemble les couples de commande \(C_i\) dans un vecteur \(\Gamma\), les angles \(\theta_i\) dans un vecteur de positions articulaires \(\mathbf{q}\), les poids \(m_i g\) dans un vecteur \(G\) et les inerties \(I_i\) dans un terme \(M\).

On aurait alors envie d’écrire la forme générale :
\(\Gamma – M \ddot{\mathbf{q}} + G = 0\).

Voilà, M’sieur, est-ce que j’ai bon ?

Il y a de l’idée, cher lecteur, mais malheureusement, ce n’est pas si simple, ne serait-ce que par exemple en raison des effets de couplage : si vous secouez l’un des pendules, tous les autres vont se mettre à bouger, et ceci doit se voir dans le modèle ! Il faut donc avoir une approche différente pour construire le modèle complet d’un bras de robot, et ce sont les équations de Lagrange qui vont nous fournir la solution.

Pour les mettre en œuvre, on commence par rassembler les données géométriques et mécaniques dont on dispose sur le bras du robot : dimensions, masses, inerties, etc. On peut alors établir l’expression de l’énergie cinétique, qui dépend de la configuration et des vitesses articulaires. Avec les mêmes données, on calcule l’énergie potentielle, représentant l’action de la pesanteur. Celle-ci est également fonction de la configuration.

Ensuite, on applique les formules de Lagrange et, hop, on obtient la version « propre » de l’équation déjà citée. On a donc finalement la belle équation ci-dessous (tout ceci peut se faire à la main, très laborieusement, mais, ouf, de nombreux et performants logiciels de calcul formel permettent aussi de sous-traiter ce travail à notre ordinateur favori) :
\[ \Gamma = M (\mathbf{q}) \ddot{\mathbf{q}} + N(\mathbf{q}, \dot{\mathbf{q}}) \dot{\mathbf{q}} + G(\mathbf{q}) + F(\mathbf{q},\dot{\mathbf{q}}) \:\: \mbox{ équation }(1).\]

Pour comprendre en détail la signification de cette équation, quelques précisions ne sont pas de trop :

• \(\Gamma\) est un vecteur représentant les \(n\) forces ou couples extérieurs appliqués aux \(n\) articulations. Ceci veut dire qu’il ne s’agit pas de ce qui sort du moteur, mais de ce qui arrive après transmission (de la même façon que ce qui compte pour faire avancer un vélo, ce n’est pas tant l’effort appliqué sur les pédales en lui-même que le couple effectivement exercé sur le moyeu arrière en bout du système pédalier-chaîne-changement de vitesse).
• \(M(\mathbf{q})\) est la matrice \(n \times n\) qui intervient dans l’expression de l’énergie cinétique \(K\), appelée pour cette raison matrice d’énergie cinétique. Elle est, pour un système articulé, analogue de la masse pour un objet ponctuel ou de l’inertie pour un corps rigide. Elle dépend de la configuration – observez un patineur : pourquoi sa vitesse de rotation augmente-t-elle lorsqu’il plaque ses bras le long du corps ? C’est parce que son inertie, qui dépend de sa posture, a diminué, et que le produit de la vitesse de rotation par l’inertie reste constant. Le théorème classique de la mécanique qui s’applique ici s’appelle la conservation du moment cinétique.
• \(\ddot{\mathbf{q}}\) est le vecteur des accélérations articulaires, regroupant les dérivées secondes des coordonnées articulaires.
• \(N(\mathbf{q}, \dot{\mathbf{q}}) \dot{\mathbf{q}}\) provient du caractère non linéaire et couplé du système (les mouvements influent les uns sur les autres). Certains coefficients sont en \(\dot{q_i}^2\) : ils représentent la force centrifuge,vous savez, celle qui peut nous faire déraper dans les virages. D’autres termes sont en \(\dot{q_i} \dot{q_j}\). Ceux-là modélisent la force de Coriolis, celle qui donne le sens de rotation des dépressions atmosphériques selon l’hémisphère.
• \(G(\mathbf{q})\) : ce terme-là, c’est l’effet du poids des éléments du robot sur chaque articulation. Comme l’énergie potentielle dont il dérive, il dépend de la configuration : si vous tendez le bras avec une enclume dans la main, l’effort sur l’épaule sera plus élevé que si vous le repliez complètement ! Et si le robot est dans un liquide de densité ad-hoc ou en apesanteur, alors \(G(\mathbf{q})\) est nul !
• \(F(\mathbf{q},\dot{\mathbf{q}})\) : ce terme représente les forces engendrées par les frottements, qui ne font rien que ralentir les mouvements et dissiper de l’énergie en chaleur. Il y en a de deux sortes : les frottements secs, qui impliquent qu’un couple minimal est nécessaire au déclenchement d’un mouvement (comme pour déplacer une armoire sur un plancher), et les frottements visqueux (beuh…), croissant avec la vitesse. D’ailleurs ceux-ci sont de même nature que le terme en \(k_v \dot{theta}\) que nous avons utilisé pour freiner le pendule. Dans les deux cas, la dissipation d’énergie induite va avoir pour conséquence un ralentissement des mouvements.

La commande

Comme on l’a constaté, le bras de robot est légèrement plus compliqué que le pendule du Professeur Tournesol. Le roboticien, qui n’est qu’un paresseux, va donc chercher à se ramener le plus près possible de la situation la plus simple. Comment ? En travaillant en deux étapes :

1. Nous l’avons vu, l’équation (1) comporte plein de termes compliqués dont l’effet sur la commande peut être pernicieux. Une première opération consiste donc tout bêtement à s’en débarrasser, et ceci en écrivant la commande sous la forme :
   \[ \Gamma = M (\mathbf{q}) u + N(\mathbf{q}, \dot{\mathbf{q}}) \dot{\mathbf{q}} + G(\mathbf{q}) + F(\mathbf{q},\dot{\mathbf{q}}) \:\: \mbox{ équation }(2).\]
   On utilise ainsi explicitement le modèle dynamique calculé dans l’expression de la commande qui sera envoyée aux moteurs. Pour briller dans les salons, sachez que cette opération est qualifiée de découplage et linéarisation par feedback. À noter que les mécaniciens peuvent aussi mettre leur grain de sel dans l’affaire en compensant plus ou moins complètement la pesanteur au niveau du robot lui-même, par d’astucieux dispositifs à base de ressorts ou de contrepoids.
2. La commande formulée dans l’équation (2) appliquée à l’équation (1) nous donne le résultat le plus simple possible :

\[ \ddot{\mathbf{q}} =u \:\: \mbox{ équation }(3).\]
soit un ensemble de \(n\) équations différentielles linéaires indépendantes \(\ddot{q_i} = u_i\).

Pour que notre bras se positionne à la posture spécifiée par les angles articulaires \(q^d_i\) et y reste, grâce à l’asservissement, il suffit d’appliquer à ces équations une commande proportionnelle dérivée, version simple d’une commande par retour d’état (feedback), analogue à celle du pendule :
\[ u_i = k_p^i (q_i-q_i^d) =k_v^i q_i, \:\: i=1 \ldots n \:\: \mbox{ équation } (4).\]

Fort bien, mais il est rare qu’un bras de robot soit juste destiné à rester immobile dans une configuration donnée. Heureusement, la méthode précédente se généralise aisément au cas où l’on désire suivre une trajectoire articulaire dépendant du temps, \(\mathbf{q}^d(t)\), plutôt qu’atteindre un point ou un ensemble de points successifs.

3. Mais que va-t-on faire de ce robot ?

Nous disposons donc à ce stade, chanceux que nous sommes, d’un bras de robot muni d’une commande permettant de lui faire suivre n’importe quelle trajectoire articulaire, ou presque. Entre alors en scène notre ami Grincheux : « Ton robot, il ne sert à rien, là. Ma pomme est tombée par terre et comme je suis perclus de rhumatismes, je ne peux pas la ramasser. Ton robot me serait bien utile, mais tu ne peux pas lui dire comment faire, puisque tu ne sais pas lui fixer autre chose que des consignes articulaires. Tu parles d’un intérêt ! ». Dans un sens, Grincheux n’a pas tort… mais nous avons des réponses à lui apporter.

De l’espace articulaire à l’espace environnant (et inversement)

Supposons pour l’instant que nous sachions exactement où se trouve la pomme par rapport au robot et que celui-ci dispose d’un préhenseur adapté à la saisie des pommes. La tâche à effectuer consiste à amener celui-ci à une position, et dans une orientation, permettant cette saisie. On retrouve ici notre vieille connaissance, ℜ³ × SO(3), qui est aussi l’espace de configuration de la pomme. Du coup, la « consigne » à atteindre dans cet espace est un ensemble de 6 coordonnées (3 longueurs, 3 angles), que l’on peut noter \(\mathbf{x}^d = (x^d,y^d,z^d,\theta^d,\phi^d,\psi^d)\).

Il ne reste plus qu’à calculer la relation générique liant \(\mathbf{x}\) à \(\mathbf{q}\), \(\mathbf{x} = f(\mathbf{q})\) puis à l’inverser pour trouver le vecteur \(\mathbf{q}^d\) représentant la trajectoire articulaire désirée.

Deux règles constituent un « robot » plan à deux articulations.

Sauf que ce n’est pas si simple. Pour nous en convaincre, récupérons les règles qui nous ont servi à réaliser le parallélogramme de la petite vidéo de la page 1, et assemblons en deux de même longueur \(l\) pour constituer un « robot » plan à deux articulations. La première règle fait un angle \(q_1\) avec l’horizontale, la deuxième un angle \(q_2\) avec la première. Les coordonnées du point terminal sont :
\(x=l ( \cos(q_1) + \cos(q_1+q_2))\) ; \(y=l(\sin(q_1)+\sin(q_1+q_2))\)

Lorsqu’on est familier de ce genre d’équations, il n’est pas bien difficile d’inverser cette relation analytiquement. Le lecteur sceptique, pour peu qu’il soit un peu matheux, pourra effectuer le calcul à titre d’exercice.

Mais l’on voit déjà apparaître sur cet exemple simple les difficultés inhérentes à l’inversion de \(f\) : tout d’abord, il faut qu’il existe une solution. En effet, si le point visé est en dehors du cercle de rayon \(2l\), aucune valeur des angles ne permettra de l’atteindre. Donc, alors que toutes les valeurs angulaires sont permises, les valeurs atteignables dans l’espace environnant sont limitées. Leur ensemble est d’ailleurs appelé espace atteignable, et sa caractérisation pour un robot complexe n’est pas toujours évidente à calculer ni à visualiser.

Ensuite, il peut exister plusieurs solutions au problème – ce que l’on pressent dans l’exemple, si l’on se souvient que deux angles opposés ont le même cosinus.

Et enfin, il apparaît la délicate question des singularités. En gros, il s’agit d’un ensemble de positions du robot dans lesquelles l’inversion de la fonction \(f\) se passe très mal…

Dans notre exemple, les points singuliers sont :

• l’origine (\(x=y=0\)). En effet, lorsque l’extrémité du bras se trouve en ce point, l’angle \(q_1\) est quelconque (le robot tourne autour de l’origine) ;
• le cercle de rayon \(2l\). Ici, le bras est totalement étendu. Il est en limite de mouvements (on ne peut plus avoir de vitesse allant vers l’extérieur du cercle) et, si on veut le replier, il existe une indétermination : veut-on le « coude » en haut ou en bas ?

Allons un peu plus loin

Les robots opérationnels dans l’industrie, comme les robots expérimentaux des centres de recherche, sont conçus à partir de ces principes de base. Mais selon les tâches qu’ils ont à effectuer, ils peuvent présenter d’autres fonctionnalités, qui nécessitent d’adapter les techniques de commande.

Bras robotique en contexte industriel.
Vidéo © INRIA – Durée : 13 s.

De nombreuses dimensions

Le squelette humain adulte comporte un peu plus de 200 os. Selon les définitions utilisées, il possède de 100 à 200 articulations, dont 8 pour le bras, sans tenir compte de celles de la main. Autant dire que notre robot à 6 axes fait piètre figure. Alors, pourquoi ne pas imaginer des robots présentant un nombre supérieur d’articulations, même s’il s’agit juste de positionner et d’orienter dans l’espace un dispositif terminal ? De tels robots existent, et sont communément appelés redondants. Leur intérêt est d’offrir, pour un ensemble de coordonnées à atteindre \(\mathbf{x}^d\) donné, un ensemble continu de solutions articulaires possibles \(\mathbf{q}\). Ceci permet par exemple d’assurer le positionnement requis en évitant un obstacle, ou en se situant dans une configuration sympathique pour le robot (loin des limites articulaires mécaniques par exemple). La fonction \(f\) n’est alors plus inversible. Des méthodes de résolution existent cependant, qui tirent parti de ces degrés de liberté supplémentaires pour choisir la « meilleure » solution au sens d’un critère défini par l’utilisateur.

Mais le lecteur avisé (encore lui) nous fait finement remarquer : « Mais dites-moi, M’sieur, pourquoi s’embêter avec des dimensions différentes ? Ne pourrait-on pas une bonne fois pour toutes en avoir autant en entrée qu’en sortie, quitte à définir des tâches plus générales que la position et l’orientation d’une pince de robot ? ». Bien vu ! De fait, le problème du ramassage de la pomme se généralise à toute tâche possible (ou à peu près) en définissant celle-ci sous la forme d’une fonction d’erreur à annuler, que l’on notera \(e\) pour la distinguer de \(e\). Et puis, pour prendre en compte des trajectoires dans ce nouvel espace de sortie, on la rendra dépendante du temps, comme l’était \(\mathbf{q}^d(t)\), souvenez-vous. Le lecteur avisé (toujours le même, quel fayot celui-là) fait alors finement remarquer : « Et la commande, M’sieur, vous savez, celle que l’on a vue avant, il faudrait peut-être la modifier, non ? ». Bon. Bien qu’il ait raison, là ça devient un petit peu plus difficile. Mais, le roboticien étant toujours aussi paresseux, l’idée reste la même : se débarrasser de tous les termes compliqués. À la dynamique intrinsèque du bras s’ajoutent ici les termes non-linéaires issus du changement d’espace. Pour avoir une idée de la démarche à suivre dans un espace de tâche général, dépliez le paragraphe suivant.

Mais regarde donc ce que tu fais !

Jusqu’ici, notre bras de robot n’était doté que des sens lui permettant de faire fonctionner sa commande articulaire : des capteurs de vitesse et de position, proprioceptifs, étaient en effet suffisants pour cela. Mais à présent, il faut aussi le munir des sens nécessaires à l’accomplissement d’une tâche dans l’espace environnant. Ceux-ci sont essentiellement la vue et le toucher, réalisés technologiquement par des capteurs de vision, d’effort, et tactiles, qui sont extéroceptifs.

Positionnement de l’organe terminal d’un bras robotique (ici avec asservissement visuel).
Vidéo © INRIA – Durée : 1 min 41 s.

Chez l’homme, il existe deux niveaux principaux de boucles associant perception et action : les actions réfléchies, qui impliquent un travail complexe du cerveau, et les actions réflexes, localisées au niveau de la moelle épinière. Pour un robot, l’analogie avec les premières se situe dans les fonctions de compréhension de l’environnement, modélisation, planification, décision. Par exemple, la détermination des valeurs de consigne en position et en orientation de l’organe terminal à partir d’images numériques d’une scène est de cette nature. Pour rester dans le domaine de la commande, nous nous intéresserons ici à la seconde catégorie.

Dans ce cadre, un capteur extéroceptif est vu comme un dispositif permettant de donner en continu une information quantitative simple sur la tâche en cours. Par exemple, une caméra embarquée dans un organe terminal de robot (« l’œil dans la main ») ne sera dans ce contexte utilisée que pour fournir une mesure de l’écart entre la main et l’objet à saisir. L’introduction de cette mesure dans la commande constitue ce que l’on appelle un « asservissement visuel ».

Pour illustrer notre propos, prenons deux autres exemples.

Maîtriser sa force

Récupérons notre règle favorite et observons ce qui se passe d’un point de vue mécanique lorsque nous tirons un trait avec un crayon, la règle étant maintenue fixe par l’autre main. Le mouvement du crayon est « libre », c’est-à-dire avec des vitesses décidées par le tireur de trait, selon 4 directions dans notre espace désormais familier ℜ³ × SO(3) : 1 dimension en translation le long du trait, et les 3 dimensions de rotation du crayon (en pratique dans un certain domaine de confort de traçage). Le lecteur avisé (tiens, ça faisait longtemps qu’il ne s’était pas manifesté, celui-là) remarque de suite que les deux autres dimensions sont contrôlées en force et non pas en mouvement : on s’appuie le long de la règle (orthogonalement au déplacement), avec une force suffisante pour que le trait soit droit, mais sans faire bouger la règle, et on contrôle la force d’appui vers le bas pour que le trait soit net et que l’on ne déchire pas le papier.

Pour un robot, le problème est posé de façon analogue. De nombreux robots industriels ont en effet vocation à effectuer des tâches nécessitant un contrôle simultané des mouvements et des efforts exercés : polir une pièce, réaliser un assemblage, graver, visser un boulon, assister une intervention chirurgicale, etc. La commande associée, appelée en général « commande hybride », requiert l’accès à une mesure permanente des efforts exercés. Celle-ci est réalisée par des capteurs que l’on essaye en général de placer le plus près possible de la tâche : capteurs génériques de « poignet », ou capteurs plus spécifiques dans les doigts ou les outils. Le principe de ceux-ci est simple : un corps mécanique ad-hoc se déforme sous l’effet des forces exercées. Le microdéplacement associé est mesuré par un dispositif adapté : jauge de contrainte, microcapteur optique, capteur piézo-électrique. La comparaison entre ces efforts mesurés et ceux désirés permet de construire une partie du signal d’erreur \(e\) utilisé dans la commande. Les aspects théoriques sous-jacents concernent efforts et vitesses, la relation force-vitesse constituant l’un des grands classiques de la mécanique des solides.

Le toucher à distance

Voilà un titre bien mystérieux. Il n’y a pourtant là rien de magique… En effet, le roboticien qui, il faut le rappeler, n’est qu’un paresseux, a pour penchant naturel de ne pas multiplier les algorithmes de commande différents. Son idée est donc de réutiliser, autant que faire se peut, les méthodes exposées précédemment, tant pour la commande dans un espace de tâche général que pour celle en efforts. Voyons cela d’un peu plus près.

C’est l’heure de la sieste du Professeur Tournesol ; nous pouvons donc lui chiper discrètement son pendule. Comme tout à l’heure, on le bloque pour qu’il lui reste juste un mouvement possible dans le plan, on lui colle un moteur dans l’axe et une commande proportionnelle dérivée. Effectuons maintenant deux expériences avec ce système :

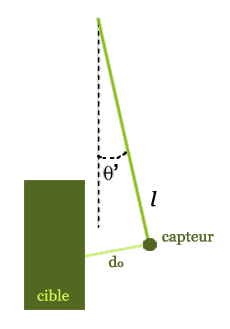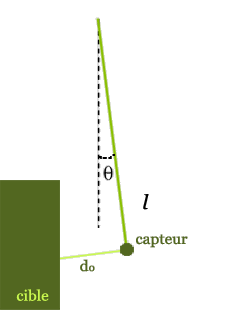
Expérience de toucher à distance.
Quand on déplace la cible, le pendule asservi à la consigne \(d_0\) se déplace également.

• Expérience 1 : Réglons la consigne de l’asservissement à 30 degrés, par exemple. Pouf, le pendule se positionne alors en présentant un angle de 30 degrés avec la verticale. Poussons-le à présent doucement avec le doigt pour tenter de l’écarter de cette position. On va alors ressentir une force de résistance de plus en plus élevée au fur et à mesure que l’on va l’écarter, comme avec un ressort. C’est en fait la partie de la boucle \(k_p (\theta_d – \theta)\) réalisant cette régulation de la position qui synthétise l’effort ressenti, alors qu’il n’y a aucun ressort réel dans le système. Et l’on peut renouveler l’expérience sur tout système motorisé asservi en position ! On en retiendra que l’on peut simuler une force analogue à celle produite lors d’un contact avec un objet immobile, grâce à une boucle de régulation.
• Expérience 2 : Fixons à présent à l’extrémité du pendule un petit dispositif permettant de mesurer une distance : capteur laser (comme ceux utilisés pour la mesure des dimensions entre murs dans un logement), télémètre à ultrasons ou optique (pensez à la mise au point automatique de votre appareil photo)… Si l’on débranche le capteur de position angulaire utilisé précédemment et que l’on remplace celui-ci dans la commande par la sortie du télémètre, alors le système va s’asservir à une consigne \(d_0\). Et en renouvelant l’expérience 1, on ressent alors un effort en s’approchant ou en s’éloignant de la cible… comme si on la touchait de loin ! De plus, si l’on déplace la cible, l’extrémité du pendule va suivre ce déplacement.

De plus, dans l’expérience 2, si on place la cible à la verticale du pendule, la distance du capteur à la cible est \(d=l \tan \theta\). Ainsi, \(d\) et \(\theta\) varient dans le même sens, et sont même presque proportionnels si l’angle est petit. Il est donc facile de changer de variable contrôlée. Et ceci se généralise à tout type de commande avec capteurs sans contact.

C’est l’heure de la sortie

Notre promenade-découverte de la commande des bras de robots s’achève. Nous y avons croisé le Professeur Tournesol, Grincheux, un lecteur avisé un peu collant, un roboticien paresseux, erré dans des espaces bizarres et découvert les vertus de la commande proportionnelle dérivée. Nous avons constaté que nous pouvions dissocier la notion de bras de celle de tâche à effectuer en définissant des espaces de sortie adéquats, particulièrement ceux dans lesquels le robot possède des entrées sensorielles. Et nous avons même inventé le toucher à distance. Il resterait pourtant bien des sujets à évoquer avant d’imaginer avoir fait le tour de la commande des robots.

Parmi ceux-ci, l’un des plus intéressants est celui de la coordination. Comment manipuler un Rubik’s Cube ou transporter délicatement une pile d’assiettes en utilisant deux bras (ou plus, pourquoi pas ?)… Comment coordonner le mouvement d’un bras avec un déplacement, pour asséner un revers définitif pendant la coupe Davis des robots ? Un robot peut-il grimper à une échelle ? L’homme et le robot peuvent-ils se donner la main, travailler ensemble ? Toutes ces questions peuvent aujourd’hui recevoir des réponses, souvent partielles, à l’aide de techniques de commande, disons sophistiquées pour être pudique. Et l’un des grands défis de l’avenir est de rendre plus faciles la conception et la mise en œuvre robuste d’applications de commande complexes pour les robots.

Cela peut passer par des prouesses mathématiques, mais aussi par d’autres voies. Parmi celles-ci, les techniques d’apprentissage, envisageant le développement des robots de façon analogue à celui des enfants, sont particulièrement prometteuses. Elles permettent d’appréhender progressivement la complexité du monde sans nécessairement en tenter une modélisation exhaustive, d’ailleurs vite impossible. À quand le recyclage des automaticiens dans les nurseries de robots ?