
Tout a un reflet numérique
À chaque instant, notre cerveau capte, enregistre, et traite des informations. Ainsi pouvons-nous regarder, mémoriser, analyser, puis retranscrire une image, un texte ou un son. Depuis longtemps, l’homme a cherché à capter et reproduire ce reflet de la réalité par un dispositif technique. Et il a inventé le téléphone, la photographie, le cinéma… Mais qu’en est-il aujourd’hui, avec les machines que nous utilisons, qui sont des dispositifs de calcul programmé ?
L’information et son reflet
Prenons l’exemple d’une calculette électronique : quand nous disons qu’elle « calcule », ses circuits électriques s’ouvrent et se ferment de manière à ce que l’affichage corresponde au résultat du calcul effectué. Mais le fait que cela prenne le sens d’un calcul est le fait de l’humain qui utilise cette calculette ; la machine ne « comprend » évidemment pas les calculs qui s’exécutent uniquement grâce aux propriétés électriques de ses circuits : la calculette ne possède que le reflet électronique du calcul.
Information, hasard et complexité
Regardons cette suite de chiffres :
14159 26535 89793 23846 26433 83279 50288 41971
Il y a sûrement plus d’informations dans cette suite là que dans celle-ci :
00000 00000 00000 00000 00000 00000 00000 00000
qui n’est qu’une suite de zéros. Ah oui, mais en quoi la première suite de chiffres est-elle plus complexe ?
- Est-elle aléatoire, chaotique, bref sans ordre ni régularité ?
- Ou bien organisée, fortement structurée, riche en information « utile » ?
En fait, si nous regardons bien le début de cette suite, nous reconnaissons les premières décimales de π, peut-être le nombre le plus célèbre de toute l’histoire des mathématiques : autant dire que son information est très utile… du moins pour les géomètres et les mathématiciens !
En tout cas, il est bien compliqué de retenir les chiffres de la première suite (et sans doute même impossible de faire autrement que de les apprendre par cœur). Mais pour la deuxième suite, il suffit de retenir : « voilà 8 fois 5 zéros ».
Cet exemple, dû à Jean-Paul Delahaye dans son ouvrage Information, complexité et hasard, est très instructif car il nous montre que nous devons bien distinguer :
- le contenu brut en information, qui ne dépend pas du sens ;
- et la valeur d’une information, qui elle dépend du but fixé.
Voir aussi sur Interstices : Théories et théorie de l’information.
Fabriquer un reflet numérique d’un objet réel
Afin de mieux percevoir l’importance du concept d’information, commençons par la première étape : la façon dont on introduit l’information dans une machine, dont on la code pour pouvoir ensuite la manipuler. Dans le but de comprendre ses retombées concrètes dans les systèmes et logiciels qui nous entourent, nous avons choisi d’illustrer les principes de codage dans le contexte des images numériques. Le document Nom de code : binaire offre une introduction au sujet traité ici.
Regardons tout d’abord en détail un exemple : comment coder un dessin au tracé simple. Nous découvrirons ensuite que la méthode peut être aussi appliquée à une photo, un texte, un son, des nombres, et que finalement… on peut convenir d’un codage pour toutes les informations !
Nous distinguerons comment coder l’information selon qu’elle est discrète, c’est-à-dire qu’on peut la dénombrer (par exemple, les lettres d’un alphabet), ou continue, auquel cas on doit sélectionner un nombre fini d’échantillons qui la représentent et à partir desquels il est possible de reconstruire une approximation du signal original (par exemple, un son).
Les codages que nous allons décrire ici sont des codages binaires, nous expliquerons pourquoi. Puis nous reviendrons à la notion d’information et verrons en particulier comment elle se mesure, presque comme toute autre quantité.
Décrire un dessin par une définition structurée
Comment faire pour décrire un dessin ? Par exemple, comment décrire le dessin suivant ?
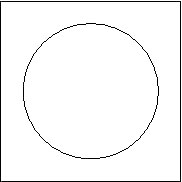
Une solution est de dire : « Cette image est formée d’un cercle ». Nous pouvons même être plus précis et indiquer les coordonnées du centre du cercle, son rayon, sa couleur, l’épaisseur du trait… À partir de cette description, n’importe qui pourrait reconstituer le dessin.
Explorons rapidement une autre voie pour décrire, par exemple, le dessin suivant :

Une solution est donc de dire : « Cette image est formée d’un cercle ».
Pour permettre de reproduire l’image, nous devons être plus précis et indiquer les coordonnées du centre du cercle, son rayon, sa couleur… Comment formaliser, structurer de manière rigoureuse tous ces éléments ? Nous ne pouvons pas nous exprimer avec des phrases : la machine ne comprendrait rien ! Nous pouvons, en revanche, oublier la belle syntaxe de notre langue humaine et écrire quelque chose comme :
|
<cercle
abscisse=« 100 »
ordonnée=« 100 »
rayon=« 200 »
couleur=« noir »
/>
|
|---|
qui se traduirait par : « Voilà un cercle qui a pour centre le point d’abscisse (ou position horizontale) 100 et d’ordonnée (ou position verticale) 100, de rayon 200 et de couleur noire ».
Cette façon de spécifier notre information sous forme structurée est universelle. Nous pourrions, par exemple, spécifier un dessin plus compliqué, comme celui-ci :
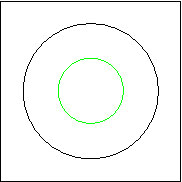
Pour cela, nous pourrions écrire :
|
<dessin>
<cercle
abscisse=« 100 »
ordonnée=« 100 »
rayon=« 200 »
couleur=« noir »
/>
<cercle
abscisse=« 100 »
ordonnée=« 100 »
rayon=« 100 »
couleur=« vert »
/>
</dessin>
|
|---|
Ce qui se traduirait par : « Voilà un dessin constitué de deux cercles [ etc.] de couleur noire et [ etc.] de couleur verte ».
Nous avons en quelque sorte « démonté la grammaire de la phrase » pour n’en garder que la structure logique et les données qui y sont contenues. En d’autres termes, nous avons séparé le fond de la forme, pour permettre à l’ordinateur de manipuler cette information symbolique.
Cette façon de présenter l’information de manière symbolique utilise une syntaxe que l’on appelle « structure logique XML ». Elle utilise deux constructions très simples :
- Des ensemble d’attributs, par exemple les paramètres de notre cercle.
- Des listes d’éléments, par exemple notre dessin constitué d’une liste de deux éléments, les deux cercles qui le composent.
De même, un texte n’est pas seulement une suite de mots, il a une structure (des paragraphes, des sections, des références…), il a des méta-données (son titre, son auteur, la langue dans laquelle il a été écrit…) et tous ces éléments peuvent être spécifiés grâce aux constructions que nous évoquons ici.
Sous le nom de HTML, que vous connaissez sans doute déjà, toutes les pages du Web sont codées de manière similaire. La syntaxe (c’est-à-dire la façon de coder cette information symbolique) varie un peu, mais les fondements sont les mêmes.
Sans oublier qu’au bout du compte, pour être manipulé par l’ordinateur, tout ceci est codé… en binaire.
Cette méthode marche bien pour ce dessin-ci. Mais tout décrire avec des mots serait bien moins pratique pour le dessin suivant :

En effet, comment facilement décrire en détail ces traits qui semblent tracés au hasard ? Qu’en serait-il avec un dessin qui représente un objet réel, ou un visage ?
Décrire avec des nombres binaires
Une autre méthode, qui a l’avantage de pouvoir être utilisée pour n’importe quel dessin, consiste à superposer un quadrillage au tracé :
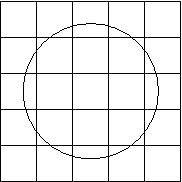
Chacune des cases de ce quadrillage s’appelle un pixel (contraction de picture element, en anglais). On noircit ensuite les pixels qui contiennent une portion de trait :

Puis, il nous suffit d’indiquer la couleur de chacun des pixels, en les lisant de gauche à droite et de haut en bas, comme un texte (dans notre culture occidentale).
Ici, cela donne : blanc, noir, noir, noir, blanc, noir, noir, blanc, noir, noir, noir, blanc, blanc, blanc, noir, noir, noir , blanc, noir, noir, blanc, noir, noir, noir, blanc.
De fait, cette description est assez approximative, et on constate une grande différence entre ces deux images :
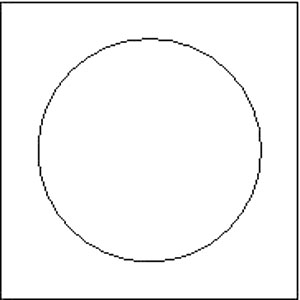

Mais nous pouvons rendre la description plus précise en utilisant un quadrillage, non plus de cinq x cinq, mais de cent x cent pixels :

Et à partir de quelques millions de pixels, nous ne serions plus capables de faire la différence entre les deux images.
Cette méthode est donc approximative, mais universelle : n’importe quel dessin, même très compliqué, se décrit exactement comme un dessin simple.
Ce dessin se décrit donc par une suite de mots « blanc » ou « noir ». Comme seuls les mots « noir » ou « blanc » sont utilisés, nous pouvons être plus économes et remplacer chacun de ces mots par un seul symbole, par exemple le mot « noir » par la lettre « n » ou le chiffre « 0 » et le mot « blanc » par la lettre « b » ou le chiffre « 1 ».
Le dessin ci-dessus, avec une grille de 5 x 5, se décrit alors par la suite de 25 chiffres :
1000100100011100010010001
Ces différentes descriptions sont équivalentes : le dessin se décrit toujours par une suite de symboles choisis parmi deux. Le nom de ces deux symboles importe peu, et nous pourrions les appeler noir et blanc, a et b, 0 et 1, pile et face, – et +, Dupond et Dupont… que cela ne changerait pas grand-chose. En général, on choisit 0 et 1. Ces symboles s’appellent les chiffres binaires ou bits (abréviation de binary digits, « chiffres binaires », en anglais).
Une suite de 0 et de 1 s’appelle une suite binaire, ou parfois un mot binaire. Notre dessin se décrit ainsi avec 25 chiffres binaires, ou encore 25 bits ; sa longueur est 25.
Le point clé : convenir d’un standard pour toutes et tous
Bien entendu, il faut que nous soyons tous d’accord pour décrire tous les dessins de la même façon !
Décider, comme nous l’avons fait dans l’exemple précédent, que le noir est représenté par 0 et le blanc par 1 et que les pixels se lisent de gauche à droite et de haut en bas.
Il faut se mettre d’accord sur un standard. Le codage de l’information est avant tout une affaire de… convention. Regardons alors comment nous pourrions convenir de représenter d’autres objets.
Décrire numériquement toutes sortes d’objets
Du dessin aux images photographiques
Si nous voulons maintenant décrire une image en couleur, par exemple une image dans laquelle chaque pixel peut être noir, rouge, vert ou bleu, une première méthode consiste à la décrire par une suite dont chaque élément est l’un des quatre mots « noir », « rouge », « vert », « bleu ». Par exemple, prenons l’image suivante :

Elle se décrit par la suite : noir, rouge, noir, rouge, noir, noir, rouge, noir, rouge, noir, bleu, noir, bleu, noir, vert, bleu, bleu, noir, bleu, vert, bleu, bleu, vert, vert, vert.
Comme pour les images en noir et blanc, on peut être plus économe et décrire chaque couleur par une seule lettre ou un seul chiffre. Par exemple, en utilisant la correspondance :
| n | noir |
| r | rouge |
| v | vert |
| b | bleu |
cette image se décrit par la suite
nrnrnnrnrnbnbnvbbnbvbbvvv
Cela fonctionne à condition, bien entendu, que celui qui code et celui qui décode cette image suivent parfaitement le standard proposé ici.
Cette méthode utilise quatre symboles différents. Il est possible aussi de décrire cette image par une suite binaire, c’est-à-dire dans laquelle on utilise seulement deux symboles différents et non quatre. Mais comme il y a plus de deux couleurs, il est impossible de décrire chaque couleur par un seul chiffre binaire : un « 0 » ou « 1 ».
En revanche, on peut décrire chaque couleur par une suite de deux bits. Par exemple :
| '00' | noir |
| '01' | rouge |
| '10' | vert |
| '11' | bleu |
L’image ci-dessus se décrit alors par la suite
donc 25 x 2 = 50 bits. Les espaces entre chaque couple de valeurs binaires sont inutiles, sauf pour… en faciliter la lecture !
Une fois choisis le nombre de pixels de l’image (ici 5 x 5, pour une photo numérique il en faudrait quelques millions) et le nombre de bits sur lequel on représente la couleur de chaque pixel (ici 2 bits, en réalité de 8 à 32 bits, selon la palette des couleurs), toutes les images se représentent par une suite binaire de la même longueur : cette longueur s’obtient simplement en multipliant le nombre de pixels de l’image par le nombre de bits utilisés pour décrire la couleur d’un pixel. C’est ainsi que se décrivent les photographies dans les ordinateurs et les autres machines numériques.
Décrire des textes par des suites binaires
Décrire un texte semble a priori plus simple que décrire une image, puisqu’un texte est déjà une suite de symboles : c’est déjà une suite de lettres de l’alphabet. L’alphabet latin, que l’on utilise en français, contient 26 lettres. Mais en fait, quand on compte les majuscules et les minuscules, les lettres accentuées, les chiffres et les symboles de ponctuation, écrire en français nécessite plutôt une centaine de symboles.
Et puis, il faut aussi pouvoir décrire toutes les autres langues du monde. Par exemple, les 28 symboles de l’alphabet arabe, avec ses symboles complémentaires, comme on les devine sur cette ancienne machine à écrire :

Ainsi la phrase : « tout se code en binaire » s’écrira «كل شيء في ثنائي الكود» (qui se lit de droite à gauche) et se codera, par exemple :
1011 1100 1001 1111 0000 1010 1111 0111 1101 0110 0101 1111 0110 1100 1011 1110 1000
en utilisant les codes binaires à 4 bits des 16 lettres suivantes :
| ء | آ | أ | ؤ | إ | ئ | ا | ث | د | ش | ف | ك | ل | ن | و | ي |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Ce code de seize lettres, nous nous sommes amusés à l’inventer juste pour cette présentation. Cependant, là encore, pour partager les informations, il ne faut pas utiliser un code particulier comme celui-ci, mais un code standard, adopté par tous et qui représente tous les caractères de la langue utilisée.
Les caractères les plus courants en Occident, ceux que nous tapons au clavier, sont codés sur 8 bits, avec un code universel, dit ASCII (pour American Standard Code for Information Interchange) étendu.
Pour coder tous les textes du monde, c’est l’Unicode, contenant plus de 120 000 caractères, qui est utilisé. Ce standard utilise le code ASCII et des codes complémentaires à 16 ou 24 bits.
Décrire des nombres
Le codage des valeurs numériques est de nature différente, car ce n’est pas un code arbitraire « standard », mais un choix issu de l’arithmétique.
En effet, il serait possible de représenter un nombre tel que 2741 comme la succession des caractères ‘2’, ‘7’, ‘4’ et ‘1’, puis de coder chacun de ces caractères par son équivalent ASCII pour obtenir ainsi : 00110001 00110111 00110100 00110001. Mais, si un tel codage représente bien la chaîne de caractères ‘2741’, il ne représente pas le nombre 2741 et ne permet pas d’effectuer dessus des calculs arithmétiques tels que l’addition ou la multiplication. Pour obtenir une représentation utilisable dans des calculs, il suffit cependant de passer de la numération à base 10 classique à la numération à base 2. Découvrons ensemble le principe de ce changement de base.
Le tableau suivant donne les 10 premiers nombres en base 10 dans la colonne du milieu et leur représentation binaire dans la colonne de droite :
| 0 x 8 + 0 x 4 + 0 x 2 + 0 x 1 = | 0 | 0000 |
| 0 x 8 + 0 x 4 + 0 x 2 + 1 x 1 = | 1 | 0001 |
| 0 x 8 + 0 x 4 + 1 x 2 + 0 x 1 = | 2 | 0010 |
| 0 x 8 + 0 x 4 + 1 x 2 + 1 x 1 = | 3 | 0011 |
| 0 x 8 + 1 x 4 + 0 x 2 + 0 x 1 = | 4 | 0100 |
| 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = | 5 | 0101 |
| 0 x 8 + 1 x 4 + 1 x 2 + 0x 1 = | 6 | 0110 |
| 0 x 8 + 1 x 4 + 1 x 2 + 1 x 1 = | 7 | 0111 |
| 1 x 8 + 0 x 4 + 0 x 2 + 0 x 1 = | 8 | 1000 |
| 1 x 8 + 0 x 4 + 0 x 2 + 1 x 1 = | 9 | 1001 |
Si vous observez bien ce codage, vous constaterez quelque chose de plus : il est le résultat d’un calcul, montré dans la colonne de gauche. Le codage binaire d’un nombre (que nous, humains, écrivons quasiment toujours en base 10, en utilisant 10 chiffres), est ce même nombre, écrit en base 2.
Du codage binaire au nombre entier positif
Voici le calcul qui permet de retrouver un nombre à partir de son code binaire : additionner les bits, chacun multiplié par la puissance de deux qui lui correspond, comme ci-dessous, donne le nombre en base 10.
| 1 x 8 + 0 x 4 + 0 x 2 + 1 x 1 | = | |
| 1 x 23 + 0 x 22 + 0 x 21+ 1 x 20 | = | 9 |
| ((1 x 2 + 0) x 2 + 0) x 2 + 1 | = |
- À la première ligne, nous avons multiplié respectivement par 1, 2, 4, 8 de droite à gauche les bits qui représentent 9.
- À la seconde ligne, nous nous sommes aperçus que 1, 2, 4, 8 sont en fait les puissances de 2 : 20, 21, 22…
- À la troisième ligne, nous factorisons 2 autant que possible ; cette écriture avec ses parenthèses bien placées nous montre qu’il suffit de multiplier par deux puis d’additionner les bits de gauche à droite pour trouver le nombre en base 10.
Voilà donc un calcul, une méthode mécanique que l’on appelle algorithme, qui permet de passer du codage binaire au nombre dans sa représentation usuelle.
Du nombre entier positif à son codage binaire
Réciproquement, il existe un calcul pour obtenir le code binaire de n’importe quel nombre entier. Si nous notons 9 % 2 = 1 le reste de la division par 2 de 9 ou 4 % 2 = 0 le reste de la division de 4 par 2, etc., alors le calcul suivant, où nous calculons successivement le reste de la division par deux puis divisons par deux nous donne… le codage binaire du nombre 9 :
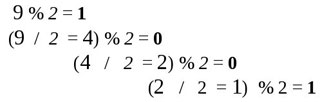
Représenter des entiers positifs de toutes tailles
Bien sûr, cela marche avec tous les nombres entiers positifs, et nous pouvons facilement calculer combien de bits sont nécessaires pour les coder :
| Entiers | 0 à 1 | 0 à 3 | 0 à 7 | 0 à 15 | 0 à 255 | 0 à 1023 | 0 à environ 4 milliards | 0 à plus de 1.8 x 10 20 |
| Codés sur | 1 bit | 2 bits | 3 bits | 4 bits | 8 bits | 10 bits | 32 bits | 64 bits |
Nos ordinateurs utilisent aujourd’hui souvent 32 ou 64 bits pour coder les nombres entiers, ils peuvent donc coder directement des nombres très grands et, si besoin était, en utilisant plus de bits… des nombres vertigineusement grands !
Calculer directement sur les nombres binaires
Nous pouvons donc représenter des nombres entiers positifs par la suite de bits de leur représentation binaire. Ce codage est très précieux, car il permet de faire directement des opérations sur ces nombres. Par exemple, additionner deux entiers positifs revient à additionner leur représentation binaire : on obtient directement le codage binaire du résultat. De même pour toutes les autres opérations numériques, pour comparer ces entiers entre eux, etc.
Souvenons-nous que toutes les valeurs numériques sont non seulement stockées en binaire, mais aussi
manipulées en binaire dans l’ordinateur.
Représenter des nombres entiers négatifs et positifs
Jusqu’ici, nous n’avons considéré que des nombres entiers positifs. Comment représenter des nombres entiers soit positifs, soit négatifs ? Eh bien, choisissons de représenter le signe par un bit supplémentaire :
| '0' | + |
| '1' | – |
Avec cet ajout, nous représentons la valeur absolue du nombre comme un entier positif, et son signe avec ce bit en plus.
Nous pouvons alors définir toutes les opérations numériques que nous connaissons en tenant compte de ce signe.
Représenter les nombres réels
Pour représenter un nombre réel, s’il s’agit d’un nombre décimal, par exemple 3.1416, nous utilisons la « notation scientifique » 31416 10-4, et codons d’une part l’exposant (ici -4) et d’autre part les décimales du nombre, plus exactement sa mantisse (ici 31416), sous forme de deux entiers, codés en binaire, et mis bout à bout.
C’est de cette façon que sont codés les nombres dans nos ordinateurs. Les calculs numériques se font alors directement sur les nombres binaires et sont ensuite transcrits pour afficher le résultat attendu.
Mais attention : les fractions comme 10/3 = 3.333333333 ... ou encore les nombres réels comme π = 3.1415926535897932384626433832795028841971…, ont une suite… infinie de décimales ! Cela veut dire que nous ne pouvons pas représenter leur valeur numérique, mais uniquement une approximation de cette valeur. De ce fait, tous les calculs que nous ferons avec un ordinateur ne seront jamais « justes » ! Ils ne seront pas vraiment « faux » non plus, ils seront approximatifs.
Et puis toutes les informations humaines…
Coder une mesure physique ?
Par exemple, comment coder la courbe de température de votre chambre au fil du jour ? On peut coder le nombre qui correspond à la mesure de température à chaque heure et les mettre bout à bout.
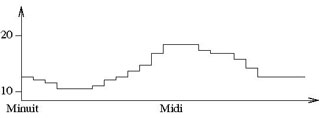
Ces 24 nombres vont donner une bonne approximation du chaud et froid, et du fait que… votre chauffage est visiblement coupé la nuit… brrrr. Ou alors, c’est que la température extérieure est beaucoup descendue, et que vous devez revoir votre isolation.
Coder un son ?
Le son peut être représenté par une courbe qui correspond aux vibrations de la voix, des bruits ou des instruments. Coder un son revient à coder une suite de valeurs numériques qui correspondent à cette courbe. Bien sûr, il faut beaucoup de valeurs : environ 10000 par seconde, pour obtenir une bonne approximation de toutes les vibrations sonores. Il faut 16 bits pour coder correctement la valeur de l’intensité et de la fréquence du son à chaque instant. Alors, pour coder une minute de son, il faut :
16 bits x 10000 valeurs/seconde x 60 secondes = presque 10 millions de bits.
C’est ce qui se passe dans les lecteurs MP3 par exemple, à une différence importante près. En effet, le codage de son avec le standard MP3 est « astucieux » : il met en œuvre des méthodes de compression avec perte qui tiennent compte de la perception humaine. Cette approximation supplémentaire permet de gagner de la place mémoire et du temps lors de la communication.
Coder de la musique ?
Il suffit de choisir un code binaire pour chaque note, sa hauteur (aigue ou grave) et sa durée, chaque instrument… Ensuite, en mettant bout à bout ces codes, nous obtenons la séquences des notes. On code ainsi la partition musicale et son interprétation. Un tel codage existe, il est standard et se nomme MIDI (Musical Instrument Digital Interface).
Coder un film ?
Un film n’est jamais qu’une séquence d’images ! Schématiquement, il suffit donc de coder les images et de mettre ces suites de bits bout à bout. Sans oublier de coder aussi le son. Là encore, il y a des astuces pour regrouper les parties qui se ressemblent et gagner de la place et du temps. Mais le principe reste le même.
Qu’avons-nous découvert ici ? La polyvalence des ordinateurs et des autres machines numériques :
ils traitent des données très diverses mais toujours décrites de la même manière par des suites binaires, utilisant deux symboles.
Mais au fait… pourquoi utiliser exactement deux symboles ?
Pourquoi utiliser un codage binaire ?
Il faut au moins deux symboles !
Pouvons nous utiliser moins de deux symboles pour décrire les images, les textes ou les nombres ? Non, car si nous avons un seul symbole, par exemple 0, une fois fixé le nombre de bits à 10, 100 ou 1 million, il n’y a qu’une seule suite de 10, 100 ou 1000000 symboles :
00000000000000000000000000…
qui ne peut donc décrire qu’un seul objet ! Et non servir à les décrire tous…
L’information commence avec la dualité — opposition et complémentarité — du 0 et du 1, du chaud et du froid, du bas et du haut… Quand on a un symbole unique, tout est uniforme. Et il n’y a pas d’information.
En utiliser deux, c’est bien pratique !
En revanche, nous aurions pu choisir d’utiliser plus de deux symboles : les dix chiffres arabes, les vingt-deux lettres de l’alphabet phénicien, les vingt-quatre lettres de l’alphabet grec ou les vingt-six lettres de l’alphabet latin…
Mais n’utiliser que deux symboles a plusieurs avantages. Le premier est que ce choix est indépendant de la nature des informations décrites. Il aurait été dommage de concevoir des ordinateurs grecs qui utilisent 24 symboles et des ordinateurs latins qui en utilisent 26.
Par ailleurs, la description de l’information avec deux symboles est plus simple à mettre en œuvre dans un ordinateur. Cela se réalise électriquement avec un interrupteur ouvert ou fermé, un courant électrique présent ou absent, etc. Ce choix rend aussi les ordinateurs plus robustes : s’il y avait plusieurs états intermédiaires au lieu de seulement deux, notés 0 et 1, le système physique pourrait plus facilement les mélanger, donc créer plus facilement des erreurs. En se limitant à 0 et 1, ce risque est minimisé.
Enfin, choisir deux valeurs électriques introduit un seul seuil de différenciation. Cela minimise donc les erreurs d’interprétation en cas de perturbation du signal.
Comme le signale justement Henri Gouraud, l’inventeur de la technique de rendu des images de synthèse 3D qui porte son nom : « C’est sans doute bien la qualité essentielle du code binaire que sa capacité à résister au « bruit » !
On pourrait en effet imaginer un autre code : 0 = absence de courant (0 volts), 1 = courant faible (6 volts), 2 = courant fort (12 volts), et définir ainsi un code ternaire (que les mathématiciens savent explorer et exploiter comme les autres bases de calcul).
Imaginez que l’alimentation de votre ordinateur ne sache délivrer un courant qu’avec une incertitude de plus ou moins 4 volts. Le codage binaire continuerait alors à fonctionner : 0 = entre -4 et +4 volts, 1 = entre +8 et +16 volts. Mais le codage ternaire ne fonctionnerait plus : 0 = entre -4 et +4 volts, 1 = entre +2 et +10 volts, 2 = entre +8 et +16 volts. Les plages d’incertitude se recoupent, d’où l’échec de ce codage devant ce niveau de bruit.
Or dans la nature, il y a toujours du bruit, et on cherche aussi toujours à utiliser le moins d’énergie (ou d’espace) possible (en réduisant le voltage à des niveaux qui peuvent être inférieurs à 12 volts). Dans ce contexte, le codage binaire est le plus robuste. »
Et cela permet aussi de mesurer la quantité d’information
Il y a une idée encore plus profonde ici. Le nombre de bits est exactement la quantité brute d’information qui a été codée.
Pour comprendre cette idée, jouons au jeu du portrait : devinez le nom d’une personne en ne posant que des questions où on répond par oui ou par non. Avec l’exemple ci-dessous :
| Qui ? | Genre ? | Look Emo ? | Moins de 15 ans ? | |
| Pierre | gars | oh non ! | oui | ‘001’ |
| Nadia | fille | good-good | oui | ‘111’ |
| David | gars | énormément | non | ‘010’ |
| Hamdi | gars | certes | oui | ‘011’ |
| Marie | fille | surtout pas | non | ‘100’ |
| Adèle | fille | évidemment | non | ‘110’ |
| MingYu | fille | beurk | oui | ‘101’ |
| Igor | gars | horreur ! | non | ‘000’ |
En trois questions :
« Est-ce une fille ? » « Aime-t-elle le look Emo ? » « A-t-elle moins de 15 ans ? »
vous allez forcément deviner parmi les huit personnes celle correspondant au portrait, car vous aurez toute l’information utile ici. D’ailleurs, nous avons symbolisé ce fait en utilisant un bit pour chacune des questions binaires, reporté dans la colonne de droite.
Deux questions binaires, c’est-à-dire deux bits d’information, ne suffisent pas ici. Par exemple, si vous ne savez pas si la personne recherchée a moins de 15 ans, alors Adèle et Nadia ou Igor et Pierre, par exemple, ne peuvent pas être distingués, puisqu’ils pensent la même chose du look Emo. On constate bien ici que le nombre de bits correspond au nombre de questions binaires à poser pour deviner toute l’information. Cela correspond donc à la taille en information.
Prenons un autre exemple : devinons l’âge d’un élève du secondaire, entre 11 et 18 ans. Nous pourrions poser 8 questions : « A-t-il 11 ans ? A-t-il 12 ans ? A-t-il 13 ans ? A-t-il 14 ans ? A-t-il 15 ans ? A-t-il 16 ans ? A-t-il 17 ans ? A-t-il 18 ans ? » avec le risque, si nous manquons de chance, de devoir poser les huit questions avant de connaître la solution.
Voici une meilleure méthode : demandons d’abord si l’élève a moins de 15 ans. Si la réponse est oui, alors nous savons que l’élève a entre 11 et 14 ans, si la réponse est non, alors nous savons que l’élève a entre 15 et 18 ans. Dans les deux cas, nous sommes passés d’une fourchette de 8 ans à une fourchette de 4 ans, nous avons divisé l’intervalle de recherche par deux, nous avons gagné un « atome » d’information, un bit d’information.
Si nous continuons à poser une question qui divise l’intervalle de recherche par deux, nous arrivons à une fourchette de deux ans, puis à la troisième question, à une fourchette d’un an… et nous avons trouvé la solution, l’âge de l’élève.
Nous voyons bien ici que ce choix parmi 8 valeurs correspond à 3 questions, donc 3 bits d’information,
chaque bit correspondant de gauche à droite aux réponses oui (= 1) ou non (= 0) aux trois questions :
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| ‘111’ | ‘110’ | ‘101’ | ‘100’ | ‘011’ | ‘010’ | ‘001’ | ‘000’ |
Ce qu’on peut appeler un « atome » d’information, c’est donc un bit, la réponse oui ou non à une question binaire, le choix entre deux options, etc.
La taille en information du choix entre plusieurs options correspond au nombre de bits pour le coder. Par exemple, choisir entre quatre couleurs : noir, rouge, vert, bleu nécessite deux bits.
Choisir entre les sept couleurs que nous voyons aujourd’hui dans l’arc en ciel nécessite trois bits :
| violet | indigo | bleu | vert | jaune | orange | rouge |
| ‘111’ | ‘110’ | ‘101’ | ‘100’ | ‘011’ | ‘010’ | ‘001’ |
tandis que le code ‘000’ n’est pas utilisé ici, ce qui importe peu.
La taille en information de deux informations indépendantes s’additionne. Par exemple, si nous codons l’âge d’un élève du secondaire sur 3 bits et son genre (fille/garçon) alors il faudra en tout 4 bits.
Mais la taille en information de deux informations redondantes ne s’additionne pas. Par exemple, si nous codons l’âge d’un élève du secondaire sur 3 bits et le fait qu’il ait le droit ou non de conduire un scooter sur 1 bit, puisque nous savons que toute personne de 14 ans et plus peut conduire un scooter, il est inutile d’ajouter cette information, car elle est « contenue » dans l’âge. Donc nous avons toujours 3 bits d’information.
Nous avons ainsi découvert une mesure physique très intéressante : de même que la chaleur se mesure avec la température en degrés, la tension électrique en volts, la quantité brute d’information se mesure en bits.
Cette mesure correspond tout simplement au nombre de bits minimum nécessaire pour stocker l’information sans la tronquer.
Évidemment, cette mesure ne dit rien de la valeur de l’information, ni de sa complexité. Par exemple, la séquence binaire :
1100100100001111110110101010001000100001011010001100001000110100
est constituée de 64 bits. A-t-elle un grande valeur ? Aucune, si les 0 et les 1 ont été choisis sans raison. A-t-elle une grande complexité ? (C’est-à-dire : est-elle difficile à calculer ?) Sûrement pas, si nous avons juste appuyé au petit bonheur la chance sur les 0 et 1 du clavier.
Mais voilà que cette séquence correspond au codage binaire au milliardième près du nombre le plus célèbre en mathématiques : le nombre π. Voilà qui le rend plus précieux et qui indique qu’il est plutôt complexe à calculer. Et pourtant, il est toujours constitué de 64 bits. C’est le contenu brut en information qui est mesuré ici, indépendamment de sa valeur ou de sa complexité.
Newsletter
Le responsable de ce traitement est Inria. En saisissant votre adresse mail, vous consentez à recevoir chaque mois une sélection d'articles et à ce que vos données soient collectées et stockées comme décrit dans notre politique de confidentialité
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Gilles Dowek
Chercheur Inria dans l'équipe Deducteam, jusqu'à son décès en juillet 2025.
Crédit Photo : Sébastien Dolidon.

Jean-Pierre Archambault
Ancien président de l'association Enseignement Public & Informatique (EPI), décédé en février 2025.

Benjamin Wack
Docteur en informatique, professeur de mathématiques à Villard-de-Lans.

