Non, les ordinateurs ne seront jamais tout-puissants !
Un algorithme énonce la résolution d’un problème bien posé sous la forme d’une série d’étapes de calcul à effectuer de manière à produire une sortie à chaque entrée soumise. Les étapes de calcul sont écrites dans un langage de programmation afin d’obtenir un programme informatique que l’on peut exécuter sur un ordinateur. On attend d’un algorithme qu’il résolve correctement un problème et que la sortie soit calculée en un temps raisonnable.
Un problème important est celui du tri de données pour lequel de nombreux algorithmes ont été développés. Nous présentons ici l’algorithme de tri par insertion. Les joueurs de cartes l’utilisent pour classer les cartes qui leur ont été distribuées. La main gauche tient les cartes déjà triées, tandis que la main droite insère chaque nouvelle carte reçue au bon endroit parmi les cartes de la main gauche (voir la séquence vidéo ci-dessous).

Démonstration du tri par insertion avec un jeu de cartes.
Visionner la vidéo – Durée : 36 s.
Cet algorithme de tri propose la série d’étapes de calcul suivante, une étape de calcul étant le placement d’une carte dans la main gauche, ou la comparaison d’une carte avec une autre :
Placer la première carte reçue dans la main gauche.
Pour chaque nouvelle carte c reçue
1. comparer cette carte c avec chaque carte de la main gauche jusqu’à repérer l’endroit où l’insérer.
2. placer la carte c à cet endroit.
Une majoration du temps nécessaire pour trier n cartes peut être estimée directement sur l’algorithme précédent sans devoir l’exécuter sur un ordinateur, en comptant le nombre d’étapes de calcul à effectuer, ici le nombre de comparaisons. La pire situation est celle où chaque nouvelle carte reçue doit être comparée à toutes les cartes de la main gauche. Ainsi, si la carte c est la ième reçue, il faut la comparer aux i-1 cartes de la main gauche avant de l’y placer, soit un total de i étapes de calcul.
Pour trier n cartes, le tri par insertion nécessite donc au pire de l’ordre de n2 étapes de calcul (précisément 1 + 2 + … + n = n × (n + 1) / 2 étapes). En considérant qu’une étape de calcul peut être exécutée sur un ordinateur en 1 nanoseconde (10-9 seconde) au plus, trier mille cartes prend de l’ordre de 0,001 seconde tandis que trier cent mille cartes prend de l’ordre de 10 secondes. Imaginons un autre algorithme de tri, appelé tri gourmand, demandant au pire un nombre d’étapes de calcul de l’ordre de 2n, au lieu de n2. Trier vingt cartes prendrait alors de l’ordre de 0,001 seconde tandis que trier cent cartes dépasserait … l’âge de l’univers ! En fait, les meilleurs algorithmes de tri connus ont une complexité de l’ordre de n log n, meilleure donc que n2, ainsi que le met en évidence la figure ci-dessous, représentant la croissance de n2, de n log n et de 2n en fonction de n.
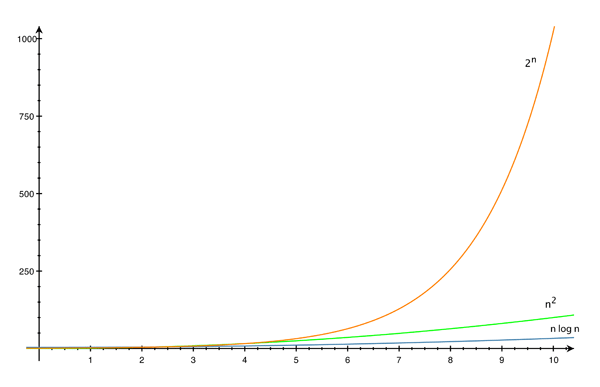
Croissance de n2, de n log n et de 2n.
De manière générale, la complexité d’un algorithme est le nombre d’étapes élémentaires de calcul nécessaires pour calculer la sortie à partir d’une entrée de taille n, dans la pire situation possible. Elle est souvent exprimée comme un ordre de grandeur en fonction de n. Les informaticiens estiment que les seuls algorithmes « raisonnables » sont les algorithmes polynomiaux, c’est-à-dire de complexité polynomiale, au plus de l’ordre nk pour un certain k (de préférence avec une valeur de k faible, typiquement inférieure à 4). C’est donc le cas pour l’algorithme de tri par insertion, mais pas pour l’algorithme de tri gourmand qui présente une complexité exponentielle, puisque n apparaît en exposant.
La classe P rassemble tous les problèmes pouvant être résolus par un algorithme polynomial. Pour certains problèmes, il s’avère difficile de trouver la solution, mais dès que celle-ci est fournie, il est facile de vérifier qu’elle résout bien le problème. Il suffit de penser à une grille de Sudoku qui, une fois remplie, peut être facilement vérifiée, alors qu’il est parfois diabolique de trouver comment compléter la grille. La classe NP rassemble tous les problèmes tels que si la solution est fournie, alors celle-ci peut être vérifiée comme étant correcte par un algorithme polynomial. La célèbre question P = NP ? a été posée par Stephen Cook en 1971, et à ce jour, aucun chercheur en informatique n’a pu y apporter de réponse. Un prix d’un million de dollars sera attribué à celui qui la résoudra. Tentons d’expliquer cette question. La question P = NP ? demande si les classes P et NP sont égales ou pas. Une réponse positive signifierait que vérifier l’exactitude d’une solution serait aussi facile que de calculer cette solution. Les chercheurs en informatique pensent que P ≠ NP, mais n’ont pu le démontrer à ce jour.
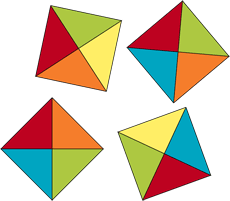
Puzzle de 4 pièces.
Présentons un problème simple de puzzle appartenant à la classe NP, mais pour lequel aucun algorithme polynomial n’est connu à ce jour. Commençons en considérant un puzzle de 4 pièces carrées, formées chacune de 4 triangles de couleur différente. Le but du puzzle est de placer ces pièces sur une grille carrée de taille 2×2 de telle sorte que les triangles qui se touchent soient de la même couleur. Un exemple de puzzle est donné sur la figure à droite. Nous invitons le lecteur à tenter de le résoudre (sans regarder la solution) pour qu’il puisse se rendre compte de sa difficulté.
Voici un exemple de configuration pour que les triangles se touchant soient de la même couleur.

Passons au cas général d’un puzzle de n2 pièces carrées à placer sur une grille de taille n×n. Ce problème appartient à la classe NP. En effet, si quelqu’un propose un placement des pièces sur la grille, on peut facilement s’assurer qu’il s’agit d’une solution du puzzle en comparant les couleurs des triangles qui se touchent. On peut se convaincre que 2n×(n-1) comparaisons de couleur sont nécessaires pour le vérifier. Cette tâche peut donc être effectuée par un algorithme polynomial.
Par contre, calculer une solution (plutôt que d’en vérifier une) s’avère être une tâche bien plus ardue. Montrons-le d’abord sur le puzzle de 4 pièces. Un algorithme naïf consiste à essayer tous les placements possibles des différentes pièces sur la grille. Afin d’évaluer la complexité de cet algorithme, comptons le nombre de possibilités. Nous avons 4 façons de placer la première pièce choisie sur la grille vide. Il reste ensuite 3 façons pour placer la seconde pièce, 2 pour la troisième pièce, et une seule pour la dernière pièce. A priori, nous avons donc 4×3×2×1 = 24 (noté 4!) possibilités pour remplir la grille. Mais attention, ce calcul ne tient pas compte des différentes rotations des pièces. En effet, une fois son emplacement choisi, une pièce peut y être placée de 4 façons différentes. Le nombre total de placements est donc de 24×44 = 6144. Dans le pire des cas, l’algorithme devra tous les essayer avant de trouver une solution au puzzle (obtenue par le dernier placement testé). Enfin, comme on l’a vu auparavant, vérifier qu’un placement est correct nécessite 4 comparaisons de couleurs de triangles. Ainsi dans la pire situation, l’algorithme naïf proposé effectue 6144×4 = 24576 étapes de calcul.
À ce jour, aucun algorithme polynomial permettant de résoudre ce problème de puzzle n’est connu. L’algorithme naïf présenté pour 4 pièces peut être généralisé au cas de N = n2 pièces, le nombre d’étapes de calcul étant alors égal à N!×4N×2n×(n-1) dans le pire des cas. Il s’agit d’un algorithme de complexité exponentielle. Pour mieux comprendre son comportement catastrophique, quelques exemples de temps d’exécution sont donnés sur le tableau ci-dessous (avec d’autres temps d’exécution donnés à titre de comparaison). Des algorithmes plus subtils ont été élaborés pour résoudre le problème de puzzle, mais aucun n’est polynomial. Ce problème est connu pour être parmi « les plus difficiles » de la classe NP ; on dit qu’il est NP-complet. Trouver un algorithme polynomial semble assez improbable au vu de la question « P=NP ? ».
| Algorithme naïf pour le puzzle 2 x 2 | 0,00002 sec. |
| Tri par insertion de 1000 cartes | 0,001 sec. |
| Tri gourmand de 20 cartes | 0,001 sec. |
| Tri par insertion de 100000 cartes | 10 sec. |
| Algorithme naïf pour le puzzle 3 x 3 | (1,1).103 sec. |
| Une journée (24 heures) | (8,6).104 sec. |
| Tri gourmand de 50 cartes | (1,1).106 sec. |
| Temps écoulé depuis la disparition des dinosaures | (8,5).1013 sec. |
| Algorithme naïf pour le puzzle 4 x 4 | (2,1).1015 sec. |
| Âge de l’univers | (1,9).1016 sec. |
| Tri gourmand de 100 cartes | (1,2).1021 sec. |
| Algorithme naïf pour le puzzle 5 x 5 | (6,9).1032 sec. |
Comparaison de temps d’exécution, sur la base d’un temps d’exécution d’une opération élémentaire en 1 nanoseconde. Tout l’intérêt des analyses de complexité est de caractériser les algorithmes sans avoir à se référer aux performances, variables, des ordinateurs.
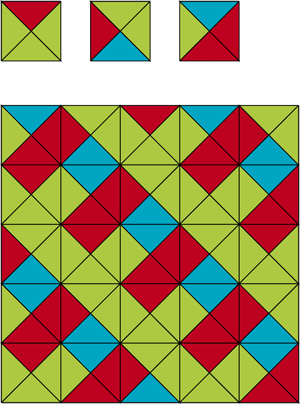
Envisageons maintenant une variante du problème de puzzle, appelée problème de pavage du plan. Ce problème diffère du problème de puzzle en trois points : le plan (infini) tout entier doit être recouvert plutôt qu’une grille (finie) ; on dispose d’un nombre fini de pièces, et d’une infinité de copies d’entre elles ; les pièces ne peuvent pas subir de rotation. Résoudre le problème de pavage du plan consiste à déterminer si, étant donné un nombre fini de pièces, il est possible ou non de recouvrir le plan tout entier. Un exemple de pièces avec lesquelles le pavage est possible est donné sur la figure de gauche, où seulement une portion finie du plan est pavée (mais cette portion va pouvoir s’étendre à l’infini). Un autre exemple pour lequel le pavage est impossible est donné sur la figure de droite.
 |
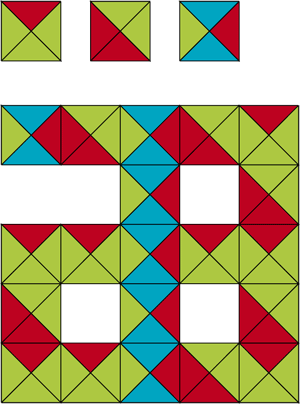 |
| Sur la figure de gauche, un pavage possible. À droite, un pavage impossible. | |
Ce problème est en fait bien plus compliqué que le problème de puzzle. En effet, on peut démontrer mathématiquement qu’il n’existe aucun algorithme qui, étant donné un ensemble de pièces, soit capable de résoudre le problème de pavage du plan, et ce quels que soient le temps et les ressources disponibles. Un tel problème est dit indécidable. L’indécidabilité est un autre concept fondamental de l’algorithmique, qui rend compte de l’inexistence d’algorithme pour résoudre une classe de problèmes, sans que la cause puisse en être une insuffisance technologique ou un manque de connaissance actuelle. Cette limite constitue une barrière théorique « infranchissable ». Ce type de résultat peut paraître surprenant, mais peut être rendu formel et tout à fait rigoureux grâce à la théorie de la calculabilité.
Beaucoup de mauvaises nouvelles ? Ce n’est pas tout à fait vrai… Revenons aux problèmes difficiles mais décidables, comme le problème de puzzle. Ceux-ci sont très nombreux et possèdent quantité d’applications concrètes. C’est le cas de beaucoup de problèmes d’optimisation, où l’on s’intéresse à rechercher une solution optimale parmi toutes les solutions possibles. Par exemple, étant donné n villes et les distances entre celles-ci, le problème du voyageur de commerce consiste à trouver un plus court chemin qui passe exactement une fois par chaque ville et revient à la ville de départ. Les domaines d’application sont nombreux, notamment dans les transports et en logistique. Une manière naïve de chercher à résoudre ce problème (NP-complet) est d’énumérer tous les chemins possibles et d’en repérer un plus court. Un petit calcul montre qu’il y a (n-1)!/2 différents chemins : avec 60 villes, cela représente plus de possibilités qu’il y a d’atomes dans l’univers (1080) !
Alors, comment aborder ce genre de problèmes en pratique ? Une idée est de se contenter d’une solution approchée (plutôt qu’optimale), mais pouvant être déterminée par un algorithme polynomial, et pour laquelle on a une certaine garantie de sa qualité. On parle d’algorithme d’approximation, avec la garantie exprimée comme un facteur d’éloignement de la solution approchée fournie par rapport à une solution optimale, dans le pire des cas. Pour le problème du voyageur de commerce, on possède un tel algorithme avec un facteur d’éloignement de 3/2. En d’autres termes, le chemin qu’il propose est au pire de longueur 50 % plus grande que le chemin le plus court. Pour de nombreux problèmes d’optimisation, on dispose d’algorithmes d’approximation avec de bons facteurs d’éloignement.
Pour conclure, les concepts théoriques de complexité algorithmique et de calculabilité permettent d’établir formellement les limites de l’informatique. Quand celles-ci rendent le prix de l’optimalité inabordable, les recherches peuvent se tourner vers des algorithmes d’approximation, afin d’obtenir de bonnes solutions en des temps très courts. Des chercheurs en informatique, notamment dans nos équipes à l’UMONS, poursuivent des travaux de recherche dans cette thématique, afin de classifier les problèmes étudiés en fonction de leur difficulté « algorithmique » et de proposer de « bonnes » solutions algorithmiques quand cela s’avère possible. De telles recherches théoriques constituent un premier pas vers le développement d’applications pratiques ou industrielles.
- G. Ausiello et al., Complexity and Approximation : Combinatorial Optimization Problems and Their Approximability Properties, Springer, 1999
- T. H. Cormen, C. E. Leiserson, R. L. Rivest, Introduction to Algorithms, McGraw Hill, 1997
- D. Harel, Computers Ltd, What they really can’t do, Oxford University Press, 2004
Une première version de ce document est parue dans le magazine « élément » de l’Université de Mons, n°05, en mars 2011.
Niveau de lecture
Aidez-nous à évaluer le niveau de lecture de ce document.
Votre choix a été pris en compte. Merci d'avoir estimé le niveau de ce document !

Thomas Brihaye

Véronique Bruyère

Hadrien Mélot